基于優化神經網絡的采集終端軟件可靠性預測
董永樂,毛永梅,張理放,張帆,白露薇,林海軍,梁肇聰
(1.內蒙古電力科學研究院,呼和浩特 010000; 2.哈爾濱理工大學,哈爾濱 150080 )
0 引 言
隨著智能電網建設在我國的深入開展,智能儀器、設備及綜合測量控制管理系統在電力系統中得到廣泛應用。由于智能電網對可靠性的要求非常高,所以對這些儀器、設備及系統的軟件、硬件的可靠性就提出了更高的要求。由于硬件集成度不斷提高,加之對硬件可靠性的研究投入大且成果比較豐富,相較于硬件,軟件可靠性的研究成為制約采集終端等儀器設備可靠性的關鍵問題,也是可靠性研究的焦點之一。智能電網是關系到國計民生的重要系統,電網數據采集終端作為智能電網的關鍵設備,其可靠性直接影響著智能電網自動化系統的可靠性,因此,以采集終端為切入點,開展軟件可靠性預測方法研究具有十分重要科學和現實意義。
從1967年Hudson提出了生滅過程模型開始,軟件可靠性預測模型研究受到關注,之后,學者們提出了幾十種軟件可靠性模型,如J-M 模型、MUSA執行時間模型及貝葉斯排錯模型等[1]。這些模型在一些分析軟件中得到應用,但由于假設前提高且各異,對同一軟件的評價結果迥異,影響了評價的公信力。
針對軟件可靠性預測,科研人員建立了多種模型[2-7]。研究證明,預測效果較好的是基于分類思想的模型[8]。支持向量機[9]及神經網絡理論[10-13]的研究成為熱點,用于軟件可靠性預測的神經網絡有BP神經網絡、LVQ神經網絡及小波神經網絡等[14]。但它們在應用中還是存在瑕疵。
例如,LVQ神經網絡神經元利用不充分及算法對初值敏感等;隱層節點數難定、收斂速度較慢、易陷入局部最優解等問題困擾著小波神經網絡,后兩個問題也同樣困擾著BP神經網絡。為此,研究者提出了一些解決方案,以期得到更好的識別效果,例如提出了采用改進遺傳算法AGA改進LVQ神經網絡,用粒子群算法優化模糊神經網絡等。
為了提高BP網絡收斂速度和全局尋優能力,提高軟件可靠性預測模型的預測能力,文章從完善SA和GA優化算法入手,給出改進的退火遺傳融合優化算法MSAGA,進而提出一種基于MSAGA-BP神經網絡的軟件可靠性預測模型,即利用BP神經網絡建立軟件可靠性預測模型,用MSAGA優化網絡參數,提高訓練速度、全局尋優能力和精度,最后,應用該方法對采集終端進行軟件可靠性預測模型建模分析,實現對該軟件可靠性的預測。
1 SAGFA-BP神經網絡
優化算法種類繁多,它們各有所長,各有所短,如果能取長補短則能收到更好的效果。在互補性分析,及完善算法的基礎上,文中將遺傳算法融合到退火算法中,提出退火遺傳融合算法,并用它解決BP神經網絡的優化問題。
1.1 GA的抗早熟改進
遺傳算法(GA)是模仿生物進化的優化算法。GA雖然理論上可以搜索到最優解,但受雜交算子的影響,也有可能陷入局部最優。研究表明,種群的多樣度高有助于全局搜索[15]。為了抗早熟,文中在判斷接受新個體時,把適應度和多樣度共同作為影響指標。
設種群Y用矩陣表示為:
(1)
若矩陣中非全1和非全0的列有m個,則Y的多樣度為:
μ(Y)=m
(2)
另外,對種群Y來說,其總體適應度Fs(Y)等于個體適應度的最大值。即:
(3)
文中對GA的新個體接受進行改進,其它流程不變。判斷接受時,先產生[0,1]上均勻分布隨機數α,然后以下式接受新一代個體:
(4)
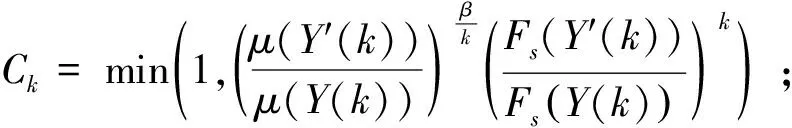
1.2 SA加速收斂方法
模擬退火(SA)算法是參考熱力學退火過程的優化算法。它全局尋優能力強,但耗時較長。為提高其效率,一方面,在確定初始溫度時,考慮最差的初始接受概率[16];另一方面,采取自尋優的方法[17]確定尺度。
為了防止初始溫度選擇得太高或者太低延緩SA收斂速度,選擇下式確定:
t0=(fmin-fmax)/lnpr
(5)
式中pr為最差概率;fmax和fmin分別為目標函數的極大值和極小值。
SA算法退火時,新狀態是通過在老狀態的基礎上,按照一定的尺度h隨機增加擾動實現的。方法如圖1所示。
x′(i)=x(i)+h·δ
(6)
1.3 融合優化算法SAGFA
針對GA和SA的優化質量和效率偏低的問題,文中提出退火遺傳融合優化算法(simulated annealing genetic fusion algorithm,SAGFA),該算法在上述算法改進的基礎上,通過互補融合,使新算法既具備GA的并行搜索能力,也兼具SA的概率突跳性,實現了高效與優質尋優的目標。SAGFA流程圖如圖2所示。
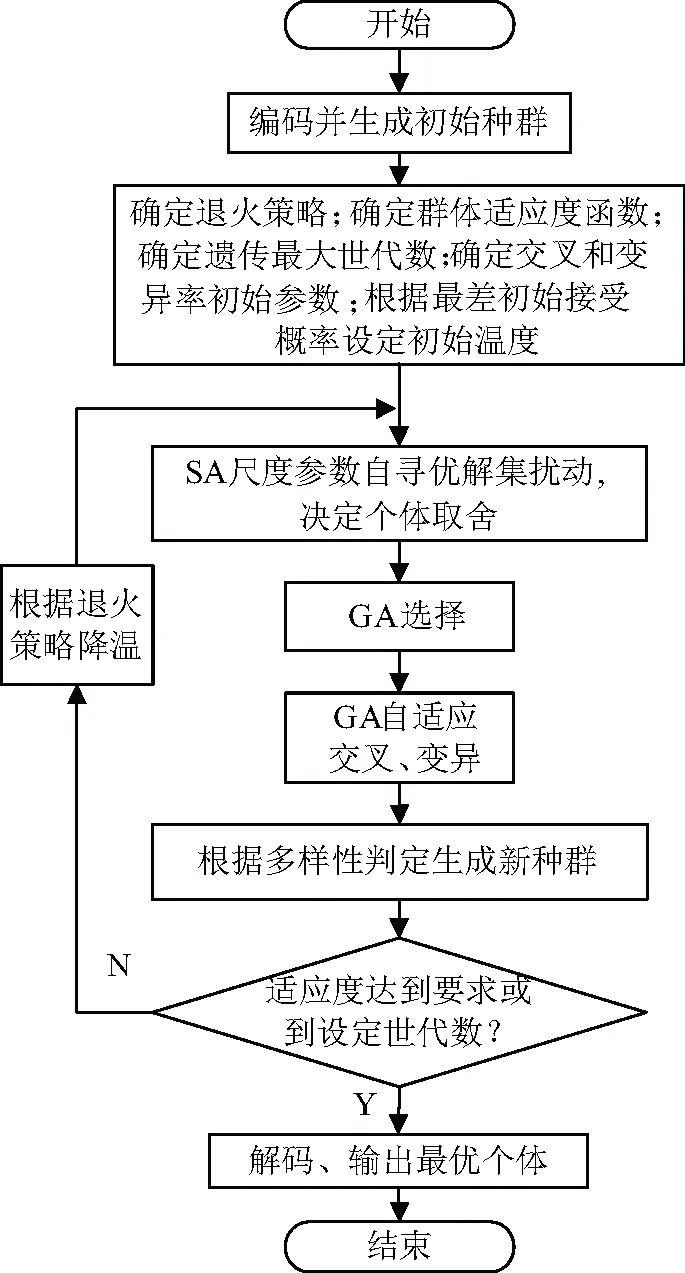
圖2 SAGFA算法流程圖
流程圖中需要說明的是:
1)選用適應度函數作為SAGFA的評價函數,尋優方向是增大;
2)初始溫度t0根據前面給出的式(5)確定;
3)采取指數下降策略;
4)按式(6)及圖1的流程進行擾動;
5)個體取舍時,若新狀態的適應度變大,則接收新狀態,否定依據Metropolis準則,按概率接收新個體;
6)交叉時,為了保護優秀個體,依據下式自適應調節交叉率:
(7)
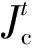
文中利用普遍使用的有代表性的6個標準函數[18]的極值搜索進行仿真,分別用SA、GA和SAGFA三種算法對6個函數搜索極小值,取搜索到全局最優解(最優解絕對誤差小于10-5即認為搜索成功)20次的平均搜索時間(單位:s)列于表1。
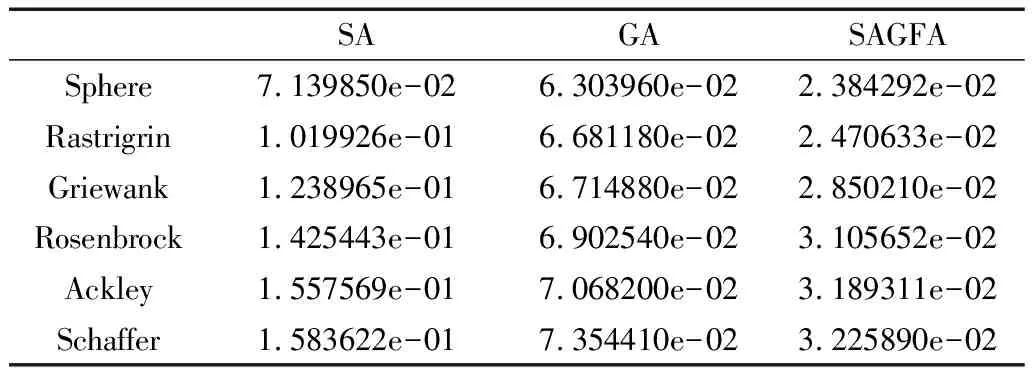
表1 三種算法仿真結果
仿真結果表明:在同樣搜索到全局最優的情況下,SAGFA較遺傳算法和模擬退火算法具有更好的搜索速度。
1.4 SAGFA-BP神經網絡
如前所述,多種神經網絡各有不足。BP神經網絡是誤差反傳神經網絡(back propagation neural network,縮寫為BPNN)。相對而言,BPNN具有非線性映射能力強、結構簡單、泛化能力強、激活函數輸入空間不受限且理論上可全局尋優等優點,因此,文章以它為基礎,采用SAGFA改善其尋優速度和精度,以達到更好的預測效果。BPNN基本結構如圖3所示。
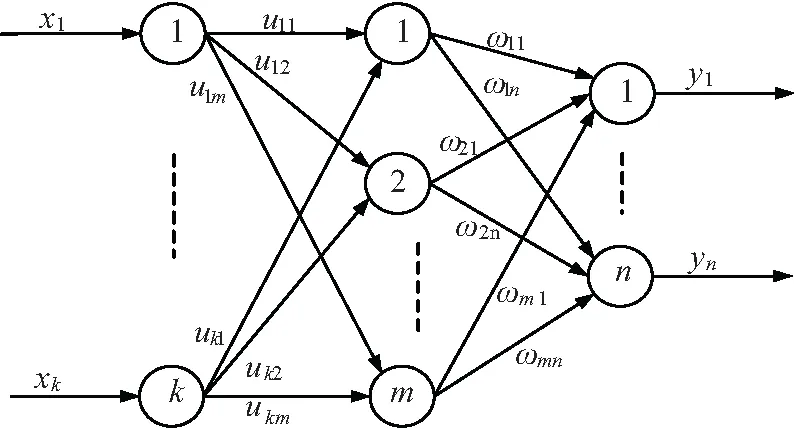
圖3 BPNN原理框圖
理論研究表明,所有非線性函數都可以采用單隱含層的前饋網絡來映射,所以,文中的BPNN采用輸入層、單隱含層和輸出層的三層結構,每層由若干個節點(即神經元)組成,同層神經元之間無任何聯系。其中網絡節點的激活函數很重要,通常選用標準Sigmoid函數,可全局尋優。節點輸出函數表達式為:
(8)
式中xi為神經元輸入;y為神經元輸出;θ為閾值;ωi為連接權值。
BPNN雖然具有上述優點,但也存在訓練收斂有平緩區、高精度的訓練完成時間較長的不足。訓練的實質就是根據輸入和輸出的目標值,優化神經網絡連接權值,使實際輸出按照訓練精度要求趨近目標值的過程,若能快速地找到全局最優的權值組合,就可一舉克服上述不足。因此,文章采用SAGFA優化連接權值,提出SAGFA-BPNN網絡。
SAGFA-BPNN采用SAGFA對BPNN參數進行優化,是將BPNN的各層間的連接權值進行編碼,并按照一定的規則構成染色體,用與BPNN的辨識誤差成反比例的適當函數作為適應度函數,利用SAGFA搜索到最優解。這些最優解的染色體編碼,根據前述的規則解碼,就得到了BP神經網絡的最優化的各層間的連接權值。SAGFA-BPNN原理框圖如圖4所示。
從圖4可以看出,SAGFA的染色體編碼由BP神經網絡的連接權值按照一定的順序組成。圖中給出的網絡輸入節點為k個,隱含層節點為m個,輸出節點為n個,這樣,染色體中的u11,…,ukm為輸入層k個節點到隱含層的m個節點的連接權值,ω11,…,ωmn分別為隱含層m個節點到輸出層n個節點的連接權值。
SAGFA的優化結果中染色體的不同位作為BP神經網絡的不同支路的連接權值,由于SAGFA優化算法得到最優解,對應著適應度函數取得極大值,而對于BP神經網絡則應該達到最小的辨識誤差。因此,SAGFA算法的適應度函數為與辨識誤差函數成反比例的函數,我們取適應度函數為:
g=1/(1+E)
(9)
式中g為適應度函數;E為BP神經網絡訓練的系統辨識誤差。
2 基于PCA及SAGFA-BPNN的軟件可靠性建模
2.1 實驗數據的PCA處理
若實驗數據維數太多,不僅會增加用于可靠性預測的神經網絡的輸入節點數,而且會增加樣本噪聲,影響預測的準確率,因此,維數太多時需要進行降維處理。
降維的方法較多[19],可以采取成分分析類的方法,如獨立成分、主成分等,也可以采取回歸分析類的方法,如逐步、多元、階躍函數、樣條及多項式等。由于主成分分析(PCA)可消除指標間的相關影響,且降維效果較好,所以,文中運用PCA進行數據處理,剔除影響模型準確率的冗余和干擾樣本。
設原始數據矩陣為:
(10)
式中n為樣本數,k為樣本因數維數。
歸一化后,將X的k個變量線性合成為m(k≥m)個新變量,如下:
(11)
1)yi與yj(i≠j;i,j=1,2,…,m)不相關;
2)y1為具有最大方差的線性組合;
3)y2滿足第(1)條,亦為方差最大者;
4)y3~ym依此類推,依順序確定。
新變量y1,y2,…,ym分別稱為原變量中第1個、第2個、…、第m個主成分。第1個主成分y1的方差貢獻率最大,依次遞減。
文中建立可靠性模型時可適當選擇前幾個主成分,使方差的累積貢獻率超過85%即可。
2.2 基于SAGFA-BPNN的軟件可靠性建模
基于SAGFA-BPNN建立軟件可靠性預測模型的主要步驟如下所示,流程圖如圖5所示。
以往模式中很難對業主的責任進行集中化劃分,不能明確地指出。對于EPC工程的總承包模式來說,雖然一直是五方主體的責任不發生變化,總承包的企業還是需要承擔總體責任,一旦工程涉及到勘測和設計與采購以及施工的問題,那么總承包就要承擔一定的責任。在傳統模式的基礎上,設計施工的過程中會發生扯皮問題,EPC模式基礎上的問題扯皮是在總承包的范圍中出現的,必須要總承包進行內部把控以及管理,因此,對于總包管理制度和核心能力與人員專業提出較高的要求。如果不能很好地把控,所產生的風險就要由總包單位進行負責。此時,就需要分包和分包以及分包和主體施工之間協調管理有效地對接,一旦出現疏忽,勢必會造成索賠。
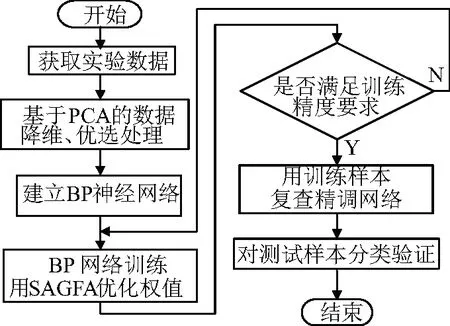
圖5 建立軟件可靠性預測模型的流程
1)進行軟件測試,獲得多維度的多次實驗數據;
2)采用PCA降低維數、優化數據,減少神經網絡輸入節點數,以便于提高預測精度;
3)建立BP神經網絡,確定輸入、輸出及隱含層的節點數;
4)輸入訓練樣本數據,利用SAGFA優化BP神經網絡的連接權值;
5)用訓練樣本數據復查精調神經網絡完成全部網絡訓練。
將測試樣本輸入到訓練好的SAGFA-BPNN進行分類預測,并輸出結果。
3 采集終端軟件可靠性預測建模實驗
3.1 采集終端軟件組成及可靠性分析
采集終端軟件平臺基于ARM平臺和嵌入式操作系統,采用模塊化設計,軟件功能結構如圖6所示。系統軟件可以分為操作系統層和業務應用層,其中操作系統層就有約20項功能,業務應用層也有7項以上應用程序,還可以根據需要可以拓展軟件功能。可見,采集終端軟件系統是由很多個功能模塊,或者說子系統組合而成,子系統間相互作用,相互協調完成系統功能。
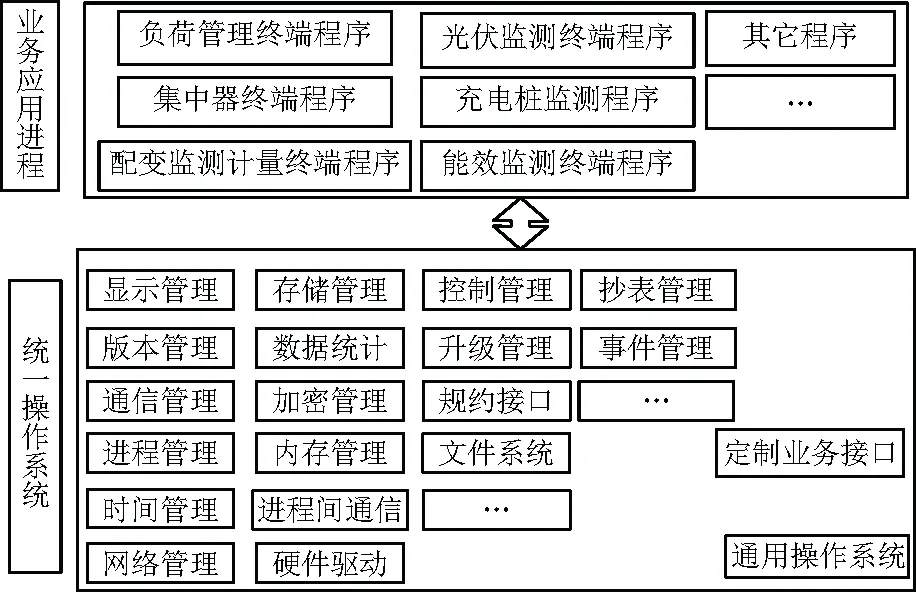
圖6 采集終端軟件功能結構圖
根據軟件子系統的相對獨立性,以及它們之間相互的調用情況可知,整個軟件的系統故障率等于各子系統故障率與其調用系數乘積的累加[20],即:
(12)
式中πi為子系統Xi(i=1,2,…,n)的調用系數。
在可靠性預測實踐中,πi值可采用子系統Xi的運行時間占整個系統運行時間的比例來表示。系統的可靠性函數為:
(13)
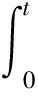
可見,系統的可靠性可以通過求解各個子系統的故障率來求得。
考慮到采集終端軟件的復雜性,其可靠性分析可以通過軟件的功能模塊分解及可靠性建模來實現。
3.2 實驗數據
采集終端基于ARM平臺和嵌入式系統,由于嵌入式系統的獨特性,其測試需要專用的測試工具,主流測試方法可分為靜態分析法、動態測試法和綜合測試法三類。采用可靠性增長測試階段的綜合性測試法所獲得的部分數據進行研究。為節省篇幅,數據采用圖7的曲線呈現。
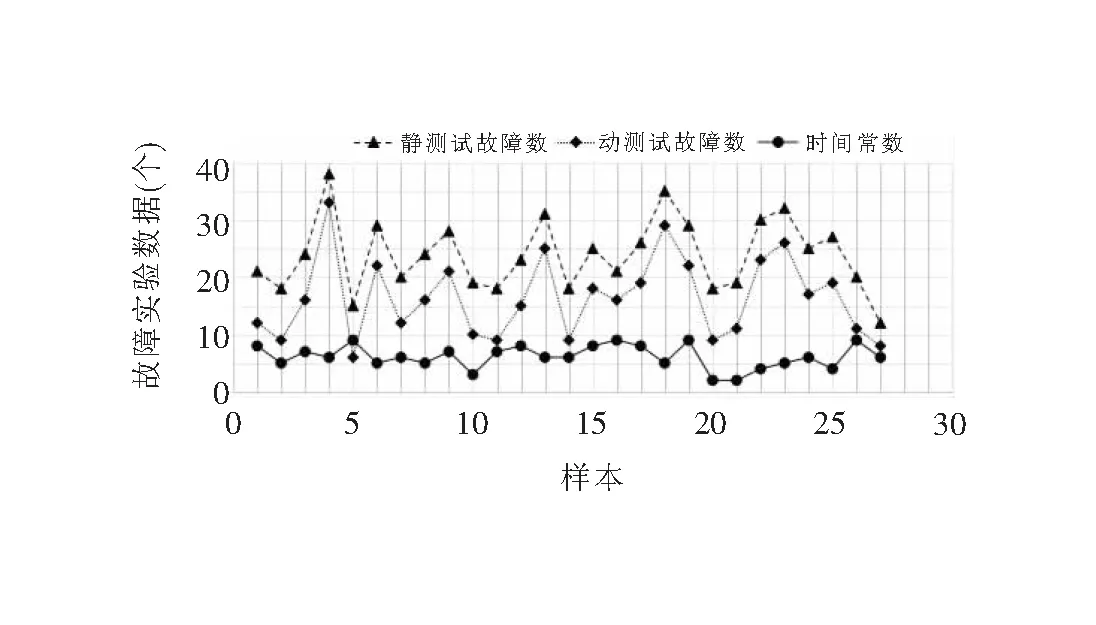
圖7 實驗數據曲線
3.3 軟件可靠性預測建模實驗結果與分析
基于前面的研究結果,采用PCA降維、去噪,得到的主成分輸入到SAGFA-BPNN中進行可靠性預測建模的實驗方法。
建模實驗采用MATLAB仿真軟件進行。為了觀察PCA的效果,以及主成分貢獻率對預測結果的影響,文章選擇不同的保留率進行仿真實驗。
SAGFA-BPNN的訓練精度如果設置的太高則可能造成過訓練,降低泛化能力,設置的太低則影響預測的準確率,因此,為了兼顧泛化能力和預測準確率,訓練的均方誤差設置為1%。
預測目標值Rti依據式(13)計算得到,神經網絡的輸出為預測值Ri,則預測的絕對誤差為:
δi=|Ri-Rti|
(14)
式中δi為第i個樣本的預測絕對誤差;Rti為第i組數據的目標值;Ri為第i組數據的預測值。
實驗采用18組樣本作為訓練樣本,另外的9組樣本作為檢驗樣本。不同貢獻率的軟件可靠性預測結果如圖8所示,預測的絕對誤差如圖9所示。可以看出:第一,對每組數據都能較準確地預測出可靠性;第二,模擬保留率為90%的曲線與保留率100%的曲線相比,前者的模擬效果略微好于后者,這說明采用PCA進行數據預處理,不僅可以降低維度,還可以在一定程度上去除冗余信息及減小噪聲干擾,更有利于預測,噪聲信息越多,這種現象越明顯;第三,從誤差的曲線來看,所有點的絕對誤差都在0.07以內,平均誤差更低,這是由于訓練的均方誤差設置為1%的結果,若有需要,可通過提高訓練指標以減小絕對誤差;第四,所建立的軟件可靠性模型具有很強的泛化能力,對檢驗樣本的識別準確性也非常好。實驗證明,文中提出的可靠性建模方法可行,完全滿足軟件可靠性預測建模的要求。
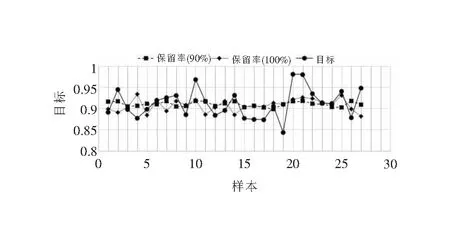
圖8 不同貢獻率的軟件可靠性預測結果
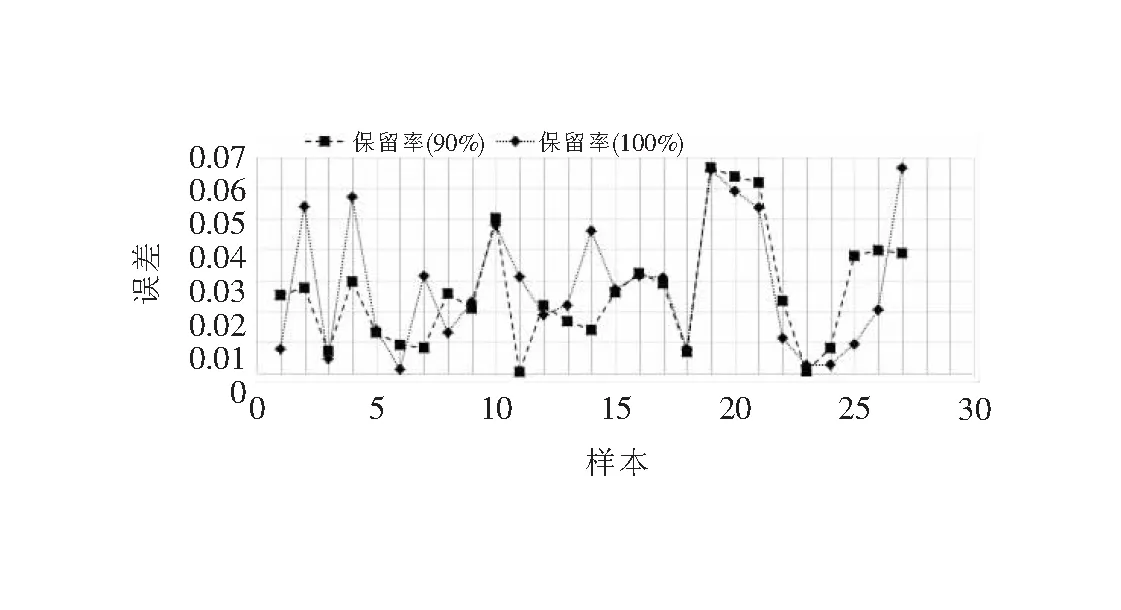
圖9 不同貢獻率的預測誤差曲線
4 結束語
針對軟件可靠性預測問題,在創建優化算法并提出SAGFA-BPNN的基礎上,進一步提出了基于PCA和SAGFA-BPNN的軟件可靠性預測模型建模方法,并成功應用于采集終端軟件可靠性預測建模。該方法克服了以往的基于多種神經網絡的軟件可靠性建模存在的收斂速度慢、針對存在冗余和噪聲數據的情況預測準確率低的難題。仿真及實驗結果表明,SAGFA-BPNN訓練收斂快、全局尋優能力強,所建立的軟件可靠性模型具有很強的泛化能力,訓練速度及預測效果優于典型神經網絡的預測模型。文章方法具有重要的參考價值。

