基于流固耦合的攪拌磨磨礦離散元仿真及試驗研究

劉 偉 劉 俊 程 波 薛玉君,4 李濟順,4

(1.河南科技大學機電工程學院,河南 洛陽 471003;2.河南省機械設計及傳動系統重點實驗室,河南 洛陽 471039;3.洛陽礦山機械工程設計研究院有限責任公司,河南 洛陽 471039;4.智能礦山重型裝備全國重點實驗室,河南 洛陽 471039)

立式螺旋攪拌磨是一種超細磨設備,常應用于精礦再磨和尾礦再磨工藝,其能量利用率高,產品粒度細,最小可將礦石研磨至10 μm以下,且結構簡單,占地面積小,對建設綠色礦山具有重要意義[1],因此,對立式螺旋攪拌磨進行磨礦過程仿真分析也愈發重要。而研磨介質作為磨礦設備的重要組成部分,如何在降低成本的同時,又能達到較好的磨礦效果一直以來都是選礦工作者的難題,選擇合適的研磨介質對磨礦本身具有重大意義[2]。近年來,離散單元法逐漸興起,該方法通過建立固體顆粒體系的參數化模型,進行顆粒的行為模擬和分析,被廣泛應用于散狀物料和粉體工程領域[3]。但是,立式螺旋攪拌磨在實際工況下采用濕法研磨的方法,筒體內部呈多相流混合狀態,在螺旋攪拌器的作用下,礦物和研磨介質做自轉和螺旋上升運動,通過研磨介質的沖擊、擠壓和摩擦對物料進行研磨來實現礦石的粉碎。單獨采用離散單元法并不能夠對立式螺旋攪拌磨的磨礦過程進行準確模擬,而采用流固耦合的方法進行仿真分析能夠更準確地分析其在實際工況下的磨礦特征。

國內外學者利用流固耦合方法對立式螺旋攪拌磨的磨礦機理及研磨行為展開了大量研究。STROBEL等[4]以小型攪拌磨機為研究對象,分析了介質球尺寸和流體黏度對物料應力狀態的影響,結果表明,較大的磨粒可得到較高的應力能,而黏度的增加會降低應力能。PRZIWARA等[5]研究了在攪拌磨機中助磨劑對磨粒穩定性的影響,結果表明,磨機內部礦漿的流動行為會對磨礦效果產生較大的影響。盧世杰等[6]建立了立式螺旋攪拌磨的CFD單相流仿真模型,分析了不同轉速和不同螺旋直徑對立磨機內流場速度的影響,結果表明,轉速或螺旋直徑增大時,流場速度呈增大趨勢。孫新明等[7-8]采用流固耦合的方法建立了立式螺旋攪拌磨仿真模型,得出了螺旋攪拌器運行的阻力矩,同時,還進行了螺旋攪拌器結構強度分析,為磨機的設計和制造提供了依據。孫小旭等[9-10]建立了超細磨用攪拌裝置流體力學仿真模型,得到了攪拌裝置的流場分布狀態和輸入功率變化情況,為實驗和工業中超細磨技術和設備的研發奠定了基礎。

研磨介質的尺寸和形狀會對立式螺旋攪拌磨的磨礦效果產生很大的影響,采用CFD-DEM(Computational Fluid Dynamics-Discrete Element Method)的方法建立礦漿與研磨介質的流固耦合模型,探究立式螺旋攪拌磨在采用不同尺寸和形狀的研磨介質時的磨礦特征,并結合立式螺旋攪拌試驗磨機的磨礦試驗結果,分析研磨介質的尺寸和形狀與磨礦效果的關系,為立式螺旋攪拌磨的研磨介質選型提供依據。

1 流固耦合模型的建立

1.1 流體連續相控制方程

以立式螺旋攪拌磨內部礦漿為對象建立流體模型,由于礦漿處于恒溫恒壓下,且考慮到其與研磨介質的相互影響,在守恒方程中加入一個額外的體積分數項[11],由流體力學守恒理論可知,其守恒方程有:

質量守恒方程:

式中,εl為空隙率,ρl為礦漿密度,kg/m3;t為時間,s;ul為礦漿流速,m/s。

動量守恒方程:

式中,gl為礦漿重力加速度,m/s2;μl為礦漿動力黏度,Pa·s;S為動量匯,由以下公式算得:

式中,FD為研磨介質所受礦漿作用力的總和,N;V為控制體的體積,m3;n表示控制體內研磨介質的數量。

1.2 顆粒離散相控制方程

以研磨介質為對象建立離散元模型,根據牛頓第二定律可推導其平衡方程[12]為

式中,mp為研磨介質質量,kg;up為研磨介質速度,m/s;Fg為研磨介質自身的重力,N;Fd為研磨介質所受的曳力,N;Fb為浮力,N;Fc為研磨介質之間以及研磨介質與壁面之間的接觸力,N。

曳力模型選擇Wen Yu & Ergun模型[13],其計算公式可表示為

式中,Vp為研磨介質體積,m3;uf為研磨介質與礦漿的相對流速,m/s。

β由下式計算獲得:

式中,L為研磨介質粒徑,m;CD為曳力系數,由以下公式算得:

式中,Re為雷諾數,由以下公式算得:

除了曳力,還需考慮礦漿對研磨介質產生的浮力,浮力計算公式如下:

研磨介質之間、研磨介質與壁面之間的接觸模型選擇Hertz-Mindlin(no-slip)模型[11],其計算公式如下:

法向接觸力Fn及法向阻尼力Fdn:

式中,E?為等效彈性模量,Pa;R?為等效半徑,m;δn為法向重疊量,m;m?為等效質量,kg;為相對速度的法向分量,m/s;e為恢復系數,Sn為法向剛度,N/m;由以下公式算得:

切向接觸力Ft及切向阻尼力:

式中,δt為切向重疊量,m;為相對速度的切向分量,m/s;St為切向剛度,N/m;由以下公式算得:

式中,G?為等效剪切模量,Pa。

滾動摩擦力Fr由以下公式算得:

式中,η為摩擦系數,Ri為研磨介質質心到接觸點的距離,m;ωi為研磨介質接觸點的角速度,rad/s。

2 磨機模型的建立

2.1 三維模型及網格劃分

立式螺旋攪拌試驗磨機的結構非常復雜,在建模過程中需要對其進行一定的簡化。試驗所采用的物料為赤鐵礦,密度為3 900 kg/m3,入料粒度為-1 mm,研磨介質的直徑一般為8～10 mm,兩者直徑相差很大,仿真無法準確模擬出赤鐵礦的破碎過程。因此,將赤鐵礦與水混合的礦漿簡化成一種單一的流體[14],默認磨機內部只存在礦漿和研磨介質兩種物質,將筒體及攪拌器視為無厚度的壁面。由于在FLUENT中要通過滑移網格來實現攪拌器的旋轉運動,因此,需要對立式螺旋攪拌磨的流體域劃分旋轉域和靜止域,旋轉域為主動旋轉運動區域,靜止域由旋轉域帶動其進行旋轉運動。圖1和表1分別為立式螺旋攪拌試驗磨機部分結構參數及三維模型。

表1 立式螺旋攪拌試驗磨機結構參數Table 1 Structural parameters of vertical spiral stirring test millmm

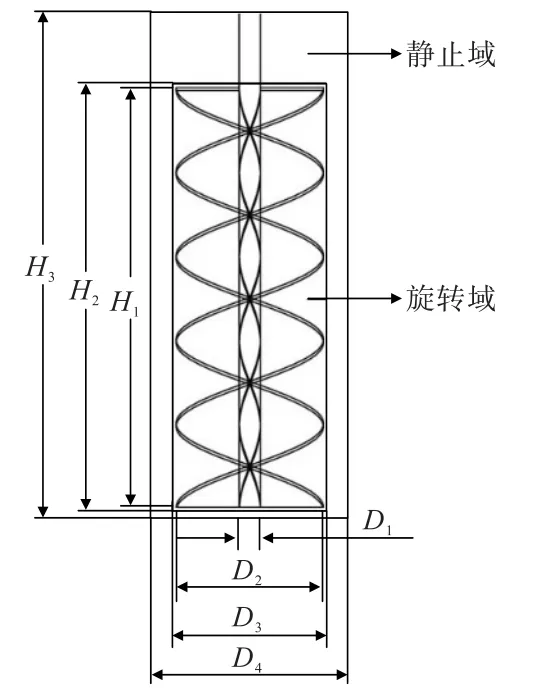
圖1 立式螺旋攪拌試驗磨機三維模型Fig.1 3D Model of vertical spiral stirring test mill

在DESIGN MODEL中進行流體域抽取,利用FLUENT MESHING對模型進行網格劃分,靜止域網格最大尺寸控制為20 mm,旋轉域網格最大尺寸控制為15 mm,對靠近攪拌器的網格再進行適當加密,網格類型選擇多面體網格。經過質量提升、節點移動,最終得到如圖2所示的網格,網格數量為4.75萬個,最小正交質量為0.36。將旋轉域和靜止域的交界面定義為interface,用于數據交換。

圖2 立式螺旋攪拌試驗磨機網格剖視圖Fig.2 Section view of mesh of vertical spiral stirring test mill

2.2 耦合模型設置

在FLUENT中輸出邊界網格,將邊界網格導入到EDEM中。在EDEM中對研磨介質進行預填充,預填充時攪拌器不進行旋轉運動,以保證與FLUENT耦合時網格初始狀態相同,EDEM時間步長選為0.000 001 s,點擊Start Coupling Server,使EDEM處于耦合接聽狀態。

在FLUENT中選擇瞬態求解方式,導入耦合接口UDF。在FLUENT與EDEM的耦合中,能夠實現固體與流體雙向耦合的模型有兩種:Lagrangian模型和Eulerian模型。Lagrangian模型只考慮固體和流體之間的動量交換,FLUENT采用單相流計算,一般情況下,該模型只適用于稀相流,即顆粒相體積分數小于10%,且顆粒之間沒有相互作用。Eulerian模型除了考慮固體和流體之間的動量交換外,在FLUENT中還需開啟歐拉多相流模型,利用顆粒位置、體積等計算顆粒在網格內體積分數。在立式螺旋攪拌磨中,研磨介質在磨機內部呈堆積形態,礦漿與介質、介質與介質之間都會發生相互作用,因此,采用Eulerian模型進行耦合。曳力模型選擇Wen Yu & Ergun模型,連接成功后FLUENT會自動打開歐拉多相流,設置兩種歐拉相,主相為流體相,次相為離散相。湍流模型選擇k-epsilon-RNG模型,標準壁面函數。

FLUENT轉速與EDEM相同,出口設置為壓力出口,時間步長為EDEM時間步長的100倍,即0.000 1 s。由于FLUENT在仿真開始時引入顆粒會對內流場湍流引起較大變化,極易引起仿真發散,因此,須將體積分數項松弛因子調小,在FLUENT內流場穩定后再逐漸調大。

在仿真中,通過改變密度和黏度來控制礦漿的濃度,礦漿密度ρl由以下公式算得:

式中,C為礦漿質量濃度,%;ρw為水的密度,kg/m3;ρm為干礦密度,kg/m3。

礦漿的動力黏度μl由Einstein黏度公式可得,即

式中,μw為水的動力黏度,Pa·s;φ為礦漿體積濃度。

但是,該公式未考慮顆粒相互作用的影響,僅適用于顆粒濃度較低的稀相流,因此,根據CHENG等[15]提出的指數模型對該公式進行一定的擴展:

本研究使用?8 mm鋼球、?12 mm鋼球和?8 mm×10 mm鋼段作為研磨介質,3種研磨介質所使用的均為同一種鋼,其材料屬性如表2所示。磨機運行參數如表3所示。

表2 研磨介質材料屬性Table 2 Material attributes of grinding media

表3 磨機運行參數Table 3 Operating parameters of the mill

3 仿真結果分析

3.1 磨機內部壓力及研磨介質速度

圖3、圖4為磨機內部壓力云圖和研磨介質速度云圖,可以看到,隨著攪拌器的轉動,顆粒會向葉片邊緣運動,葉片中心顆粒較少,其速度最小,壓力也最小;而葉片邊緣由于需要推動顆粒運動,因此此處的速度最大,壓力也最大;在筒壁處,雖然此處的顆粒密集,但由于受攪拌器運動影響較小,所以此處的壓力雖大,但速度卻很小。

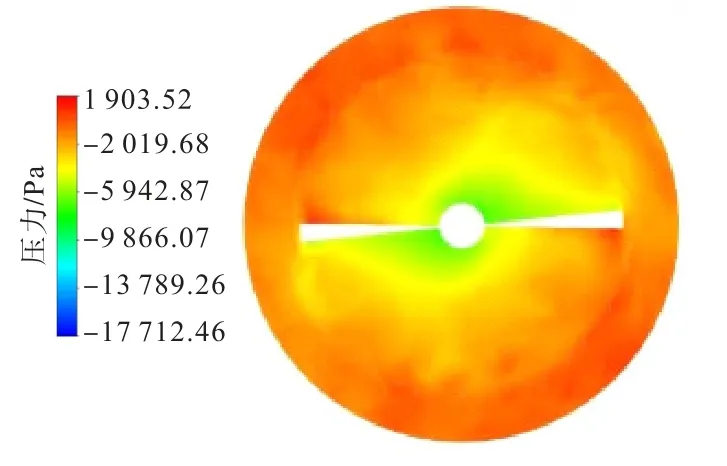
圖3 磨機內部壓力云圖Fig.3 Pressure cloud inside the mill

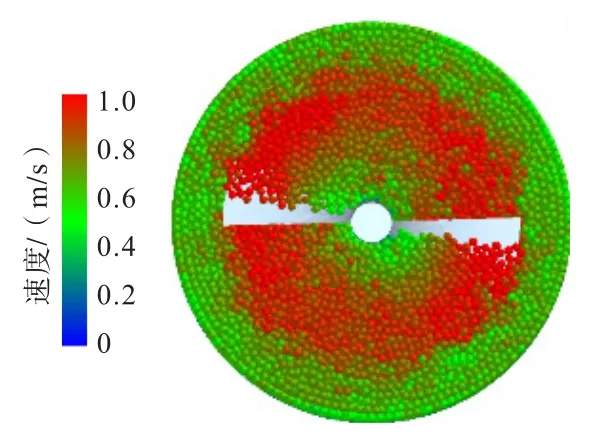
圖4 研磨介質速度云圖Fig.4 Speed cloud of grinding media

3.2 攪拌器扭矩

圖5～圖7為填充研磨介質尺寸為?8 mm鋼球、?12 mm鋼球以及?8 mm×10 mm鋼段時提取的攪拌器扭矩,可以看到,在啟動研磨時,攪拌器扭矩會急劇增大,然后逐漸下降至在一定范圍內波動。對穩定后的扭矩求取平均值,可得使用?8 mm鋼球時攪拌器平均扭矩為83.19 Nm、使用?12 mm鋼球時攪拌器平均扭矩為92.95 Nm、使用?8 mm×10 mm鋼段時攪拌器平均扭矩為104.1 Nm。大球比小球所產生的扭矩要大,鋼段比鋼球所產生的扭矩要大。隨著扭矩的增大,立式螺旋攪拌磨的能耗也會增大,故使用?8 mm鋼球作為研磨介質時磨機的能耗最小。

圖5 ?8 mm鋼球時攪拌器扭矩Fig.5 Torque of the mixer when ?8 mm steel balls

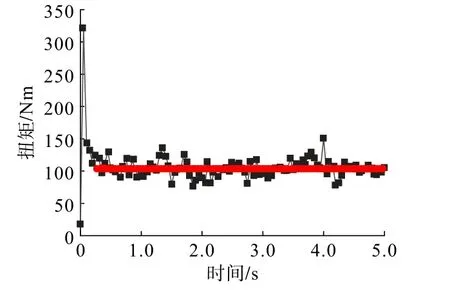
圖7 ?8 mm×10 mm鋼段時攪拌器扭矩Fig.7 Torque of the mixer when ?8 mm×10 mm steel segments

3.3 磨礦效果

由于仿真中將礦漿簡化成一種單一的流體,無法檢測其出料粒度,因此,仿真的磨礦效果可以通過分析研磨介質的運動速度、碰撞次數以及碰撞力來間接評價。

3.3.1 研磨介質運動速度

待磨機運行穩定后,截取距磨機底部五分之一高的平面,分析該平面內的研磨介質的運動速度。以攪拌器中心為原點,提取距原點不同徑向距離處的研磨介質平均運動速度,結果如圖8所示。

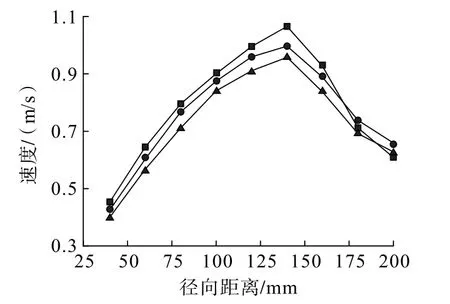
圖8 不同徑向距離處的介質速度Fig.8 Speed of different radial distance grinding media

從圖8可以看出,隨著距原點徑向距離的增加,研磨介質的運動速度先提高后降低,在攪拌器邊緣處達到最大值,且?8 mm鋼球的速度最大,其次是?12 mm鋼球,?8 mm×10 mm鋼段的速度最小。在攪拌器邊緣距桶壁的環形區域內,由于研磨介質不被攪拌器的旋轉所帶動,因此,其運動速度隨著徑向距離的增加而減小。在桶壁處,?8 mm鋼球的速度反而降到最小,這是由于在同一徑向距離區間內,?8 mm鋼球的數量是最多的,速度的傳遞次數增多,因此桶壁邊緣處的速度也就要小得多。

3.3.2 研磨介質碰撞次數

提取3種研磨介質的顆粒數量以及在2 s內的總碰撞次數,結果如圖9所示,可以看到,?8 mm鋼球的數量最多,總碰撞次數也最多,其次是?8 mm×10 mm鋼段,而?12 mm鋼球的數量最少,總碰撞次數也就最少。

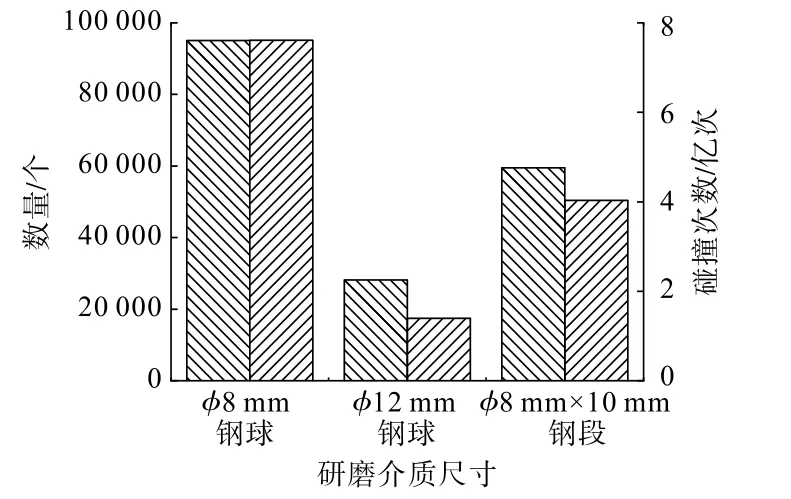
圖9 研磨介質數量及碰撞次數Fig.9 Quantity of grinding media and number of collisions

3.3.3 研磨介質碰撞力

提取3種研磨介質在不同時間點產生的平均法向力和平均切向力,結果如圖10、圖11所示。可以看到,由于?12 mm鋼球的質量相比其他研磨介質來說要大很多,因此,該介質之間所產生的碰撞力也最大,其次是?8 mm鋼球,?8 mm×10 mm鋼段之間所產生的碰撞力最小。

圖10 不同研磨介質的平均法向力Fig.10 Average normal force of different grinding media

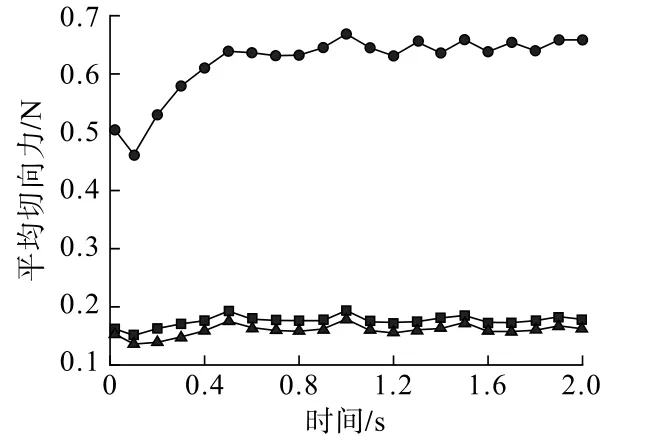
圖11 不同研磨介質的平均切向力Fig.11 Average tangential force of different grinding media

結合研磨介質運動速度、碰撞次數及碰撞力來分析,?12 mm鋼球的碰撞力雖然比?8 mm鋼球要大,但是其數量以及碰撞次數要小很多,而且速度也沒有?8 mm鋼球的速度大,這就導致?12 mm鋼球對物料產生的沖擊、剪切以及摩擦次數要少得多,所以?8 mm鋼球的磨礦效果要比?12 mm鋼球的好。而相比?8 mm×10 mm鋼段來說,?8 mm鋼球無論從運動速度、碰撞次數和碰撞力都要比其大,因此,?8 mm鋼球的磨礦效果也要比?8 mm×10 mm鋼段的好。

4 立式螺旋攪拌磨試驗

在立式螺旋攪拌試驗磨機上,以赤鐵礦的原礦石為物料,分別使用?8 mm鋼球、?12 mm鋼球以及?8 mm×10 mm鋼段進行試驗,試驗參數與仿真參數保持一致,使用KRT扭矩轉速傳感器檢測攪拌器的扭矩,1次加料28 kg,分時取樣進行分析。分別檢測使用3種研磨介質時的攪拌器平均扭矩,以及在研磨1 h后的篩下累積粒度,結果如表4和圖12所示。

表4 試驗測得扭矩Table 4 Torque measured by the test

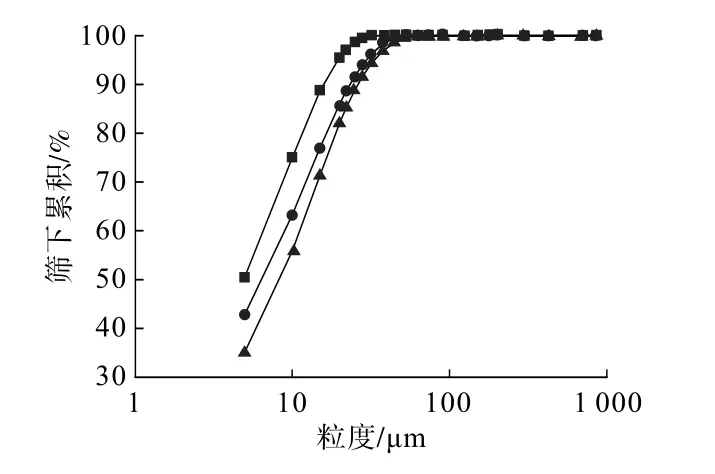
圖12 不同粒度的篩下累積量Fig.12 The accumulation under sieve of different particle sizes

將仿真所求得的平均扭矩與實驗中檢測出的扭矩平均值進行對比,可以看到,仿真所提取的攪拌器扭矩與實驗所測得的扭矩數值基本一致,誤差在5%以內,且使用?8 mm鋼球時的扭矩最小,其對應的能耗也就最低。

從實驗數據來看,使用?8 mm鋼球作為研磨介質時,粒度為5 μm的物料顆粒篩下累積量最多,能夠達到50.51%,當使用?12 mm鋼球時,此粒度的篩下累積量為42.83%,當使用?8 mm×10 mm鋼段時,僅僅為35.1%。可以看到,使用這3種研磨介質時的磨礦效果差距還是較大的,?8 mm鋼球的磨礦效果最好,?8 mm×10 mm鋼段的磨礦效果最差,這與仿真結果也是可以相互對應的。

5 結 論

(1)利用CFD-DEM的方法建立了立式螺旋攪拌試驗磨機的流固耦合模型,分析了在使用不同尺寸和形狀的研磨介質時的磨礦特征。隨著距離攪拌器中心徑向距離的增加,研磨介質的速度呈先增大后減小的趨勢。在攪拌器邊緣處,研磨介質的速度達到最大值,是對物料粉碎最有效的區域。

(2)?12 mm鋼球產生的碰撞力雖然較大,但其數量過少,碰撞次數相比其他兩種介質要少很多,對礦漿產生的有效研磨很少。而?8 mm鋼球的運動速度和碰撞次數在3種介質中最大,能夠對礦漿產生更多的有效研磨次數,更有利于礦物粉碎,因此,使用?8 mm鋼球的磨礦效果要優于其他兩種介質。

(3)利用立式螺旋攪拌試驗磨機進行了赤鐵礦石磨礦試驗,結果表明,鋼球直徑越小,攪拌器的扭矩越小,磨機能耗也越小,達到出料標準的物料篩下累積量越多,且使用鋼球介質比鋼段介質的物料篩下累積量多。說明使用小鋼球的磨礦效果好能耗低,這也與仿真結果相對應。