面向醫療數據的隱私保護聯邦學習架構
王 波,李洪濤,王 潔,郭一娜
(1.太原科技大學 電子與信息工程學院,山西 太原 030024;2.山西師范大學 數學與計算機科學學院,山西 太原 030039)
1 引 言
隨著人工智能、大數據、物聯網等前沿技術應用于醫療行業,大量醫療數據隨之生成[1]。對醫療數據進行分析、挖掘可以促進醫療行業的發展和革新。例如,借助機器學習算法對醫療數據進行挖掘、分析,可以提高模式的分析能力、非結構化數據的分析、預測能力和可追溯性,輔助醫療決策[2]。然而,這些數據通常包括患者的身份信息、患病信息、社會關系等敏感數據,一旦被惡意攻擊者竊取或操控,將會嚴重危害患者的安全。近年來,醫療數據的隱私泄露問題引起了廣泛的倫理以及法律關注。因此,探索醫療數據的隱私保護策略具有重要的現實意義[3-4]。
出于數據安全和隱私的考慮,不同醫療機構之間存在數據屏障,無法實現數據的安全共享[5]。此外,各機構獨立的訓練模型無法達到全局優化。針對以上問題,谷歌提出了一種去中心化的分布式機器學習框架——聯邦學習(Federated Learning,FL)[6],將原始數據保留在節點上進行本地訓練,訓練好的模型上傳給中央服務器,服務器聚合模型后再下發給各節點,從而將數據共享問題轉化為模型共享問題,這使得一些敏感數據能夠在“不出域”的情況參與訓練,很大程度解決了隱私泄露問題。通過聯邦學習,將各個醫療機構的“數據孤島”聯合起來協同訓練的全局模型精度更高、泛化性更強[7]。然而,聯邦學習過程中仍存在隱私泄露的風險:半誠實或惡意的參與方加入訓練極易導致隱私泄露[8];惡意攻擊者可以從共享模型參數中反推出參與者的部分敏感信息[9];服務器端返回的全局模型中會攜帶一些規律信息,攻擊者可以推測出訓練集參與方或訓練集原始樣本,且全局模型也可能是一個已經被投毒者“篡改”的模型,其學習模型不僅準確率低且會泄露用戶的隱私[10]。
針對以上問題,文中旨在解決醫療數據在聯邦學習中的以下3個挑戰:首先,根據醫療數據的分布特征,選擇合適的機器學習模型提高訓練模型精度;其次,如何在保證數據高可用性的前提下增強數據的隱私保護力度;最后,如何在隱私保護技術產生的額外通信開銷和聯邦通信效率中取得平衡。
因此,文中基于同態加密技術提出了一種面向醫療數據的聯邦學習隱私保護架構(Homomorphic Encryption Federated Learning for Privacy-preserving and Security,HEFLPS)。在模型性能、隱私保護和通信效率之間取得平衡,更適用于醫療數據場景。主要貢獻如下:
(1) 提高了模型的訓練精度。文中搭建了卷積神經網絡(Convolutional Neural Network,CNN)模型,在新型冠狀病毒(Corona Virus Disease 2019,COVID-19)數據集和MNIST手寫數字數據集上均表現出較好的性能。
(2) 增強了聯邦學習的安全性和隱私性。在模型共享階段,采用同態加密技術對用戶共享的訓練模型進行加密,可以在不損失模型訓練精度的情況下確保共享模型的安全性和隱私性。
(3) 降低了惡意客戶端加入訓練的可能性。結合Schnorr零知識證明(Zero-Knowledge Proof,ZKP)身份認證構建了身份認證模塊,確保了參與訓練的客戶端身份的真實可信性。
(4) 彌補了同態加密帶來的時間開銷大的弱點。采用消息確認(ACKnowledgement,ACK)機制將離線或無響應用戶暫時剔除,解決了用戶在訓練過程中退出的問題,提高了通信效率,縮短了等待同步聚合的等待時間。
2 相關工作
醫療數據共享是各個醫療機構間合作的基礎,但其涉及到的隱私問題也是阻礙機構間數據共享的主要因素之一[11]。因此,解決聯邦學習中信息泄露問題十分必要。相關的研究方法主要分為兩類:一種是加密技術,包括安全多方計算[12](Homomorphic Encryption,HE)[13]和同態加密(Secure Mul-tiparty Computation,MPC);另一種是在模型參數中加入噪聲,如差分隱私(Differential Privacy,DP)[14]。
FANG等[15]采用安全多方計算提出了一種在云計算中具有強大隱私保護作用的高效聯邦學習架構,通過設計有效的優化策略提高學習效率,并表明該方案對于“誠實且好奇”以及“相互勾結”的服務器是安全的。但安全多方計算存在“信任問題”和“通信量問題”,同態加密則可以較好地解決上述問題。于是,KU等[16]將同態加密應用在由物聯網設備收集的醫療數據隱私泄漏問題中。數據加密上傳到霧節點,霧節點與云服務器協作完成模型的訓練,提高了方案的魯棒性,并解決了加密數據計算成本和存儲成本高的問題。此外,JIANG等[17]提出了一種基于混合差分隱私和自適應梯度壓縮的聯邦學習框架,更適應于工業環境中的邊緣計算,有效防止隱私數據受到推理攻擊的威脅。
然而,差分隱私技術需要在數據或模型參數中添加隨機噪聲來實現隱私保護,將會導致訓練的模型不夠準確,最終導致訓練精度不高[18]。相比之下,加密機制借助多方安全計算、同態加密等技術能夠在提供隱私保護的同時保持模型的準確性,適用于參與方少、對準確性要求較高的場景。然而,密碼學技術會造成協同訓練效率低、存儲和時間開銷大等問題,且對參與方是否在線要求較高[19]。
由此可見,聯邦學習系統所采用的隱私保護技術各有優劣,需要根據具體的應用場景選擇適當的技術設計高效、實用的隱私保護方案。文中針對醫療數據的特殊性,設計了一種新的聯邦學習架構,實現了隱私保護、模型性能和通信效率之間的平衡。
3 背景知識
3.1 聯邦學習


(1)
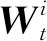
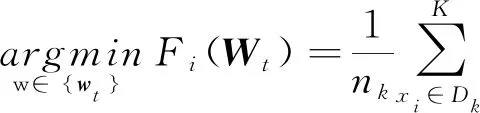
(2)
其中,nk表示客戶端數量。
3.2 Paillier同態加密
同態加密是指對明文進行環上的加法和乘法運算再加密,與加密后對密文進行相應的運算,結果是等價的[21]。Pallier同態加密是一種滿足加法同態的部分同態加密方法[22],由密鑰生成、加密和解密3個階段組成。
(1) 生成密鑰。 令公鑰為(n,g),對應的私鑰為(λ,μ),有
λ=lcm(p-1,q-1) ,
(3)
μ=(L(gλmodn2))-1modn,
(4)
其中,n為公鑰長度;g的階是n的倍數;p和q為兩個素數,滿足gcd(pq,(p-1)(q-1))=1;lcm代表最小公倍數;L(x)=(x-1)/n。
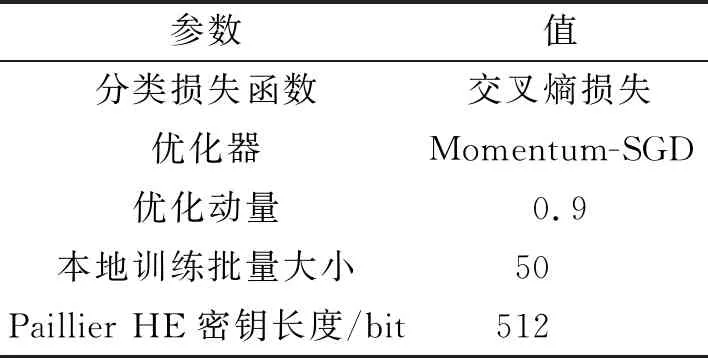
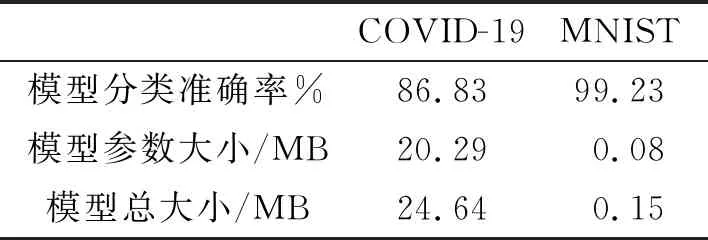
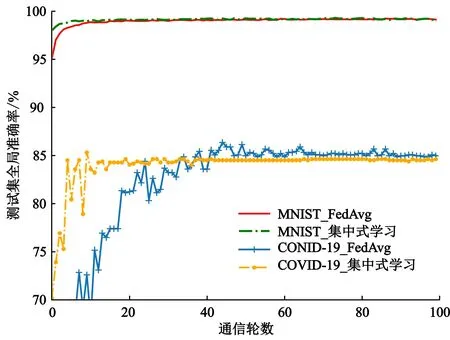
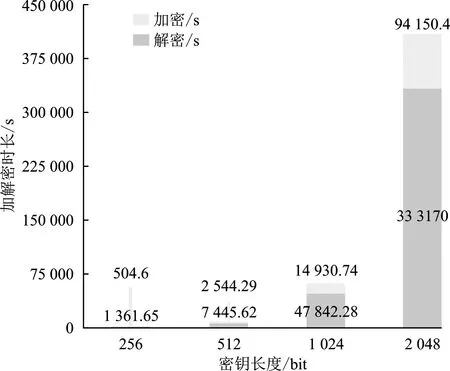
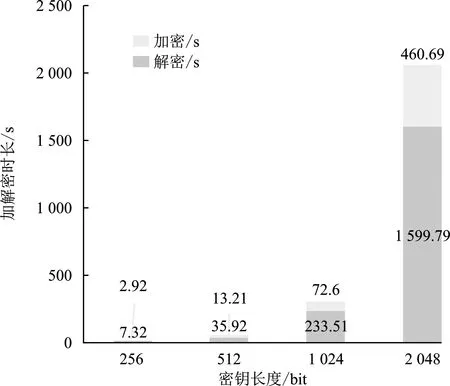
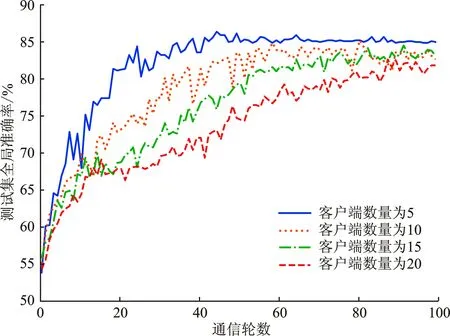
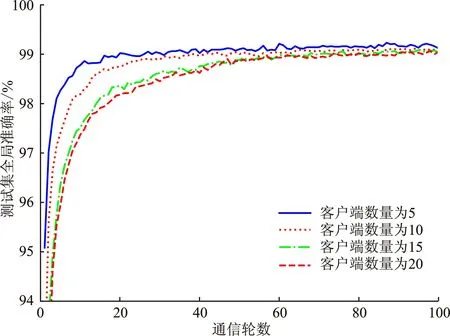
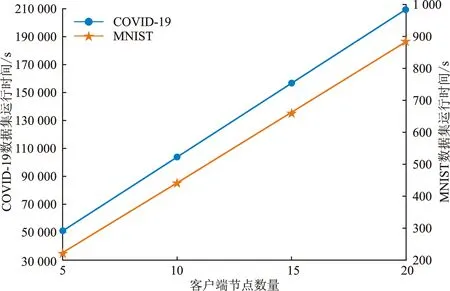
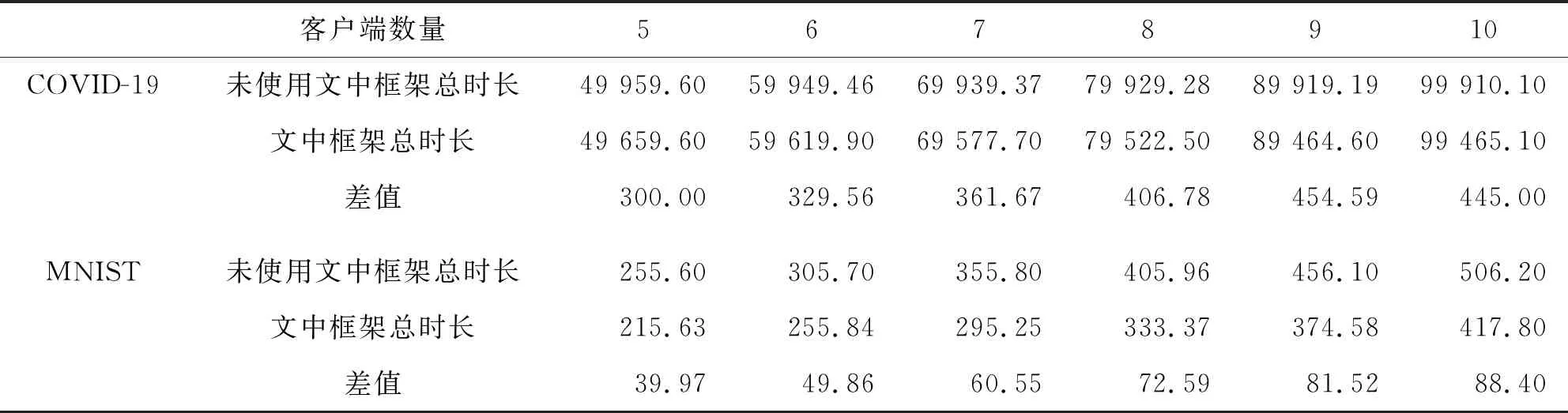
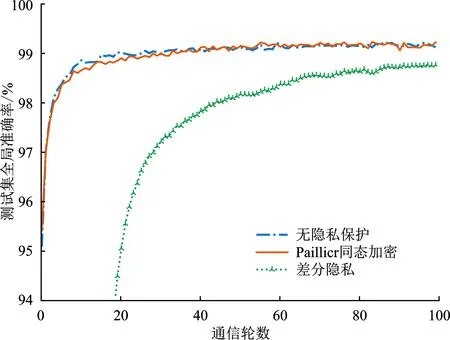
(2) 加密。 令密文和明文分別為c c=(gmrn)modn2。 (5) (3) 解密。 私鑰的解密過程為 m=L(cλmodn2)μmodn。 (6) 文中基于Pallier同態加密技術提出了一種高效的聯邦學習隱私保護方案,系統架構如圖1所示。采用同態加密技術對中間參數進行加密處理,提高了模型的安全性和隱私性;利用Schnorr零知識身份認證技術對客戶端進行身份認證,確保了用戶身份的真實性;使用消息確認(ACK)機制使服務器端對參與用戶進行離線監測,并及時刪除離線用戶,減少了通信等待時延。總體算法偽代碼如算法1所示。 圖1 HEFLPS系統結構圖 HEFLPS主要執行步驟如下: (1) 客戶端選擇。 中央服務器將通過身份認證的用戶Ck設定為參與本輪訓練的客戶端。 (2) 廣播。 服務器端通過消息確認機制剔除離線用戶并篩選下一輪參與訓練的用戶Cnew。 重復以上步驟,直到迭代t輪停止。 算法1HEFLPS算法描述。 輸入:客戶端集合C={c1,c2,…,ck},本地數據集D={di} 服務器端: 初始化 從通過身份認證的用戶kclients?C中隨機選擇一些參與訓練 ① 循環 ④ if用戶cm返回ACK,則加入C中組成一個新的用戶集合Cnew={cm1,cm2,…,cmk} ⑤ else認為用戶離線,不參與本次訓練 ⑥ 循環結束 客戶端: ⑦ pk,sk← 生成Paillier密鑰對(一次一密) ⑧ 循環 ⑨ 更新本地模型Wi+1←Wi-η?fi 4.2.1 模型參數加密 聯邦學習在模型傳輸過程中,模型參數會暴露給中心服務器,中心服務器下發的全局模型參數也會被每個客戶端獲取。攻擊者可以發起重建攻擊(Reconstruction Attacks)[23],通過共享的參數反向推斷出原始數據,獲取用戶的隱私信息。針對該問題,文中基于Pallier同態加密技術提出了保護隱私的聯邦學習架構,對中間過程交互的模型參數進行加密,從而實現模型參數的隱私保護。但Paillier同態加密只能實現密態加法運算,若出現乘法運算,文中則通過泰勒展開[24]將乘法運算以多項式相加的形式替換后,再進行同態加運算。 設有xi個數據,傳輸的加密模型參數為[W],對數損失函數可以表示為 (7) 對于任意的函數f(θ),在θ=0處的泰勒展開式為 (8) 當f(θ)為對數損失函數,即f(θ)=log(1+exp(-θ)),在θ=0處的泰勒展開表達式為 (9) 文中使用二階多項式來近似對數損失函數,將θ=[W]Tx代入上式,并代入式(9),得到: (10) 對上式求導,得到損失函數關于參數[W]的加密梯度值為 (11) 4.2.2 Schnorr零知識身份認證 如果惡意攻擊者獲得用戶的公鑰,并對數據進行解密后添加隨機擾動噪聲,將導致計算無意義或使服務器無法分辨接收到的結果正確與否。因此,驗證客戶端身份的真實性也十分必要。 傳統的認證機制包括兩個實體,即用戶和服務器。服務器擁有所有用戶的身份信息,因此很容易獲得用戶的信息。同時,用戶發送給服務器用來身份驗證的簽名信息也可能被攻擊者截獲,從而計算出用戶的身份信息,造成用戶的信息泄露。文中提出的基于Schnorr零知識的身份認證機制則可以較好地解決以上問題。其中零知識證明[25]是指證明者能夠在不向驗證者提供任何有用信息的情況下,使驗證者相信某個論斷是正確的。Schnorr機制[26]是一種基于離散對數難題的零知識證明機制。文中的認證模塊中,客戶端C需向服務器端S證明自己擁有對身份信息的數字簽名(h,x),而不泄漏有關h和x的任何有用信息以證明身份的真實性。公共參數:p為任意素數,生成元為g,公鑰為v=g-s(modp)C,擁有的私鑰為s。其認證過程如圖2 所示,具體描述如下。 圖2 Schnorr零知識身份認證過程 (2) 服務器端S驗證。 計算R′=gxvh(modp),并驗證h=Hash(R′,M),如果相等,則身份驗證通過;否則,不通過。 驗證過程為證明h=Hash(R′,M)。首先,證明R′=R。將v代入R′中,得 R′=gxg-sh(modp)=gx-sh(modp) , (12) 又因為x=r+hs,得r=x-hs,代入式(1),得R′=gr(modp),故R′=R。 在客戶端,同態加密的加密和解密時間以及模型的訓練時間是一次迭代時長的主要組成,其中,20%的時間用于數據傳輸和等待模型參數聚合返回[27]。在得到來自中央服務器返回的全局模型之前,任何客戶端均無法進行下一次迭代。 在服務器端,由于同步障礙,參與訓練的客戶端之間的資源和數據異質性可能會導致客戶端不同的響應延遲,這通常被稱為掉隊者問題(Straggler Problem)[28]。設客戶端Ci的響應延遲為Rt,則服務器的等待延遲為 Rt=max(R1,R2,…,R|C|) 。 (13) 從式(13)可知,在每一輪訓練中,服務器的等待時延為客戶端中最大的響應時延,即由最慢的客戶端決定,需等待其完成訓練后才能進行聚合更新,這是造成通信效率低的主要原因之一。 為了解決服務器端無效的通信等待時延問題,文中對響應時間過長和離線的用戶分別進行處理,如算法2所示。 挑選客戶端的規則:設第t輪更新中所挑選的活躍客戶端集合為C={c1,c2,…,ck},每個客戶被選中的概率設為1/τ。 中央服務器S對集合C中每個用戶發送確認消息,如果接收到用戶的ACK,則將該用戶添加到Cnew中;否則,認為該用戶離線不參與本輪更新(離線用戶仍可參加下一輪迭代)。在Cnew中,將響應時間最長的用戶被選中的概率降為其原來概率的1/k,Pτ可表示為 (14) 算法2服務器端異步聚合。 輸入:客戶集C={c1,c2,…,ck} 輸出:更新客戶集C′new 初始化 隨機選擇用戶kclients?C ① 循環 ② 通信輪數t ③ 廣播 ④ ifcm用戶返回ACK ⑤ 更新的用戶集Cnew={cm1,cm2,…,cmk} ⑥ 標記返回ACK最長時間的用戶T_Max(Cnew) ⑦ 減少該用戶下一次參與訓練的概率為(1/k)T_Max(Cnew) ⑧ else if ⑩ end if 對HEFLPS的安全性分析如下: (1) 同態加密隱私保護機制。首先,聯邦學習通過將數據保留在本地的形式進行訓練學習,避免了數據暴露給第三方,保證了數據的安全性和隱私性;其次,客戶端向服務器端發送的是加密后的模型參數,由于Paillier同態加密方案滿足CPA安全性,即使攻擊者截獲了加密后的模型參數,也無法獲取到明文數據,實現了“原始數據不出域,數據可用不可見”。 (2) 客戶端身份認證。不誠實或惡意的客戶端可能會共享無效數據或有害數據,文中通過Schnorr零知識身份認證技術確保只有合法的客戶端才能參與訓練。假設C沒有私鑰sk,那么C很難構造一個簽名(h,x)以通過S的驗證。由于哈希函數和離散對數的困難性,S也很難根據(h,x)反推出C的私鑰。 (3) 誠實且好奇的服務器。由于客戶端上傳的是加密后的模型參數,因此在服務器聚合過程中,數據對服務器是“不可見”的。而且每次迭代都會更改密鑰對,即使攻擊者破解了幾輪訓練結果,也無法獲得最終結果。 綜上所述,文中所提的HEFLPS框架能夠滿足數據的隱私性和安全性要求。 本節以備受關注的新冠肺炎檢測為例,使用COVID-19 Radiography(https://www.kaggle.com/datasets/preetviradiya/covid19-radiography-dataset)數據集以及對照數據集MINIST(http://yann.lecun.com/exdb/mnist/)在分類準確率、平均加解密時長、客戶端數量對準確率的影響、通信時延、隱私保護5個方面對HEFLPS架構性能進行實驗分析,驗證該架構性能的優越性。 5.1.1 實驗環境 仿真環境硬件平臺基于3080ti GPU和64 GB內存,軟件平臺基于python3.7上運行Pythorch(v1.11.0)、操作系統為64-b Ubuntu 18.04。 每一輪實驗從模擬的客戶端設備中任意挑選5臺參與訓練,學習率為0.005,每一次本地訓練迭代次數為3次,全局迭代次數為100次,其他實驗參數的設置如表1所示。 表1 實驗參數設置 5.1.2 實驗數據集 文中采用kangle數據集網址中胸部X射線圖像數據集(COVID-19 Radiography Dataset),其中包括3 616 例新冠肺炎陽性病例以及10 192例正常肺部圖像,每張大小為299×299像素,如圖3所示。文中實驗選取3 432張圖片(80%)作為訓練集,858張圖片(20%)作為測試集,其中正常圖像(標記為0)和新冠肺炎陽性病例圖像(標記為1)以1.00∶1.15進行混合,構成文中的COVID-19數據集。 (a) 新冠肺炎陽性肺部圖像 (b) 正常肺部圖像 此外,文中采用機器學習中被廣泛用于圖像分類任務的手寫體數字圖片數據集MNIST作為對照數據集。如圖4所示,該數據集包含60 000張訓練圖片和10 000張測試圖片,每張大小為28×28像素。 (a) MNIST手寫體整體圖 (b) MNIST手寫體部分放大圖 實驗使用卷積神經網絡作為訓練模型,由2個卷積層(卷積核分別為8×8和4×4,步長為2)、2個最大池化層、1個全連接層和1個輸出層組成,使用的激活函數為ReLU。分別在兩個數據集中的測試準確率如表2所示。實驗結果顯示,文中CNN模型在兩個數據集上均能達到較高的準確率。 表2 不用數據集的模型分類準確率 文中采用聯邦平均FedAvg模型聚合方法進行模型聚合,分別在COVID-19和MNIST數據集上與傳統的集中學習進行對比,如圖5所示。集中學習的參數設置:客戶端數量和每一輪挑選的參與訓練的客戶端數k均設為1,即只有1個客戶端設備參與的聯邦訓練等價于集中式學習。其余參數配置與FedAvg一致。實驗結果表明,FedAvg的準確率能達到與集中學習近似的準確率。 圖5 FedAvg與集中式學習分類準確率的比較 在Paillier同態加密中,隨著密鑰長度的增加,安全級別會提高,但隨之而來的時間開銷也會增加。因此,文中需選擇適當的密鑰長度,來權衡安全級別和時間開銷。此外,為了提升安全級別,在每一輪訓練過程中都會重新生成密鑰對。這樣,即使某一輪密鑰被破解,也不會影響整個訓練過程的安全性,實現更高級別的數據安全。不同密鑰長度對應的時間開銷如圖6所示。 如圖6所示,實驗分別計算了密鑰長度為256、512、1 024、2 048 bit的平均加解密時長。可以看出,隨著密鑰長度的增加,時間呈現聚增現象。考慮到同態加密的安全性越高,相應的時間開銷也越高的特性,文中采用密鑰長度為512 bit對模型參數進行加密。 (a) COVID-19 (b) MNIST 文中選擇不同數量的客戶端k∈{5,10,15,20},進行分類準確率和通信時長的對比實驗,如圖7、8所示。由圖7可知,當客戶端數量較少時會產生較高的平均分類精度,同樣也能在較多的客戶端上實現較高的平均分類精度,相差約為1.9%,說明用戶數量對文中所提架構的分類精度影響不大,同時也說明用戶的離線對整體的模型精度影響不大。顯然也能從實驗結果看出,客戶端數量越少,收斂速度越快。并且由圖8可知,隨著客戶端數量的增加,聯邦通信時長也在明顯增加,當k=5時,每個用戶的時間消耗最少。因此,文中選取客戶端數量k=5作為實驗基準。 (a) COVID-19 (b) MNIST 圖8 不同客戶端數量通信時長比較 通信總時間主要來自模型加、解密的時間和等待客戶端返回結果的時間。而聯邦學習產生的等待時延主要由最慢的客戶端參與訓練的時長決定,因此。客戶端的選擇對通信時延的影響很大。文中所提方案的通信時長隨客戶端數量的變化如表3所示。 表3 優化前后通信開銷比較 s 結合表3和圖8得出,當客戶端數量增加時,時間開銷近似線性增加。在COVID-19數據集中,當C=5時,時間縮短了300 s,而當C=10時,時間縮短了445 s。同樣在MNIST數據集中,隨著客戶端數量的增加,縮短的時間也越多,即文中方案對于客戶端較多的情況體現出的優勢更加明顯。因為隨著客戶端數量的增加,客戶端出現故障的可能性也在增加,更大地縮短了服務器端的無效等待時間。 文中將Paillier同態加密和差分隱私技術分別在兩個數據集上對模型準確率進行對比實驗,如圖9所示。 (a) COVID-19 (b) MNIST 實驗結果表明,差分隱私因其對數據加入了噪聲會使數據可用性降低導致分類準確率降低;而同態加密則能保持和無隱私保護的聯邦學習一致的準確率,說明同態加密可以在提供數據高安全性的情況下,依然能保證其較高的準確率以及數據可用性。 以上實驗結果證明了文中所提的HEFLPS架構在準確率和時間開銷方面的優越性,且能夠在高準確率、低時延的情況下實現較強的隱私保護性能。 文中基于同態加密提出了一種高效的醫療數據隱私保護聯邦學習架構-HEFLPS。分別對聯邦學習參與方進行安全身份認證以及對模型參數進行隱私保護,并結合消息確認機制降低了聯邦通信開銷。在COVID-19數據集以及MNIST數據集上的實驗結果表明,文中所提架構能在保持較高分類準確率的同時實現隱私保護。但由于同態加密存在密文爆炸、密鑰過大和運行效率低等問題,在未來工作中,將進一步設計效率更高的隱私保護聯邦學習架構,更好地應用于醫療大數據的實際應用場景中。4 系統模型
4.1 總體架構




4.2 模型構建
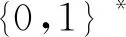
4.3 通信開銷
4.4 安全性分析
5 實驗與分析
5.1 實驗設置


5.2 模型準確率分析
5.3 平均加解密時間
5.4 客戶端數量對實驗性能的影響
5.5 通信時延
5.6 隱私保護

6 結束語

