基于流形學習的多模態水輪機溫度時間序列異常監測
楊偉業,陳 漾
(國網浙江省電力有限公司緊水灘水力發電廠,浙江 麗水)
引言
我們在這篇論文中,提出了一種時間序列異常監測的新范式——基于流形學習的多模態時間序列異常監測方法,從一種直觀的數據對齊的角度上去實現時間序列異常監測任務,使得多模態的時間序列不會被當作彼此的異常點,同時也能保證盡可能地監測到各個模態對應的異常點。并且使用了魯棒的時間序列異常監測策略[3],解決了類似于GAN 中的“模式崩潰”的問題。
1 相關工作
流形學習是表示學習中核心的一部分,流形學習有許多經典的模型,最經典的例如前饋神經網絡、卷積神經網絡,它們都有著非常強大的編碼能力以及降維能力,能夠保證將數據降維到低維空間的同時不失去一些主要的信息。transformer 是基于全局注意力機制的網絡,不僅能夠調動計算資源的并行能力,并且擁有極高的精度,因此我們使用transformer 作為我們的特征壓縮函數。
2 數據集介紹
我們的數據集稱之為“power”數據集,由水輪發電機組的94 個傳感器的溫度數據組成。一次開機所記錄的數據可以參考圖1。
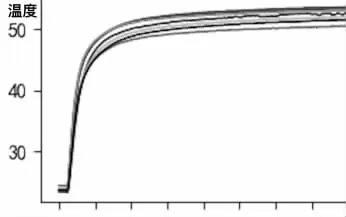
圖1 power 數據集示例
可以很明顯地看到,所有的傳感器所記錄的溫度數據都經歷了先上升后趨于平穩的過程,其中上升的過程我們稱之為“升溫階段”,平穩的過程我們稱之為“平穩階段”,并且我們將每一個過程都當作為一個“模態”,因此可以說我們的數據是“多模態”的。
3 模型局限性的證明
在這一節中,我們將通過實驗證明一系列時間序列異常監測sota 模型無法適用于多模態的時間序列數據集。 我們準備的模型分別為 Anomaly Transformer、GANF 以 及MTGFlow, 第 一 個 基 于“association discrepency”,而后兩個都是基于概率密度,數據集均為我們自己的多模態時間序列數據集“power”。
無論是Anonaly Transformer 還是GANF 或者MTG Flow,這三個模型均把一開始梯度大的部分,也就是“升溫階段”識別為異常的時間點,這是錯誤的。
我們經過分析,Anomaly Transformer 僅僅使用“association discrepency”作為評判指標,而GANF 以及MTG Flow 均僅使用“negative log likelihood”作為評判指標,而“升溫階段”以及“平穩階段”這兩個模態是屬于不同的特征空間的,因此單一的評判指標是無法泛化在不同的特征空間上的。
4 基于流形學習的模型
接下來我們將從微分動態時間彎曲、流形對齊、整體3 個部分介紹基于流形學習的模型。
4.1 微分動態時間彎曲
微分動態時間彎曲是在最原始的版本上考慮到時間序列的導數,從而建模序列之間更加自然的一一對應的關系,下面我們將簡要介紹。
給定兩個時間序列,第一個序列Q 為Q=q1,q2,...,qi,...qn,第二個序列C 為C=c1,c2,...,cj,...,cm,我們想要構建一個n*m 的臨近圖矩陣來建模兩個時間序列之間的對應關系,具體的操作步驟參考偽代碼1(見表1)。

表1 偽代碼1
其中distance_matrix()為計算q 與c 之間的歐幾里得距離,即distance(q,c)[i,j] = deriative()為近似計算時間序列導數的函數,具體表達式為,對于時間序列Q 中的某一點qi:
由于這樣得到的導數序列比原始序列的長度少一列,所以我們在導數序列的最開始復制一項
4.2 流形對齊
為了壓縮高維數據并且保留高維數據的一些主要特征,我們使用流形對齊的策略,兩個壓縮映射函數F1(Q)和F2(C),分別將Q 和C 映射到d 維空間,并且d<<dq 且d<<dc。規定以下的損失函數,使得低維特征能夠保留高維特征的主要信息:
其中,μ 為信息保留超參數;W(Q,C)為時間序列Q 和C 的微分動態時間彎曲圖鄰近矩陣;W (Q) 和W(C)分別為Q 和C 的k 鄰近圖矩陣。損失函數的第一項是為了保持不同時間序列之間的關系,第二項和第三項是為了分別保持原有時間序列的幾何結構,μ 為超參數,用來控制各項信息的保留程度。
4.3 整體
在這一部分我們將之前所述的微分動態時間彎曲以及流形對齊結合起來,構成了我們算法的主要框架,具體可以參考偽代碼2。
5 魯棒異常監測規則
5.1 梯度蒸餾
現實世界的數據集中必然包含異常的數據,為了訓練模型人工地去剔除這些異常數據是不切實際的,尤其是對于那些大型的時間序列數據集。因此,為了使得模型的訓練更加魯棒,我們采用文獻[3]中提到的“梯度蒸餾”方法,非常樸素地減少了異常數據對于模型訓練的影響,具體的做法見偽代碼2(見表2)。

表2 偽代碼2
該做法的核心思想:近似地將整個訓練集中異常數據的占比當作訓練模型時一個批次數據中異常數據的占比,并且在模型訓練梯度下降的過程中,對應的損失函數最大的數據的梯度剔除,用剩余的認為是正常的數據的梯度來更新模型的參數。這樣保證了大部分的異常數據不會參與到模型的訓練過程中,從而可以從一定程度上保證數據被降維到正確的空間。
5.2 譜歸一化
我們經過實驗發現,盡管經過了梯度蒸餾,模型還是會有“欺騙”的操作:無論是正常的數據還是異常的數據,模型都將其映射到低維空間中一個固定的點。生成器所生成的數據具有高度的相似性。而SNGAN[4]通過譜歸一化的操作很好地解決了這個問題,因此,我們在模型中也加入了譜歸一化層,使得正常數據和異常數據經過降維之后有很高的區分性。
6 實驗細節
對于流形壓縮函數F1(Q)以及F2(C),我們均采用transformer 的encoder 模塊,具體的結構如圖2 所示。
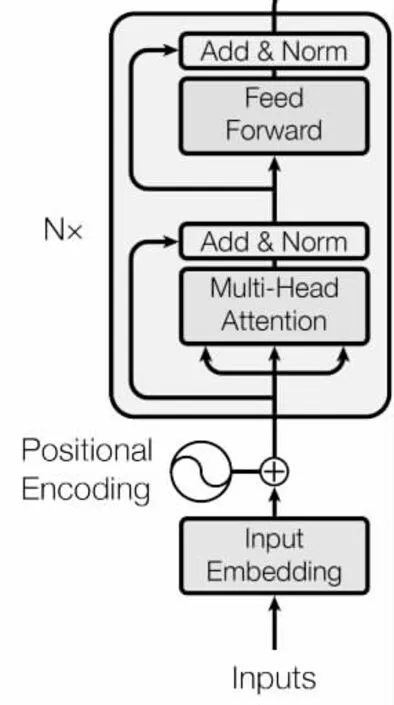
圖2 壓縮函數網絡結構
對于流形壓縮函數,我們使用超參數N 為6,使用Adam 作為優化器,學習率為0.0001,采用warm up為500 個iteration,采用學習率余弦退火,基于RTX 2070super 的GPU 環境。根據訓練集的估計,我們采用損失函數的前5%作為閾值,來進行異常點的挑選。
7 模型結果可視化
基于流形學習的模型,能夠將“平穩階段”部分的異常點監測出來,這驗證了我們的模型對于多模態時間序列異常監測任務的適用性。實驗結果查看圖3,黑色加粗位置就是識別到“平穩階段”的異常點。
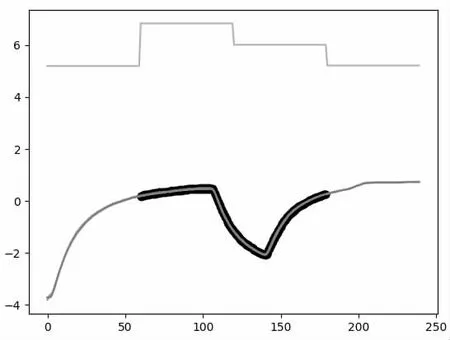
圖3 流形學習模型的異常監測
8 總結
8.1 結論
從總體上來說,我們發現了目前水輪發電機組溫度時序數據多模態異常監測的難題,提出了一個基于流形學習數據對齊的時間序列異常監測模型,驗證了升溫階段和平穩階段的異常監測,結合梯度蒸餾、譜歸一化的魯棒監測規則,使得模型的訓練不再過度依賴于純凈的數據集。
8.2 未來工作的方向
雖然我們的模型是用于多模態時間序列異常監測的模型,但是核心的思想還是非常樸素:僅僅從數據對齊的角度去解決時間序列異常監測的問題。模型在我們自己的power 數據集很有效果,但是現實中的很多時間序列數據集要比我們的power 數據集復雜的多,因此我們未來將發掘更多的多模態時間序列數據集,并且依次驗證我們的模型在這些多模態數據集上的有效性。

