基于支持向量回歸的抽油機井檢泵周期預測研究?

鄧 杰 劉新平 楊鵬磊

（中國石油大學（華東）計算機科學與技術學院 青島 266580）

1 引言

目前，在我國機械采油工藝中，有桿泵采油方式在原油開采中占據著十分重要的地位。有效降低油井檢泵率，提高油井利用率是采油工程控制成本的一個有效途徑。研究人員在抽油機井檢泵預測方面做了大量的研究工作，分析了影響油井檢泵周期的因素并提出了預防措施［1～5］。影響抽油機井檢泵因素較多。其中，文獻［6～7］從抽油桿壽命方面進行了深入的研究，文獻［8］研究了抽油機桿懸點載荷對檢泵周期的影響，文獻［9］開展了抽油機游動凡爾罩斷裂機理及防治對策研究，文獻［10］分析了抽汲參數調整對油井檢泵率的影響。由于抽油機井生產參數較多（實際檢測的生產參數20 余種），各類參數與抽油機井的檢泵因素有著直接關聯關系，但是各類生產參數之間以及各類檢泵因素之間存在耦合影響和非線性因素，難以判斷各類生產參數對抽油機檢泵周期的影響權重。同時，基于機理分析的預測模型需要與生產實際情況相結合，準確率和有效性有待進一步提高。因此，結合現場經驗，從數據挖掘的角度出發，利用油田生產數據和油井作業數據，建立抽油機井檢泵周期與各生產要參數的關系模型預測抽油機井檢泵周期，對有效降低檢泵率具有重要的研究意義。

常用的數據挖掘技術主要涉及機器學習和深度學習［11］，如線性回歸、支持向量機（SVM）［12］、卷積神經網絡［13］、循環神經網絡［14］等算法。其中，支持向量回歸（SVR）［15～16］是支持向量機在回歸領域的應用，它在解決非線性和高維問題中表現出許多特有的優勢，被廣泛應用于各種預測問題。

本文采用SVR 算法開展抽油機井檢泵周期的研究，通過對抽油機井生產數據的預處理，基于灰度關聯方法優選主要生產參數，建立抽油機井檢泵周期與主要生產參數的關系模型。

2 數據預處理

2.1 數據采集

與抽油機井檢泵因素相關的數據來源于抽油機井生產數據和檢泵作業數據。主要包括生產時間、日產液量、日產油量、含水率、上行電流、下行電流、油壓、套壓、流壓、泵徑、泵深、沖程、沖次、動液面、累產油量、累產水量、最大載荷、最小載荷、檢泵作業時間等。由于抽油機井原始生產數據存在多源、異構、缺失、重復、不準確以及各類生產參數量綱不同等情況。需要對數據預處理后開展實驗研究，有效提高模型的準確性。

2.2 數據預處理

1）數據清洗

統計分析各類生產參數的特征，掌握各類數據的范圍，有效去除各類奇異數據和錯誤數據，提高模型的有效性和準確性。抽油機井的生產參數較多，以日產液量數據統計為例，如圖1 所示，某一區域的抽油機井單井日產液量集中在15～45（t/d）范圍內。因此，當日產液量超出這個范圍后，需要分析產液量降低或是升高的因素。從而統計正常生產情況下的抽油機井的編號及數量。

圖1 日產液量數據分布圖

基于此方法，統計生產參數正常情況下的油井的型號和數量，清洗掉奇異數據，生成有效數據體，作為訓練和預測數據，提高預測模型的準確性和實用性。同時，基于程序判斷去除重復數據，若某一屬性缺失值較多，則直接刪除該屬性，若缺失值較少，則進行填充。對于數值型變量，采用中位數進行填充，對于類別型數據直接填充為“空”。

2）去量綱

抽油機井生產參數較多，數據單位不統一，如：體積單位（/m3），壓力單位（/Mpa），時間單位（/d）等。為了便于不同單位或量級的指標能夠進行比較和加權。將數據統一變換為無單位（統一單位）的數據集，采用最大-最小標準化方法消除量綱：

式（1）中：x為數據清洗后的樣本數據，xmin，xmax為樣本數據中最大值和最小值，x*表示歸一化后的樣本數據。

3 主要參數提取

各類生產參數對抽油機井檢泵周期影響權重不同。如果將全部生產參數作為自變量會增加計算負擔，提高模型的復雜程度，降低準確率。因此，采用灰度關聯方法優選與檢泵周期關聯性較大的參數做為自變量。通過灰度關聯分析算法，可得到特征值（子序列）與周期（母序列）關聯度大小的排序，關聯度越高則表示兩個因素變化的趨勢具有強一致性，即同步變化程度越高。子序列的各個指標與母序列的關聯系數計算方法如下：

式（2）中，ρ為分辨系數，0<ρ<1，若ρ越小，關聯系數間差異越大，區分能力越強，通常ρ取0.5；x0(k)和xi(k)分別表示母序列第k 個數和子序列第i個特征值的第k個數；ζi(k)則表示第i個特征的第k個值與母序列第k個值的關聯系數。通過關聯系數來計算關聯度再進行最后的排序。其中關聯度得計算如下：

式（3）中，ri為第i個特征與母序列的關聯度大小，n 為樣本數量。基于計算結果，對所有ri進行排序即可得到關聯度排序。通過使用灰度關聯分析算法選擇的主要參數為日產液量、沖程、沖次、泵徑、泵深、沉沒度、含水率、最大載荷、最小載荷。其所選參數與因變量之間關聯度如表1所示。

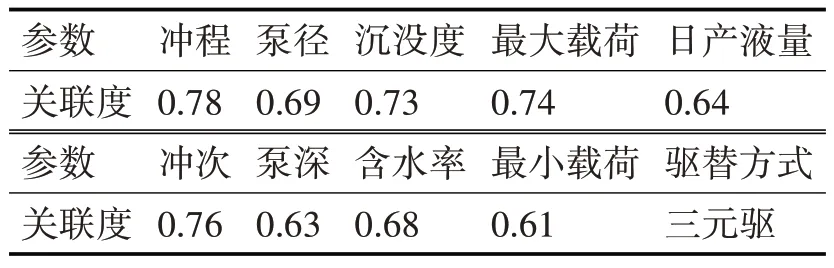
表1 特征參數關聯度表

4 預測模型

基于SVR的油井檢泵周期預測模型的函數為

式中，w為權值向量，?(x)為非線性映射函數，b 為偏置向量。由于SVR存在容忍偏差ε，于是SVR問題可形式化為

其中，C為正則化常數，Loss為損失函數：

為了確保大部分數據參與模型訓練，引入松弛變量ζi和，則式（5）優化為

由拉格朗日乘子法可得拉格朗日函數：

在KKT條件下，拉格朗日的對偶形式為

將其對偶形式求解獲得回歸函數為

其中，K(xi,xj)=φ(xi)Tφ(xj)為核函數。在SVR 周期預測模型中，核函數K（x，x）的類型對模型的性能影響較大，可以通過比較不同核函數的性能情況來選擇最佳的和函數類型。

5 實驗結果

將原始數據經過清洗、歸一化以及參數優選后開展周期預測建模實驗。對數據樣本進行隨機劃分，訓練集占70%，測試集占30%。如果經過生產參數優選，控制算法參與遍歷優化后仍不能達到預期準確率（預期準確率為85%以上），重新開展數據預處理和主要參數提取步驟，過程如圖2所示。

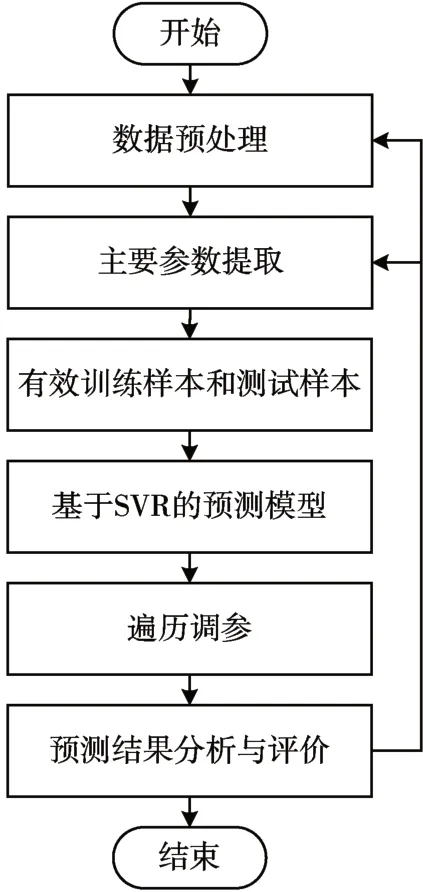
圖2 模型構建流程圖

實驗分別測試了在不同核函數下以及不同的算法下的模型準確率。常見的核函數類型有線性核函數、多項式核函數、徑向基RBF 核函數和Sigmoid核函數。當選取不同的核函數時，模型準確率如表2所示。

表2 核函數的選取

選擇SVR 模型的核函數為Rbf，遍歷SVR 模型參數C 的范圍為（0.01，100）此時參數gamma 設置為默認值，即：1/n_features，其中n_features 為輸入特征數量，從圖3 可知當C 為9 時準確率最高，為86.55%。

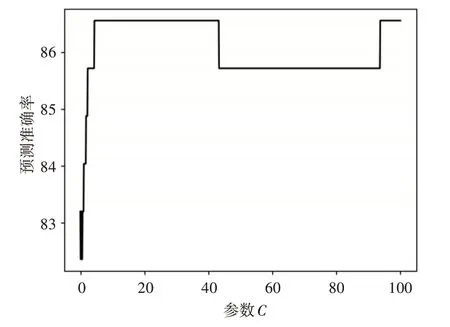
圖3 遍歷參數C實驗圖

確定C 值后，再遍歷參數gamma 的范圍為（0.01，10），從圖4可知gamma為1.8時結果最優。

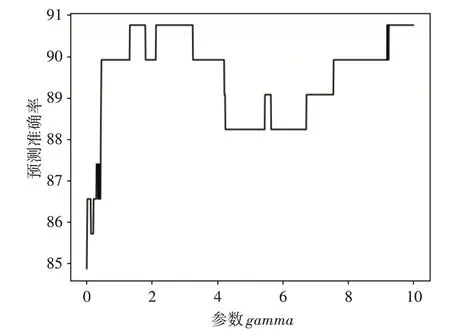
圖4 遍歷參數gamma實驗圖

確定各項參數后，仿真結果如圖5 所示，模型預測結果準確率高達90.76%。

圖5 SVR預測示意圖

基于實驗數據，測試了多元線性回歸算法，BP神經網絡算法，并將模型預測結果與SVR算法相比較。實驗結果如表3所示。

表3 三種算法預測誤差對比情況

模型的平均絕對誤差值：

模型的平均相對誤差值：

其中m 為數據量，h(xi)和yi分別為預測值和真實值。基于SVR 的檢泵周期預測結果準確率率為達到了預期目標，與多元線性回歸算法和BP 神經網絡算法相比較，獲得了較好的預測結果。

6 結語

本文從數據挖掘的角度出發，采用灰度關聯算法，優選了抽油機井主要生產參數，基于SVR 算法開展了抽油機井檢泵周期預測的實驗研究，建立了檢泵周期與生產參數之間的關系模型，獲得了較好的實驗結果。將大數據分析方法與油田措施業務相結合，充分挖掘數據價值的可行性和有效性，為智慧油田建設提供了新的研究方向，拓展了解決工程技術難題的思路和方法。同時，在實驗過程中，由于數據噪聲的影響，人工檢泵質量不同，多因素檢泵等因素共存，對檢泵周期的預測和分析影響極大。