基于聚類分析和支持向量機的非等間隔應力譜編制方法

薛 海，杜 文，尹懷彥，胡李軍

(蘭州交通大學機電工程學院，甘肅，蘭州 730070)

實測的應力-時間歷程綜合反映了結構在實際服役條件下所受的載荷和環境信息，但由于其隨機交變性，不宜直接用于結構的疲勞壽命評估或疲勞試驗[1-2]，需采用計數方法對應力-時間歷程進行應力循環統計處理，編制能真實反映應力信息的應力譜，獲得各級應力大小與其出現次數的關系[3-4]。

分級是應力譜編制中需要解決的關鍵問題之一，若級數過少，過大的應力區間改變了應力循環特征，導致分組后每個新的應力循環產生的結構疲勞損傷與實際結果產生的疲勞損傷存在差異；級數過多，一方面不宜應力譜的工程化應用，另一方面在中高應力區出現次數為零的應力級使得總體統計特性較差。傳統方法是基于樣本直方圖進行分級，如Moore 公式、Sturges 公式、Doane公式等，僅僅是從數學角度進行考慮，忽略了應力作用于結構所造成的疲勞損傷，缺失工程邊界條件的考慮。目前在工程應用中，國內外的分級方法主要基于等間隔和非等間隔兩種方法開展研究和應用。在等間隔分級方面，高延杰等[5]根據載荷-時間歷程采用雨流計數法得到所有的載荷循環，并對每個循環的均值和幅值進行統計分析，編制了等間隔16 級載荷譜；ZHANG 等[6]通過統計應力幅值和均值的分布特性，建立了幅值等間隔的8 級譜；孫晶晶等[7]基于提速客車轉向架構架實測載荷-時間歷程，應用雨流計數法編制構架等間隔8 級載荷譜。非等間隔分級中，劉永臣等[8]通過雨流計數獲得輪式裝載機載荷的均值頻次和幅值頻次分別服從正態分布和威布爾分布的擬合數學模型，編制了非等間隔8 級載荷譜；PRATUMNOPHARAT等[9]采用短時傅里葉變換和小波變換的方法，根據分解信號的累積功率譜密度提取造成結構疲勞損傷貢獻大的部分，在此基礎上編制了非等間隔8 級載荷譜；高云飛等[10]基于雨流計數法，通過假設檢驗確定應力分布數學模型，編制了非等間隔8 級齒輪程序應力譜。但上述等間隔方法未考慮編譜前后造成的損傷誤差，且級數的確定科學依據性欠佳，而非等間隔分級均采用固定比例系數編譜，得到的疲勞損傷與實際差異較大，且在編譜中分級數沒有明確的統一標準。同時，載荷譜編制中也有機器學習算法應用，但機器學習算法主要用在載荷樣本數據較小、不能全面反映結構受載特性的情況下進行載荷譜的外推或預測，如楊博文等[11]和霍軍周等[12]通過采用BP 神經網絡算法，建立載荷譜預測模型，有效模擬了實測或仿真過程中未表征的載荷信號，提高了載荷譜的精度。

針對上述存在的問題，本文根據實測的應力-時間歷程建立疲勞損傷與應力譜分級數的數學模型，以損傷相對誤差和分級準確率為分級依據，采用聚類分析和支持向量機進行應力譜編制，并與目前常用的等間隔和非等間隔應力譜編制方法所造成的疲勞損傷進行比較，驗證該方法編制應力譜的可行性。

1 基于疲勞損傷的分級模型

應力譜主要用于承載結構的疲勞損傷分析，為此，在應力譜的編制過程中，分級數的確定要盡可能體現應力循環所造成的疲勞效應，使編制的應力譜在便于應用的情況下盡可能降低與實際疲勞損傷的誤差。

由于以雙參數為基礎的雨流計數法是基于材料的應力-應變遲滯回線進行應力統計，較好反映了材料的疲勞損傷特性[13]。為此，采用雨流計數法得到每個應力循環的均值和幅值，根據材料的S-N曲線和線性累積損傷理論，推導得到每個應力循環所造成的損傷Di為：

式中： σi為每個循環的等效應力；ni為 σi對應的循環次數；m、c為材料相關參數。

為了根據有限的級數盡可能準確地反映應力分布特性，且減小所編制應力譜造成的疲勞損傷與實際損傷差異，建立疲勞損傷和應力譜分級數的數學模型。對比不同分級數編制的應力譜所造成的損傷與實際損傷，選取最接近實際損傷的分級數可有效降低因應力譜分級數選取不合理導致的誤差。目前非等間隔應力譜分級方法采用8 級進行描述，其各級應力按最大應力σmax的1 倍、0.95 倍、0.85 倍、0.725 倍、0.575 倍、0.425 倍、0.275 倍、0.125 倍進行階梯劃分[14-15]，但在實際分級中，8 級不一定為最佳分級數，故為了更準確對實測應力數據進行非等間隔分級，引入各級應力自適應比值系數 βj進行各級等效應力 σej的確定。

若對雨流計數得到的每個應力循環不進行分級處理，則保留了每個應力循環的特征，能真實反映實際應力所造成的損傷。為此，根據每個應力循環所造成的損傷Di表達式(1)和各級應力與最大應力的關系表達式(2)，推導得到不進行分級的應力循環所造成的總損傷D1和非等間隔分級造成的總損傷D2分別為：

式中：n0為應力循環總次數；s為非等間隔分級數；nj為第j級對應的循環次數。

當實際總損傷D1和非等間隔分級造成的損傷D2相等或相對誤差較小時，說明所確定的分級數是合理的。由于應力的分級歸類改變了應力循環特征，所編制的應力譜與實際應力循環所造成的損傷存在誤差，故采用相對誤差τ進行最佳分級數的確定。

2 應力循環聚類分析

經雨流計數后，每個應力循環不同于原始應力-時間歷程，由連續信號變為離散應力循環。采用目前等間隔分級方法歸類時，由于提取的應力循環分散性，容易出現次數為零的應力級，且應力譜編制方法缺少根據應力本身的屬性特征進行分級，導致產生的損傷與實際結果差異較大，與實際不符。聚類分析方法是根據樣本本身的屬性特征進行歸類，很大程度保留了樣本原來的特性[16]。故采用聚類分析法，以每個應力循環的等效應力為指標特征，對所有的應力循環進行聚類。

通過計算每兩個應力循環間的距離度量其相似程度，各應力循環間的距離為：

對于各類之間的合并，采用離差平方和法，該方法適用于多因素、多指標的分類和特征識別，能依據每個循環等效應力的特征進行分類，以體現每個應力循環之間的綜合差異。

若應力譜分級數為s，將n0個應力循環分成s類，分別記為G1,G2,···,Gs，采用Cti表示第t類Gt中的第i個應力循環的等效應力，nt表示該類包含的應力循環數，表示Gt的均值，則Gt類的離差平方和St為[17]：

對于任意兩類Gα、Gβ，對應的離差平方和分別為Sα和Sβ，合并為一類，記為Gr，則Gα與Gβ之間的平方距離為：

合并后的Gr對應的離差平方和Sr滿足式(10)～式(12)。

通過對合并后的Gr依據式(10)～式(12)進行推導，得出：

從而由式(8)得兩類間的平方距離為：

對所有類依次進行合并，并循環計算，直至所有應力循環合并為一類，從而得到任意一類Gξ與合并后的Gr的離差平方和距離遞推表達式為[18]：

通過上述步驟將所有應力循環的等效應力進行聚類，從而實現所有應力循環不同類別的歸類。在實際應力譜編制中，分級數基本選取4 級、8 級、16 級、32 級、64 級等[19]。因此，將所有循環聚成4～64 類，得到不同分類數下各類的應力循環數。

3 分類效果評估

由于聚類分析是無監督分類方法，缺少明確的理論依據判斷分類結果的準確性，而支持向量機在多分類判別中具有優良的性能，相對于神經網絡、最鄰近等分類算法，能比較準確反映不同類別的分類效果[20]。因此，采用支持向量機的多分類預測得到的分類準確率評價聚類分析中不同類別下的聚類效果。

假設選定部分應力循環 {σ1,σ2,···,σn'}為訓練集，其中類別數為yi={1,2,···,s}，共s類，通過訓練后決策函數f(x)對剩下的應力循環進行分類，得到訓練集和預測集的分類準確率。

每兩個不同類別應力循環構成一個分類器，對于任意第i類和第j類應力循環，其最優分類面為[21]：

為了在任意兩類之間構造一個分類器，求解其二次規劃問題，約束條件為：

式中：ω為行向量； φ表示輸入空間到特征空間的非線性映射； ξ為松弛變量；P是懲罰系數。

由于變換 φ的核函數為K(σi,σj)，則式(15)～式(16)的對偶問題轉化為求解目標函數的最小值[22]：

添加其約束條件為：

采用Lagrange 乘子最優化方法將函數f(α)在支持向量上展開，求得最優解選取 α*中的一個分量，可得分類閾值b為：

構造第i類和第j類應力循環的支持向量機決策函數為：

采用高斯徑向基核函數K(σi,σj)進行支持向量機分類，其表達式為：

式中： δ為尺度參數； α為Lagrange 乘子。

根據決策函數判別訓練集應力循環是屬于i類還是j類，并將屬于類別i的數據標記為正，屬于類別j的數據標記為負。通過該算法不斷循環對所有測試集應力循環的等效應力經支持向量機投票決策，采用式(23)計算不同分類結果下的分類準確率η：

式中：n1為訓練集樣本訓練結果與實際類別一致的樣本數量；n2為測試集樣本預測結果與實際類別一致的樣本數量；n0為總的樣本數量。

分類準確率越接近100%，說明聚類效果越好，故通過分類準確率大小進行聚類效果的評價。

4 實例應用

4.1 應力譜編制

根據上述方法，對某型地鐵焊接構架電機吊座根部實測應力-時間歷程數據進行應力譜編制，取焊接構架疲勞性能參數m值為3.5[23]。為避免頻混導致采樣信號的失真，根據信號采集相關理論和構架隨車振動頻率，設置采樣頻率為2000 Hz。

由于小應力在疲勞損傷計算時基本不產生損傷，故對實測信號中的小應力進行處理，通過MATLAB 小波工具箱，選用haar 小波，進行信號5 層小波分解，取應力幅值變程的5%作為小波處理閾值[24]，剔除不產生損傷的大量小幅值信號，在保留了應力整體趨勢的基礎上，提高了應力循環統計效率。小波處理前后對比如圖1 所示。

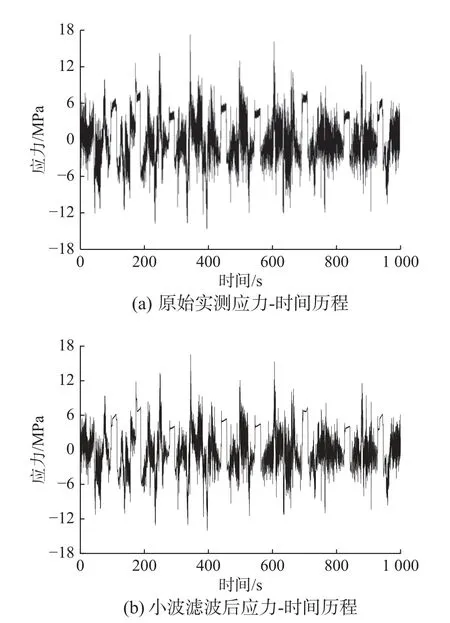
圖1 應力-時間歷程處理前后對比Fig.1 Comparison of stress-time history before and after processing

通過聚類分析，將所有的載荷循環樣本分成4～64 類，以聚為16 類為例，取各類樣本的應力平均值為等效應力，則對應的各類樣本循環數如表1 所示。

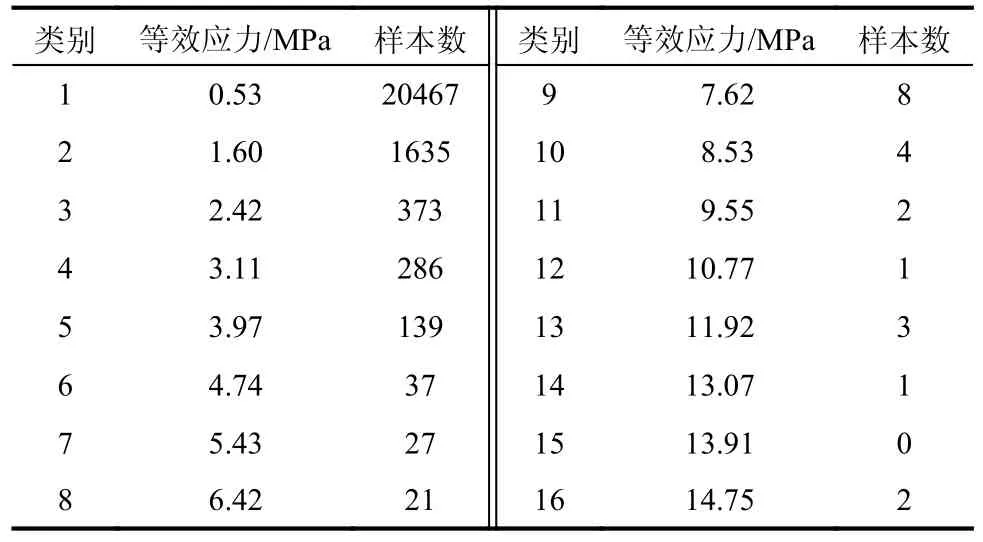
表1 聚類分析分為16 類時各類樣本數Table 1 The number of samples of each type when cluster analysis is divided into 16 categories

雨流計數得到的應力循環經聚類分析，通過建立的疲勞損傷數學模型表達式(5)進行計算，得到不同分級數對應的損傷相對誤差，并將聚類分析所得分類的應力循環50%作為訓練集，剩下50%的作為測試集，進行支持向量機多分類判別，獲得應力譜在不同分級數下的分級準確率與損傷相對誤差，結果如圖2 所示。

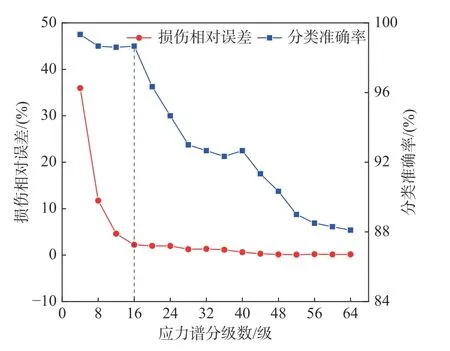
圖2 分級數-準確率/相對誤差關系Fig.2 Classification numbers-accuracy/relative error relationship

從圖2 可得出：

1)隨著分級數的增加，應力造成的損傷相對誤差逐漸減小，相對每個應力循環所造成的損傷總和，分為16 級時損傷相對誤差為2.22%，大于16 級時損傷相對誤差基本小于2.00%。

2)隨著分類數增加，聚為16 類時分類準確率為98.67%，大于16 類時分類準確率基本低于97.00%，其主要原因是隨著分級數的增多，更能保留應力循環的特性，使得所得的疲勞損傷更接近實際值，而級數過多使得支持向量機分類判別的波動性和分散性增大，導致分類準確率降低。

綜合考慮分類準確率和損傷相對誤差，為便于疲勞損傷計算，取編制應力譜的分級數為16 級，用支持向量機訓練得到的模型預測測試集的分類類別，獲得了16 級下的分類預測圖，如圖3 所示。

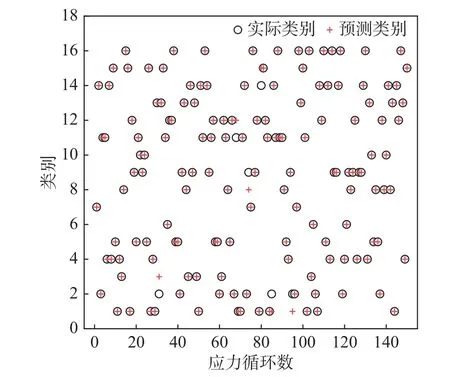
圖3 支持向量機分類預測圖Fig.3 Support vector machine classification prediction map

從圖3 可以得出：分級數為16 級時，應力的測試集分類預測與聚類分析的得到的分類結果吻合度達到98.00%以上，表明在該分類數下聚類效果較好。

通過式(2)計算應力譜非等間隔分級數為16 級時各級應力對應的自適應比值系數 β，得到圖4 所示的應力-比值系數-循環次數關系，自適應比值系數從小到大依次為0.007、0.050 、0.116、0.173、0.226、 0.292、 0.359 、 0.429、 0.512、 0.562、0.613、0.687、0.758、0.863、0.931、1.000。采用上述方法所得的結果與目前等間隔編譜所得的損傷進行對比，結果如表2 所示。

表2 不同分級方式下16 級應力譜損傷比較Table 2 Comparison of 16-level stress spectrum damage under different grading methods

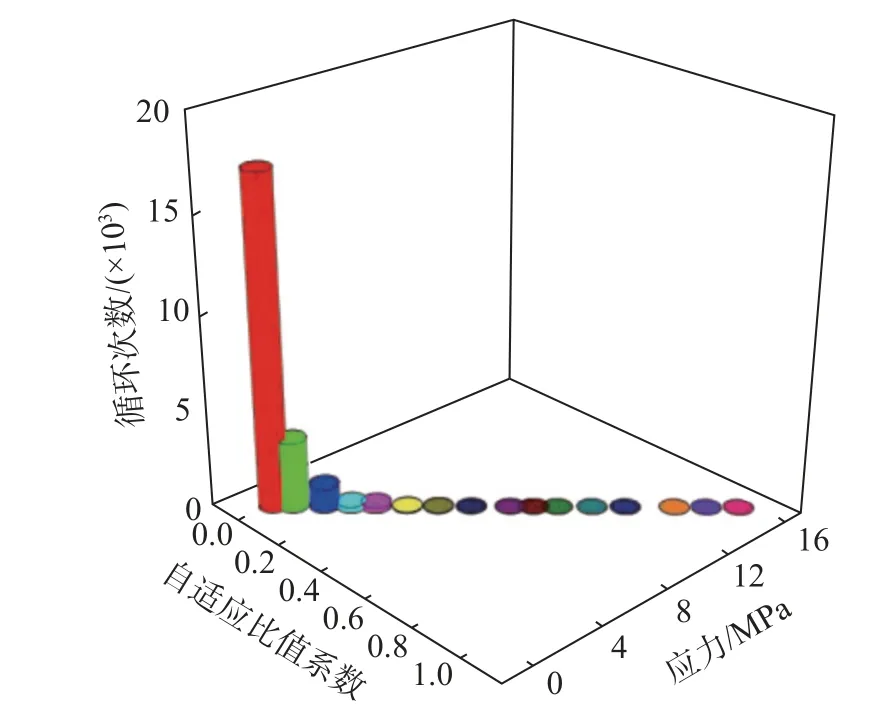
圖4 應力-比值系數-循環次數Fig.4 Stress-ratio coefficient-cycle number

從圖4 和表2 可得出：

1)通過聚類分析和支持向量機得到的各級應力及比值系數是基于疲勞損傷模型，與目前應力譜編制方法差別較大。

2)該方法進行編譜是根據應力本身特性和造成的疲勞損傷進行分級編制，與目前等間隔分為16 級進行編譜比較，損傷相對誤差降低了7.43%，有效降低了實測應力信號由于隨機性和分散性造成的編譜偏差。

4.2 應力譜有效性驗證

由于目前編譜采用的非等間隔固定比值系數法只有8 級譜，且等間隔常用8 級譜進行結構應力譜的編制，故為了驗證本文所采用方法編制的應力譜有效性，取分級數為8 級所編制的應力譜與目前等間隔和非等間隔編譜方法進行對比驗證。

采用目前非等間隔固定比值系數法進行應力譜編制時，參考文獻[25 - 26]對各級頻次計算方法，取最大應力對應次數為1，其他各級頻次ΔN=Nj-Nj-1(j=2, 3, …, 8)，由于通過該方法編制應力譜時，最小應力級為最大應力的0.125 倍，使得低于最小應力的大部分小幅值應力被舍棄，獲得的應力譜在進行疲勞問題分析時提高了計算效率和實用性。為了便于對比分析，采用其他分級編譜方法前對小載荷的處理方法與目前非等間隔小載荷的舍棄保持一致，得到不同分級方法下分級數為8 級的結果，如表3 所示。

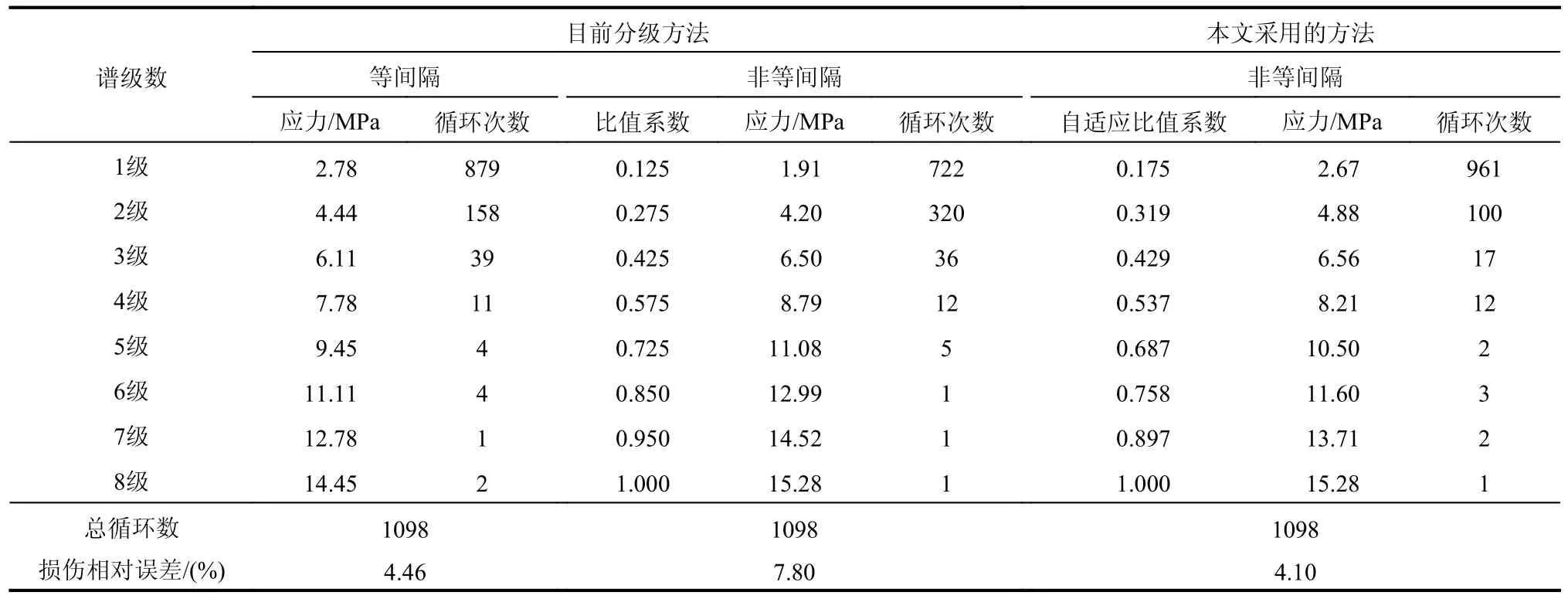
表3 目前分級方法與本文編譜方法分析比較Table 3 Comparison of the current grading method and the proposed compiling method

從表3 得出：采用常用的8 級譜進行編譜時，本文采用的編譜方法得到的疲勞損傷相對誤差為4.10%，相對于目前等間隔和非等間隔編譜，損傷誤差分別降低了0.36%和3.70%；相對于目前等間隔分級方法，該方法保留了實測數據的最大應力，得到最大應力級為15.28 MPa，目前等間隔最大應力級為14.45 MPa。

通過比較驗證，表明本文所采用的編譜方法不僅很大程度上保留了應力的分布規律，且能比較準確的反映應力疲勞特性。

5 結論

本文通過采用聚類分析和支持向量機方法，引入自適應比值系數，提出了一種基于疲勞損傷的非等間隔應力譜編制方法。以某型地鐵焊接構架電機吊座根部實測應力-時間歷程數據為例，根據本文應力譜編譜方法和傳統分級方法進行比較，驗證了本文編譜方法的可行性，并得出以下結論：

(1)考慮不同分級數和分級方式對疲勞損傷的影響，根據損傷一致原則，引入各級應力自適應比值系數，建立應力譜非等間隔分級數學模型，確保了應力級數確定的科學性；

(2)通過聚類分析對所有應力循環進行判別歸類，可得出各循環等效應力間的分布規律是影響聚類效果最主要的因素，且隨著分類數的增多，特征相近的應力可歸為一類；

(3)隨著分類數的增加，支持向量機構造的分類器增多，類別預測效率降低，自成一類的大幅值應力循環增多，導致其分類準確率減小；

(4)通過引入自適應比值系數，采用聚類分析和支持向量機，提出的基于疲勞損傷的非等間隔分級方法，提高了所編制應力譜的準確性，可為載荷、加速度、位移等其它信號的編譜過程提供參考，以此提高結構疲勞設計和評估的準確度。