五階遞進的最短路徑問題教學模式探索

許項東 徐詠蕾 鄒曉磊 滕靖

摘? 要：最短路徑問題是計算機科學、地理信息科學、運籌學、管理科學、交通工程、工業工程和復雜系統科學等領域的基礎性問題，也是許多相關課程中的教學重點。針對目前教學中存在的被動接受、手工計算、只算不用等問題，按照“精選算法、縱向到底、橫向到邊”的教學理念，探索“算法原理—數學建模—應用舉例—程序實現—算法比賽”五階遞進的最短路徑問題教學模式，有助于培養和提升學生的原理掌握深度、優雅學術品位、運籌優化思維、綜合應用能力和團隊合作精神。

關鍵詞：圖論；最短路徑；數學建模；Dijkstra算法；應用舉例

中圖分類號：G642? ? ? 文獻標志碼：A? ? ? ? ? 文章編號：2096-000X（2023）32-0032-04

Abstract： The shortest path problem is a fundamental problem and a core knowledge module in many disciplines， such as computer science， geographic information system， operations research， management science， transportation engineering， industrial engineering， and complex system science. It is also the focus of teaching in many related courses. According to the teaching concept of "selecting algorithms， vertical to the end， horizontal to the edge"， this paper explores the five-step teaching mode of "algorithm principle - mathematical modeling - application example - program realization - algorithm competition" for the shortest path. It is helpful to cultivate and enhance students' in-depth grasp of principles， elegant academic taste， operation and optimization thinking， comprehensive application ability， and team spirit.

Keywords： graph theory; shortest path problem; mathematical modeling; Dijkstra algorithm; applications demonstration

基金項目：上海高校市級重點課程建設項目“《運籌學》”（無編號）；上海高校課程思政領航課程建設項目“《運籌學》”（無編號）

第一作者簡介：許項東（1985-），男，漢族，安徽霍山人，博士，教授，博士研究生導師。研究方向為交通運輸網絡建模與優化、交通系統韌性。

最短路徑問題的目標是，在網絡中給定兩節點之間找出一條總權重之和最小的路徑[1]。作為圖論中最為經典與最常見的問題之一，最短路徑問題是計算機科學、地理信息科學、運籌學、管理科學、交通運輸工程、工業工程和復雜系統科學等領域的研究理論基礎，其核心思想與日常生活中的交通導航、救災搶險、工程管理等密切相關，成為許多相關課程的教學重點。

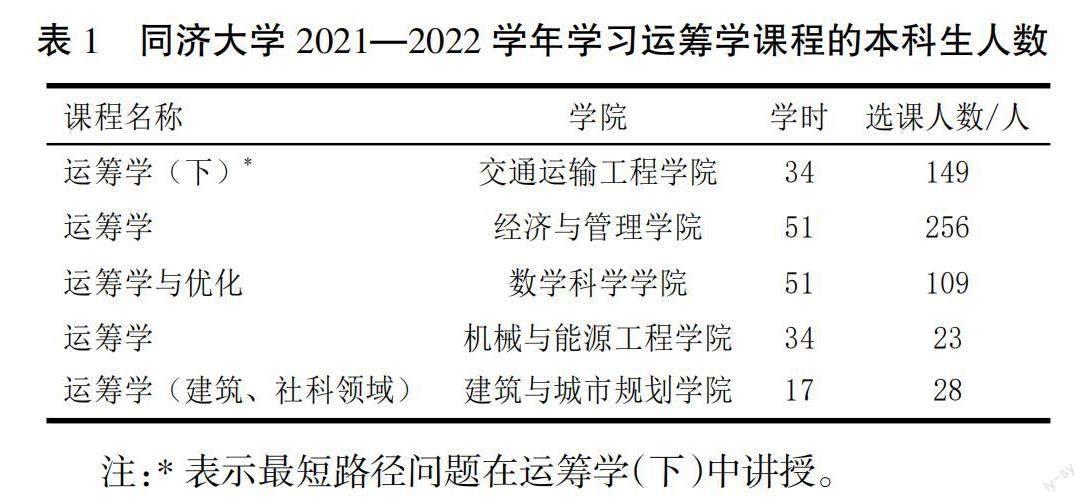
最短路徑問題是運籌學課程的基本內容和教學重點。以同濟大學為例，如表1所示，開設運籌學課程的學院和專業主要有：交通運輸工程學院的交通工程、交通運輸專業，經濟與管理學院的物流管理、信息管理與信息系統、市場營銷等專業，數學科學學院的統計學、數學與應用數學專業，機械與能源工程學院的工業工程專業等。需要指出的是，這里僅統計了運籌學類課程。其他課程中也可能涵蓋最短路徑問題，如計算機相關專業的數據結構與算法課程。

由于最短路徑問題模型目標明確、求解算法啟發性強、與其他問題結合度高及應用場景廣泛，是一個培養創新思維和實踐能力的絕佳教學點。然而，在目前的最短路徑問題教學中，“被動接受、手工計算、只算不用”的問題仍普遍存在，學生們的綜合能力與應用水平有待提高。在內容上，重課本輕實踐，實際問題的數學抽象能力較弱[2-3]；在思維上，重解題輕原理，只會快速解題而舉一反三能力欠缺；在方法上，重手算輕程序，不會主動應用計算機與先進工具來輔助求解[4-5]。上述問題使得我們的教學實際效果難以滿足新時代對高校人才培養的要求，尤其是與研究型大學培養創新精神與實踐能力兼備的人才目標存在較大差距[6]。本教學團隊經過多年的教學探索和迭代反饋，初步形成并較為成功地實踐了可復制可推廣的“算法原理—數學建模—應用舉例—程序實現—算法比賽”五階遞進的最短路徑問題教學模式，以期給其他有類似問題的本科課程教學以方法上的參考。

一? 五階遞進的最短路徑問題教學模式

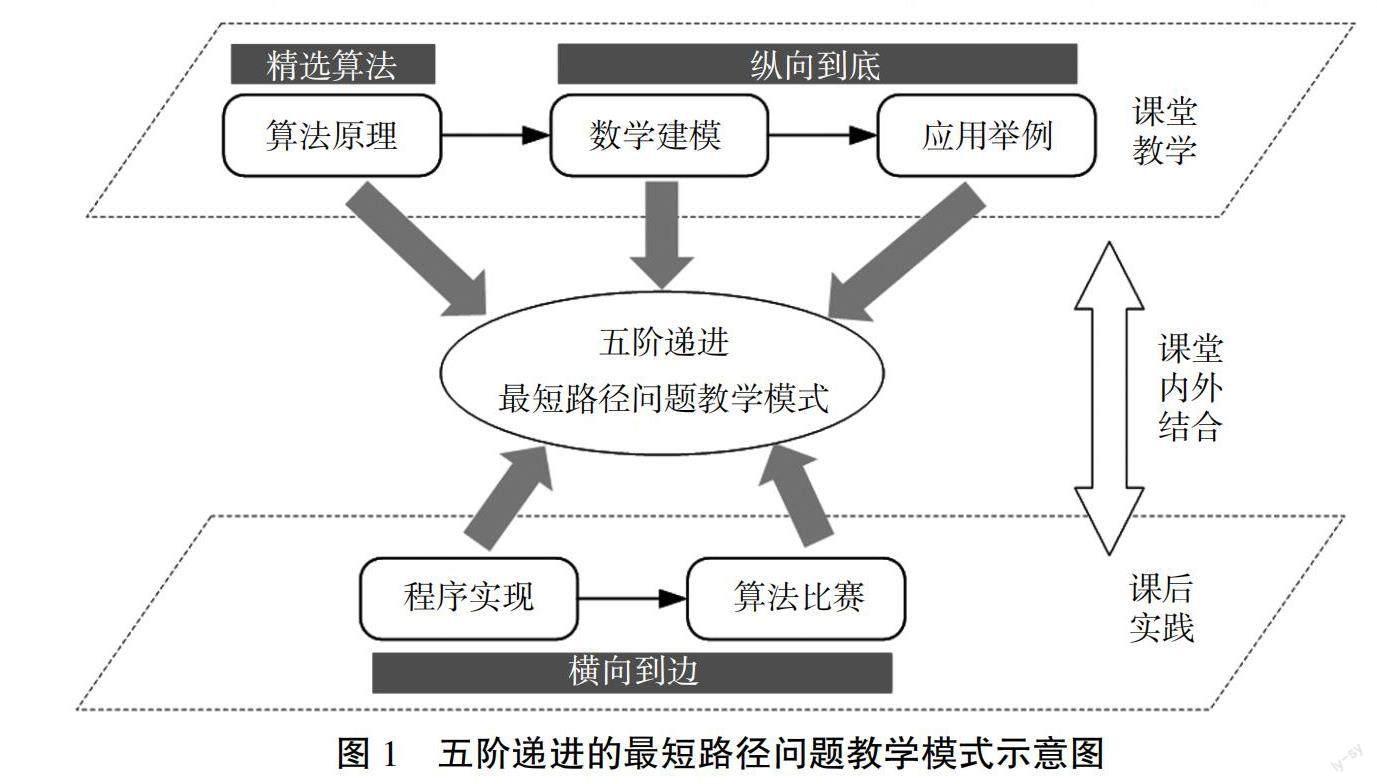
針對現有最短路徑教學中存在的問題，我們基于“精選算法、縱向到底、橫向到邊”的教學理念，提出了“算法原理—數學建模—應用舉例—程序實現—算法比賽”五階遞進的最短路徑問題教學模式，如圖1所示。其中，“算法原理、數學建模、應用舉例”主要為課內教學部分，從概念到方法再到實例，由淺入深、層層遞進。考慮到最短路徑算法譜系較為復雜，通過“精選算法”，為學生講細講透一種經典算法原理，夯實基礎理論。按照“縱向到底”的理念，深入介紹其數學規劃模型與實際應用，幫助學生深化理解算法。“程序實現、算法比賽”則為課外實踐部分，基于“橫向到邊”的思想，從小規模測試網絡的算例實驗，到大規模真實網絡（所在城市的道路交通網絡）的算法設計與優化，引導學生化被動為主動，注重提升學生的實踐應用能力與創新思維，以及加強與前修課程的綜合理解。通過課堂內外相互促進、相互結合的形式，形成五階遞進的最短路徑問題教學模式。

在最短路徑問題引入方面，考慮到筆者的課程教學對象是交通運輸工程學院的本科生（包括交通工程專業、交通運輸專業），我們引入了日常生活中常用且也是交通運輸工程的前沿應用場景——車輛路徑導航（包括未來自動駕駛的路徑導航）。

最短路徑問題的具體算法有著較為豐富和成熟的譜系，可按照以下三類進行細分[7]：①問題類型（Problem Type），如針對單源最短路徑的Dijkstra算法，針對多源最短路徑的Floyd算法；②輸入網絡特征（Input Network Characteristics），如針對無向網絡的Minty算法、針對整數弧長的Dial算法；③求解策略（Solution Techniques），如針對網絡變化時最短路徑更新迭代的Loubal算法、應用模擬計算機技術的Klee算法等。

在教學實踐中，我們遵循“精選算法、縱向到底、橫向到邊”的教學理念。其中，“精選算法”指的是，我們在課堂教學中重點介紹最為經典且常用的Dijkstra算法，對其他算法只簡單提及，留給學生課后自學和拓展；“縱向到底”指的是我們不僅講授Dijkstra算法的執行步驟，更啟發學生理解算法基本原理和數學規劃建模過程，引導學生品味該算法的創新之處和優雅之美；“橫向到邊”指的是，我們引導學生利用熟悉的計算機語言來編寫Dijkstra算法的代碼，結合大規模真實交通網絡，挖掘算法結果所蘊含的管理洞見，并通過以小組為單位的算法比賽培養和提升學生的綜合應用能力、團隊合作精神。

經過多年的教學實踐，在算法原理環節提升了學生的優雅學術品位；通過介紹最短路徑問題的數學規劃建模，引領學生形成看透問題本質的意識；通過貼近專業方向的多個應用舉例，幫助學生開拓聯想創新思維；通過程序實現，鍛煉學生的綜合應用能力，再通過算法實現，積累了學生團隊合作與創新實戰經驗。

二? 教學設計與實踐

（一）? 算法原理——優雅學術品位

在算法原理部分，我們依循經典運籌學教材的講解思路，介紹最短路徑問題的數學定義、經典Dijkstra算法（包括適合初學的圖上作業法、適合程序實現的表上作業法）等。在介紹算法原理的同時，我們注重引入算法的發展演化歷史，引導學生思考不同算法的優缺點和適用條件，培養學生的優雅學術品位。如用枚舉法亦可找到最短路徑，但并不高效，計算機技術的進步催生了更簡便高效的算法，使得最短路徑問題的求解更加簡潔巧妙。

（二）? 數學建模——探求問題本質

在現有的經典運籌學教材中，最短路徑問題部分少有介紹其數學規劃模型，我們在教學中適度介紹最短路徑問題的數學規劃模型。之所以在教學中涉及最短路徑問題的數學建模，是為了幫助學生進一步了解最短路徑問題的本質，深化對最短路徑算法的理解。在研究現實世界的很多復雜問題時，通常是先進行數學建模，然后針對模型開發高效的求解算法。

作為數學規劃模型，涉及變量、目標函數、約束條件等三要素。在教學中，引導學生思考最短路徑問題的變量、目標函數、約束條件分別是什么。決策變量的選取，直接決定模型是否需要計算量和存儲量高昂的路徑枚舉。按照最短路徑問題的定義，一般將表征每個邊是否被選入最短路徑的0-1整數變量作為求解變量，目標函數是全網所有被選中邊的總成本最小，約束條件需要確保所有被選中邊可以構成從起點到終點之間唯一的一條路徑，即從起點有且只有一條邊被選中，中間節點（非起點、非終點）的流入和流出守恒，進入終點有且只有一條邊被選中。尤其要關注，該模型的0-1整數求解變量可等價松弛為非負連續變量，從而將0-1整數線性規劃問題轉化為更易求解的線性規劃。引導學生體會，在對模型進行求解前，非常有必要“三思而后行”，避免“Garbage in， garbage out”現象，盡可能降低模型的復雜性，在算法的通用性和定制化之間作出合適的取舍。

（三）? 應用舉例——聯想創新思維

根據筆者的科研經歷，學習經典問題的目的可能包含：①學習經典問題的創新思想，豐富自己解決問題的工具箱（toolbox）；②現實中遇到的問題往往比經典問題更加復雜（例如，電動車的路徑規劃、自動駕駛車的路徑規劃），需要針對這些問題的特征，對經典問題的模型和算法進行二次創造；③將看似沒有關系的其他問題“轉化”為經典問題，這需要對經典問題有著深刻的理解。

針對我們的教學對象——交通類本科生，我們設計了多個應用舉例。

1）路面更新問題：道路路面每年的養護費用和階段性大修費用隨路面使用年限的增加而變化，需要決策在路面設計年限里的更新計劃，使得總費用最小。

2）火車售票處選址問題：現準備在七個居民點中設置一個售票處，已知各點之間的距離。問售票處設在哪個居民點，可使最大服務距離最小？若設置兩個售票處，應設在哪兩個居民點？

3）“全有全無”交通分配問題：已知某城市各交通小區之間的出行需求和路網（包括各條道路上的行程時間）。需要把這些出行需求按照行程時間最少的路徑（即全有全無）分配到路網各條道路上。

4）幾類限制條件下的最短路徑問題：如，找一條不通過某些邊的最短路徑，可對應于貨車限行、外牌通行、規避事故等情形下的路徑規劃。

需要指出的是，以上這些應用場景和應用舉例與學生后續的專業核心課程密切相關。當然，針對不同專業的學生，需要增強應用舉例問題場景的針對性，以提高學生的代入感、認同感以及與后續專業課的銜接性，培養學生的完整知識體系。

在課后作業的設計方面，除了Dijkstra算法本身的鞏固練習外，我們也設計了最短路徑應用問題建模方面的作業。

（四）? 程序實現——綜合應用能力

我們在教學中引入“程序實現”環節，引導學生從程序設計角度進一步理解最短路徑問題的求解原理，同時增強學生學以致用、善用計算機工具的綜合能力。據筆者了解，在許多專業的課程安排中，運籌學的課程學習節點往往處在通識基礎課與專業核心課的銜接段，加入“程序實現”部分可更好地起到知識能力上的承前啟后作用，尤其是與計算機編程、數據結構、算法設計等前序課程的銜接，以幫助學生搭建更為完整的知識體系。

我們的課程作業設計如下。基于“程序實現”這個環節的教學設計，本教學團隊開設了運籌學實驗課。

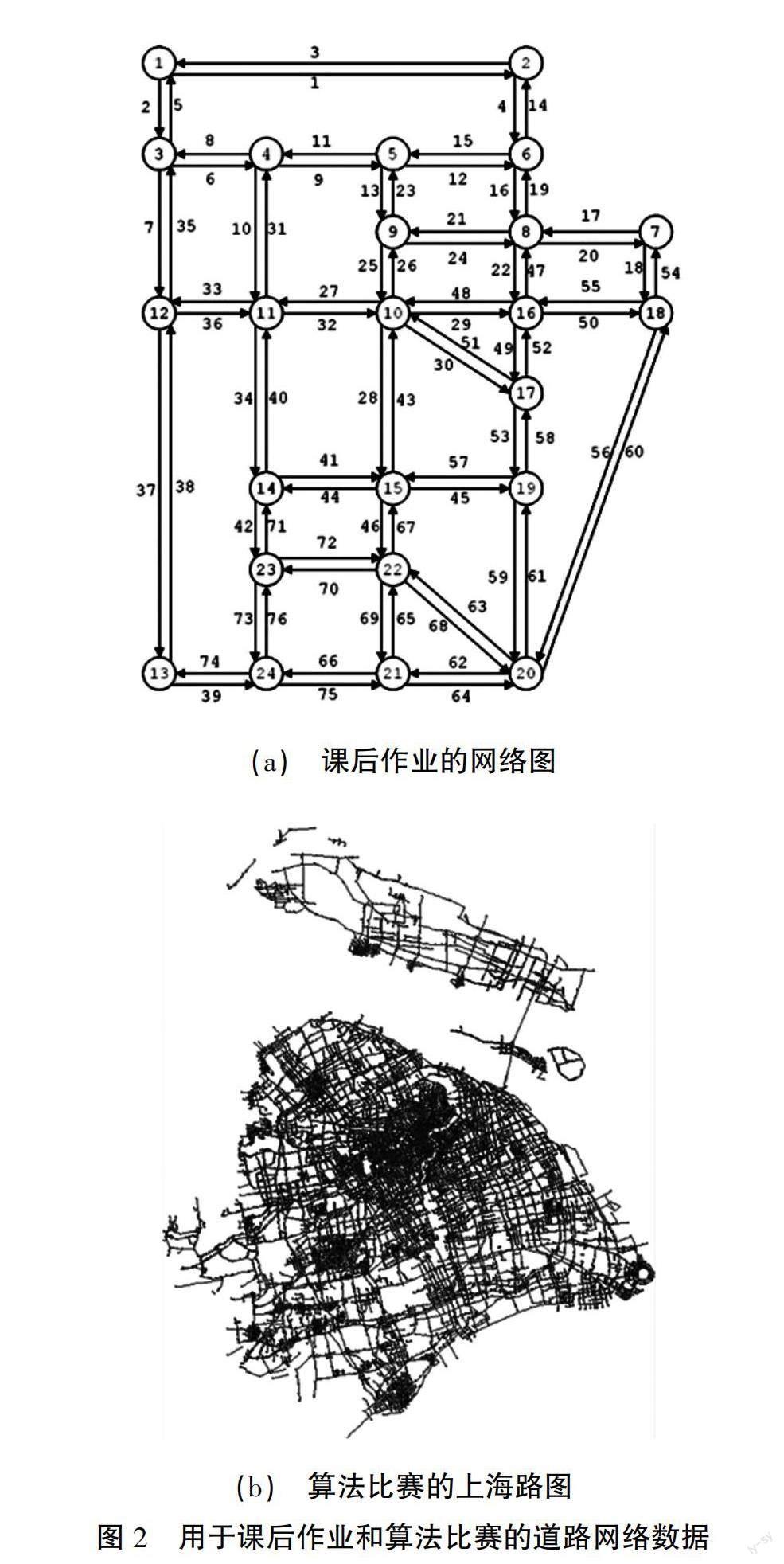
考慮如圖2（a）所示的網絡，該網絡包括24個頂點、76條邊。各條邊的編號、尾節點、頭節點、長度和容量如數據表所示。請編程完成如下計算。

1）計算所有頂點對之間的最短路徑長度，并采用合適的圖表形式予以表達。

2）計算每一頂點到其他各頂點之間最短路徑長度的平均值，采用合適的圖表形式予以表達，并討論該結果反映了網絡中哪些信息。

3）計算每條邊被最短路徑使用的次數，并按照該次數對所有邊進行排序，討論該結果反映了網絡中哪些信息。

該課程作業不僅考察學生程序設計是否可以計算出正確的結果，還啟發學生選擇合適的圖表形式對計算結果予以可視化，增強計算和分析結果的可讀性。其中，第3個任務引導學生挖掘最短路徑信息所蘊含的豐富應用價值。一般而言，出行者偏好最短路徑或綜合考慮多個準則的最優路徑。被多條最短路徑途經的邊，可能是交通網絡中比較關鍵的邊。若失效，會使得途經它們的多條最短路徑產生中斷，進而引發較為顯著的區域性、網絡化影響。

（五）? 算法比賽——團隊實戰積累

上述“程序實現”環節的測試網絡較小，對學生的要求是“算得準”；“算法比賽”環節的測試網絡采用學生們所在的上海市道路網絡（網絡拓撲如圖2（b）所示），網絡規模巨大（18 277個節點，41 199個邊），貼近現實，對學生的要求是提高“算得準+算得快”的實戰能力。

該算法比賽以2～3人的小組為單位，在相同的實驗室計算機硬件配置條件下，比較計算時間以及對計算結果的挖掘程度。要求不僅能夠較為高效地得出最短路徑計算結果，還需要進一步挖掘計算結果所蘊含的多種應用價值。

三? 結束語

針對現有最短路徑問題教學中存在的“被動接受、手工計算、只算不用”等問題，我們結合教學實際，根據“精選算法、縱向到底、橫向到邊”的教學理念，探索出“算法原理—數學建模—應用舉例—程序實現—算法比賽”五階遞進的最短路徑問題教學模式。2017—2022年的教學實踐結果表明，該教學模式有助于加深學生對最短路徑問題的理解認知，有利于提升學生的優雅學術品位與實踐創新能力，教學效果得到較大的提升。

在未來的運籌學教學中，對于網絡規劃中的其他經典問題，如最小生成樹、最大流、最小費用流等，均可根據問題自身特點與教學反饋，開展類似的多位一體教學設計，形成課堂內外雙向促進，以更豐富完整、有趣有效的教學設計，提升教學質量與學生綜合能力。此外，本文介紹的“應用舉例”主要針對我們授課的學生對象——交通工程和交通運輸類學生。針對不同專業的學生，可以引入相應的應用問題舉例，從而增強學生的專業意識，以及與后續專業課程的關聯度。

參考文獻：

[1] 傅家良.運籌學方法與模型[M].上海：復旦大學出版社，2014.

[2] 羅文昌.關于圖論教學的一些有益嘗試[J].大學數學，2014（30）：52-55.

[3] 李曉潔.基于問題導向教學的運籌學課程教學設計研究[J].高教學刊，2018（4）：101-107.

[4] 付云姍，劉蘭冬，劉奇鑫.關于運籌學教學方法的思考[J].科教文匯，2017（28）：40-41.

[5] 周喜華，胡振華，黃美銀，等.運籌學教學中融入數學建模實驗的研究和實踐[J].高教學刊，2017（11）：46-47.

[6] 姚翔飛，許鵬奎.教學研究型大學培養工科創新人才的實踐探索——基于學生創新能力提升的高校實踐教學體系改革與構建[J].長春理工大學學報，2010，5（7）：1-2.

[7] DEO N， PANG C Y. Shortest-path algorithms： Taxonomy and annotation[J]. Networks， 2010，14（2）：275-323.