基于出行者偏好特征的路徑誘導方法研究
李文勇,黎順虎,廉冠
(桂林電子科技大學 廣西智慧交通重點實驗室,廣西 桂林541004)
智能交通系統是人、車、路所組成的復雜人機系統,如何對出行者進行更均衡的路徑誘導是體現人機交互的熱點問題,出行者偏好特征時刻影響著駕駛員的路徑選擇行為。目前的路徑誘導方法考慮的因素過于單一,大多數都是在交通網絡中利用路段行程時間作為路段阻抗,從而尋找最優誘導路徑。但是由于出行者偏好特征的不同,其對各條路徑做出的判斷也會隨之改變,往往讓出行者很難做出合理的動態選擇,并不能與出行者偏好更好地結合,無法滿足多類型出行者的誘導出行要求。
Alder[1]基于虛擬路網分別通過路徑誘導和交通實時發布信息對駕駛員路徑選擇進行影響行為分析。James等[2]利用路徑選擇模塊和交通仿真模塊共同搭建系統框架,進而研究駕駛員在信息系統中的運行效率,研究結果表明,盲目提高或降低交通信息服務占有率,會給出行者路徑選擇帶來負面影響。高峰等[3]基于貝葉斯理論和多目標聯合決策理論構建路徑選擇模型。Hussein[4]在不同的誘導信息條件選擇傾向下,對出行者的路徑選擇進行研究,并構建了基于智能體方法的實時交通誘導信息影響下的出行者路徑選擇模型。Jou[5]深入研究了行程時間與出行距離等因素對出行者路徑選擇的影響,并由此構建了基于Probit模型的行程時間與出行距離聯合的路徑模型。Alexander[6]等為了讓誘導結果接近系統最優解,進一步探討了出行者的路徑選擇行為,重點分析總結了影響出行者路徑選擇行為的信息。張楊[7]以出行費用最小化為出發點,根據實時路網環境中出行者路徑選擇行為過程,構建了OD之間任意節點到終點的變分不等式模型,并給出了求解該目標模型的對角化嵌套算法。孫曉梅[8]主要研究多源交通信息下的出行者路徑選擇行為以及動態自適應路徑誘導選擇模型和算法。孫燕等[9]利用灰色系統理論建立尋路模型,且分析了出行者偏好對選擇結果的影響。劉智萍等[10]基于免疫遺傳優化提出了實時交通路徑誘導方法,通過對路徑評估、選擇的反復擇優,為出行者提供最優路徑選擇。
本文在以上研究方法的基礎上,提出了一種基于出行者偏好特征的多屬性決策路徑誘導方法。出行者主觀偏好能夠更全面地在路徑選擇方法中體現出來,通過對出行特性偏好調查分析獲取出行者偏好,用區間數的形式來表示目標路徑客觀屬性值,且指標屬性權重也在區間數的情況下,通過灰色關聯分析法判斷出行者主觀偏好與路徑客觀信息之間的綜合屬性值。利用基于偏好的遺傳算法進行求解,建立各個路徑間的可能度矩陣及排序向量,可以很好地為智能交通誘導系統提供選擇依據。
1 調查分析
綜合考慮影響駕駛員出行的選擇偏好,不同出行者對路徑屬性值有不同的心理側重程度。本文通過出行特性調查分析選取路徑選擇偏好指標,能夠充分反映駕駛員在日常出行中考慮的主要屬性。
本次問卷調查的主題對象是桂林市的居民,調查問卷主要來自現場調查以及網上問卷,回收填寫完整的問卷546份,得到有效問卷486份,問卷有效率為89%。
(1)出行者個人特征屬性
本文出行者個人特征屬性見表1。
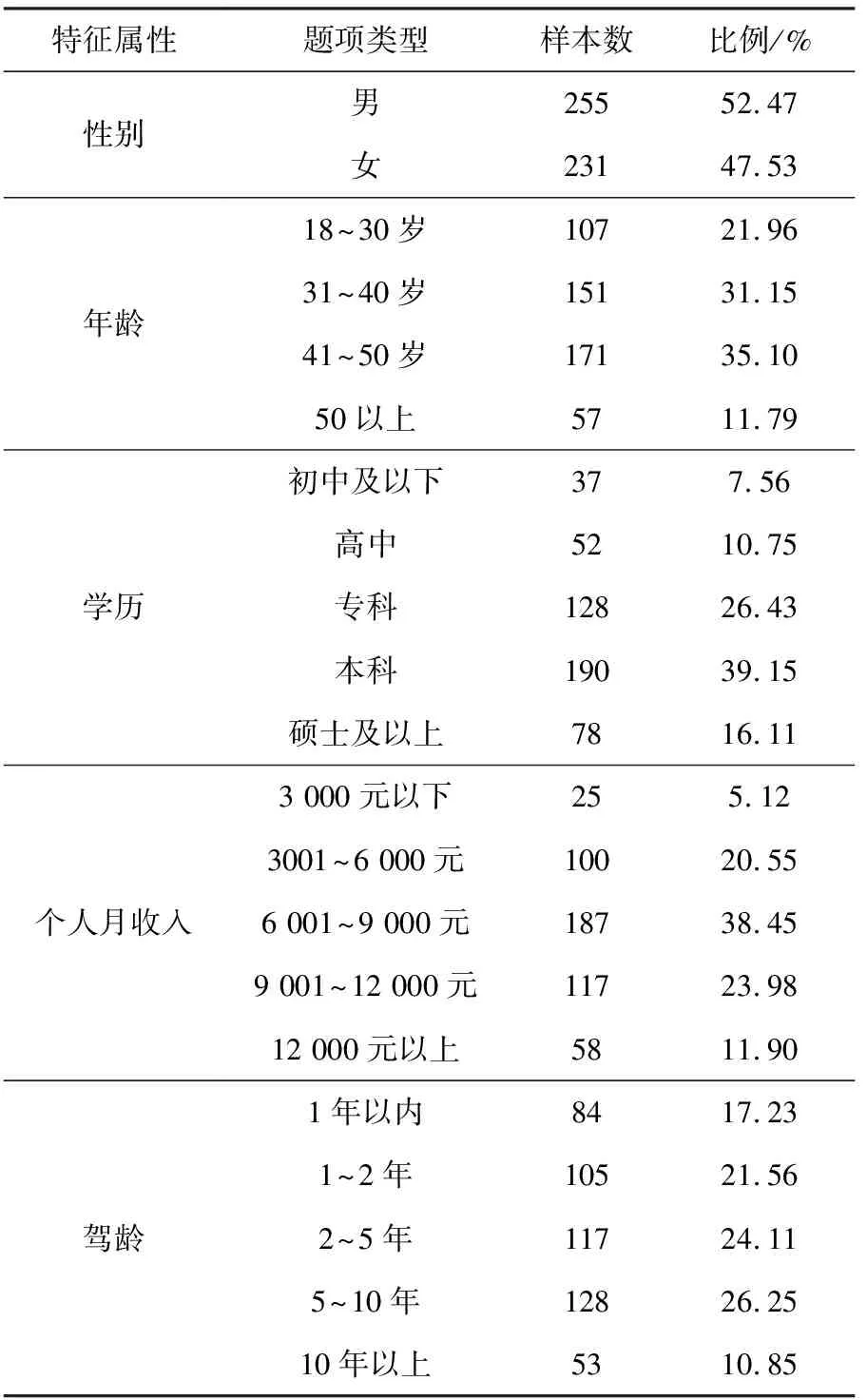
表1 出行者個人特征屬性
(2)出行者出行屬性信息
居民出行目的分布見表2。從駕駛員出行目的的分析結果可知,上班/上學的駕駛員所占比例達到了36.31%,其次為回家/探親(所占比例為29.75%),休閑/旅游、就醫分別為25.34%、8.6%。
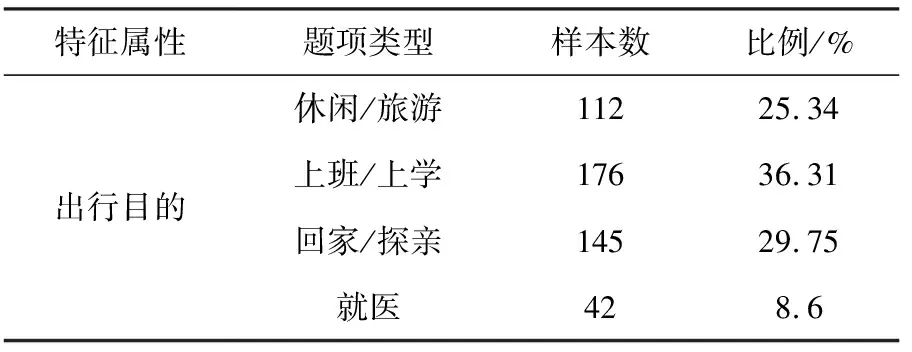
表2 出行目的分布
基于日常出行經歷,所選出行路徑屬性中行駛距離、行駛時間、擁擠程度、出行費用、轉彎次數、沿途景觀、信號燈數量、出行經驗、車輛組成成分、道路等級都影響出行者的決策,出行者選擇路徑方案主要偏好因素的重要度分析結果見圖1。
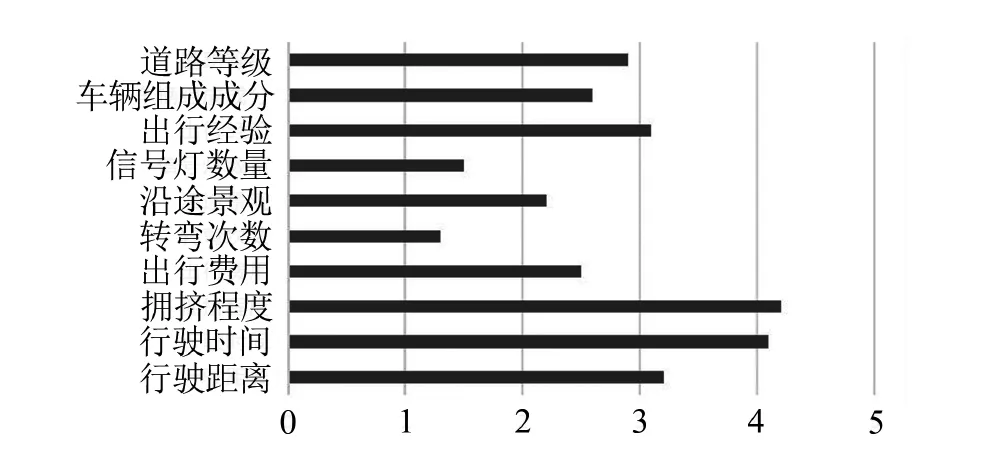
圖1 路徑主要偏好因素的重要度分析
由圖1可知,出行者選擇替代路徑主要因素重要度中,比較關心行駛時間、行駛距離、擁擠程度等屬性,其得分均超過3.2分。通過SPSS軟件對出行者路徑選擇行為與個人偏好之間進行相關度檢驗分析,得到偏好屬性顯著相異,后文建模將基于以上個人偏好因素進行。
本文首先對486條有效數據進行數據分析處理;其次對主要屬性進行描述性分析;最后對各個解釋變量(出行偏好因素)進行顯著性分析,以期為后續的路徑選擇模型解釋變量構建提供依據。
2 路徑選擇模型建立
考慮出行者偏好的路徑選擇問題目的是盡可能地減少路徑客觀屬性和出行者主觀偏好之間的偏差,本文的主要思路是把問題進一步轉化為求解關聯度問題,利用關聯度的解決方式求解。
2.1 路徑偏好目標描述
基于出行者對影響路徑選擇指標的行為偏好,本文以路徑信息作為客觀屬性值,將出行者的偏好特征作為主觀信息,進一步討論路網尋優問題。由于交通網絡存在很多不確定因素,出行者對各種主客觀信息的判斷不一,這就要求模型構建中要充分考慮出行者的主觀視角。本文以綜合建立考慮出行者偏好的路徑選擇模型,所建立的層次結構模型見圖2。
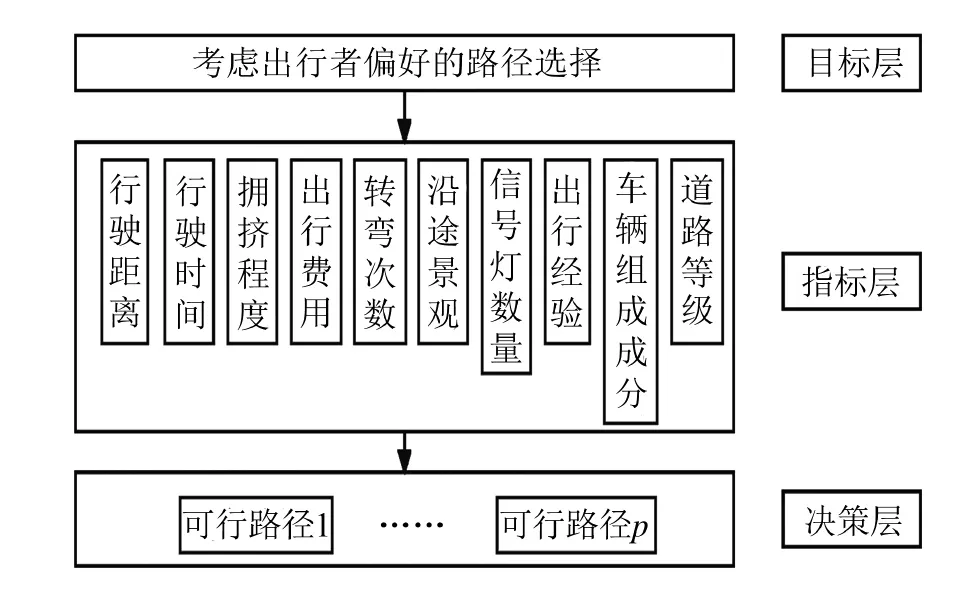
圖2 層次結構模型
2.2 灰色關聯分析法
灰色關聯分析法是灰色系統分析方法中的一種,能夠準確地依據各因素之間的相近的發展趨勢,權衡各因素之間的緊密程度。
(1)無量綱化處理
不同量綱造成各個指標的數據類型不同,為了消除不同變量不同量綱對決策的影響,對初始數據進行標準化處理。
(2)灰色關聯系數計算
根據層次結構模型選出各指標層的最優指標值,組成參考數列。決策層各個可行路徑的指標序列作為相對比較數列,由此計算各可行路徑中的指標序列與相對應的指標參考序列的關聯系數ξij。
(1)
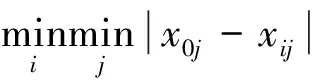
2.3 有偏好的路徑綜合屬性值計算模型
交通網絡中,起點Sq到終點Sz有m條可選路徑X1,X2,…,Xm(m≥2),出行者對任意一條路徑的選擇是由n個指標A1,A2,…,An決定的,每個指標An的屬性值為區間數,則原始決策矩陣可表示為:
(2)
為了消除不同量綱對出行路徑選擇決策的影響,對初始決策矩陣進行標準化處理。
對于效益性屬性:
(3)
對于成本性屬性:
(4)
規范處理后的決策矩陣記為:
(5)
標準化處理后的決策矩陣表示出行者對可選路徑的客觀屬性值。
出行者對可選路徑的偏好特征向量可以表示為θ=(θ1,θ2,…,θm),0≤θi≤1,i=1,2,…,m,由此計算可選路徑的客觀屬性值與出行者主觀偏好值之間的歐式距離:
(6)
由于交通網絡中多種條件的限制,為了滿足出行者主觀偏好路徑選擇特征,路徑指標權重向量w=(w1,w2,…,wn)應使可選路徑的客觀屬性值與出行者主觀偏好值之間的關聯度最大,為此建立如下指標權重最優模型:
(7)
由此關聯度最優模型求得指標權重,進而對主觀偏好值的綜合屬性值進行計算[11]。
各個路徑方案的綜合屬性值為:
(8)
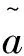
(9)
P=(Pij)n×n
(10)
其中:
(11)
對可能度矩陣P=(Pij)n×n采取排序向量求解:
(12)
由此得到排序向量v=(v1,v2,…,vn),按照vi的大小對可選路徑進行排序,vi越大則代表其對應的路徑更符合出行者的主觀偏好特征。
3 路徑選擇模型求解算法
多目標優化問題[12]中的每一個子目標往往是彼此沖突的,一個子目標的優化改善可能會引起其他子目標性能的降低,因此通常不存在一個絕對最優解可以使得所有子目標同時達到最優,只能通過在各子目標之間進行區間控制協調,使得其目標函數都盡可能地達到最優。本文在多目標優化問題中引入Pareto最優解的概念,而進行多目標優化問題求解的核心就在于獲得這些Pareto最優解所組成的集合。
本文將考慮出行者多個決策指標權重求解問題轉化為多目標優化問題,將各個指標轉化為目標子函數,問題描述為:
min{f1(X),f1(X),…,fn(X)}
s.t.i(X)≤0,i=1,2,…,m
(13)
式中:X表示決策指標;fi(X)表示目標關聯度;gi(X)表示指標權重的約束條件。
定義2 支配關系
求解多目標優化問題時,假如可行解X(1),X(2)∈XCon滿足以下關系:
(1)fi(X(1))≤fi(X(2)),即X(1)在所有目標函數上都不比X(2)差。
(2)X(1)至少有一個目標函數比X(2)的優,即在fi(X(1))≤fi(X(2))中至少有一個是嚴格不等式;則稱可行解X(1)支配可行解X(2)。
定義3 擁擠距離
設{a,b,c,d}4個解的rank相同,下面將兩個目標函數作為示例:
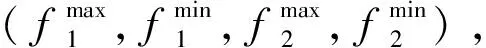
(2)對這4個解所得到的第一個子目標函數f1的值進行調整排序,由于f1的邊界為a,d,由此使得a,d的距離為∞,則b,c的距離為:
(14)
(15)
(3)再根據第2個子目標函數f2的函數值對這4個解進行排序,因為這4個解處于同一個rank上,所以它們的排列順序為{d,c,b,a},由此得出它們的擁擠距離分別為:
(16)
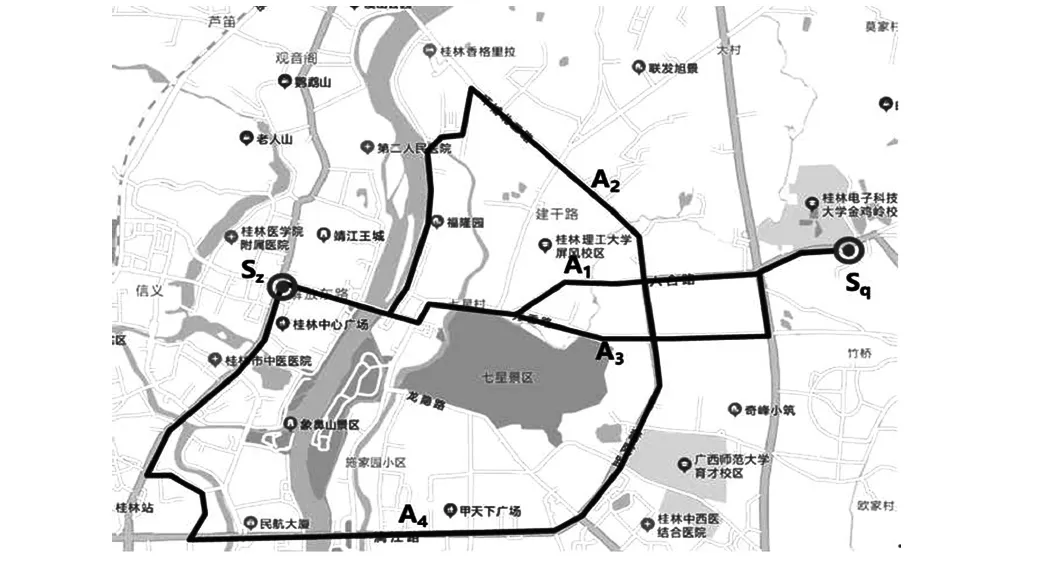
當個體的rank不同時,rank(i) Step 1 參數初始化:定義初始種群中個體數量NIND、運算迭代次數MAX-gen、變量個數VNIND、外部種群集合中個體數目OutNIND;創建初始種群Chrom以及外部種群集合OutChrom,設置代數gen=0。 Step 2 計算種群Chrom中各子目標函數f1、f2、…、fn的具體值,根據f1、f2、…、fn的具體值以及支配關系定義計算初始種群中每一個個體的階次值rank(i)以及擁擠距離。 Step 3 通過計算得到的階次值和擁堵距離對Chrom進行輪盤賭選擇,得到Chromparent,從而對Chromparent進行交叉變異操作,得到Offspring_Chrom。 Step 4 將Chrom和Offspring_Chrom進行合并得到下一代種群Chrom_1。 Step 5 判斷Chrom_1中的所有個體是否處于偏好區域內,將處于偏好區域內的個體放到外部種群集合OutChrom中,得到新的OutChrom。 Step 6 對Chrom_1以及OutChrom中的個體進行非支配排序得到rank、計算其擁擠距離。 Step 7 通過rank和擁擠距離對Chrom_1和OutChrom進行選擇,分別得到NIND個最優解的個體作為子代種群Chrom和OutNIND個數量的子代種群OutChrom。 Step8 gen=gen+1,若是gen≤maxgen,則跳轉到步驟3,否則結束循環。 基于偏好的多目標遺傳算法將進化過程中滿足偏好的個體都轉移到外部種群集合中,隨之根據階次值和擁擠距離對外部種群集合中的個體進行選擇,并且這些個體隨著遺傳尋優過程同時進行進化。此算法不僅能夠保證在整個目標空間內進行尋優,避免早熟現象,還能夠在特定的偏好區內產生Pareto最優解。 本文選取桂林市中心城區的交通網絡作為實例分析對象,見圖3。出行者從起點Sq到終點Sz,存在4條路徑可以選擇, 即路徑A1: 1→2→3→6→13; 路徑A2:1→2→3→10→11→12→13;路徑A3:1→2→4→5→6→13;路徑A4:1→2→4→5→7→8→9→13。將路網實例簡化為交通網絡,見圖4。 圖3 路網實例 圖4 交通網絡 考慮到出行者對可選路徑指標層各個屬性值的主觀偏好不同。本文將每個指標都通過區間數來表示,采用0~9表示出行者的不同主觀偏好值,例如行程時間為0表示時間成本最少,9表示時間成本最多。通過咨詢有桂林市區域出行經驗的專家,得到出行者給出的可選路徑的指標區間數,經過數據分析處理得到各路徑屬性的原始區間數,見表3。 表3 路徑各屬性區間數 求出路徑各屬性的權重也為區間數: 測定出行者對可選路徑各個因素的主觀偏好值:[0.3,0.5],[0.5,0.7],[0.3,0.6],[0.4,0.7],[0.4,0.5],[0.3,0.6],[0.2,0.5],[0.4,0.7],[0.4,0.6],[0.3,0.4]。 在這個多屬性路徑決策中,屬性類型分為成本型和效益型兩類,其中擁擠程度、行程時間、行程距離、出行費用、轉彎次數、信號燈數量、車輛組成成分為成本型屬性,沿途景觀、道路等級、出行經驗為效益型屬性。 規范化后的決策矩陣為: (17) 則可選路徑的客觀屬性值與出行者主觀偏好值之間的歐式距離為: (18) 計算各條路徑客觀屬性值對于主觀偏好值的灰色關聯系數為: (19) 則權重目標最優化模型為: (20) 由路徑求解算法解得路徑各屬性權重向量為: 由式(12)可得: (21) 將Pij代入式(13)得: v=(v1,v2,v3,v4)= (0.216 7,0.225 8,0.280 9,0.276 6) (22) 易見,v3≥v4≥v2≥v1。 可知v3對應的路徑為最優路徑,即路徑A3是最符合第k個駕駛員出行偏好的路徑。 由此可知,4條可選路徑的指標層屬性值均來自對桂林市中心城區路網比較熟悉的出行者,他們對桂林路網都具有豐富的出行經驗。出行者給出的可選路徑的指標屬性值能夠充分體現該區域路網的實際情況。利用本文提出的考慮出行者偏好的路徑選擇模型,對桂林市中心城區路網進行實例驗證,4條路徑的排序符合實際情況。 基于路徑誘導問題的多因素特點,進一步考慮出行者偏好和不確定性。本文提出了一種基于出行者偏好特征的多屬性決策路徑誘導方法,為出行者提供滿意度最高的路徑誘導建議。 (1)在出行者對影響路徑選擇有偏好的情況下,此方法能夠充分利用標準化評價的先行信息,較好地反映出行者對路徑各個因素的偏好側重點,盡可能滿足出行者的主觀偏好。 (2)基于偏好的遺傳算法,不僅能夠保證在整個目標種群內進行尋優、避免早熟現象,還能夠在特定的偏好區域產生最優解。 (3)智能交通系統是復雜的,出行者的偏好特征與交通網絡的實時狀態相互影響,如何將該方法動態的運用到智能交通誘導系統中,是下一步研究的重點內容。4 實例分析
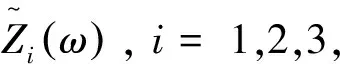
5 結論

