低滲砂巖油藏多孔介質特性
楊雪,劉建儀
(西南石油大學油氣藏地質及開發工程國家重點實驗室,成都 610500)
近年來,低滲砂巖油藏地位越來越重要,低滲油氣田在世界范圍內也非常豐富且分布廣,其中,北美、北歐、中亞、東亞和東南亞、北非等地區非常廣泛,隨著開采時間的延長,發現低滲復雜的油氣田比例越來越多。
國外關于研究多孔介質中流體運移機理常見的有達西定律,納維爾-斯托克斯方程,能量方程,哈根泊肅葉定律、伯努利方程、逾滲理論、有效介質理論、格子玻爾茲曼等;而自1975年美國數學家曼德勃羅創建了分形幾何,越來越多的學者開始研究其在多孔介質中的應用[1],探索復雜無序多孔介質中的有序化內在數學機理,分形理論在多孔介質輸運過程中的運用逐漸成為熱點[2],如Adler[3]研究了分形多孔介質在隨機地毯中縱向的斯托克斯流動,構造了由場地滲流推導出隨機截面的二維多孔介質,分析了分形多孔介質中的輸運,總結了連續確定性分形的構造方法、分維數和運輸的主要特征;Belyi等[4]認為分形多孔介質中光散射的蒙特卡羅模擬可用于分析光散射實驗數據和研究多孔介質結構,并研究了分形多孔介質裂縫的有效介質理論,多孔介質孔隙結構特征是決定流體微觀運移機制的重要方面。
中國關于分形理論運用于油氣藏開發方面的內容,郁伯銘[5]認為應用分形理論可解決有關多孔介質輸運領域的若干課題和方向且采用分形理論和方法對多孔介質滲透率和滲流機理能有深刻的認識和理解并描述了多孔介質中的輸運特性及實驗于計算機模擬方法;蔡建超等[6]利用分形理論描述了低滲透油藏的滲流力學規律,闡明滲流力學過程存在啟動壓力梯度的物理意義及滲流規律,并基于多孔介質中孔隙的分形特征,推導了含重力的濕潤液體在飽和氣體介質中自吸過程的完整解析模型,且研究了基于分形理論的低滲油藏若干輸運特性問題,如外來流體對低滲油藏介質的損害和低滲裂縫性油藏自發滲吸機理,從而降低儲層損害、提高采收率;王世芳等[7]建立了流體在分形多孔介質中滲流時的絕對滲透率及相對滲透率的分形滲透率模型,并與實驗及其他模型對比驗證。
中國石化中原油田礦場氣驅效果與方案設計預期效果相差較大,井況損壞頻繁、油藏能量不足等是導致注水開采困難,注氣驅油又發生氣竄等問題,缺乏多孔介質對輸運特性研究,而分形理論適用于從微觀尺度到宏觀尺度間的輸運特性研究[8-9]。針對上述問題,現展開低滲砂巖油藏多孔介質中微觀特征結構對輸運性質影響,以室內實驗為基礎,基于數學物理理論,利用計算機軟件,從更微觀的角度解釋和模擬多孔介質特征,為改善低滲砂巖開發效果提供技術支撐。
1 儲層特征
中國石化中原油田W區塊沙三組油藏位于東濮凹陷中央隆起帶北部衛東斷層下降盤,油藏埋深3 200~3 700 m,原始地層壓力34.50 MPa,原始地層溫度114 ℃,平均滲透率2.25 mD,平均孔隙度12.70%,飽和壓力22.64 MPa,地層原油黏度 0.284 MPa·s,原始氣油比159.64 m3/m3,地層原油密度0.702 5 g/cm3,地面原油密度0.872 9 g/cm3,原油體積系數1.533 7 m3/m3,地層油平均溶解氣體系數為7.198 (m3/m3)/MPa,井流物中 C1含量61.115%,中間烴(C2~C6)含量32.372%,C7+含量2.605%,凝固點33 ℃,脫氣油相對分子質量為276.4,地層水礦化度為27.70×104mg/L,水型為CaCl2,屬于低孔低滲油藏。
2 實驗方法
2.1 鑄體薄片圖像分析
目前中國石化中原油田低滲砂巖油藏采取注氣提高采收率,通過對目標區塊的多孔介質孔隙特征進行鑄體薄片圖像實驗,獲得一些相關基礎數據,為后期多孔介質分維數計算提供數據支撐。孔隙結構基本特征參數值公式[10-13]為

(1)
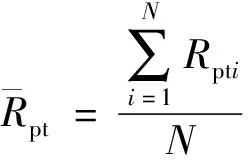
(2)

(3)

2.2 壓汞曲線
用恒速壓汞技術以恒定極低的速度注入巖心中,產生一個進汞壓力降落,得到孔隙和吼道的毛管壓力曲線[14]。該方法主要涉及參數如下。
毛管壓力與孔徑間的關系為
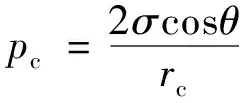
(4)
式(4)中:pc為毛管壓力,MPa;σ為表面張力,N/m;θ為潤濕接觸角,(°);rc為毛管半徑,μm。
汞飽和度為
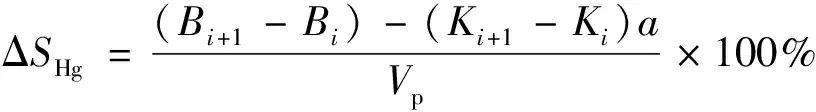
(5)
SHg=∑ΔSHg
(6)
式中:ΔSHg為汞飽和度增量,%;α為儀器的體積常數;Bi、Bi+1分別為壓力pi、pi+1時的進汞量,mL;Ki、Ki+1分別為壓力pi、pi+1時,空白實驗體積的測量值,mL;Vp為孔隙體積,mL;SHg為累積汞飽和度,%。
退泵效率為
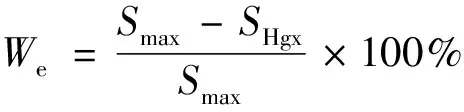
(7)
式(7)中:We為退汞效率,%;Smax為最大進汞飽和度,%;SHgx為殘余汞飽和度,%。
2.3 分維數計算
W區塊屬于低孔低滲砂巖油藏,實際作業和驅替過程中,儲層結構會發生隨機、不穩定、不可逆的非線性變化,使得油氣滲流處于無序、非平衡狀態之中,但再復雜的現象背后,總存在著某種規律。分形多孔介質通過分維數預測儲層巖石孔、滲等參數非均質分布,常見的分維數有豪斯道夫維數、盒維數、信息維數、關聯維數、相似維數等,其中,盒維數是應用最廣泛的分維數之一。
盒數法的確定,從信息學的角度,可用幾種輸入類型描述Rn的子集;從數學角度,盒維數的定義如下[15-16]:設A是Rn空間的任意非空有界子集,對于任意的r>0,Nr(A)表示用來覆蓋A所需邊長為r的n維立方體(盒子)的最小數目,如果存在一個數DB,使得當r→0時,有
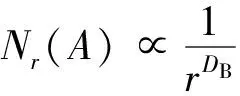
(8)
式(8)中:DB為A的盒維數,無量綱;Nr(A)為A的盒數量;r為盒的邊長。
當且僅當存在一個正數k時,有

(9)
式(9)中兩邊為正,均取自然對數,得
(10)
進一步得

(11)
因lnk是常數項舍去。當r→0時,分母趨于無窮大,由于0 使用Frac Lab和Frac Lac兩個分形軟件進行計算盒維數,其中Frac Lab是基于分形和多重分形方法的信號和圖像處理軟件,用plain box方法計算盒維數;Frac Lac為ImageJ軟件中的一個插件,主要用于盒維數、質量維數的計算。 低滲油藏的多孔介質中孔隙分布非常復雜,通過鑄體薄片、壓汞實驗和分形的計算,得出以下結論。 多孔介質的孔隙結構直接影響巖石滲流特性,W區塊儲層巖性主要為石英粉砂巖、細砂巖,砂巖碎屑主要為石英80.6%、長石13%、巖屑7.4%,分選差,膠結物以泥質、方解石為主,為點接觸,膠結類型以孔隙式為主。儲層物性在平面上、縱向上都表現出非均質性。為研究巖石孔隙大小、分布及幾何形態、平均孔喉比、配位數等進行了鑄體薄片圖像實驗,如圖1所示。 該區塊薄片圖像可直觀地理解孔隙間的連通性,經分析可知:該區塊的巖石致密,雜基豐富,壓實明顯,孔隙較難注入且注入不均,局部細微或零星分布,平均孔隙直徑30.64 μm,平均喉道值 3.08 μm,平均配位數0.03,平均孔喉比0.31,分選系數14.93,均質系數0.38。 毛管壓力曲線如圖2所示,滲透率貢獻與汞飽和度分布頻率關系曲線如圖3所示。 圖2 毛管壓力曲線 圖3 汞飽和度和滲透率貢獻曲線 由圖2可知:右邊為進汞曲線,最右邊垂直于X軸的部分無進汞飽和度,說明無大孔道;中間平滑段進汞效率較高,表明在0.294~0.735 MPa進汞效率高達近50%;最上面進汞效率,當毛管壓力成指數上升時,僅進汞25%左右。左邊退汞曲線,從曲線上看退汞效率為21.8%,說明無大孔道,微毛細管多。 由圖3可知:毛管半徑主要集中在0.006~2.5 μm 范圍內,對滲透率有貢獻的毛管分布在0.16~2.5 μm,對滲透率貢獻最大的毛管半徑為2.5 μm,貢獻率達70.3%,但分布頻率卻不是最高的,說明占據數量最多的毛管對滲透率的貢獻卻未達到最大。微小孔隙占比較重,喉道較窄,且數量少,孔隙結構較復雜,儲層滲流能力弱,滲流阻力大,增加開采難度。 本文研究使用的是灰度圖像輸入類型,亮點像素被視為峰值,暗像素被視為谷值。首先輸入W區塊的鑄體薄片圖像,對圖像進行邊緣檢測、灰度處理,如圖4所示,將覆蓋區域內的盒維數數量與尺度對應,尺度大小以冪律標準歸一化處理后,基于最小二乘法進行擬合計算,最后,輸出選定區域曲線雙對數,斜率為該圖像的分維數。 圖4 Fra lab軟件處理的灰度圖 通過Fra lab盒維數評估:尺度呈指數分布,最小二乘回歸分析后擬合曲線得尺度和盒數量對數函數線性關系曲線,結果:評估的盒維數為2.58,相關系數為1,振幅為 0.93%。 分維數值在一定尺度范圍內才具有分形幾何意義,一般值在0~3[17],研究發現多孔介質分維數值越小,結構越松散均質[18];反之,孔隙內結構復雜致密,微小孔隙多,非均質性嚴重,這種情況,不利于油氣開采。 分形物體的量度M(ε)與測量尺度ε關系是分形幾何的一個基本式,即 M(ε)∝εDB (12) 式(12)中:M為分形物體的量度;DB為盒維數;ε為測量尺度。 DB主要根據某種模式,測量物組成數量(N)和測量尺度(ε)間的關系推斷,為一種標度規則,即 N=ε-DB (13) 對數求解方程中的DB,得 (14) 灰度圖像的盒維數為假定存在于擬3維空間中,像素從0到255,提供一種3維空間測量紋理,并讓灰度值(強度)代表體積。將屏幕想象成一個有i行和j列的二維網格,位于(i,j)的每個像素在3維空間中就像小棱鏡一樣向上到由強度定義的相對高度,Frac Lac將這種體積空間轉化為盒維數的強度差,通過對多個盒子尺寸進行多次測量,根據數據回歸線的斜率近似雙對數關系推斷一個比例規則,可確定2種不同類型的盒維數:DB取自所有I(i,j,ε)之和相對ε的雙對數回歸線;DM取自所有I(i,j,ε)平均值相對ε的雙對數回歸線。 灰度圖像的三維體積V(i,j,ε),其將取決于盒子大小、形狀及強度范圍,Frac Lac計算近似體積為 V(i,j,ε)∝I(i,j,ε)ε2 (15) Frac Lac計算V(ε)相對ε的雙對數斜率后,用一種基于半變異函數法計算盒維數DB,即 V(ε)=∑I(i,j,ε)ε2 (16) (17) (18) 式中:I為強度;i為樣品;ε為尺寸大小;S為回歸線斜率。 質量維數DM方程為 (19) 多孔介質中,實際注入的流體在孔道中的流動,存在一定的隨機性,分維數反映復雜形體占空間的有效性,其值與孔隙結構的非均質性一致。 對孔隙結構進行盒維數評估,通過Frac Lac分形分析軟件模擬計算,得到W區塊盒維數DB和質量維數DM。 圖5 平均強度的雙對數曲線V(ε)的斜率相對ε (1)以中國石化中原油田W區塊低滲巖樣為例,將室內基礎實驗和分形分析軟件相結合,進行巖樣孔隙特征分析,發現該區塊的巖石致密,雜基豐富,孔隙結構復雜,非均質性嚴重,微小孔隙多,孔隙壁面粗糙,滲流阻力大,油氣開采的難度較大。 (2)以最簡單的分形理論方式表征多孔介質的微觀結構特性,利用分形分析軟件Frac Lab和Frac Lac模擬計算了W區塊多孔介質分維數值約為2.58,與室內微觀結構試驗結果具有良好的一致性,定量化反映了該區塊多孔介質復雜形體的不規則性,結果表明:該區塊孔隙結構較復雜,壁面粗糙不利于滲流,開采難度大。 (3)將Frac Lac軟件應用在油氣開發中,并與Frac Lab軟件進行比較,評估多孔介質分維數。為中國石化中原油田低滲透油藏多孔介質中油氣運移規律研究、開發潛力評價和方案制定提供了基礎數據支持,對油田開發具有重要的現實意義。3 結果與討論
3.1 鑄體薄片
3.2 壓汞曲線
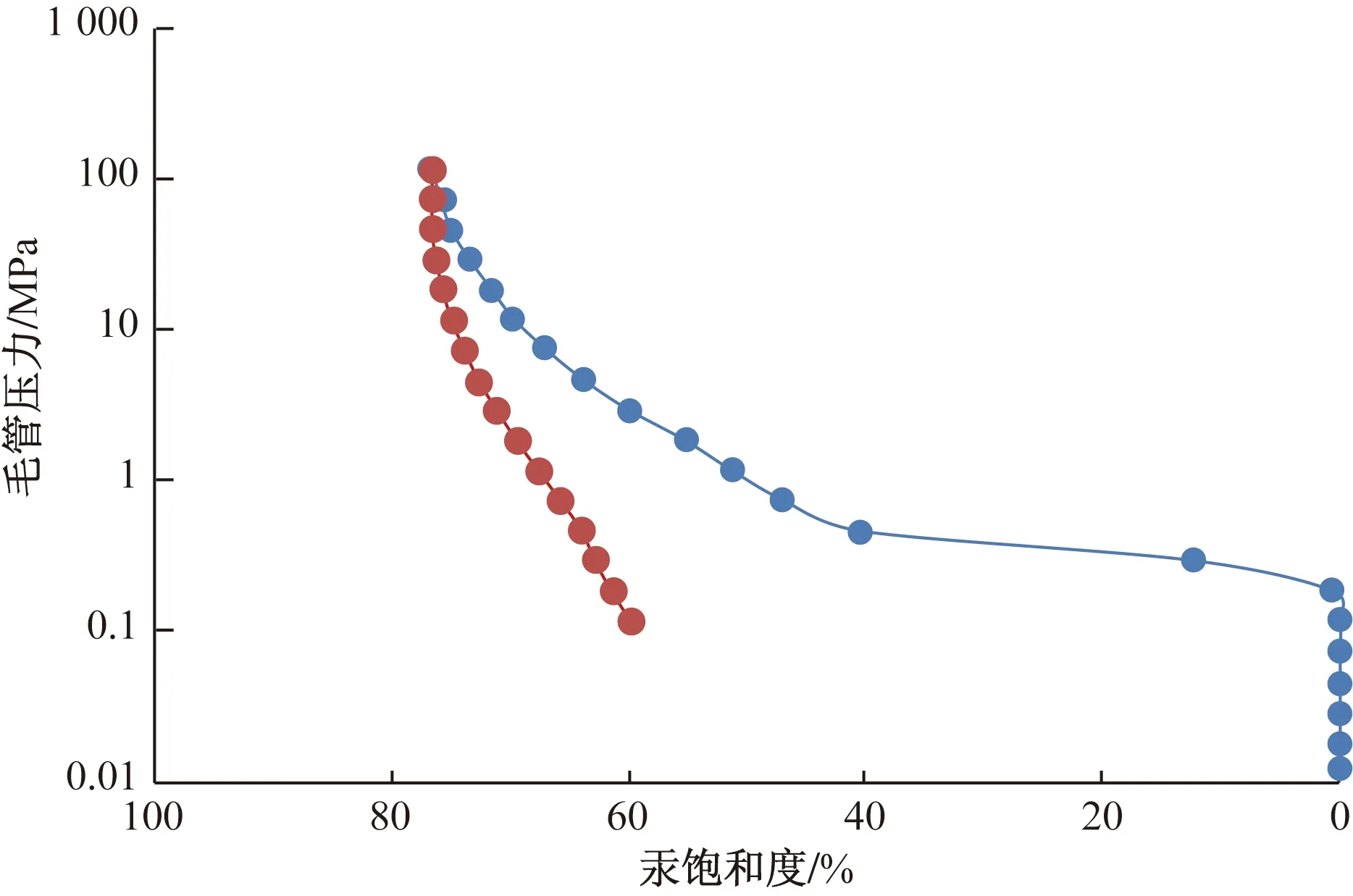

3.3 Frac Lab計算盒維數

3.4 Frac Lac計算盒維數
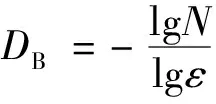

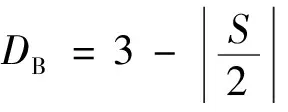
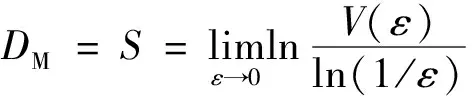
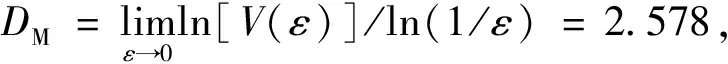
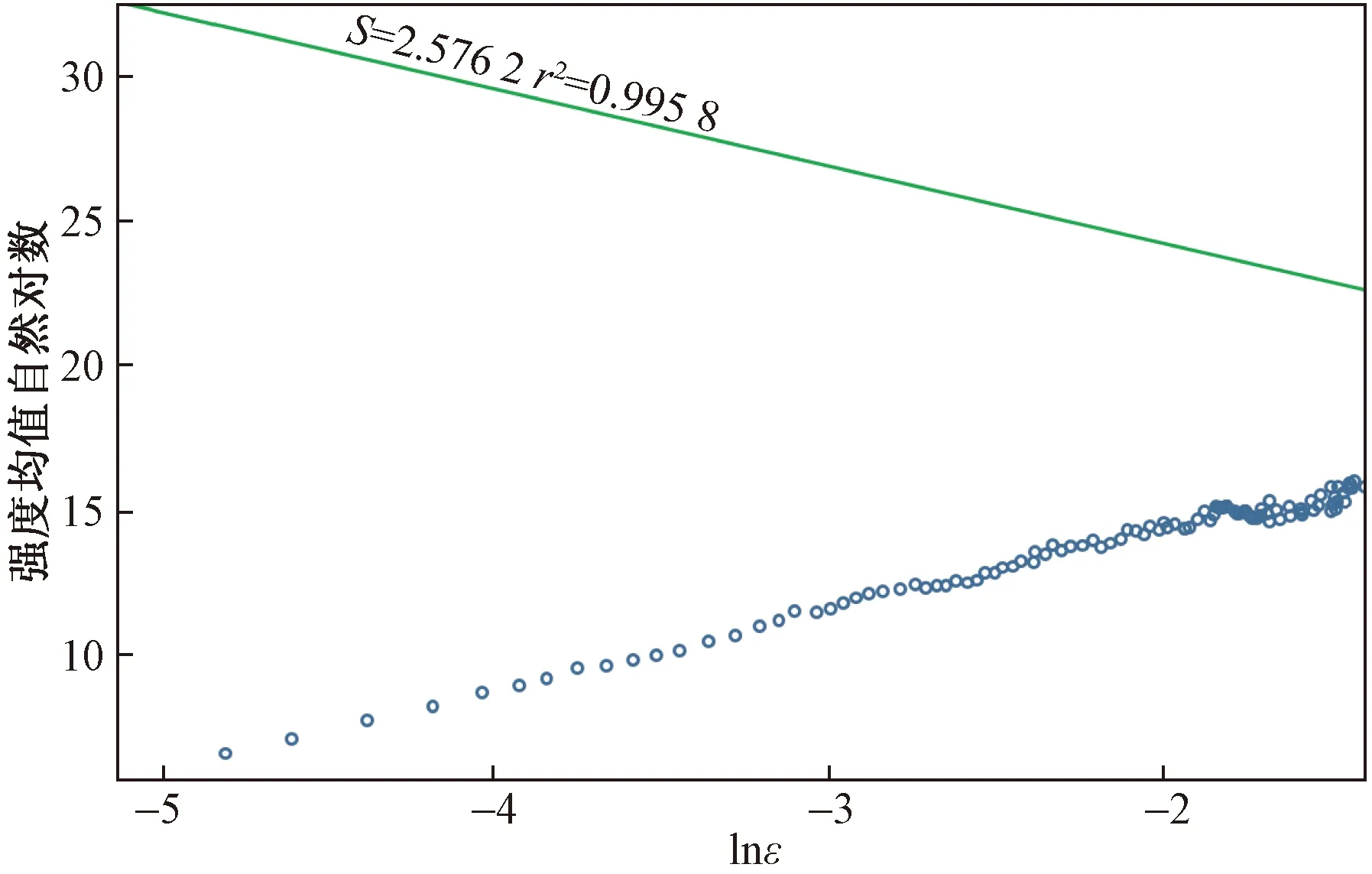
4 結論

