冰風耦合環境下連接金具數值仿真分析

路國闖,李新梅,商利,楊現臣,王曉輝

(新疆大學機械工程學院,烏魯木齊 830000)

受大風、冰雪天氣影響,輸電線路連接金具在遠低于其服役年限下就發生了失效斷裂[1]。輸電導線作為一類大跨高柔結構,易受風荷載影響,產生一種低頻、大幅自激振動。風致振動引起的動張力作用在金具上,伴隨著碰撞與扭轉,極易使金具連接處出現斷裂和變形[2-4],輸電線路覆冰后,導線內部張力變化加劇,金具接觸區應力激增,進一步加快了金具失效。

輸電線路長期暴露在戶外工作,常受大風、沙塵暴、酸雨、冰雪等惡劣環境影響,因此,中外對電力金具的研究主要是圍繞不同介質環境下金具失效分析,采用試驗或有限元或兩者相結合的方法對金具失效過程中的易損位置進行觀察與模擬。楊現臣等[5]、王曉輝等[6]針對新疆大風區U形掛環磨損行為進行研究,通過試驗得到施加載荷、磨損次數和擺動頻率對剩余尺寸的影響,通過對表面形貌和力學性能的檢測,闡述了大風環境下U形環的失效機理;陳軍君等[7]針對工業大氣環境下金具腐蝕進行研究,通過一系列實驗并分析發現S元素是促進金具腐蝕速率的關鍵。然而上述研究都只是對單一工況下金具的失效分析,隨著研究的深入,不少研究者發現,多工況的交織影響對金具損傷起到疊加和加速作用,也更加符合實際。Wang等[8]利用FLUENT對風沙場進行數值模擬,考慮沙粒侵入影響,得出沙粒對U形環磨損失效起到促進作用的結論;張培軍等[9]通過實驗模擬外界真實大氣環境下金具腐蝕與磨損的交互影響,得到預腐蝕磨損后的質量損失要比純磨損增幅最大達到22%。導線在復雜工況下極易產生振動并具有多變性,因導線不停振動在金具受力點產生的交變的彎曲應力也具有不可預測性,因此,針對單一金具局部失效分析存在一定的局限性。文獻[10-12]通過建立整體輸電線路模型,采用有限元法模擬風荷載作用下導線振動引起的附加應力對連接金具的影響,得到金具的易損位置和破壞機理;周曉慧[13]在整體輸電線路模型的基礎上考慮導線檔距和高差角對金具受力的影響,為線路金具的優化提供了理論參考。但在對輸電線路連接金具模擬中,均缺乏對局部金具運動形式的考慮且只是針對單一大風工況,對復雜工況下的金具失效分析適用性存在一定的局限性。

現對冰風耦合作用下導線關鍵點處運動軌跡和張力變化進行研究,并考慮導線覆冰形式的影響,對最大載荷工況下整體連接金具應力情況進行分析,并針對危險部件U形環進行動力響應分析,對比轉動關系對金具的影響,提高輸電線路抵御冰風聯合振動造成損傷的能力,確保在復雜環境下,線路能夠安穩的運行。

1 冰風荷載下導線關鍵點位移和動張力計算

1.1 線路參數

考慮冰風耦合效應,對某220 kV輸電線路振動響應進行數值模擬,幾何參數如圖1所示。導線及連接金具參數分別列于表1和表2中。

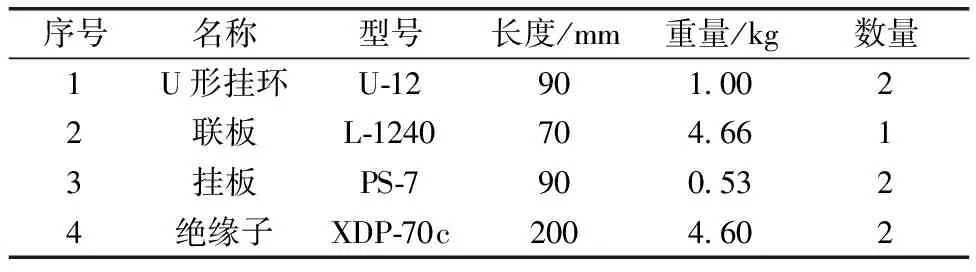
表1 連接金具物理參數

表2 導線物理參數

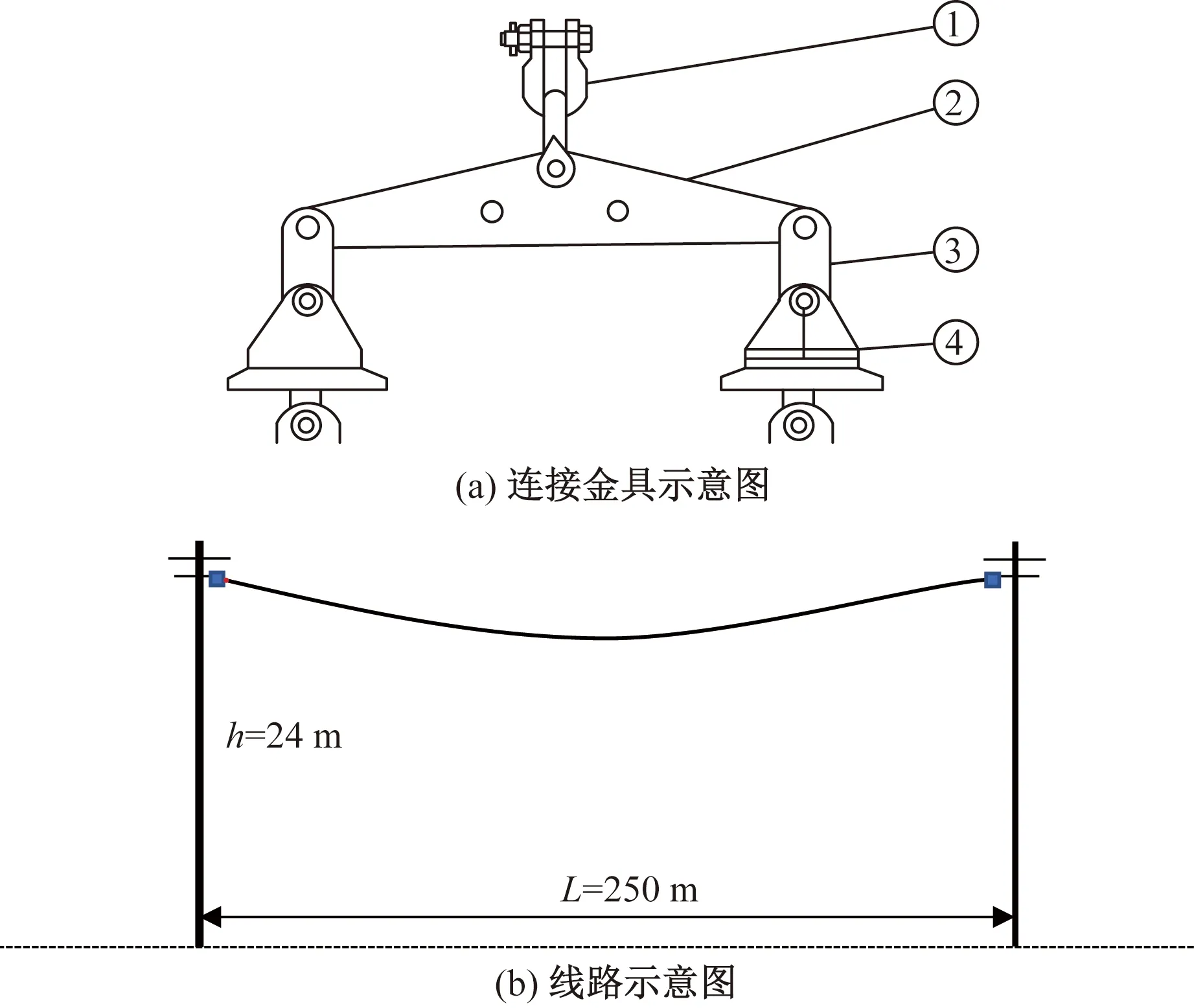
L為檔距;h為桿塔呼高

1.2 導線振動響應仿真

在對導線振動特性仿真前,首先對風荷載進行數值模擬。自然風包括平均風和脈動風,根據線路所處區域地貌特點,基于指數公式求得節點平均風速。采用隨高度變化得Kaimal風速譜[14],并考慮Davenport空間相關性[15],基于諧波疊加法獲得導線各節點脈動風速。根據中國《線路規范》風荷載標準值計算公式求出作用在導線上的水平風荷載[16]。

輸電導線在無外部載荷作用下只承受沿弧長均勻分布的自重載荷,初始狀態為懸鏈線,表達式[17]為

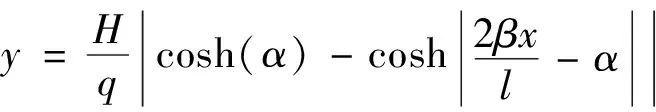
(1)

式(1)中:

為初始水平張力;q為作用在導線上的均布力。

輸電導線覆冰后改變了導線的初始位形,采用附加冰單元法[18],即

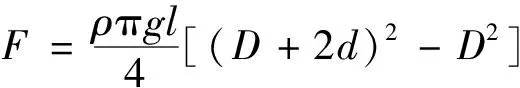
(2)

式(2)中:F為導線長度l覆冰重量,N;ρ為900 kg/m3;D為導線外徑,mm;g為重力加速度,取9.8 m/s2;d為覆冰厚度,mm。

通過作用在導線節點上的集中力模擬輸電導線均勻覆冰以及線性覆冰工況,均勻覆冰時,覆冰厚度分別取5、10、15 mm;現實生活中大多為線性覆冰,為簡便計算,將輸電導線均分為3段,相同高度處覆冰厚度相同,分別模擬輸電導線兩側重覆冰和中央重覆冰,為了更好地與均勻覆冰進行對照,薄覆冰取為5 mm,厚覆冰為15 mm,如圖2所示,覆冰類型為圓形截面。

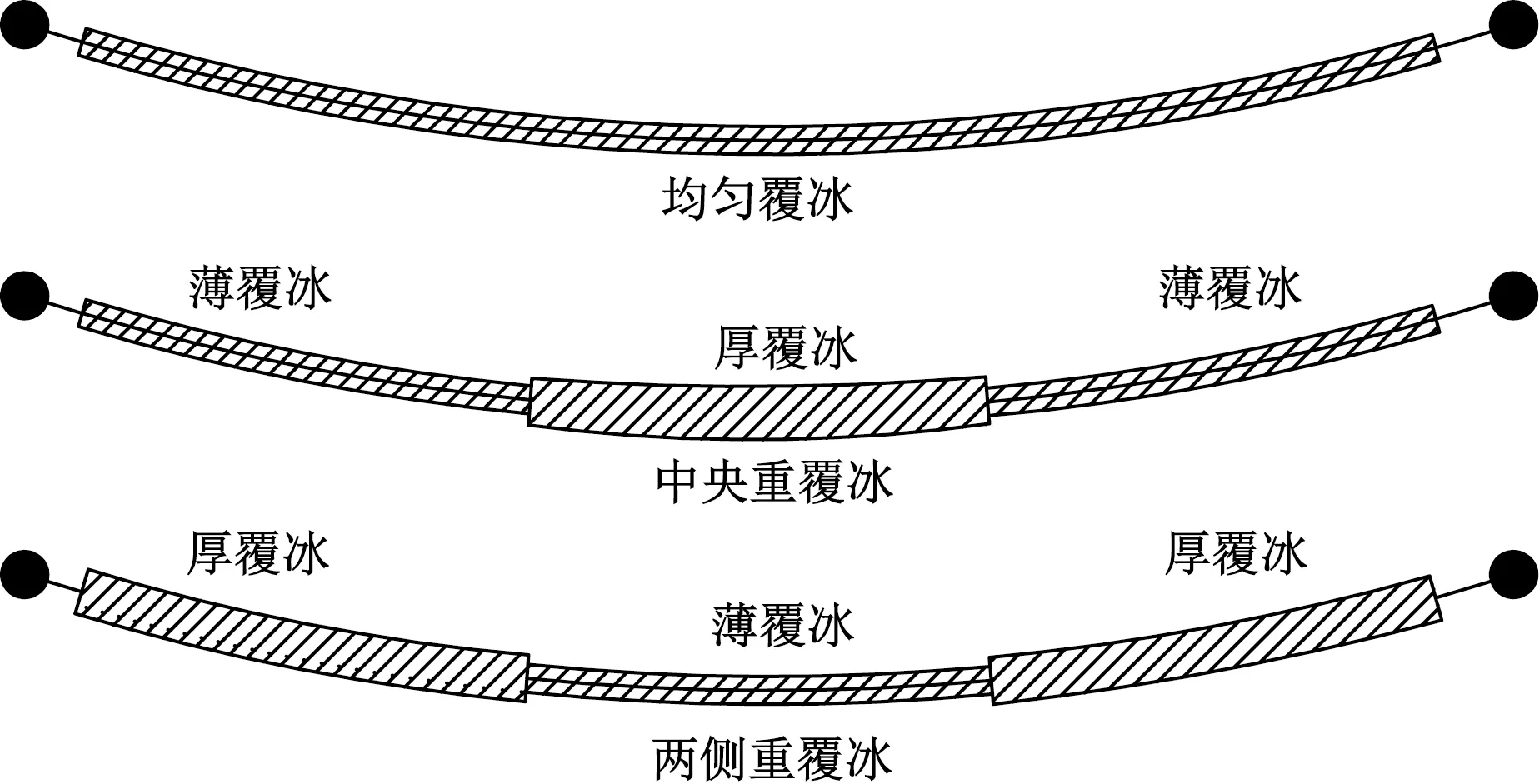
圖2 覆冰示意圖

導線受到順風向風載,考慮慣性力和阻尼的作用,進行瞬態動力學分析,非線性運動方程為

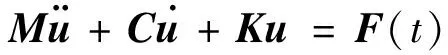
(3)

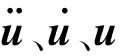
基于導線有限元模型,如圖3所示,在ANSYS中采用完整矩陣,考慮各類非線性,采用瑞利阻尼,使用Newmark時間積分法對方程進行求解。

1.3 仿真結果分析

在隨機風的作用下,覆冰導線不僅受到水平方向的強迫振動,在豎直方向也會產生振動,本文研究選定離地面高度10 m處基準風速為15 m/s,對100 s內不同覆冰狀態下導線關鍵點位移進行數值計算,提取結果文件并繪制軌跡圖,如圖4所示。可以發現,在風荷載作用下,關鍵點處運動軌跡主要呈橢圓形狀。均勻覆冰時,導線豎向位移(Y向)隨著冰層厚度的增大而降低,在覆冰15 mm時達到最低;不均勻覆冰時,導線豎向位移相近。受水平風荷載的作用,關鍵點的順風向(Z向)位移主要集中在Z軸正向,與實際觀測導線振動軌跡相符。

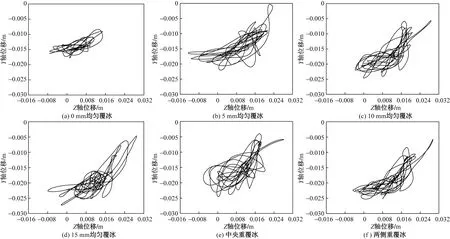
圖4 不同覆冰形式導線關鍵點運動軌跡

提取作用在金具上的動張力,在軟件中通過編程語言提取導線關鍵節點軸力變化,并繪制張力時程曲線,如圖5所示。可以發現,在均勻覆冰15 mm時,有最大張力值為71 800 N,選用該值作為后續整體連接金具靜力分析輸入荷載。

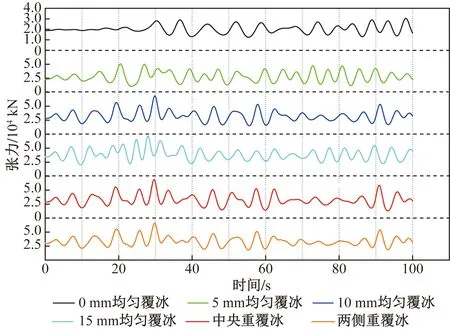
圖5 不同覆冰形式導線關鍵點動張力時程

2 連接金具力學模型和有限元模型建立

2.1 力學模型

在輸電線路實際運行中,連接金具受力復雜包括:線張力,冰重力以及風荷載[19]。本文研究針對力作用下金具運動狀態建立簡易力學模型,如圖6所示。

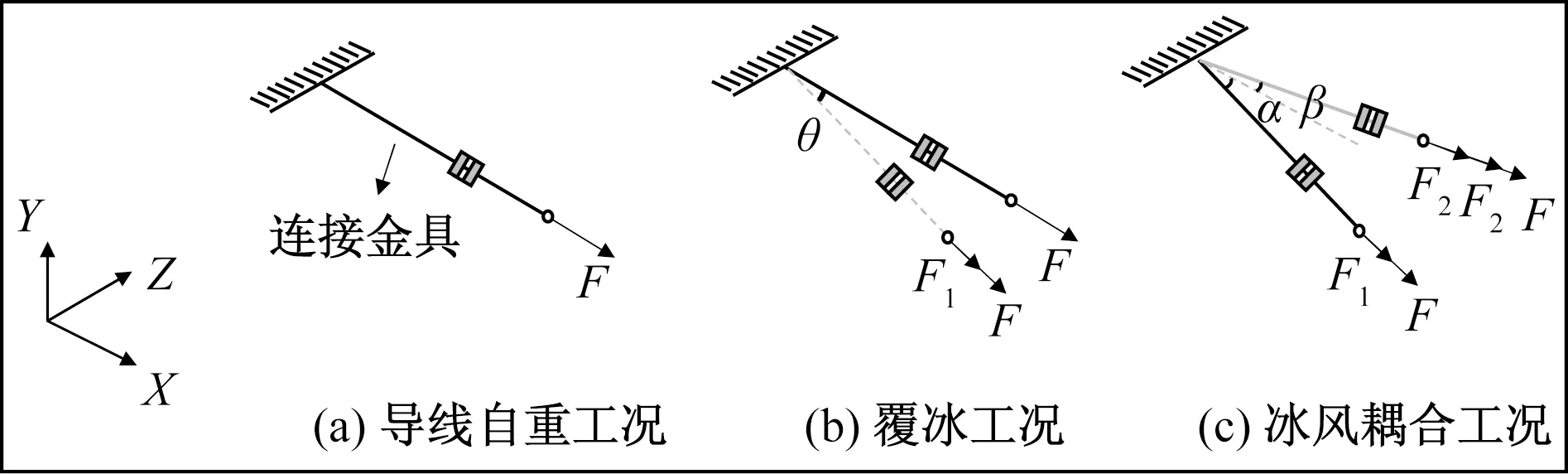
F為連接金具與導線連接處的張力值;F1為覆冰工況下張力增量;F2為風荷載作用下張力變化大小;θ為冰載作用下連接金具擺動角度;α、β分別為冰風耦合下金具面外轉角和面內轉角

2.2 有限元模型

為真實反映連接金具受力狀況,等比例建立U形掛環、聯板、掛板、螺栓等幾何模型,并根據連接狀況進行約束裝配,如圖7所示。考慮金具材料非線性和幾何非線性,采用雙線性等向強化模型來表征材料的應力-應變關系,打開大變形開關,實時更新結構剛度矩陣。通過在U形環內孔表面施加固定約束和掛板內孔表面施加軸承載荷(bearing load),近似表示U形環和桿塔的緊固連接以及連接金具所受載荷,載荷大小為關鍵點處最大動張力值,如圖8所示。

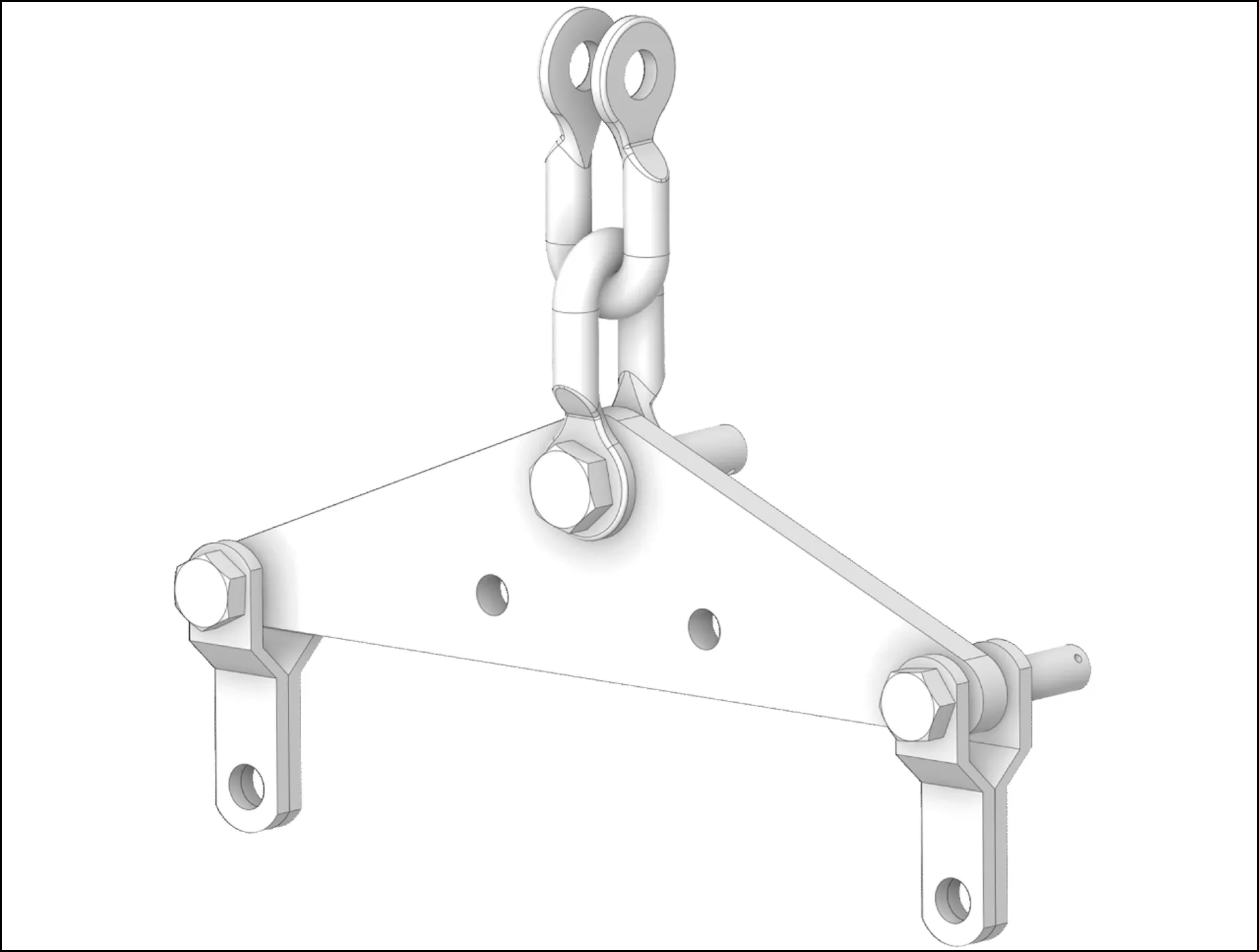
圖7 連接金具有限元模型裝配圖

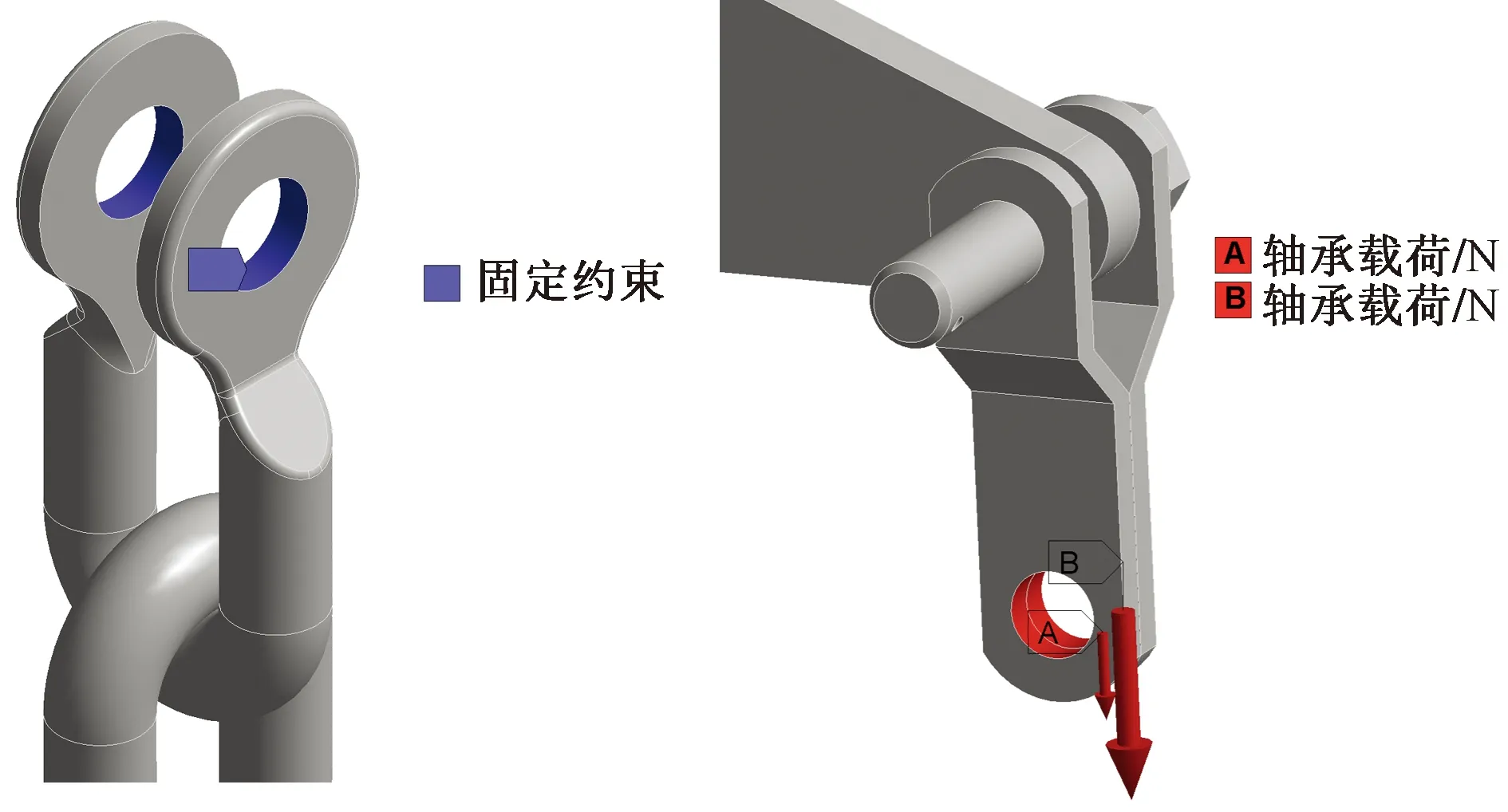
圖8 邊界條件

在輸電線路實際運行中,U形掛環受力復雜,在外力作用下還會出現轉動發生磨損失效現象,為了精確描述接觸區域的應力變化,找出易損部位,單獨建立簡易U形掛環模型進行動力學分析,考慮U形環的轉動自由度,接觸類型選用Frictional,摩擦系數設為0.3。對上U形環施加固定端約束,在下U形環端面施加法向荷載,通過三角函數將導線關鍵點處路徑轉化為U形環Y、Z方向的轉動角度,通過遠端位移約束(remote displacement)施加在接觸區域,如圖9所示。

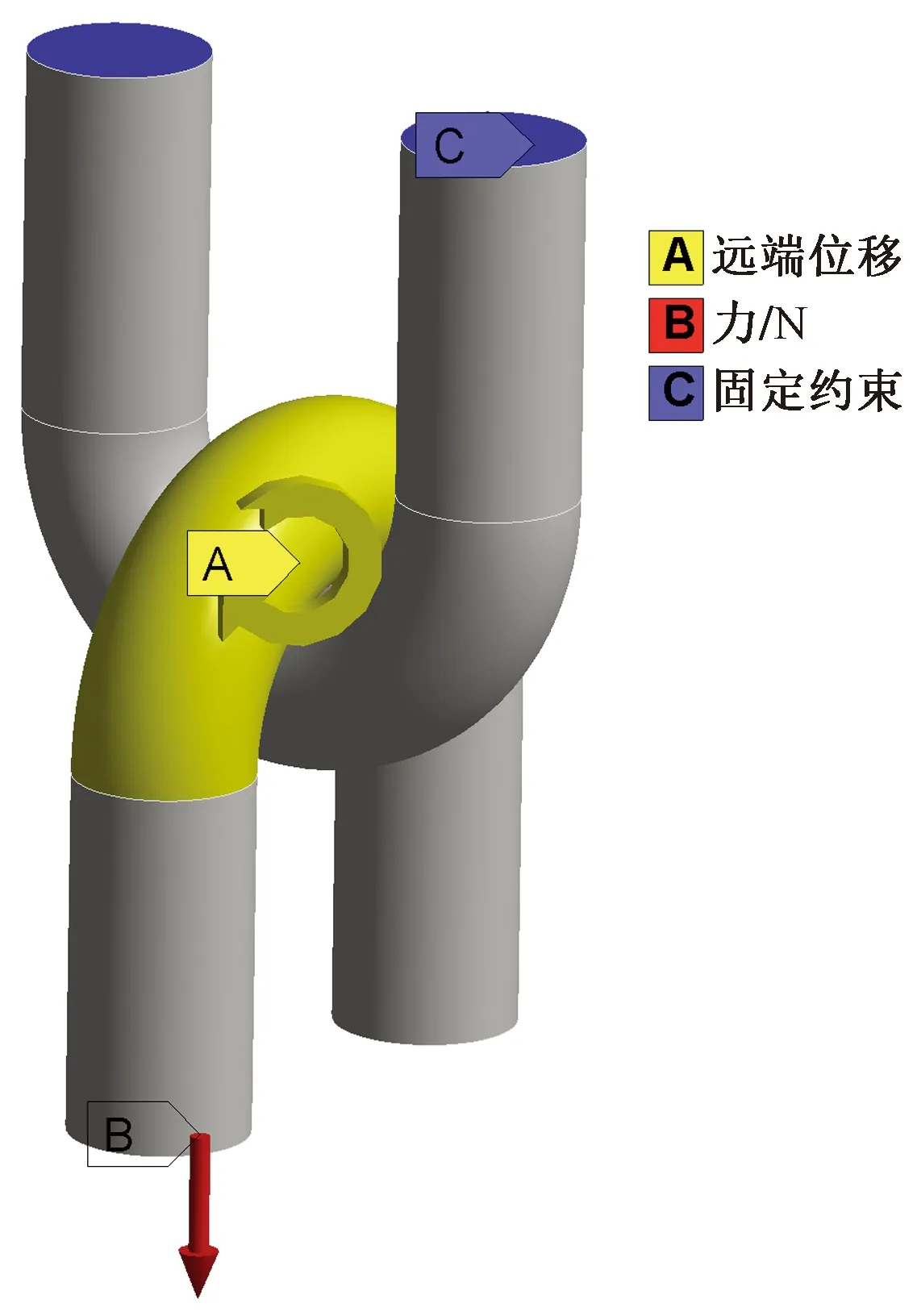
圖9 U形環有限元模型

網格劃分是有限元分析至關重要的一步,網格質量好壞直接決定了后續數值計算分析結果的準確性。以六面體單元為主要單元,對局部形狀復雜的部件采用四面體單元劃分,考慮結果精度的同時為了提高運算效率,對重點關注部件U形環接觸區域進行網格細化,非關注部件采用較為粗糙的網格,如圖10所示。針對導線不同覆冰狀態分別選取100 s內轉動角度和動張力變化劇烈區域進行計算,考慮到計算成本,計算時長為5 s。

3 整體連接金具應力場分析

在工程實際中,連接金具往往因導線振動引起的瞬時極大力出現變形和斷裂,連接金具整體結構復雜,各部件之間存在相互運動關系,因此進行動力學分析時收斂困難,因此,選取各類覆冰形式下的極大張力值作為輸入載荷進行靜力分析,具有一定的適用性。金具應力云圖如圖11所示,可以看出在最大張力的作用下,超出材料屈服極限的區域主要集中在U形環內側、聯板的側邊和內孔以及掛板的彎折處,最大應力值為509.0 MPa。

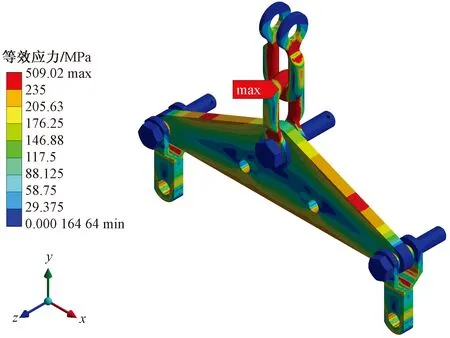
圖11 整體連接金具Von Mises等效應力云圖

從圖12可以看出,在U形環彎曲段外側,兩端的應力較小并向中間逐漸遞增,在頂部達到最大應力值為267 MPa,發生了塑性變形。U形環內側接觸部分的等效應力要略低于周邊,最大應力值出現在上下U形環接觸邊緣附近,結合圖13(a)中Y方向應力分量云圖可知該位置有較高的壓應力為977.2 MPa,此位置受Z向拉應力的作用發生變形,導致內部張力增大,結合圖13(b)中Z方向的應力分量云圖,該位置的拉應力達到了962.2 MPa。上下U形環接觸時相互擠壓,接觸面變形嚴重,由于彎曲段較窄,剪跨長度短,在接觸面邊緣出現應力集中現象,結合圖13(c)中YZ方向的剪應力分量云圖,該位置剪應力達到了178.4 MPa,此處也是拉斷試驗中最易斷裂部位。

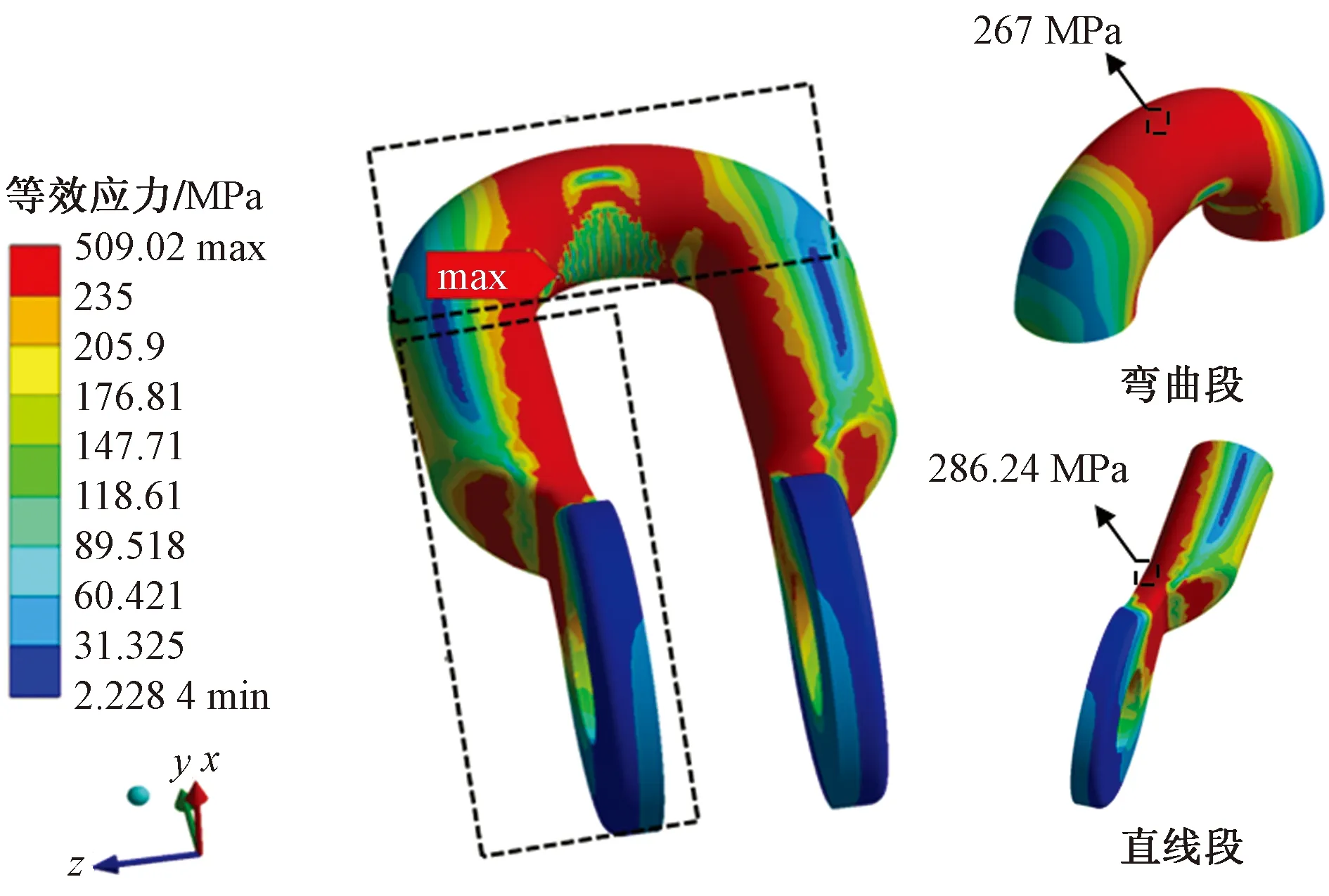
圖12 U形環Von Mises等效應力云圖

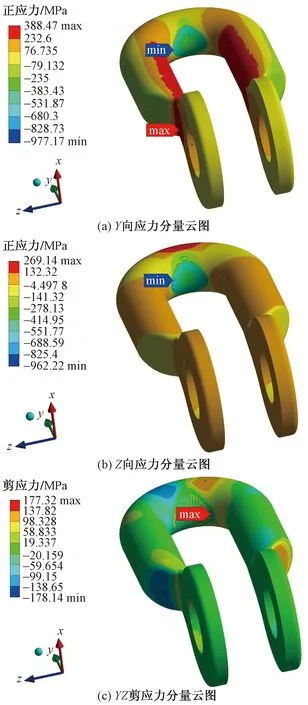
圖13 U形環應力分量云圖

在U形環直臂段中,內側等效應力要高于外側區域,結合圖13(a)中Y方向的應力云圖可以看出,直臂段內側受拉外側受壓,在耳環與直臂段連接處拉應力最大為388.5 MPa,此處也是工程實際中較為薄弱的位置。

聯板上端被螺栓固定,下端由于受到對稱力的作用,從圖14可以發現,在側邊已經出現向外彎曲現象,導致中間等效應力大于兩側并向部件內部遞減,在下孔處應力達到最大值298.3 MPa。掛板上端通過螺栓和聯板綁定,下端受到豎直向下的力,從圖15可以發現,在掛板彎折處以及內孔處出現了應力集中現象,最大應力值為286.2 MPa,在結構薄弱處極易發生斷裂失效。

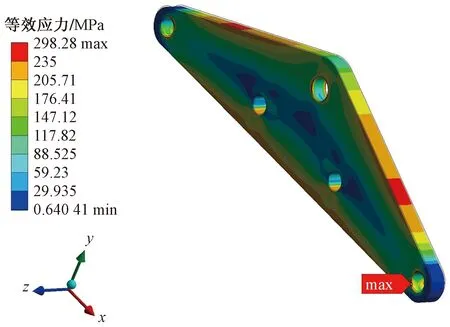
圖14 聯板Von Mises等效應力云圖

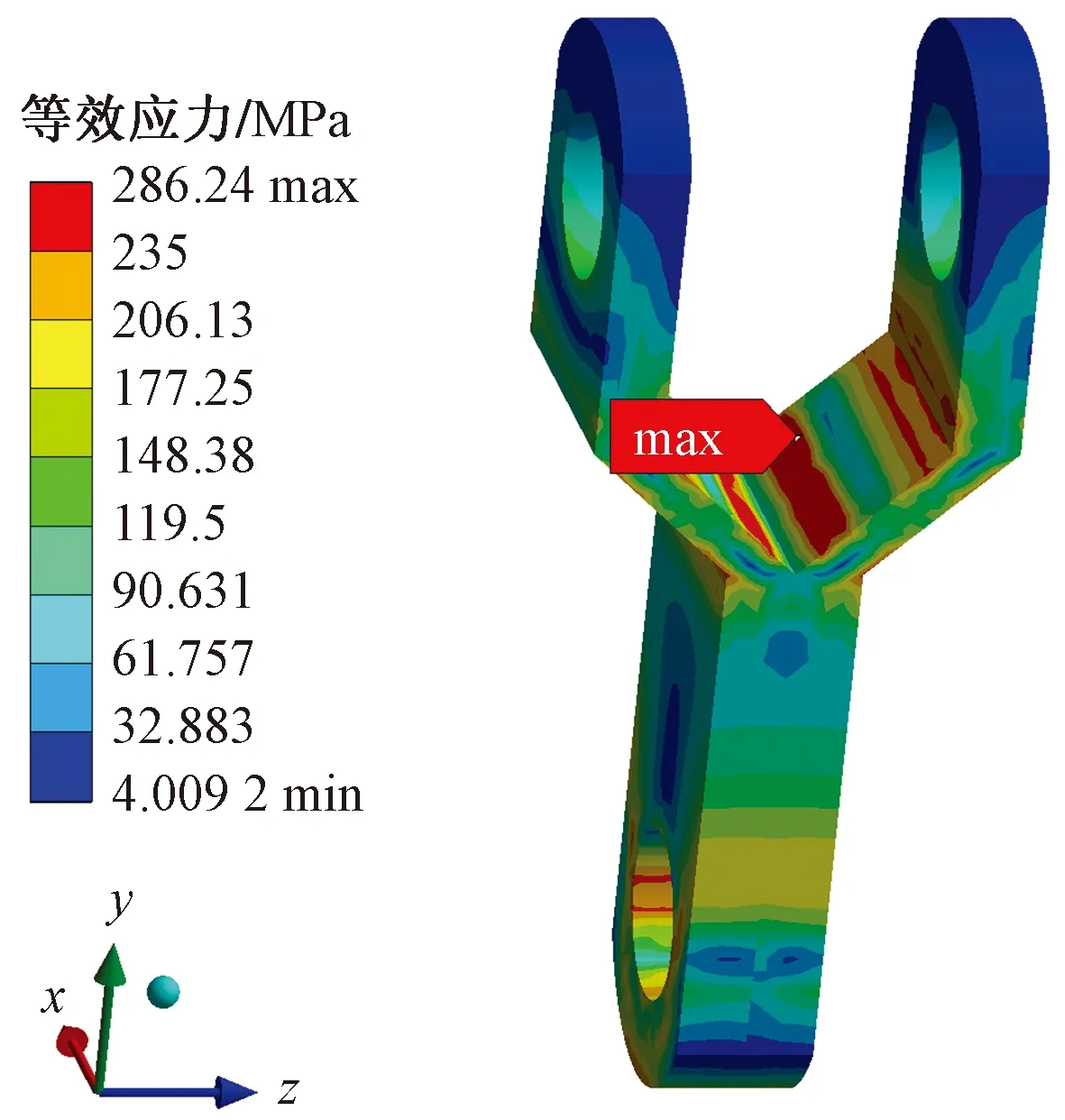
圖15 掛板Von Mises等效應力云圖

通過分析發現,在連接金具整體結構中,U形掛環最容易出現失效,其次是聯板孔洞處與掛板彎折處。

4 U形環應力場分析

4.1 覆冰形式影響分析

針對連接金具中的危險部件U形掛環進行瞬態動力學分析,計算時長為5 s。圖16為不同覆冰形式下U形環最大等效應力分布情況,從圖中可知,在風荷載作用下U形環發生轉動,應力集中區域在U形環底部分布具有不確定性,這和風場的隨機特性導致的轉動差異有關。從圖中還可以看出,覆冰形式對最大應力值與塑性變形范圍也有影響,均勻覆冰時,隨著覆冰厚度的增大加劇了U形環應力極大值,當覆冰厚度達到15 mm時,最大應力值達到996.4 MPa,相比于未覆冰最大應力值增大39.08%,且隨著覆冰厚度的增大,U形環等效應力超出材料屈服極限的面積擴大,在覆冰15 mm時,U形環大部分區域都發生了塑性變形;不均勻覆冰時,中央重覆冰最大應力值與兩側重覆冰相近,但發生塑性變形的區域面積明顯大于兩側重覆冰。

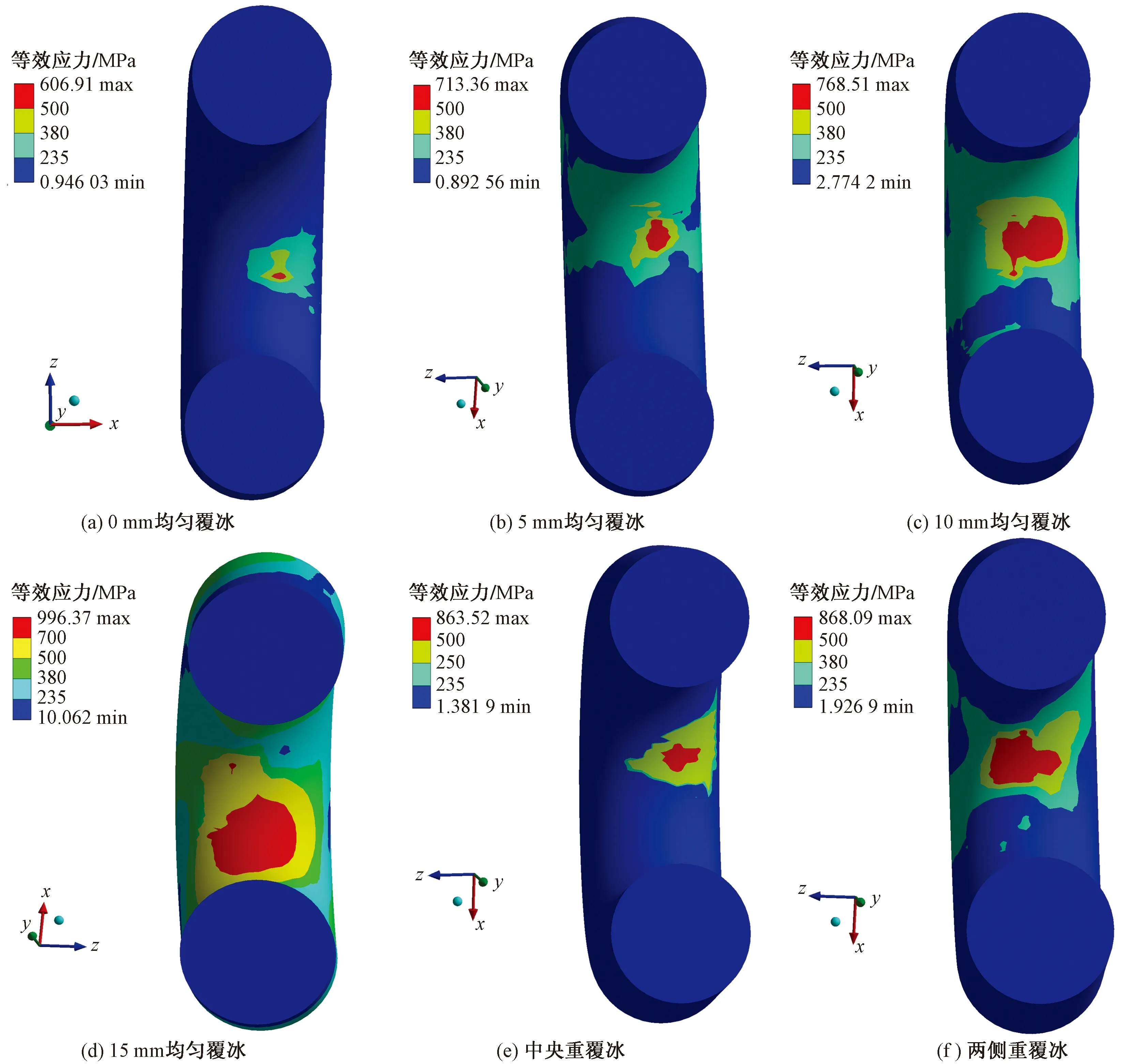
圖16 不同覆冰形式下U形環應力分布

通過分析發現,在隨機風作用下,U形環應力分布具有不確定性,可能會出現單側應力集中現象,因此只是單純的對U形環做單一方向拉斷與磨損試驗具有一定的局限性,并且要考慮在均勻覆冰時最大覆冰厚度對金具的影響,不均勻覆冰時,要對中央重覆冰進行重點關注。

4.2 受力形式影響分析

針對不同覆冰形式輸電導線,探究U形環之間有無轉動關系對最大應力值的影響,提取5 s內U形環受動張力無轉動關系以及受動張力有轉動關系的最大應值變化曲線,結果如圖17所示。可以發現,在張力值變化初期,有轉角和無轉角作用下的最大應力值均出現了劇烈的波動,這和材料本身性質有關,在張力增大時,U形環處于彈性變形階段應力、應變呈比例變化,因此最大應力值呈線性增長;當施加的外力繼續增大,材料達到屈服階段,應力不變,應變不斷增加導致接觸面積增大,使得最大應力值出現下降趨勢,由于時間間隔較短,轉動關系不明顯,動張力占主導地位,因此有轉角和無轉角狀態下U形環最大應力值變化趨勢基本一致。隨著張力的繼續增大,最大應力值變化趨勢放緩,此時由于轉角的持續增大,轉動關系明顯,兩種狀態下的最大應力值出現明顯的差異,可以發現,有轉角狀態下的U形環最大應力值要大于無轉角狀態,分析原因是因為U形環接觸面積隨著轉動而減小,增大了接觸壓力。

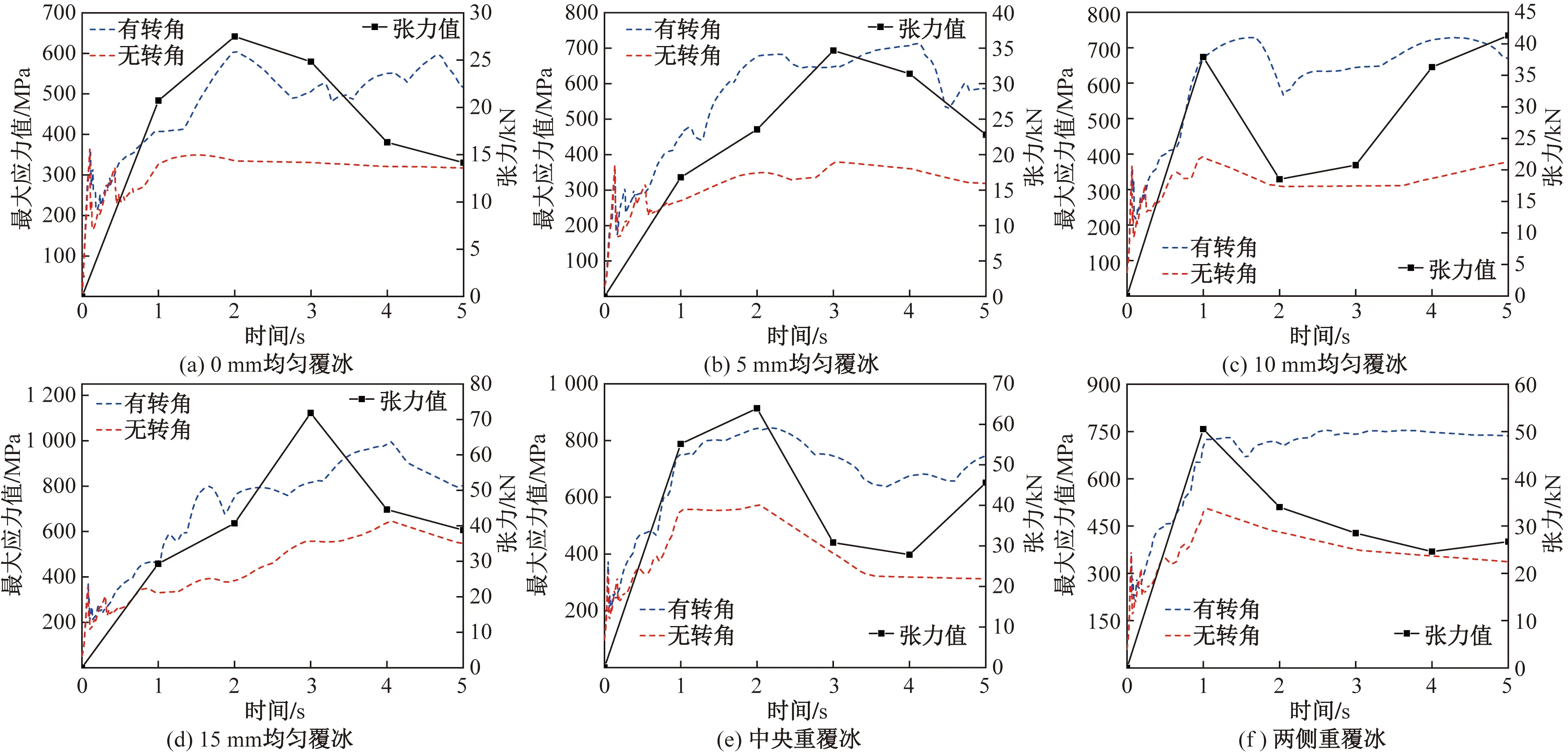
圖17 不同覆冰形式下U形環最大應力變化曲線

分別提取5 s內兩種狀態下U形環最大應力值的極大值,如圖18所示。可以發現,均勻覆冰時,應力極大值隨著覆冰厚度的增大而增大,在覆冰 15 mm 時達到最大,純張力作用時,極大值為 646.1 MPa,純在轉動關系時的極大值為 996.4 MPa,比純張力作用時增大35.15%。不均勻覆冰時,兩種狀態下中央重覆冰的極大值均大于兩側重覆冰,極大值分別為868.1、573.0 MPa和863.5、506.4 MPa。

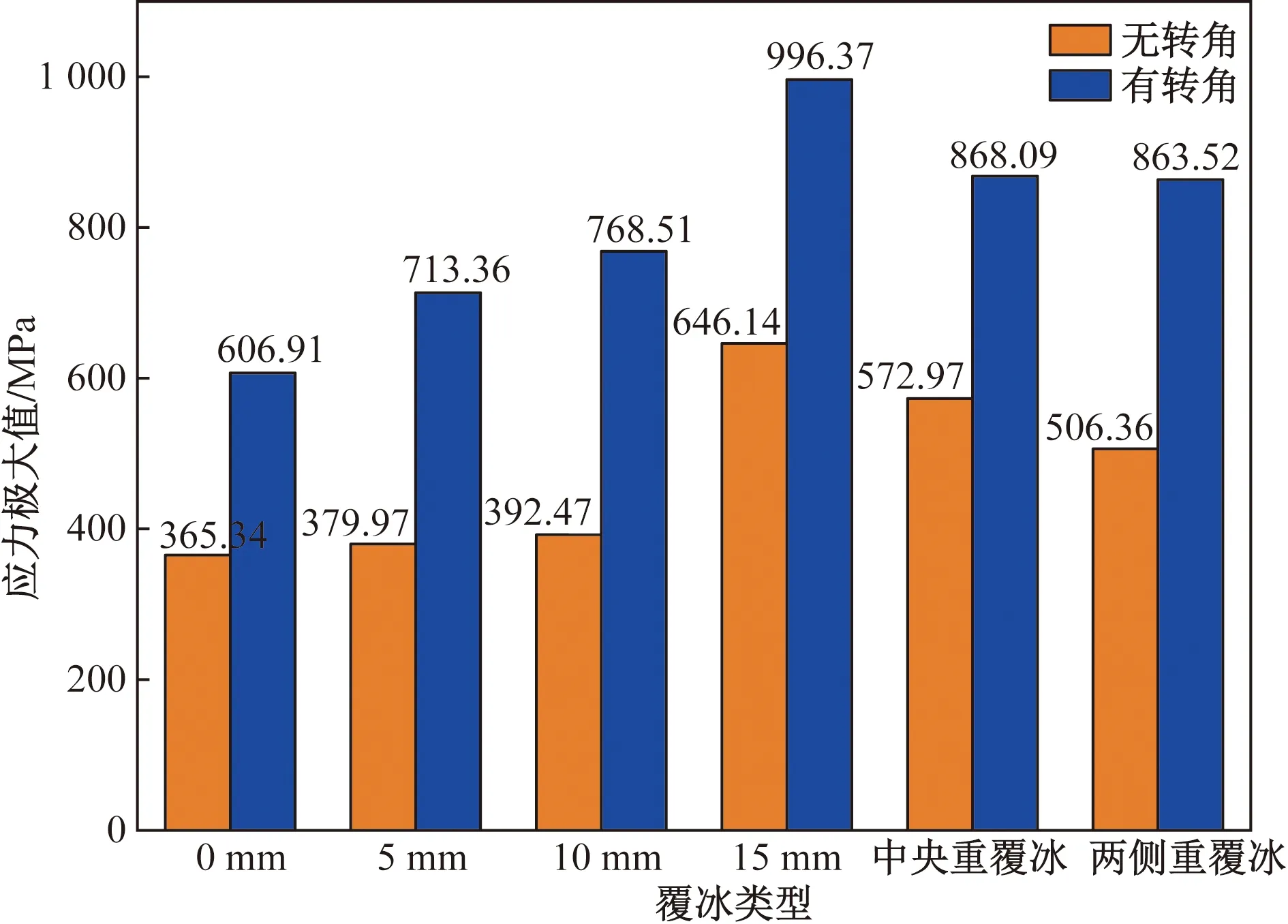
圖18 不同覆冰形式下U形環應力極大值

通過分析發現,當U形環間存在轉動時要比純張力作用下對U形環損害更加嚴重;均勻覆冰時,在覆冰厚度為15 mm時,U形環最大應力極大值達到最大;不均勻覆冰時,中央重覆冰U形環最大應力極大值要大于兩側重覆冰。可以看出,冰風荷載均對連接金具應力大小產生了顯著的影響,有必要針對冰封耦合環境下連接金具的安全性做深入研究。

5 結論

通過數值模擬獲得不同覆冰形式下輸電線路關鍵點處動張力和位移;研究了整體連接金具中應力分布狀況,并對危險金具U形環進行瞬態響應分析,得到覆冰形式、張力變化、受力形式對U形環最大應力值的影響,得出以下結論。

(1)最大覆冰張力下,整體連接金具中U形掛環連接處應力最大為509.0 MPa,發生塑性變形,其次是聯板孔洞處與掛板彎折處。

(2)均勻覆冰時,U形環最大應力值隨著覆冰厚度的增大而增大;線性覆冰時,中央重覆冰要比兩側重覆冰受力變形區域更大,危險性更高。

(3)在動張力作用下,當U形環間存在轉動關系時要比純張力作用下對U形環損害更加嚴重。