壓電驅動的橋式放大機構設計與優化

伍建軍,周敏,章仕磊

(1.天府新能源研究院,成都 610000; 2.江西理工大學機電工程學院,贛州 341000)

柔順機構利用柔性鉸鏈代替裝配復雜的運動關節,不僅無摩擦、靈敏度高,且一次加工成型,特別適用于精密微動領域。但柔性鉸鏈通過形變產生運動,運動范圍受限,需要位移放大機構實現相關功能[1-2]。

目前研究的放大機構有多級杠桿放大機構、差動杠桿放大機構、三角放大機構和橋式放大機構等,它們都具有各自的特點,如Li等[3]和Iqbal等[4]設計的多級杠桿放大機構雖然原理簡單,在一定條件下也能實現較大的放大倍數和負載能力,但是往往需要多級杠桿才能達到需要的放大倍數,這也造成了誤差累積和整體結構笨重。Fan等[5]設計的差動式杠桿放大機構雖然具有6.5倍的放大倍數和較高的固有頻率,但是體積大而且分析較為復雜。Lu等[6]設計的非對稱三角放大機構也存在著體積大,放大倍數不足等缺點。反觀Huang等[7]和Wu等[8]設計的橋式放大機構不僅結構緊湊,且機構所得到的放大倍數和固有頻率都較大。在力學研究方面,郝云鋒等[9]設計了多級的嵌套菱形結構,并對其進行了分析與計算。閆洪波等[10]采用計算鉸鏈中心點偏移量的方法來近似得出輸入輸出位移以計算放大倍率。林超等[11]通過能量守恒方法和彈性梁理論推導出了放大比公式和剛度計算解析式,并根據拉格朗日方程得出固有頻率計算方法。Ling等[12]綜合橋式和杠桿式柔順機構,提出一種結構緊湊的新型混合三級兼容位移放大器,不僅在放大效率上有所提升,而且結構尺寸僅為57 mm×50 mm×10 mm。Chen等[13]基于偽剛體法計算輸入變量與輸出變量的關系,通過仿真分析驗證了理論計算的正確性。

但是,傳統許多針對橋式放大機構的力學研究中,沒有明確菱形結構與橋式結構的區別,簡單地把橋式結構簡化成用連桿代替的菱形結構進行力學分析,這種不適當的簡化可能導致柔順機構的理論預測不準確。

為了說明和澄清菱形機構和橋式機構之間靜態建模的混淆。現給出位移放大比的精確解析,以提高柔順機構的輸出位移的預測精度。然后,對橋式放大機構進行強度分析和動態特性分析,并通過ANSYS仿真驗證理論模型的正確性。最后基于最優拉丁超立方試驗設計方法獲取數據,通過徑向基函數(radial basis function,RBF)神經網絡和多島遺傳算法(multi-island genetic algorithm,MIGA)對橋式放大機構進行多目標優化。預想通過靜力學分析對橋式放大機構的放大倍數有更加精確預測,通過參數優化能進一步提高橋式放大機構的放大倍率和固有頻率,擴大橋式放大機構的使用范圍和響應速度。

1 結構模型

圖1所示為橋式放大機構,該機構的結構對稱,由8個柔性鉸鏈、4個連梁、2個平移桿,1個輸出塊和1個固定塊組成[14]。在兩個輸入端各產生Δx的輸入位移,相應的在輸出塊位置產生2Δy的輸出位移。

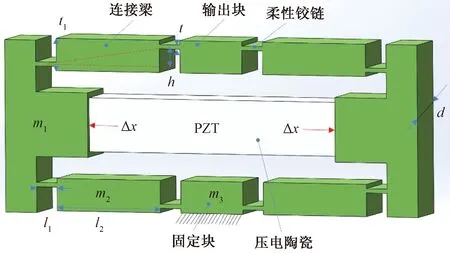
t為柔性鉸鏈的厚度;t1為連接梁的厚度;d為橋式放大機構的寬度;l1和l2分別為柔性鉸鏈和連接梁的長度;h為兩個柔性鉸鏈的間距;m1、m2、m3為連接梁的質量;PZT為壓電陶瓷;Δx為壓電陶瓷的驅動位移

2 靜力學分析

2.1 位移放大比分析

2.1.1 歐拉-伯努利梁模型

根據如圖1所示的橋式放大機構取如圖2所示的一部分結構進行靜力學分析,連接梁及柔性鉸鏈的受力方程為

圖2 部分結構受力圖

fA=fB=fx=fPZT

(1)

2Mr=fxh

(2)

式中:fA和fB為連接梁所受的水平力;fx為柔性鉸鏈受的拉力;Mr為柔性鉸鏈受的力矩;fPZT為壓電陶瓷產生的輸入力。

根據能量守恒原理,力fPZT所做的功轉化為柔性鉸鏈的彎曲勢能和拉伸變形能。

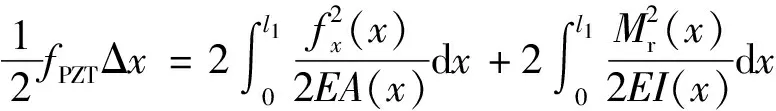
(3)

式(3)中:Δx為輸入位移;Mr(x)為柔性鉸鏈受的力矩;fx(x)為柔性鉸鏈受的軸向力;A(x)和I(x)為柔性鉸鏈橫截面積和慣性矩;E為楊氏模量。

根據胡克定律,可以得到

fx=Kl1Δl1

(4)

式(4)中:fx為柔性鉸鏈所受的軸向拉力;Kl1、Δl1分別為柔性鉸鏈的拉伸剛度和軸向伸長量。

將式(4)代入式(3)并求解積分得到橋式放大機構的軸向位移為

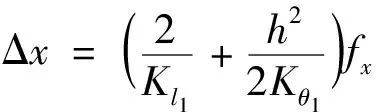
(5)

式(5)中:Kθ1為柔性鉸鏈的轉動剛度。

使用歐拉-伯努利梁理論計算變形梁的擾度作為輸出位移Δy,即

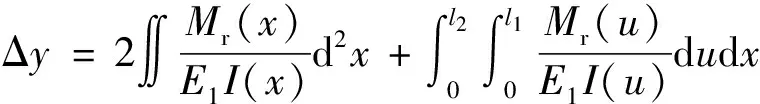
(6)

式(6)中:E1為修正后的楊氏模量。

對式(6)求解積分得到輸出位移為

(7)

式(7)中:l1、l2分別為柔性鉸鏈、連接梁的長度。

因此,聯立式(5)和式(7)得到歐拉-伯努利梁模型的放大比為

(8)

2.1.2 考慮連接梁變形的歐拉-伯努利梁模型

考慮連接梁的變形,則輸入力fPZT所做的功轉化為柔性鉸鏈和連接梁的彎曲勢能與拉伸變形能,得到橋式放大機構的輸入位移為

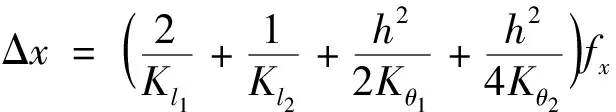
(9)

式(9)中:Kθ2和Kl2為連接梁的轉動剛度和拉伸剛度。

由剛度矩陣可知Kl1、Kθ1、Kθ2和Kl2的值分別為[15]

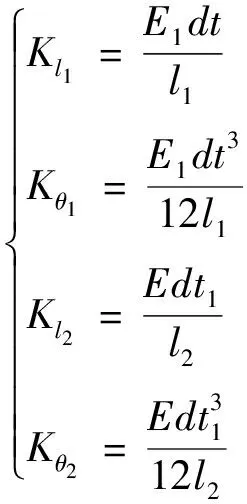
(10)

式(10)中:d為柔性鉸鏈的寬度;t為柔性鉸鏈的厚度。

當d>10t時,楊氏模量E應修正為E1[15],即

(11)

式(11)中:v為泊松比。

柔性鉸鏈和連接梁的擾度之和作為橋式放大機構的輸出位移Δy為

(12)

對式(12)求解積分得到輸出位移為

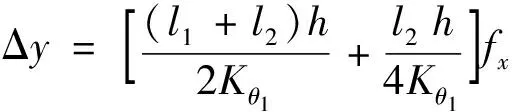
(13)

因此,聯立式(5)和式(13)得到考慮連接梁變形的歐拉-伯努利梁模型的放大比為

(14)

2.1.3 二自由度模型

Δy為輸出位移;fN為連接梁所受的拉力;α為變形前桿AB與水平線的夾角;α′為變形后桿AB與水平線的夾角;Δα=α-α′圖3 橋式機構簡化原理圖

將橋式放大機構簡化為如圖3所示的類似菱形的連桿結構[16],機構在輸入力的作用下從實線位置變為虛線位置,橋式放大機構變形前連接梁兩端的柔性鉸鏈回轉中心是點A和點B,變形后連接梁兩端的柔性鉸鏈回轉中心變成了點A′和點B′,桿AB的水平夾角α在輸入力作用下變為α′。

由式(1)可知fA=fB=fx,根據圖3在連桿端點A處建立力矩和力方程為

fxh=2Mr=2Kθ1Δα

(15)

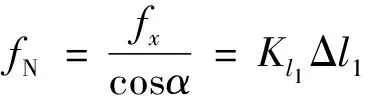
(16)

根據虛工原理,建立能量方程

fxΔx=fNΔl1+2MrΔα

(17)

聯立式(15)～式(17)可得橋式放大機構的軸向位移Δx為

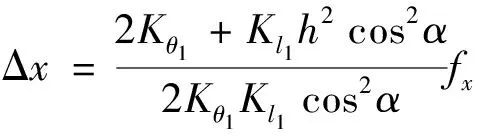
(18)

根據圖3可得

ly=lABsinα

(19)

式(19)中:lAB為點A和B之間的長度。

對式(19)兩邊求全微分得到

dly=lABcosαdα+sinαdlAB

(20)

用微小增量代替微分得

Δy=lABcosαΔα+sinαΔlAB

(21)

由式(15)和式(16)得到Δα和Δl1,并代入式(21)得

(22)

因此,聯立式(18)和式(22)得到二自由度模型的放大比為

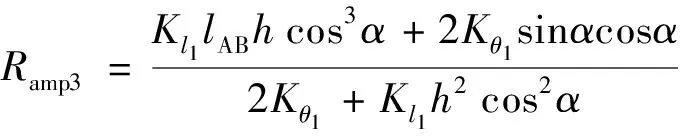
(23)

將3種放大比模型以及單自由度模型[17]的計算結果與軟件Workbench17.0的仿真結果做比較。從圖4可以看出考慮連接梁變形的歐拉-伯努利梁模型的輸出位移值與仿真值最接近,說明考慮連接梁變形的歐拉-伯努利梁模型具有更高的預測精度。

圖4 各模型的放大比

2.2 應力分析

要保證材料在彈性變形范圍內產生形變,需要滿足最大應力小于許用應力,應力為

(24)

式(24)中:W為柔性鉸鏈的抗彎截面系數;A為柔性鉸鏈的截面面積。

3 動態特性分析

對橋式放大機構進行動態特性分析,因其只有y方向上一個自由度的輸出,取輸入位移為廣義坐標q,根據圖1機構模型,橋式放大機構系統動能可以表示為

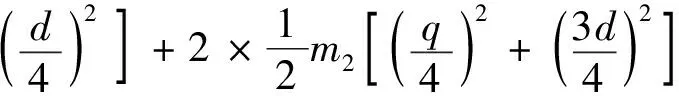
(25)

式(25)中:q為輸入位移;d為輸出位移,根據式(23)求出d=Ramp2q。

根據拉格朗日方程[18],橋式放大機構的等效質量M和等效剛度K分別為

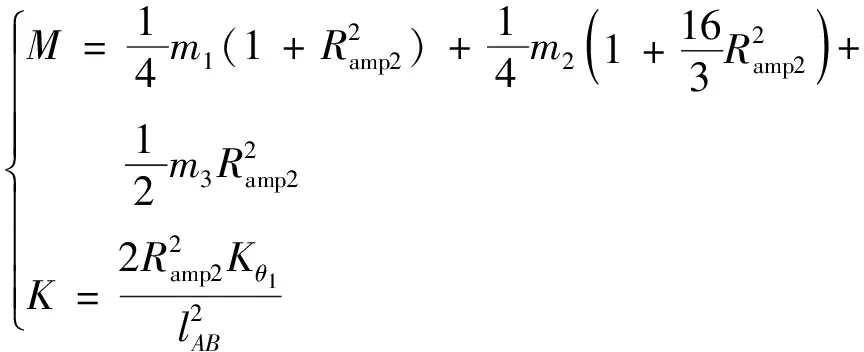
(26)

橋式放大機構固有頻率為

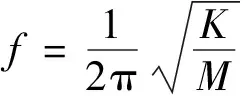
(27)

4 理論模型驗證

為驗證理論模型,采用ANSYS對放大機構進行有限元仿真,機構尺寸如表1所示,材料選用AL-7075鋁合金,其彈性模量為71.7 GPa,泊松比為0.33,密度為2 810 kg/m3,屈服強度為503 MPa。根據放大機構的尺寸選擇網格密度為0.5 mm。

將固定塊固定,在x軸兩端各輸入10 μm的位移,得到橋式放大機構的輸出位移、固有頻率和應力,應力分布如圖5所示,將仿真值與理論值對比,對比結果如表2所示。

表2 仿真值與理論值比較分析

圖5 應力分布圖

根據圖5的應力分布圖可知,最大應力產生在柔性鉸鏈中間處,最大應力為40.58 MPa,遠小于屈服極限,強度符合要求。從表2對比結果可以看出各性能的理論值誤差均在7%以內,證明了理論模型的正確性。

5 參數優化

5.1 RBF神經網絡模型的建立

由于橋式放大機構的響應與參數的關系難以用顯式函數擬合,RBF神經網絡模型屬于非線性模型,能夠通過有限的樣本點建立響應與參數之間的關系模型,利用該模型預測非樣本點的響應值,為橋式放大機構的結構參數設計提供優化模型。以橋式放大機構的放大倍數和固有頻率作為性能指標,柔性鉸鏈的長度l1和厚度t,連接梁的長度l2和厚度t1以及兩個鉸鏈的間距h尺寸作為參數,各參數的取值范圍如表3所示,根據表3的取值范圍使用最優拉丁超立方抽樣確定試驗點并計算對應的響應值,結果如表4所示。

表3 參數取值范圍

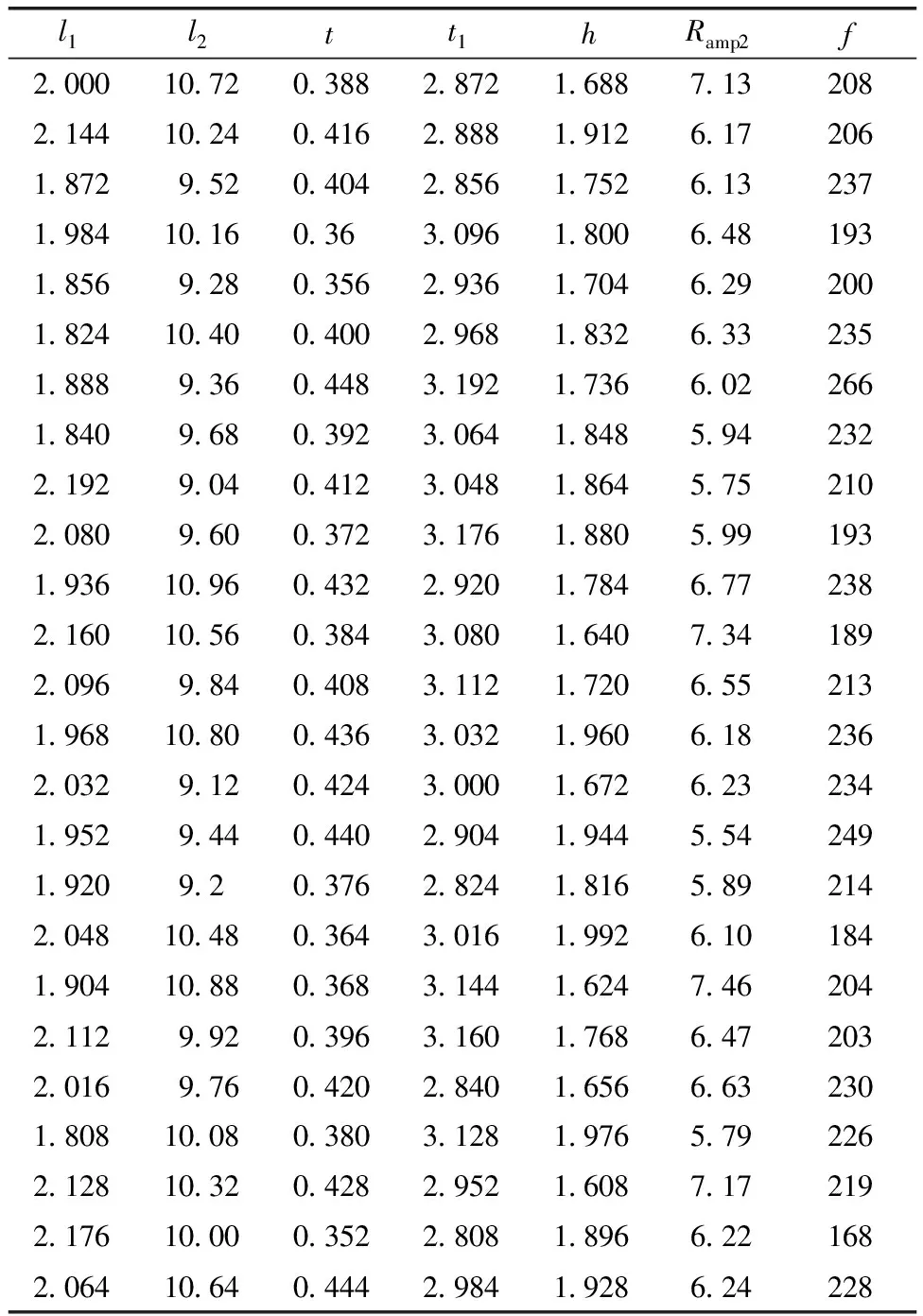
表4 試驗設計數據表

(RBF)神經網絡是具有3層結構的網絡類型,分別為輸入層、隱含層和輸出層。輸入層接收輸入信號并傳遞到隱含層,輸入層節點個數取決于輸入變量個數,隱含層也稱中間層,該層中的隱元素使用非線性變換函數將輸入映射至新的空間。輸出層常用線性函數作為傳遞函數,輸出層節點個數取決于響應個數。根據本文5個參數兩個響應,構建RBF神經網絡模型如圖6所示。

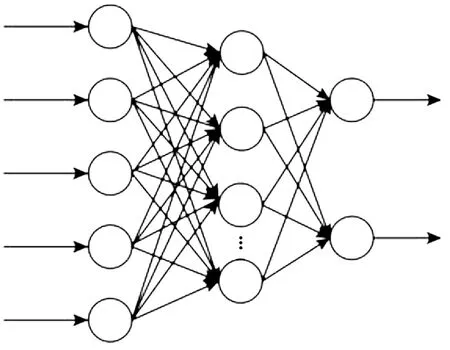
圖6 RBF神經網絡模型

對于RBF神經網絡,使用高斯函數[19]作為徑向基函數,函數形式為

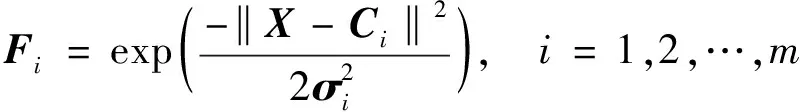
(28)

式(28)中:Fi為隱含層的輸出;X為n維輸入向量;Ci為權值向量,與X具有相同的維數;σi為第i個隱含層節點變量,其確定了基函數半徑;‖X-Ci‖為向量X-Ci的歐幾里德范數;m為隱含層的節點個數。

5.2 RBF神經網絡模型擬合精度檢驗

將表4中的數據當作訓練樣本,應用MATLAB自帶工具箱中的newrb函數建立RBF神經網絡模型。采用最優拉丁超立方抽樣設計10組檢驗樣本點,通過ANSYS仿真獲得橋式放大機構這10組檢驗樣本的放大倍數和固有頻率值列于表5,通過這10組檢驗樣本點驗證模型的擬合精度。

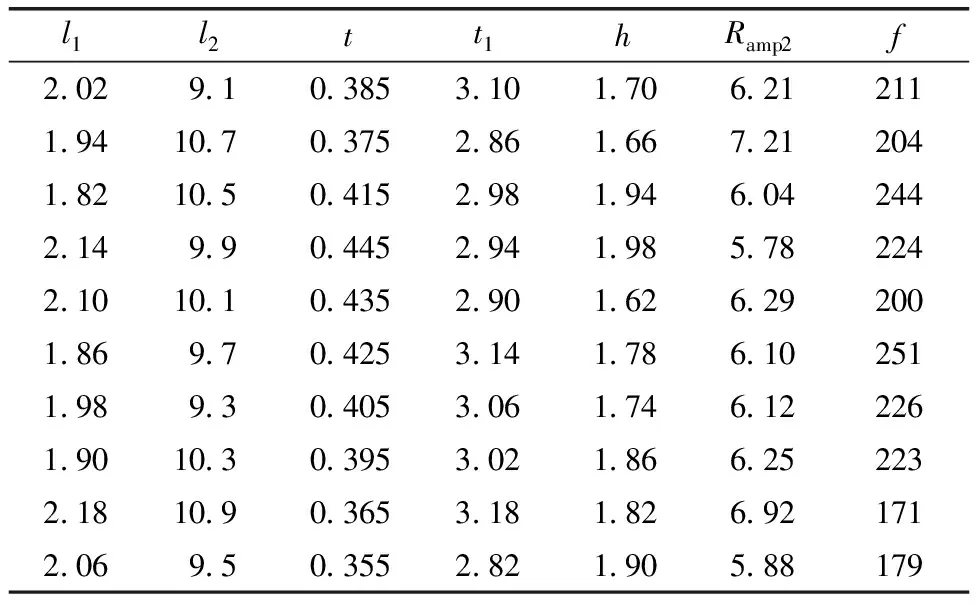
表5 檢驗樣本

調用MATLAB中的sim函數,輸入變量是表5中的10組數據,得到RBF神經網絡模型對放大倍數和固有頻率的預測,預測值分別用R′amp2和f′表示,如表6所示。

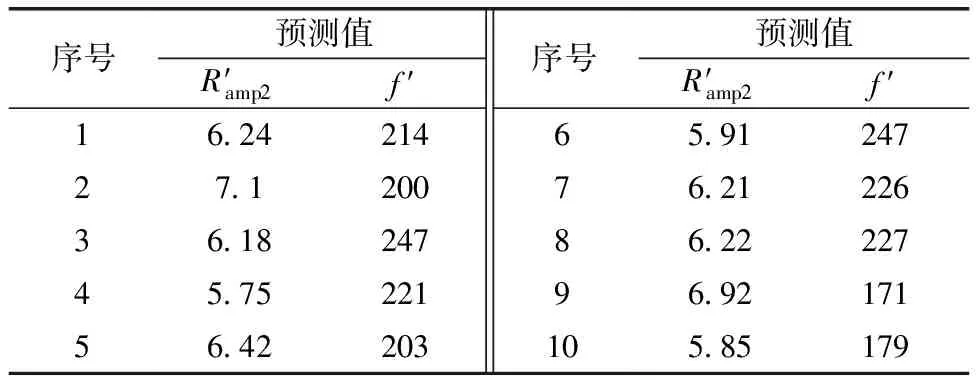
表6 RBF神經網絡模型預測結果

可決系數可以用來評價RBF神經網絡模型的擬合精度,其計算公式[20]為

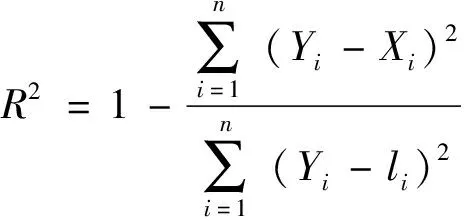
(29)

式(29)中:R2為可決系數;Xi為預測值;Yi為模擬值;n為試驗次數;li為模擬值的平均值。

將表5檢驗樣本中的響應值與表6中的響應預測值代入式(29),分別計算得到放大倍數RBF神經網絡模型的可決系數R2=0.948 1和固有頻率RBF神經網絡模型的可決系數R2=0.941 2,R2均接近1,說明RBF神經網絡模型的擬合精度較高。圖7放大倍數與圖8固有頻率的仿真值和RBF神經網絡的預測值非常接近,直觀地證明了RBF神經網絡模型的擬合精度較高。

圖7 放大倍數模擬值與預測值對比圖

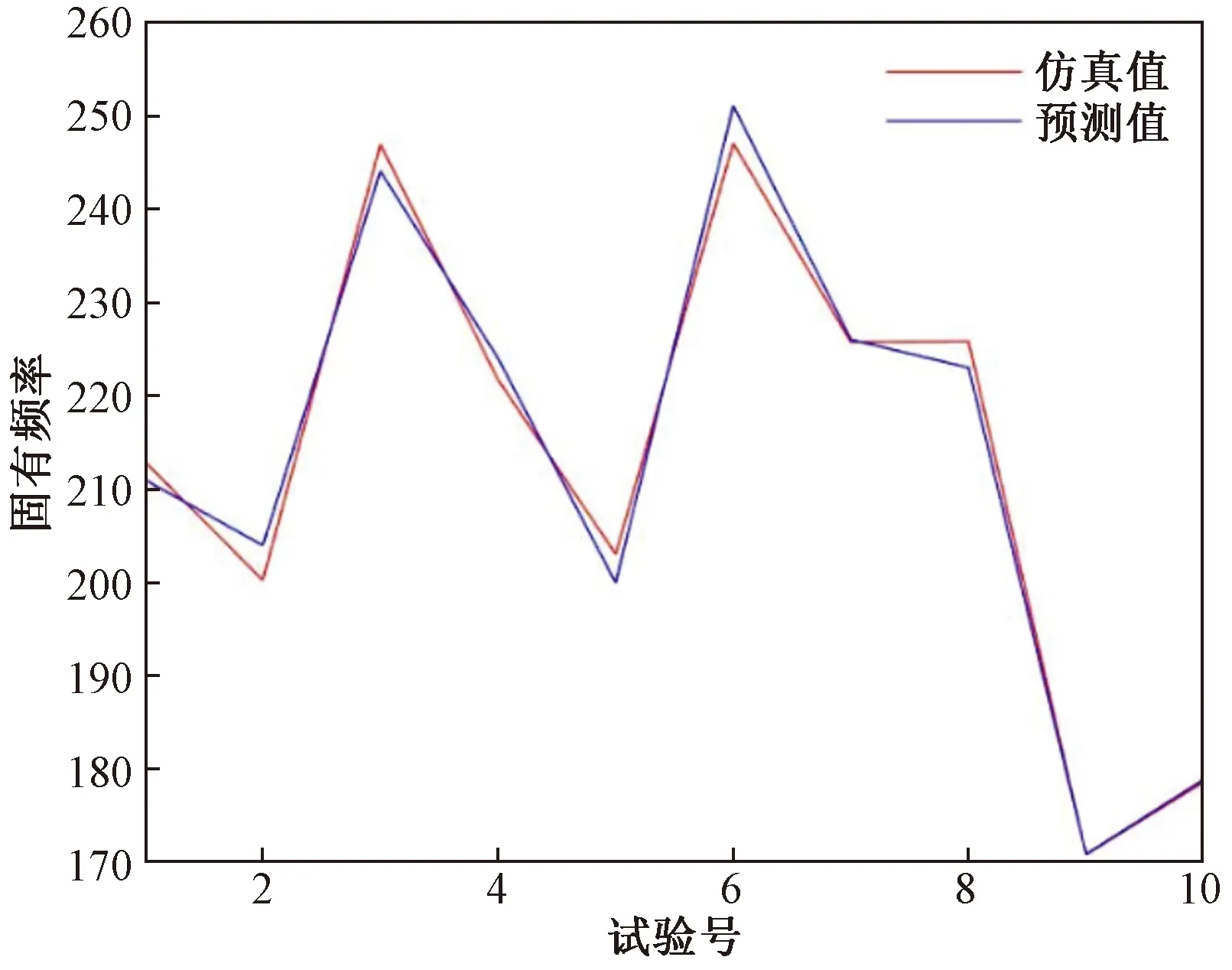
圖8 固有頻率模擬值與預測值對比圖

5.3 基于多島遺傳算法(MIGA)的多目標優化

MIGA將種群分成多個島嶼共同并行進化,相比于其他算法,它適用于參數較多的尋優。具有全局性,能避免陷入局部最優,而且求解速度快。在建立的RBF神經網絡模型內進行全局尋優,各結構參數的取值范圍如表3所示,MIGA的參數值設置如表7所示。尋優得到的參數值如表8所示。

表7 MIGA參數

表8 優化結構參數

將參數優化前與參數優化后的性能指標進行對比分析,對比結果如表9所示。由表9可知優化后的放大倍數7.34,相比優化前的6.33倍提高了16.0%,優化后的固有頻率237 Hz,相比優化前的198 Hz提高了19.7%,優化結果符合預期,證明建立的RBF神經網絡模型和采用的MIGA是準確可靠的。

表9 橋式放大機構優化前與優化后性能指標

6 結論

(1)通過對比分析可知,將變形梁的擾度作為輸出位移,考慮連接梁變形的歐拉-伯努利梁模型對放大比的預測精度最高,通過仿真分析驗證,放大倍數、固有頻率和最大應力的理論值與仿真值的誤差均在7%以內,驗證了理論模型的正確性。

(2)使用最優拉丁超立方抽樣確定試驗點,用ANSYS仿真獲得試驗點的放大倍數和固有頻率,采用RBF神經網絡理論建立關鍵參數與響應之間的非線性模型,為橋式放大機構的尋優提供近似模型,最后通過多島遺傳算法尋優,結果表明放大倍數提高了16.0%,固有頻率提高了19.7%,證明了所采用的優化方法具有明顯效果。