基于改進粒子群算法的城市物流無人機路徑規劃

王飛,楊清平

(中國民航大學空中交通管理學院,天津 300300)

隨著中國電子商務迅猛發展,物流業爆發式增長。隨著國家低空空域改革持續進行,以及無人機自動化技術、移動通信技術的發展,無人機為解決城市物流“末端一公里”帶來新的途徑[1]。作為無人機任務規劃系統的核心之一,無人機路徑規劃是根據安全、高效等目標優化設計飛行路徑。無人機路徑規劃分為靜態路徑規劃和動態路徑規劃,靜態路徑規劃主要應用于無人機路徑預規劃,而動態路徑規劃主要應用于無人機任務期間針對避障、任務變化等原因造成的實時路徑重規劃。本文研究聚焦無人機任務預規劃階段的靜態路徑規劃。

根據應用環境和智能化程度不同,無人機靜態路徑規劃算法包括基于圖搜索算法、基于采樣搜索算法和基于進化的算法[2]。基于圖搜索算法包括了A*和D*等;基于采樣的搜索算法包括了隨機路標圖法、快速擴展隨機樹法等;基于進化的算法則包括粒子群算法(particle swarm optimization,PSO)、遺傳算法等。基于圖搜索算法被廣泛應用到無人機靜態三維路徑規劃問題,但難以在復雜城市環境下規劃出符合安全性的路徑。基于采樣的搜索算法不需要對環境進行建模,對于高維復雜環境有較好的適應性,但同時也有收斂速度慢、獲取初始可行路徑的時間較長等缺陷。基于進化的算法通過群體優化尋找規劃空間的最優解,具有隨機性、并行性的特點。

PSO算法是進化算法的典型代表,具有前期收斂速度快、魯棒性強、路徑平滑等優點,在無人機路徑規劃中得到廣泛應用,但PSO后期容易陷入局部最優解,導致收斂效率降低。針對物流無人機路徑規劃問題,中外學者對PSO進行了改進。孫雪瑩等[3]提出細菌覓食-遺傳-粒子群混合算法來解決PSO早熟的問題。趙紅超等[4]采用了量子粒子群優化算法,避免PSO陷入局部最優。Jamshidi等[5]利用并行粒子群優化算法,提高了計算效率。姚燦中[6]等提出變慣性權重及動態鄰域的方法,一定程度上避免陷入局部最優。

現基于無人機距離地面120 m以下的三維城市超低空環境并充分考慮了無人機飛行高度、最大俯仰角等性能限制,以配送運行總代價最小為目標構建無人機路徑規劃模型,設計混沌粒子群優化算法,以獲得最佳配送路徑。首先介紹城市空域環境建模,接著建立路徑規劃模型,然后設計改進的粒子群算法,最后進行仿真分析。

1 城市空域環境建模

環境建模,即將無人機飛行的實際物理空間抽象為便于數學描述和計算的環境模型。可視圖法、拓撲圖法和柵格法等在目前的環境建模中得到較多應用[7]。其中,柵格法憑借操作簡單易于構建在無人機路徑規劃應用中最為廣泛,即規劃空間劃分成若干個柵格單元,并賦予每個柵格單元相應的代價值,表示無人機經過該柵格單元所付出的代價。

在本文環境建模部分采用柵格法構建規劃空間為OABC-O′A′B′C′的立方體區域,其柵格像元粒度(邊長)為δg。設立長、寬、高分別為x、y、z,原點為O的三維直角坐標系,將規劃空間劃分為m×n×h個柵格,用每個柵格的中心點代表柵格,表征待選路徑點,其中m=int(x/δg),n=int(y/δg),h=int(z/δg),int為向下取整函數。

柵格像元粒度由空間分辨率和計算機性能決定。像元粒度過大導致規劃的路徑難以達到理論最優解,過小則導致計算機運行負荷大大增加,計算時間過長。柵格粒度也需要與無人機性能相匹配。城市低空環境中的靜態障礙物包括了構筑物和建筑物,將各個障礙物簡化為長方體,不考慮其鏤空結構,無人機通過繞飛或跨越方式進行避障。

傳統的0～1賦值法將存在障礙物的柵格賦值為1,不包含障礙物的柵格賦值為0。0～1賦值法優點在于構建簡單易于實現,缺點是精度不夠,忽視了可通過的柵格存在的潛在風險。為此,采用柵格危險度[8]的概念。如圖1所示,灰色的柵格存在障礙物,賦值為1,其余柵格危險度為其周圍26個柵格中含障礙物柵格所占比例。柵格i的危險度φi計算過程為

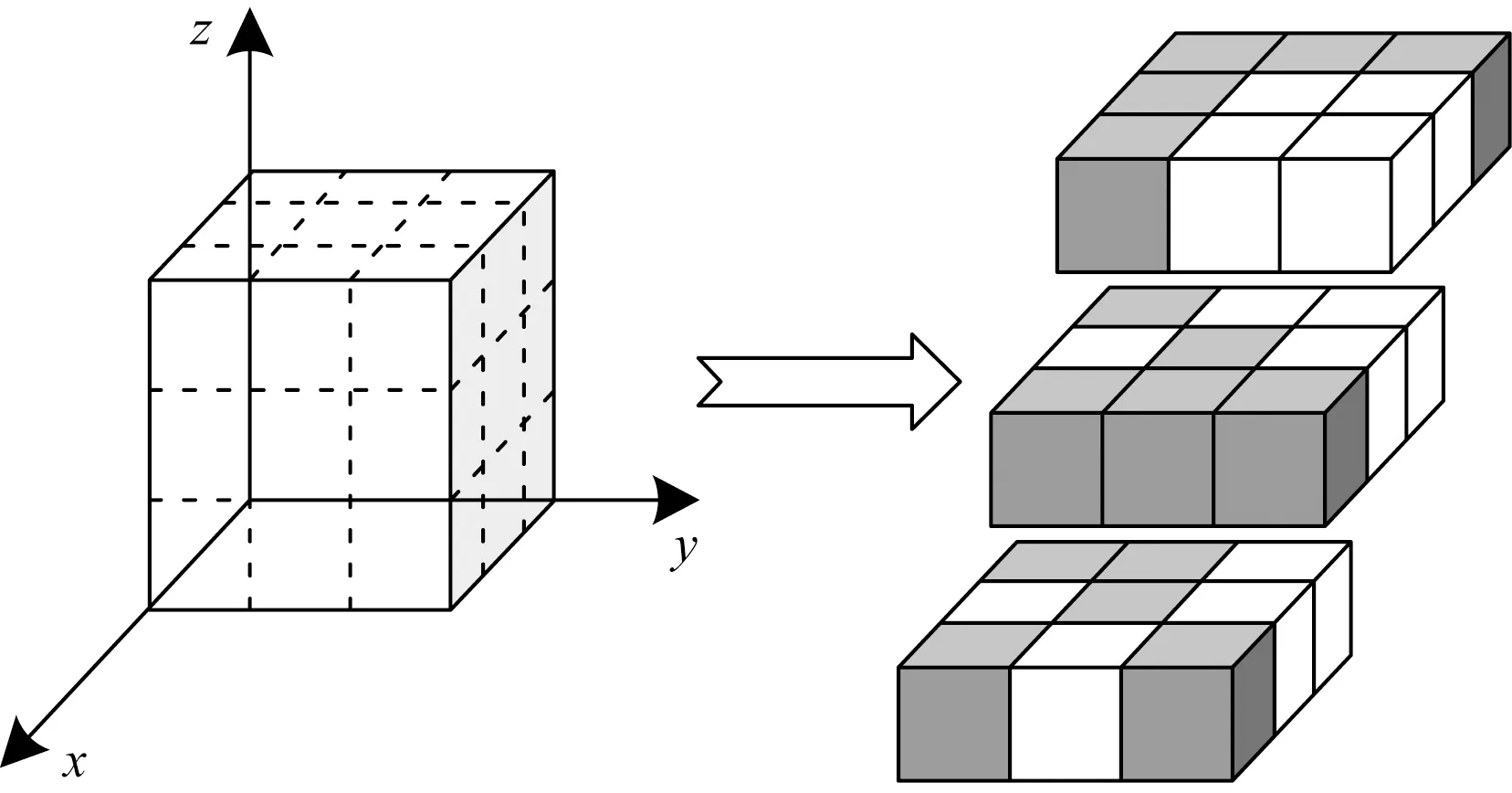
圖1 柵格危險度因子

(1)

式(1)中:Nobstacle(i)、Nsurrounding(i)分別為柵格i周圍含障礙柵格數和周圍柵格總數。

2 路徑規劃建模

假設某城市區域存在一個位置已知物流需求點,需派遣物流無人機向該點配送貨物,由可垂直起降的電動多旋翼無人機承擔配送任務。設起始S點坐標點為(x0,y0,z0),目標點G坐標(xn,yn,zn),中間路徑點為(xi,yi,zi),i∈{0,1,2,…,n}。在配送過程中,需要保障安全平穩飛行,以及降低能耗。與障礙物的位置關系直接影響飛行安全,飛行距離、頻繁的高度變化都會直接影響能耗及飛行平穩性。因此,本文研究基于飛行距離代價、飛行高度變化代價、危險度代價建立多目標函數。

2.1 目標函數

2.1.1 飛行距離代價

基于物流經濟性的考慮,飛行距離代價L越短則物流配送成本越低,由配送過程中間路徑節點間的歐氏距離之和表示,即

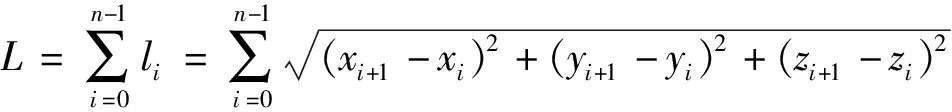
(2)

式(2)中:L為總配送路徑長度;li為每段路徑節點之間的歐式距離。

2.1.2 飛行高度變化代價

飛行過程中,頻繁發生高度變化會對無人機能耗造成不必要的消耗[9],飛行高度變化代價為

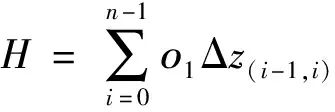
(3)

式(3)中:ο1為高度變化懲罰系數,無量綱;Δz(i-1,i)為第i個路徑點與第i-1個路徑點之間高度變化,m。

2.1.3 危險度代價

安全性用危險度代價表征。無人機從S到G的危險度代價為D,表示飛行路徑中各個柵格危險度φi之和,其中φi表示每個柵格周圍26個柵格中含障礙物柵格所占比例,使得路徑規劃中對無人機潛在的威脅得到考慮。計算過程為

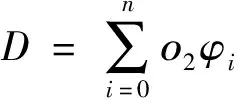
(4)

式(4)中:ο2為危險度懲罰系數,無量綱。

綜上所述,針對物流無人機配送路徑規劃問題,構建多目標函數,即

minJ=α1L+α2H+α3D

(5)

式(5)中:α1、α2、α3分別為飛行距離代價、飛行高度變化代價、危險度代價的權重系數,滿足α1+α2+α3=1。權重系數的設置根據場景需要確定。如果更加關注無人機的安全,則可以增加危險度代價的權重;如果更加關注任務完成的效率,則可以增加距離代價的權重;如果更加關注無人機能耗可以增加飛行高度變化代價的權重。

2.2 約束條件

(1)最小步長約束。受無人機姿態調整延遲的影響,為保證配送安全,無人機水平面以及垂直方向機動動作預留的直飛步長fi需要限制在定的最小步長fmin以內,公式為

fi≥fmin

(6)

(2)最大偏航角約束。最大偏航角是對無人機在水平面內的運動限制。考慮到機動性能限制,要求無人機需要在限定的偏航角范圍內完成機動轉彎。假設相鄰的兩個航路點的坐標分別為(xi,yi,zi)和(xi+1,yi+1,zi+1),且zi=zi+1,偏航角α計算過程為

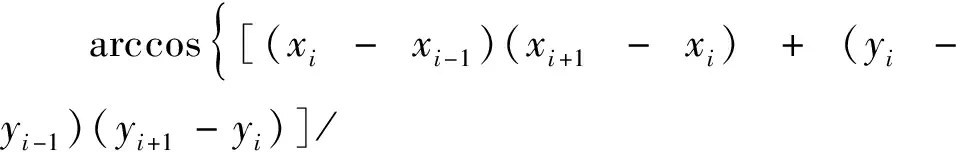
0≤α≤αmax

(7)

式(7)中:αmax為最大偏航角。

(3)最大航程約束。

受無人機續航能力的限制,飛行距離與最大航程為Lmax滿足式(8)的約束。

L≤Lmax

(8)

(4)飛行高度約束。考慮城市無人機空域政策以及安全性,執行配送任務的無人機高度需要限制在最小飛行高度zmin以及最大飛行高度zmax之間。無人機飛行高度的約束關系為

zmin≤z≤zmax

(9)

(5)最大俯仰角約束。無人機在垂直方向俯仰角,是決定路徑可行性的另一個重要參數。該項約束為

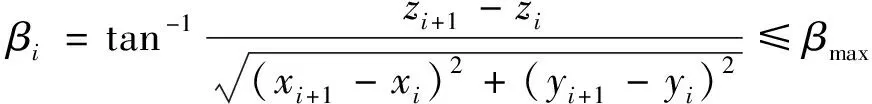
(10)

式(10)中:βi為無人機在第i個路徑節點俯仰角;βmax為無人機最大俯仰角,i=1,2,…,N+1。

3 粒子群優化算法

3.1 標準粒子群算法

標準粒子群算法(standard particle swarm optimization,SPSO)的每個粒子都有一個適應值,還有一個速度決定其飛翔方向和距離。算法隨機產生初始粒子,然后通過迭代更新尋找最優解。假設有N個粒子在D維的搜索空間,即粒子群的種群規模為N,其中,第i個粒子可以表示為xi(t)={xi1(t),xi2(t),…,xiD(t)},根據適應度值來判斷這個粒子是否比當前最優粒子更優。

第i個粒子目前個體最優值位置參數為pbest={pi1,pi2,…piD},種群最優值位置參數為gbest={pg1,pg2,…pgD},速度為vi(t)={vi1(t),vi2(t),…,viD(t)}。第i個粒子第t次迭代時,按照式(11)進行速度和位置的更新。

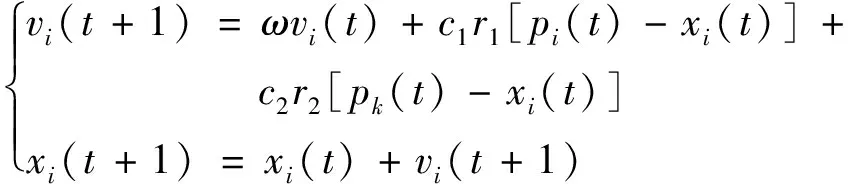
(11)

式(1)中:t為迭代次數;ω為慣性權重;c1和c2為加速因子,用于調整粒子的位置,向潛在的最優位置靠近,反映粒子自身和整體學習能力;r1、r2為分布在(0,1)中的兩個隨機數,用于增加粒子的容錯性和尋優能力,表明算法在搜索全局最優解時具有隨機性。粒子更新速度vi通常受[-vmax,vmax]的限制,vmax為最大更新速度。

為加速群體收斂,目前大多采用線性遞減策略得到慣性權重值,即

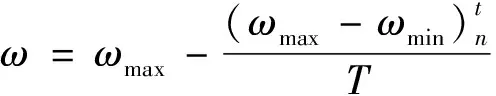
(12)

式(12)中:ωmax和ωmin分別為設定的最大、最小慣性權值;t、T分別為當前迭代次數和最大迭代次數。

3.2 綜合改進的粒子群優化算法

為快速獲得全局最優解,對SPSO進行了改進,包括引入Singer映射改進粒子初始分布、線性調整加速因子和最大速度、位置更新策略,及自適應調整慣性權值,從而構建綜合改進的粒子群優化算法(comprehensive improved particle swarm optimization algorithm,CIPSO)。

3.2.1 混沌初始化

初始粒子的分布質量對尋找最優解起著至關重要的作用。初始分布越均勻,粒子種群的多樣性越豐富,獲得最優解的機會越大,收斂速度越快。一些研究者提出了基于混沌的粒子群初始化方法[10]。混沌系統于20世紀60年代被美國氣象學家首先發現,因其具有廣泛的隨機性、遍歷性、復雜性的特點被廣泛應用[11],適于描述復雜的路徑隨機尋優。相較于隨機初始化,混沌初始化是一種強大的分散群的策略,可以豐富粒子種群多樣性,提高算法的尋優和收斂性能。Singer模型是產生混沌序列的常見模型,本文研究應用Singer模型初始化粒子種群,如式(13)所示,其中參數由經驗法或者試錯法確定,本文參數沿用文獻中常用數據[12],經過仿真實驗證明其提高了粒子群算法的性能。

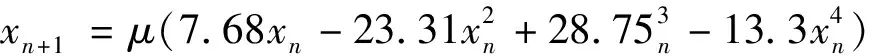
(13)

式(13)中:μ為取值在[0.9,1.08]控制系數;xn為第n個混沌變量。

3.2.2 線性調整加速因子

加速因子c1、c2通常被設置為常值,但是從群體評價的角度來看,如果能自適應地調整,算法可以保持更好的性能。采用線性方法計算加速因子,即

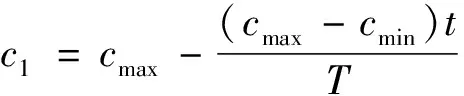
(14)

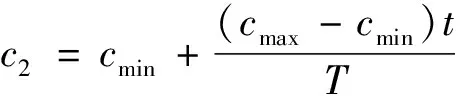
(15)

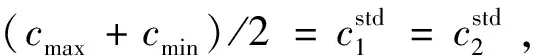
3.2.3 線性調整粒子最大速度

通常將最大速度vmax作為定值,不能準確反映搜索的多樣性和精度。應用線性調整策略來計算vmax即

(16)

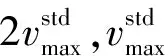
3.2.4 位置更新

為提高收斂速度,本文研究提出一種新的位置更新策略。首先,執行一次SPSO算法,按照粒子適應度值由小到大重新排列。然后,根據式(17)和式(18)進行位置更新。

Plarge=Psmall+ar3

(17)

vlarge=vsmall

(18)

式中:Plarge為適應度值較大的一半粒子;Psmall為適應度值較小的一半粒子;r3為[0,1]中的隨機數;a為位置更新常數,反映新突變粒子對適應度值小的粒子的位置偏移程度。

3.2.5 自適應調整慣性權值

慣性權值對算法全局尋優能力起著至關重要的作用。本文算法的慣性權值隨著迭代次數的增加動態調整,從而避免陷入局部最優。動態調整的慣性權值為

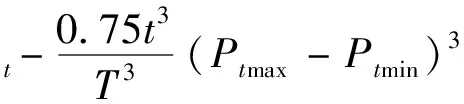
(19)

式(19)中:Ptmax為當前迭代次數下粒子群中最大適應度值;Ptmin為當前迭代次數下粒子群中最小適應度值,?t為當前迭代次數下粒子群慣性權值。

3.3 算法流程

步驟1獲取城市低空環境數據,采用非二值存儲法生成柵格危險度因子矩陣。

步驟2對無人機進行PSO參數初始化,包括粒子維數D,慣性權重w,加速度因子c1、c2,最大速度Vmax,最大迭代時間T,按式(13)進行粒子群初始化。

步驟3通過式(2)～式(5)構造各無人機的適應度函數并執行一次粒子群算法。

步驟4計算適應度函數,確定粒子最佳位置。

步驟5根據設計的策略更新參數,通過式(13)進行粒子群初始化;通過式(14)和式(15)更新加速度系數c1、c2;通過式(16)更新最大速度Vmax;通過式(19)更新慣性權值w。

步驟6根據式(17)和式(18)對所有粒子的適應度值進行排序,更新粒子位置。

步驟7優化改進的PSO算法,并重復步驟4～步驟6,直到滿足最大迭代次數。

步驟8輸出最優路徑。

4 仿真分析

選擇天津市五大道風景區周邊作為無人機路徑規劃背景,衛星圖和模擬圖如圖2所示。

4.1 仿真環境與參數設置

利用Google Earth獲取天津五大道風景區周邊地理高程數據,并用Arcgis將要素轉化為柵格,作為無人機飛行環境。部分環境高程數據如表1所示,部分參數值參照文獻[13]設置,如表2所示。

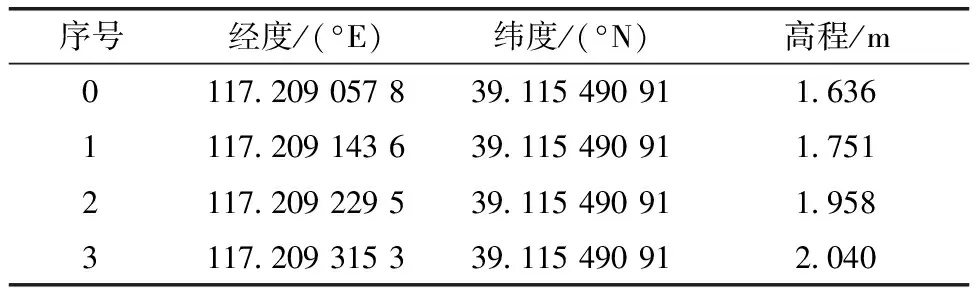
表1 環境數據

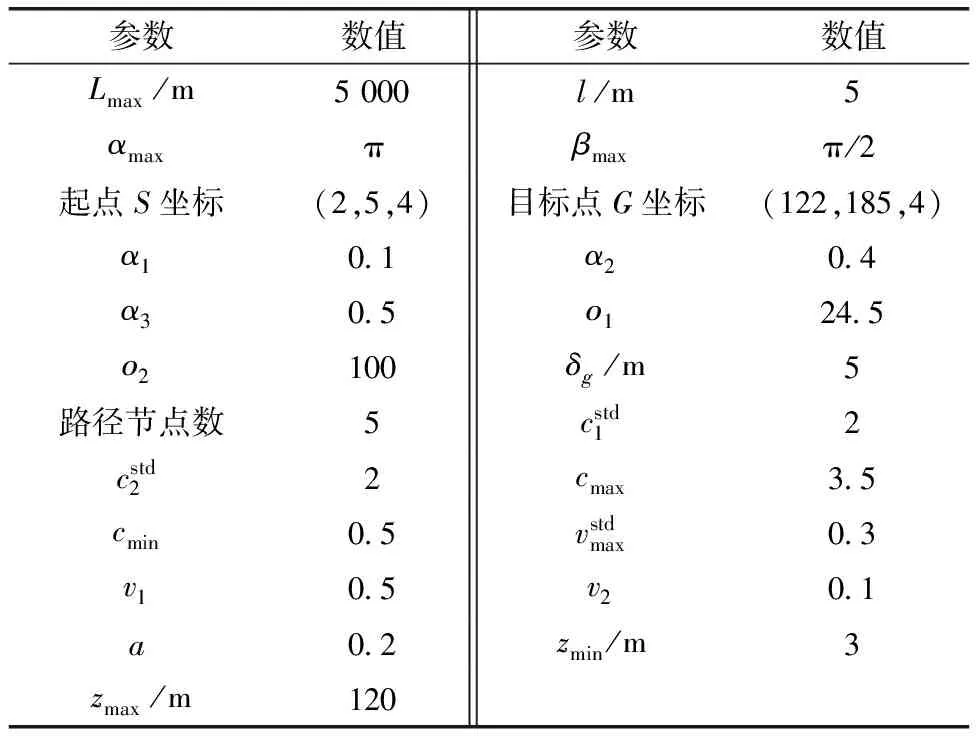
表2 參數設置

4.2 仿真結果分析

實驗中采用5種優化算法,分別是SPSO、線性改進加速因子粒子群優化(improved acceleration coefficients particle swarm optimization,ICPSO)、線性改進最大速度粒子群優化(improved velocity particle swarm optimization,IVPSO)、混沌粒子群優化(chaotic particle swarm optimization,CPSO)、CIPSO。5種優化算法均在路徑曲線上獲取5個路徑節點,參數設置、路徑規劃環境保持不變,得到的路徑規劃結果如圖3所示。從路徑長度、柵格危險度、高度代價以及總代價進行分析,結果如表3所示。

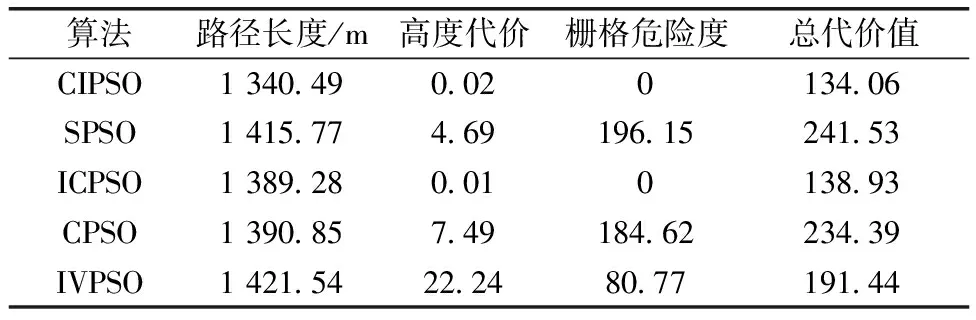
表3 物流無人機路徑規劃結果評價值

從表3可以看出,CIPSO在路徑長度、高度代價、柵格危險度以及總代價值4個方面均取得了更優的結果。ICPSO在路徑長度、總代價值取得了僅次于CIPSO的結果。IVPSO的路徑高度變化以及路徑長度最大。SPSO的柵格危險度和航路總代最大。可見,CIPSO算法用于無人機路徑規劃是可行的和有效的。

4.3 參數敏感性分析

在路徑規劃過程中,柵格像元粒度大小、代價函數權重系數{α1,α2,α3}以及航路點個數會對結果產生重要影響。下文對各個參數的敏感性進行分析。

4.3.1 柵格粒度大小分析

柵格像元粒度,即柵格的邊長,分別取5、10、15、20、25 m,其他參數保持不變,進行多組實驗,具體結果如表4所示,代價函數與柵格像元粒度大小變化如圖4所示。

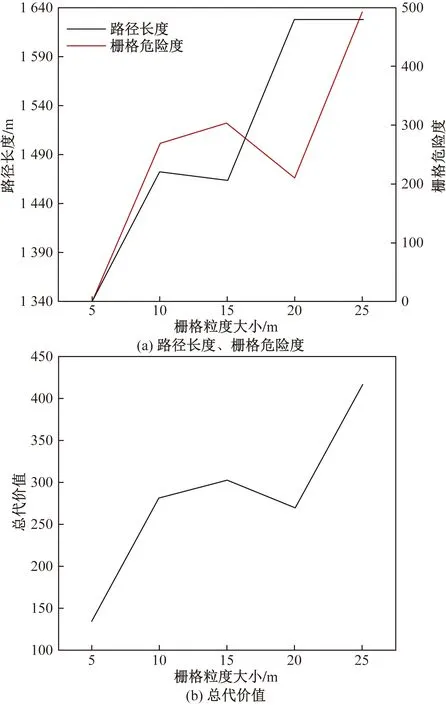
圖4 柵格像元粒度大小對無人機運行的影響

從表4中可以看出,當柵格像元粒度為5 m時,無人機路徑長度達到最小值1 340.49 m,柵格危險度達到最小值0,總代價值達到最小值134.06。當柵格像元粒度在5～25 m時,隨著像元粒度的增大,路徑長度和柵格危險度波動增大。高度代價在不同的柵格像元粒度大小下波動在一個較低的水平,并在柵格粒度為5 m時達到最小值。綜合平衡各路徑代價,像元粒度選取5 m最優。

此外,高度代價在實驗中波動較大。在參數設置合適情況下,無人機能夠維持在一個穩定的高度上,而當參數動態經過某一的臨界點后,無人機將發生劇烈的高度變化。

4.3.2 權重系數分析

為滿足安全要求,保持柵格危險度系數α3不變,分析α1和α2取值的影響,其余參數如表2所示。各組實驗結果如表5和圖5所示。

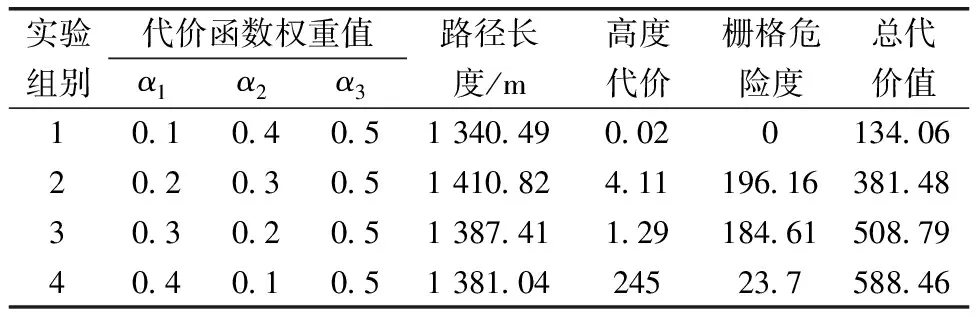
表5 不同代價函數權重的影響

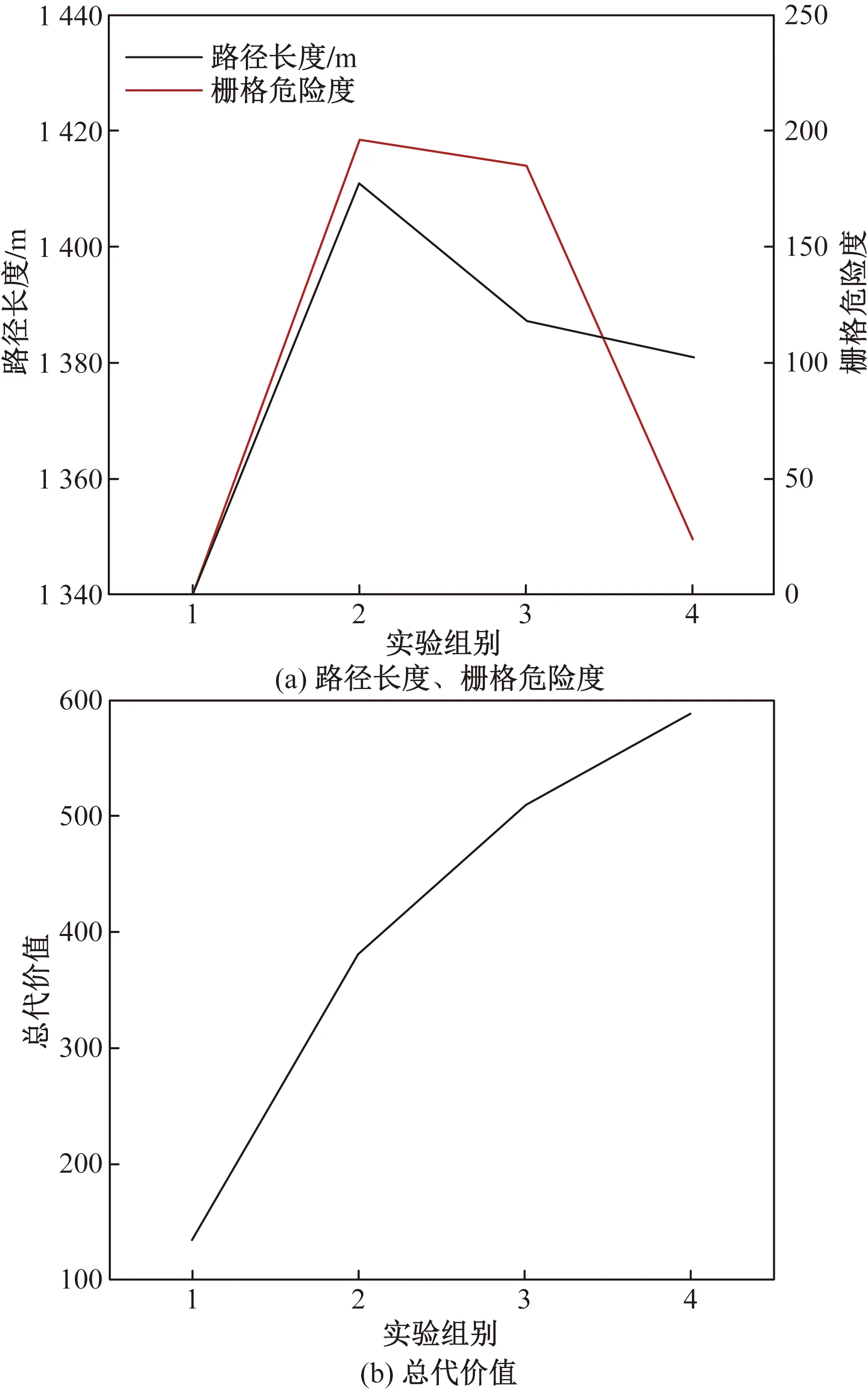
圖5 代價函數權重值的影響

由表5可知,路徑規劃結果隨代價權重值取值不同有明顯變化。隨著路徑長度代價權值α1的增大,路徑長度波動在一個穩定區間內,而路徑總代價值呈增大的趨勢。隨著高度代價權值α2的下降,高度代價先趨于穩定在一個較小的值,當α1=0.4,α2=0.1時,高度代價達到了一個較大的值。當α1=0.1時,柵格危險度代價達到最小值,當α1=0.2或0.3時波動到較大值。綜合平衡各路徑代價,選擇α1=0.1,α2=0.4和α3=0.5。

4.3.3 路徑節點個數分析

為進一步說明選取的路徑節點個數對規劃路徑精細度的影響,分別選取5～13個路徑節點進行仿真。對各組實驗結果如表6和圖6所示。

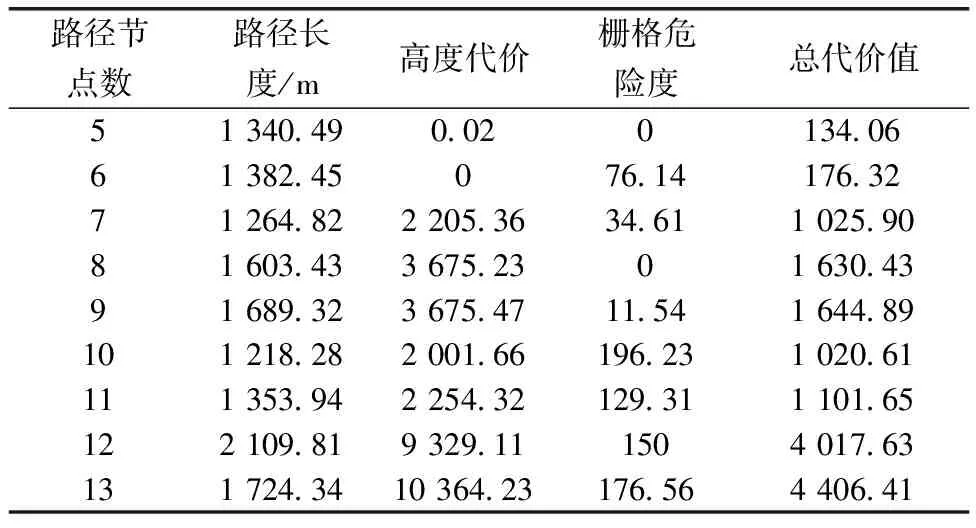
表6 路徑節點個數對代價函數影響

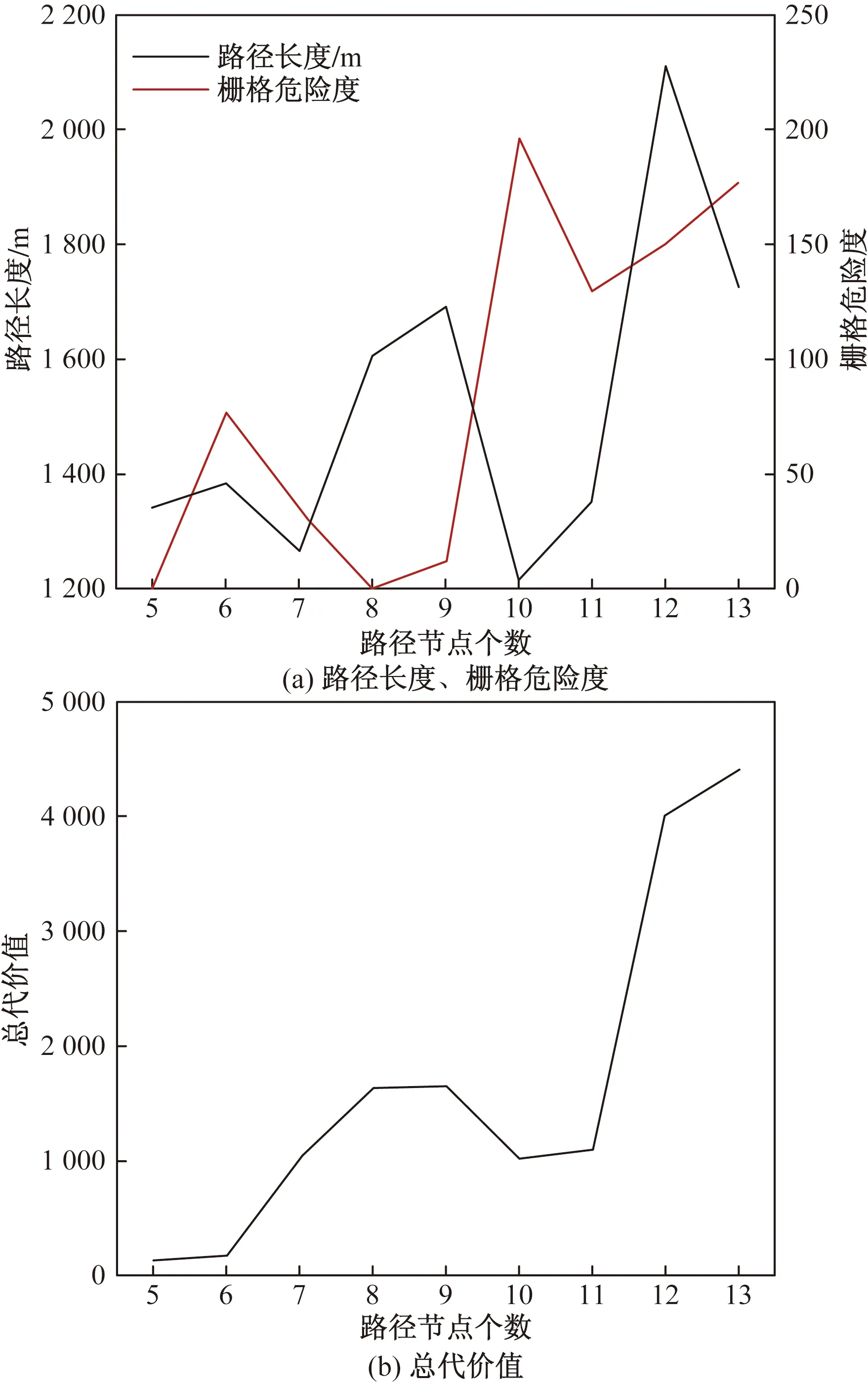
圖6 路徑節點個數對無人機運行的影響

由表6可知,隨著路徑節點數量的增加,路徑長度、柵格危險度以及總代價在波動中有增加趨勢。高度代價先保持在穩定且較小的數,當路徑節點達到7個時迅速增加。綜合平衡各路徑代價,選擇路徑節點個數為5。

5 結論

設計了考慮路徑長度、高度變化以及柵格危險度的多目標,引入了無人機自身性能約束,建立多目標、多約束的物流無人機路徑規劃模型,并采用改進的粒子群優化算法求解模型,得出以下結論。

(1)本文多目標模型和CIPSO算法,能夠規劃在路徑長度、高度變化和安全性這三方面更優的路徑,應用于物流無人機的路徑規劃是可行的和有效的。

(2)柵格像元粒度大小、權重系數、路徑節點數對算法有較大的影響。在本文算例中,當柵格粒度取5 m,路徑節點取5個,α1=0.1,α2=0.4,α3=0.5時,路徑規劃總代價最佳。

本文研究了單無人機靜態路徑規劃,今后將會對無人機動態路徑規劃、多無人機協同路徑規劃展開研究。