郵輪多孔型組合密集開孔梁結構極限承載能力研究

方治臻，周 宏，葛 席，彭 帥

(江蘇科技大學 船舶工程學院，江蘇 鎮江 212003)

0 引 言

開孔梁在豪華郵輪上層建筑中作為主要承重結構之一，研究開孔對強梁極限承載能力的影響有助于大型郵輪建造技術的發展，加快國內大型郵輪設計慣例的形成。

開孔梁一般會受到艙外水壓力、貨物重量、人員重量、設備重量，船底梁還會收到上層建筑的部分重量。因此開孔梁在郵輪的實際承載情況中受到2 個方向上的力，一個是軸向的力，另一個是橫向垂直于甲板的力。徐秉漢等[1–4]將解析分析與有限元數值分析相結合，研究了船舶縱桁和橫梁腹板上開圓孔和腰圓孔后的應力集中問題，提出了用于梁結構應力集中的局部應力分析法。黃倩等[5]分析了腹板開孔船體梁的失效過程，吳言亮[6]研究了工字型梁腹板開孔后采用套管加強的承載能力計算方法，最終給出了工字型鋼梁腹板開孔時采用套管加強結構加強的整體結構承載力計算公式。周艷秋[7]使用Ansys 建立了腹板開孔梁有限元模型，將許用應力作為閥值，探討腹板開孔對梁模型最大應力值影響。Park 等[8–11]提出了帶腹板開孔的肋板組合梁極限強度的計算方法，Ehab Ellobody 等[12–14]通過Ansys、Abques 等有限元軟件，研究了開孔梁的失效模式和開孔高度、寬度、位置、形狀的關系，并分析了開孔2 個和3 個孔時的極限承載能力和開孔的失效模式。

綜上所述，目前開孔梁的研究中絕大部分還處在單一橫向載荷對極限承載能力的影響，少部分研究中加入了雙軸載荷，但沒有考慮到軸向載荷的變化對極限承載能力的影響。除此之外，對于開孔的單一孔型研究較多，密集開孔的研究較少。而且由于船型特殊構件的開孔以及設備貫穿孔的尺寸經常會超出現有規范，但目前超規范開孔國內外的研究成果較少。本文通過Ansys 的非線性屈曲分析，研究郵輪多孔型組合密集開孔梁結構的極限承載能力，并考慮在最切合實際工況的雙軸載荷下研究梁的極限承載能力的變化，探究失效模式和開孔參數之間的關系，結合有限元分析結果整合現有的各國開孔梁的相關規范，為多孔型密集開孔的強梁構件提供開孔尺寸和位置的參考。

1 非線性屈曲極限載荷計算方法

綜合目前國內外對開孔梁結構極限承載能力的評估方法，本文采用特征值屈曲結合非線性屈曲的有限元法計算極限載荷，具體方法如下：

1）進行特征值屈曲分析，在線性情況對結構進行求解本身屬于前屈，特征值屈曲求解利用了線性系統的剛度矩陣。當矩陣發生奇異時讀出奇異矩陣的特征值，得到開孔結構的屈曲模態，通過負載乘數計算特征值屈曲分析下的極限載荷，此時不考慮所有非線性因素（材料非線性、大撓度、初始缺陷）。

2）進行非線性屈曲分析，修改模型添加非線性屬性（材料非線性、大撓曲，以及初始缺陷），分析具有初始缺陷的結構在理想載荷路徑下的非線性屈曲和計算其彈塑性效應。由于非線性屈曲分析同時考慮到了材料非線性、幾何非線性、初始缺陷，因此，非線性屈曲能夠模擬結構最真實的工況，以更接近結構的真實極限承載能力。

3）修改模型載荷將特征值屈曲分析中的極限載荷，放大到1.2 倍作為非線性屈曲分析的載荷進行加載。同時讀取第一階屈曲模態變形，將模態變形的1‰作為初始變形添加為初始缺陷。

4）利用Ansys 非線性求解器，進行非線性屈曲分析，利用時程后處理器，提取腹板開孔后結構的極限承載力結果，讀取極限載荷時應當以不收斂的前一步作為最終結果，繪制載荷-位移圖。有限元計算流程如圖1 所示。

圖1 非線性屈曲分析極限承載能力計算流程圖Fig.1 Calculation flow chart of ultimate bearing capacity of nonlinear buckling analysis

2 模型及邊界條件設置

某大型豪華郵輪，縱桁強梁上下兩端分別布置支柱支撐，選取該模型為研究對象，甲板板厚度為6.5 mm。為保證中性軸處在幾何中心的位置，甲板帶板的寬度選擇185 mm，T 型梁腹板高度為450 mm、厚度為8 mm，下翼板寬度為120 mm、厚度為10 mm。材料選擇CCS 規范中的船用高強度結構鋼AH36，泊松比0.3，屈服強度為355 MPa。

根據參考規范中錯位支柱的邊界條件，本模型邊界條件選取為左端限制x、y、z方向上的位移，并釋放轉角。右端釋放徑向位移，并釋放3 個方向上的轉角，如圖2 所示。

圖2 結構坐標系示意圖Fig.2 Structure coordinate system diagram

2.1 網格無關性驗證

通過LR 和CCS 郵輪局部結構計算指南規范，需對未開孔模型進行網格無關性驗證。細網格分析是網格尺寸大于板厚t×t，小于50 mm×50 mm。整體板厚最薄為6.5 mm，因此網格無關性驗證的網格尺寸分別設置為10 mm×10 mm、15 mm×15 mm、20 mm×20 mm、25 mm×25 mm、30 mm×30 mm、35 mm×35 mm、40 mm×40 mm。此處采用shell 單元建模。根據對整體結構的特征值屈曲分析發現第1 階模態結構已經發生屈曲，選取第1 階模態所得屈曲載荷的1.2 倍作為非線性屈曲的極限載荷進行加載。

如圖3 所示，單元尺寸降到15 mm×15 mm 時，載荷-位移曲線開始趨于穩定，如果繼續減少單元尺寸繼續減小對結果影響不大，而且會加大有限元計算的時間，因此將后續有限元分析單元尺寸選定為15 mm×15 mm。

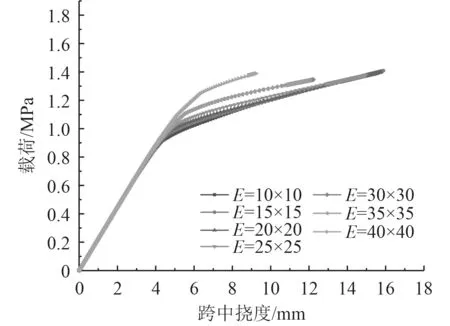
圖3 網格無關性驗證Fig.3 Grid independence verification

2.2 多孔型組合密集開孔分組

根據對單一開孔、單一密集開孔的有限元分析，圓孔和腰圓孔可能在同樣位置造成不同的破壞模式，而通過對比跨中開圓孔、跨中開腰圓孔和矩形圓角孔3 種結構的分析結果發現，在開孔面積一致時跨中開腰圓孔和矩形圓角孔的結構對極限承載能力的削弱更小同時可獲得更多的開孔寬度，但跨中開圓孔可獲得更高的開孔高度。因此針對不同孔型組合的有限元分析將單一密集開孔的部分結構作為對照組，設置3 組有限元分組。

分組如下：第1 組為單一孔型；第2 組為2 孔型；第3 組為3 孔型。每一組內分別設置不同對照組。每組內設置有限元參數為開孔高度D。具體有限元分組如圖4～圖13 所示。S 代表分組二中對稱布置的孔型組合，NS 代表非對稱孔型組合。分組1 記為A 組，分組二記為B 組，分組3 記為C 組。

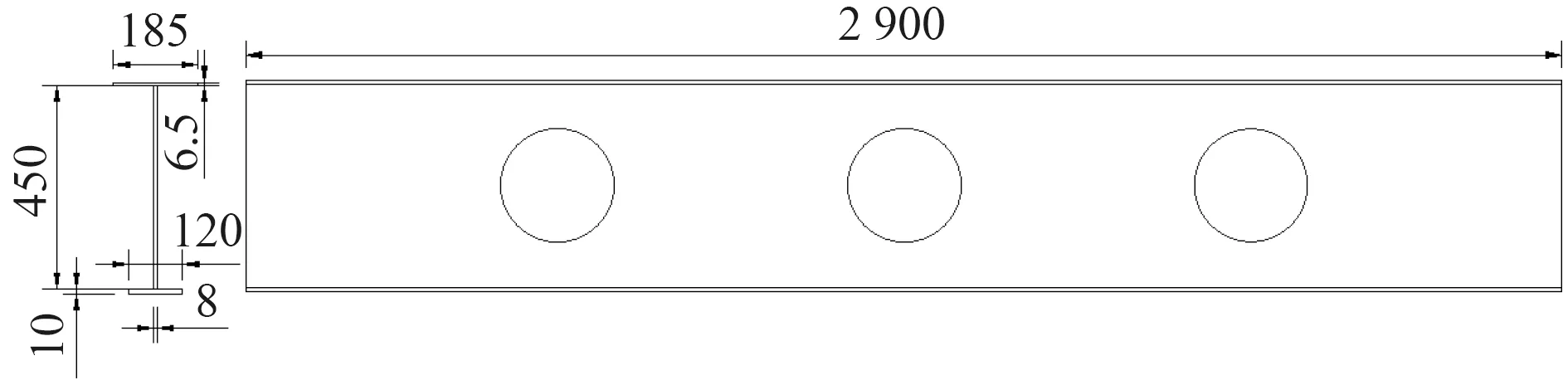
圖4 A-1 孔型示意圖Fig.4 A-1 hole diagram

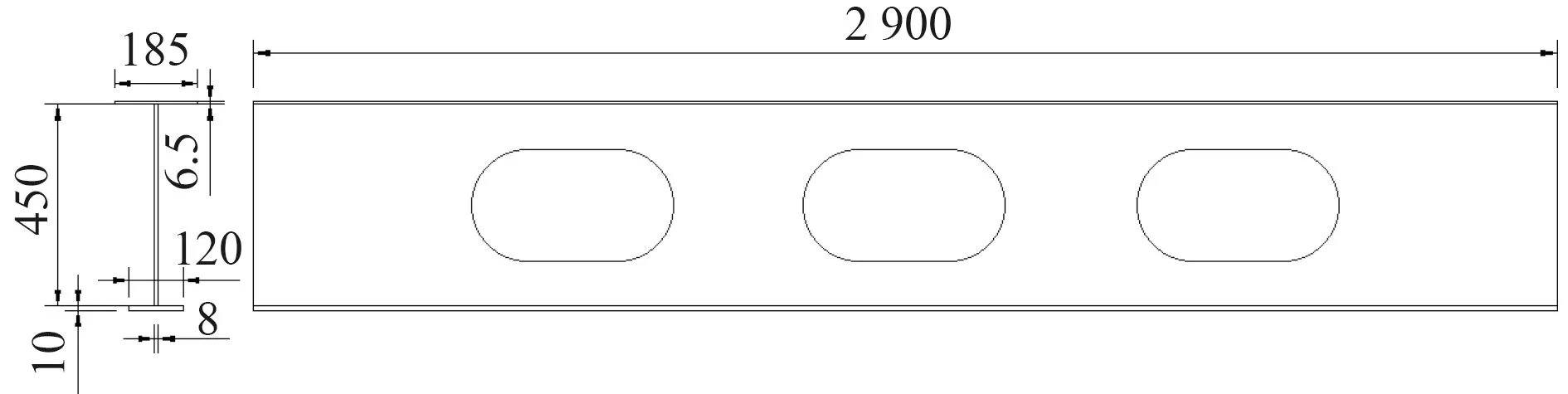
圖5 A-2 孔型示意圖Fig.5 A-2 hole diagram

圖6 A-3 孔型示意圖Fig.6 A-3 hole diagram

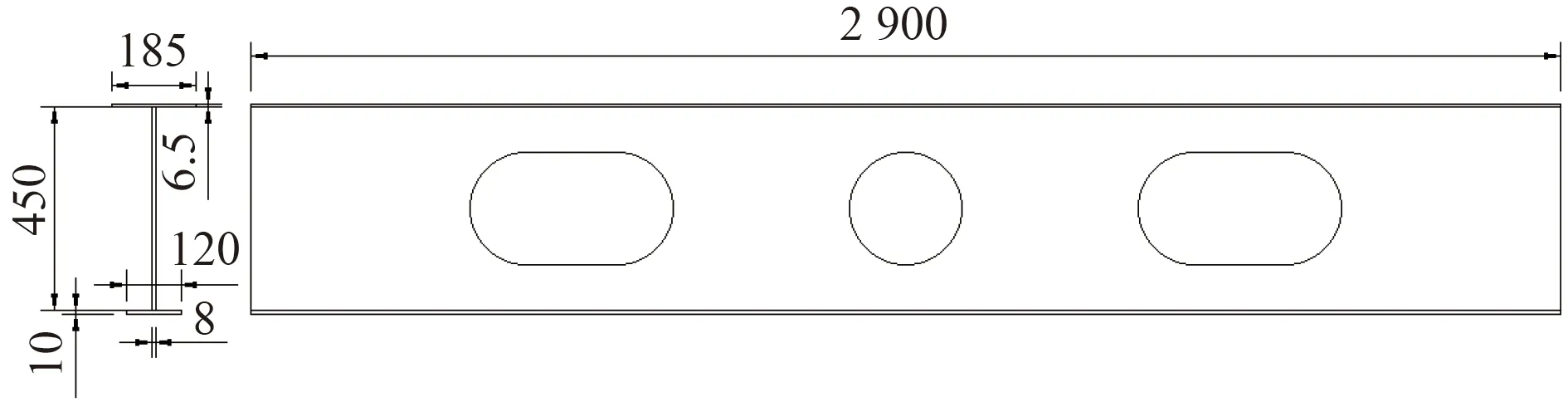
圖7 B-S-1 對稱性開孔布置1Fig.7 B-S-1 hole diagram

圖8 B-S-2 對稱性開孔布置2Fig.8 B-S-2 hole diagram

圖9 B-NS-1 非對稱性開孔布置1Fig.9 B-NS-1 asymmetric opening arrangement 1

圖10 B-NS-2 非對稱性開孔布置2Fig.10 B-NS-2 asymmetric opening arrangement 2

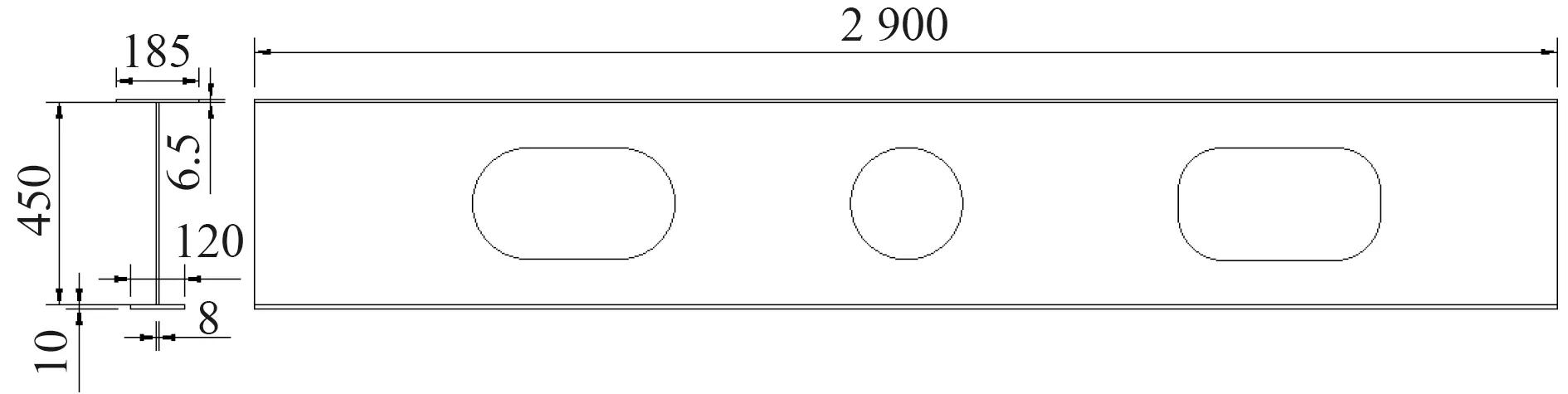
圖11 C-NS-1 非對稱性開孔布置1Fig.11 C-NS-1 asymmetric opening arrangement 1

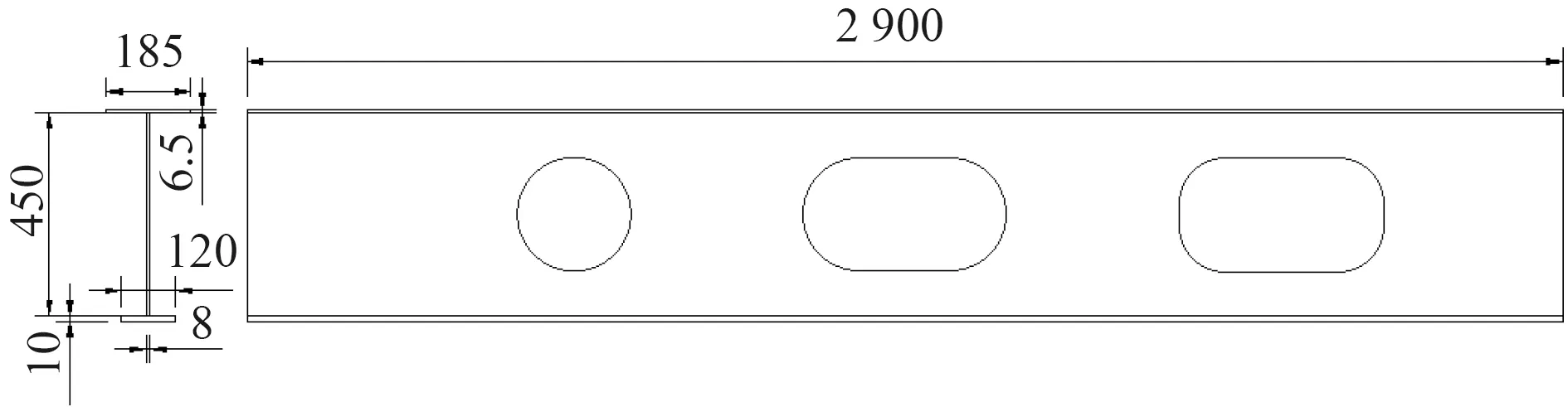
圖12 C-NS-2 非對稱性開孔布置2Fig.12 C-NS-2 asymmetric opening arrangement 2

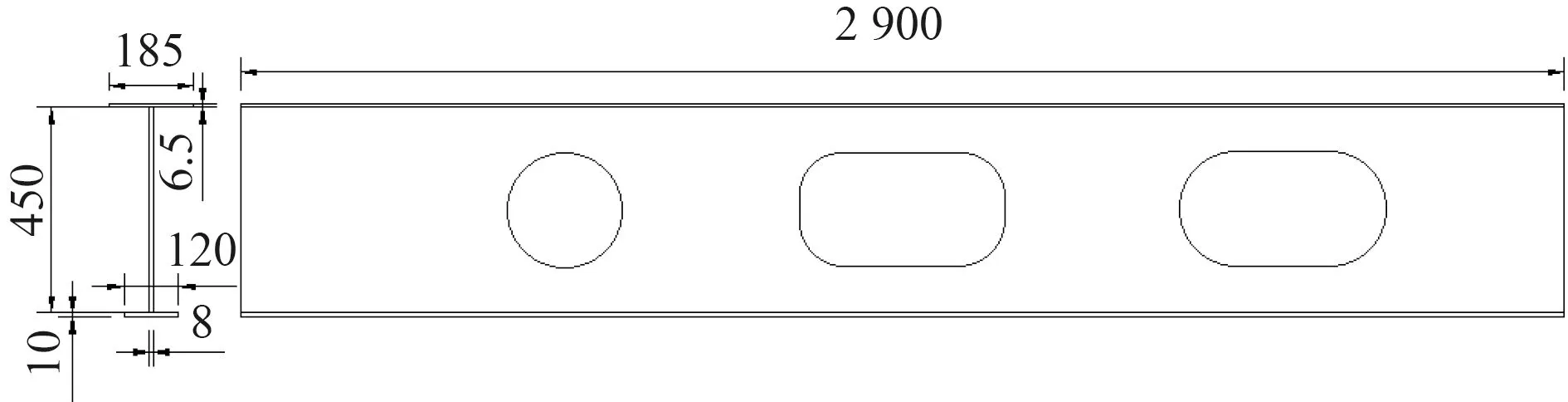
圖13 C-NS-3 非對稱性開孔布置3Fig.13 C-NS-3 asymmetric opening arrangement 3

根據對某大型郵輪的強梁開孔統計，強梁開孔高度已達55.56%，已經超過規范的要求。而通過對單一孔型密集開孔的極限承載能力分析，當開孔較大分布在梁結構1/3 和2/3 的位置對極限承載能力的影響相對較小，而開腰圓孔和矩形圓角孔的寬高比在2 時，比較合適。因此將開孔中心選定在1/3 位置處，以開孔高度為單一變量，開孔寬度設計為2 倍的高度，這是不超過規范的寬高比，也是目前研究文獻中推薦的寬高比。腰圓孔圓角尺寸選擇根據某大型郵輪腰圓孔圓角半徑尺寸統計而來，選擇為0.4D。矩形圓角孔圓角半徑尺寸根據幾何關系可知為0.5D。具體分組如表1所示。

表1 有限元分組Tab.1 Finite element grouping

3 有限元結果及分析

為更傾向于符合大型豪華郵輪設計建造實際情況，從抗彎極限承載能力、抗壓極限承載能力、以及彎+壓3 個角度對比分析不同孔型組合的極限承載力，判斷不同孔型組合在實際工程中適用的位置，未開孔時的極限承載力為1 308 900 N。為了方便有限元分組更清晰地表達不同開孔參數對強梁極限承載能力的影響，引入無因次量Qult/Qult，0。其中Qult為開孔后的強梁極限強度，Qult，0為未開孔情況下強梁的極限強度，對有限分組結果繪制點線圖。

3.1 多孔型密集開孔的抗彎、抗壓極限承載能力

由圖14 可知，在同一開孔高度下，3 種分組的抗壓極限承載能力明顯大于對應的抗彎極限承載能力，說明多型密集開孔對橫向極限承載能力造成了較大的損失；開孔高度的增加對于抗彎和抗壓極限承載能力有著較大影響。

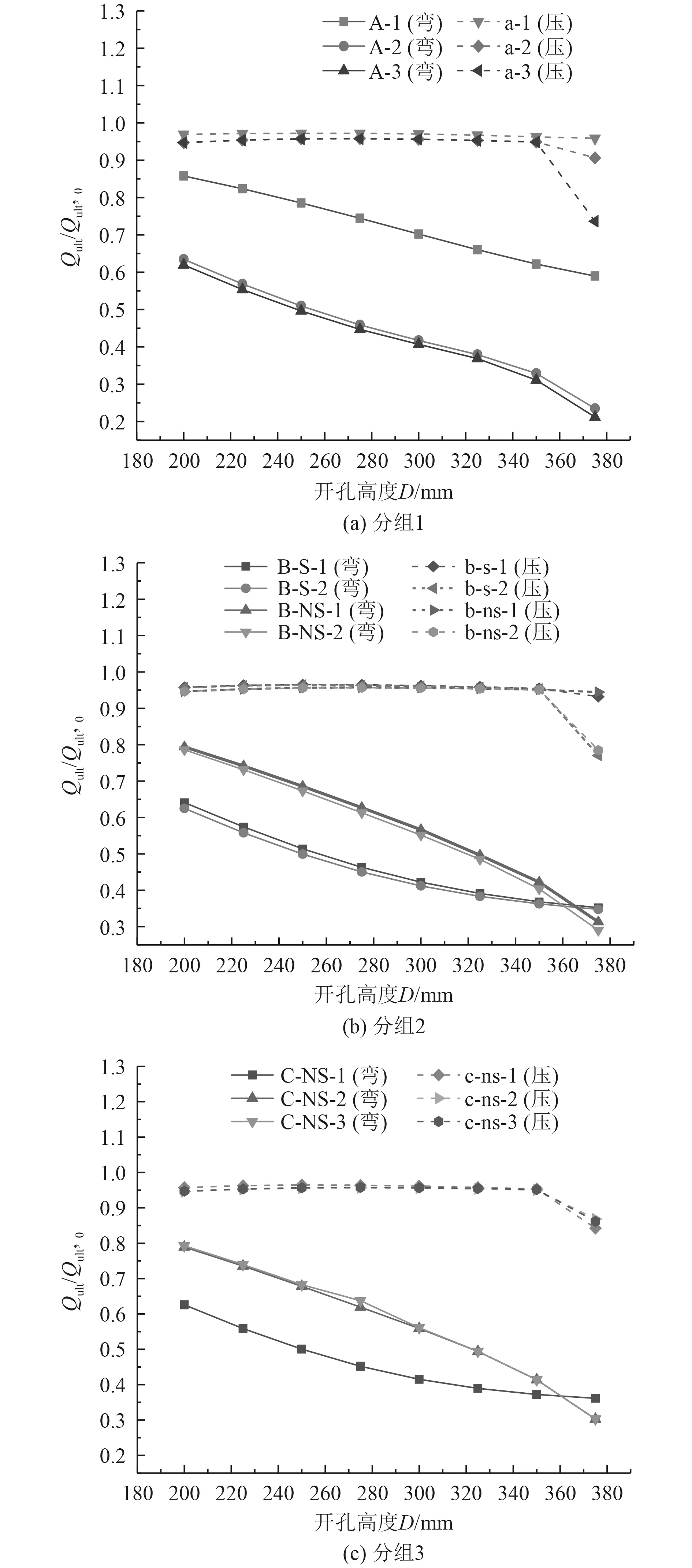
圖14 多孔型開孔的抗彎、抗壓極限承載能力對比Fig.14 Comparison of bending ultimate bearing capacity of different orifices

3.2 多孔型下的抗彎極限承載能力對比

由表2 和圖15 可知，隨著開孔高度的增加，開孔梁的抗彎極限承載能力在不斷減少。通過對比非對稱性開孔（B-NS-1、B-NS-2）和對稱性開孔（B-S-1、BS-2）的4 條曲線可看出，同一開孔高度下的非對稱性開孔的抗彎極限承載能力要大于對稱型開孔。這是因為非對稱性開孔發生破壞時首先產生在靠近左端的圓孔處，而對稱孔型發生在靠近左端的腰圓孔、矩形圓角孔處，此時該處開孔靠近端部，當開孔高度一致時，較大的開孔寬度，使得剪力在開孔處產生的次彎矩大于圓孔，導致極限承載能力被削弱的較多。因此在考慮多孔型開孔時如果實際情況要求靠近端部，在端部開圓孔要優于其他孔型。

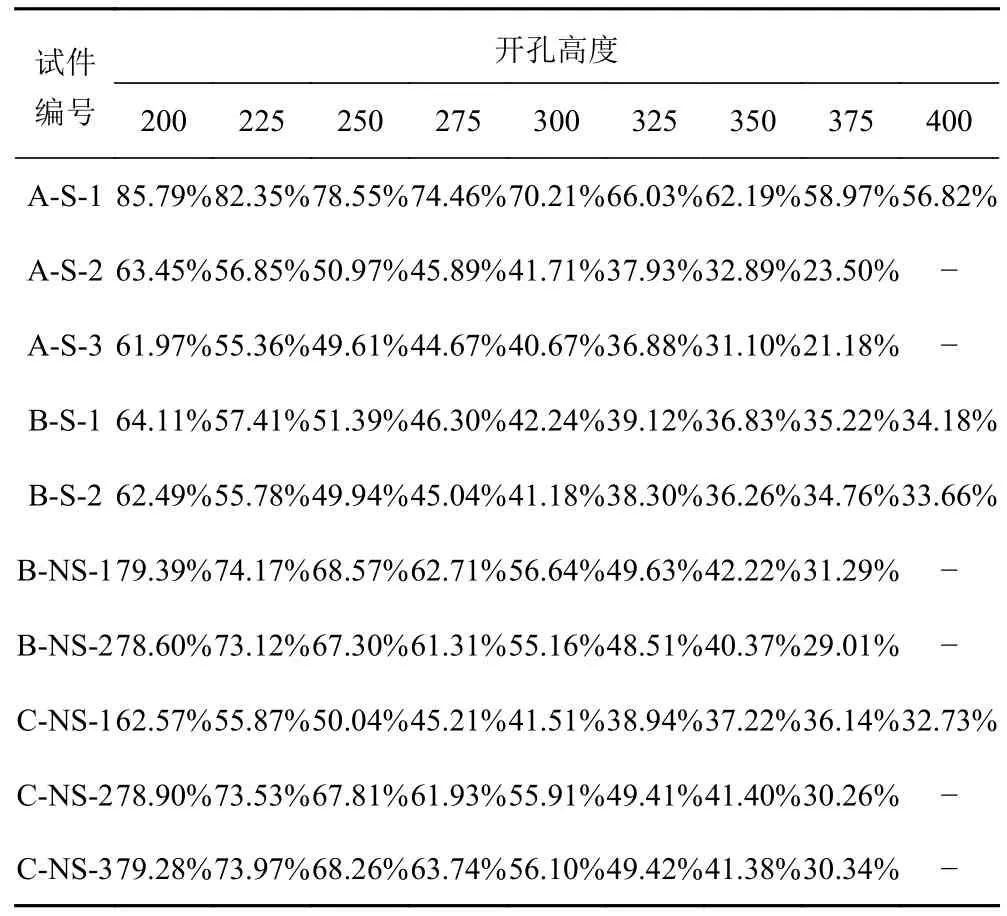
表2 抗彎極限承載能力計算結果Tab.2 Calculation results of bending ultimate bearing capacity

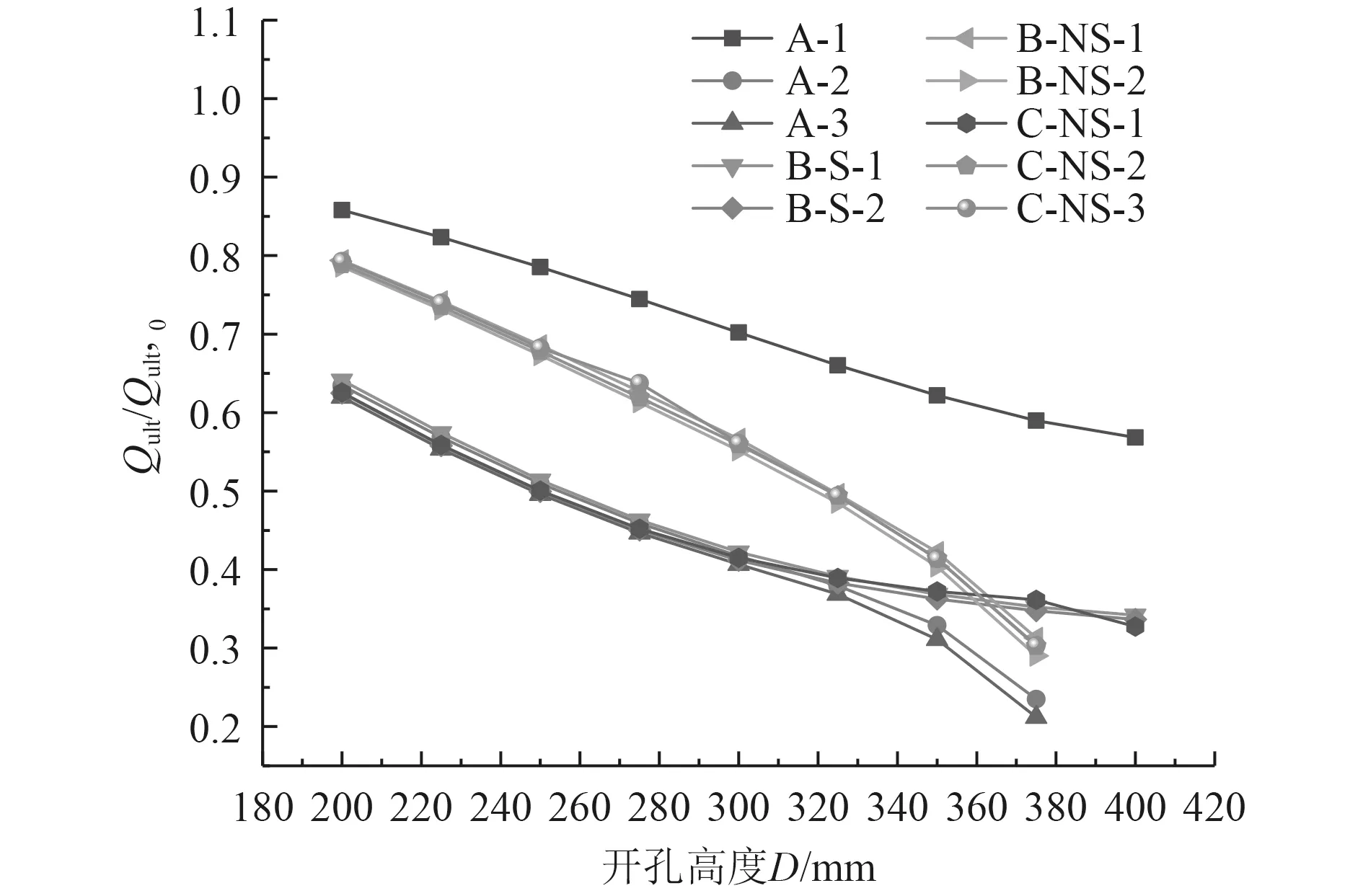
圖15 多孔型組合開孔的抗彎極限承載能力對比Fig.15 Comparison of flexural ultimate bearing capacity of different openings

從圖15 可看到，在開孔高度小于300 mm 時，A-2、A-3、B-S-1、B-S-2 和C-NS-1 共5 條曲線相似且幾乎重合，說明0.4D的圓角半徑對極限承載能力的影響較小。當開孔高度大于300 mm 時，其抗彎極限承載能力曲線出現了分叉點，可看出A-2、A-3 孔型不推薦開超過300 mm 的孔。B-NS-1、B-NS-2、C-NS-2、C-NS-3 這4 條曲線重合，但由于C 組開孔為3 孔型，施工難度增加，因此不推薦。

3.3 多孔型下的抗壓極限承載能力對比

由表3 和圖16 可知，多型密集開孔對軸向極限承載能力的影響并不明顯，但當開孔大于350 mm 時，卻會對軸向極限承載能力造成嚴重損失，因此開孔大高度不應超過350 mm。而結合相關開孔規范和文獻分析可得，在結構橫向三等分點位置附近，軸向開孔的孔型已經不會對軸向極限承載力造成擾動。

表3 抗壓極限承載能力計算結果Tab.3 Calculation results of compressive ultimate bearing capacity

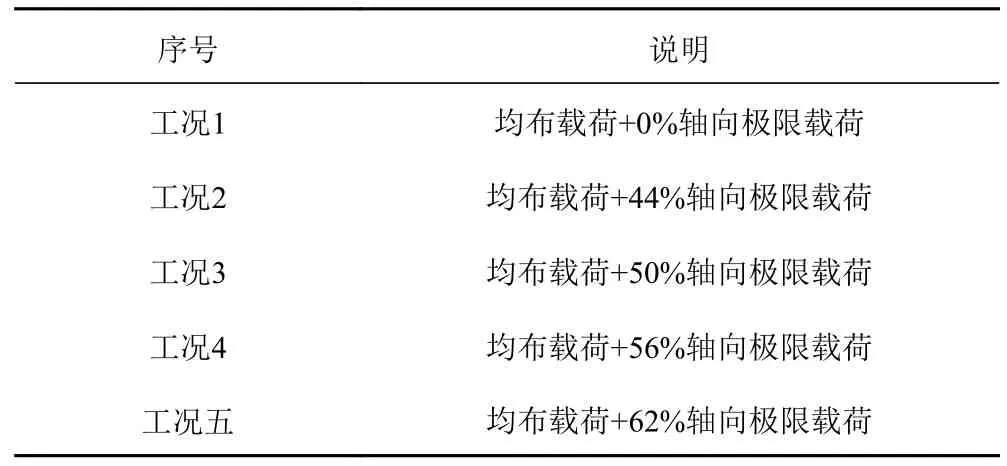
表4 彎+壓載荷下的工況Tab.4 Working conditions under bending + compression load

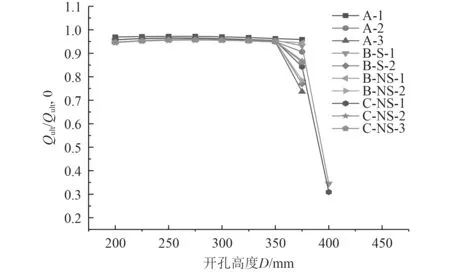
圖16 多孔型組合開孔的抗壓極限承載能力對比Fig.16 Comparison of compressive ultimate bearing capacity of different openings

3.4 聯合載荷作用下的載荷-位移對比

根據分析可得，開孔最大高度不應超過350 mm，開孔中心分布在三等分點位置時較為理想。因此基于此條件對分組1 和分組2 進行雙軸壓縮工況下的極限載荷分析。

由圖17 可知，在彈性階段，軸向載荷對結構整體的極限承載能力影響并不明顯，但在塑性階段會使開孔周圍加快局部屈曲，極限承載能力會提前下降，其中開腰圓孔和矩形圓角孔更為明顯。而三圓孔的開孔梁節點在承受雙軸壓縮時，對極限承載能力的影響不大。

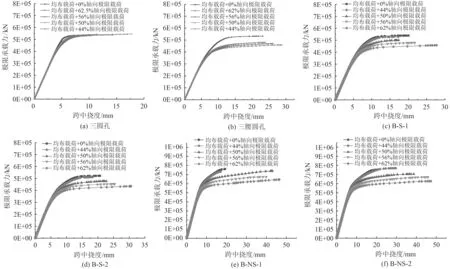
圖17 考慮軸向載荷的極限承載能力分析Fig.17 Ultimate bearing capacity analysis considering axial load

軸向載荷并不會改變均布載荷下的屈曲模式，但會加速甲板帶板或腹板的局部屈曲使多事失效模式形成復合。如圖18 和圖19 所示，開孔梁考慮軸向載荷和不考慮軸向載荷的最終應力云圖和實效變形對比。當開孔分布在三等分點附近附加軸向極限載荷時，總是在遠離加載端出現塑性鉸失效，并且伴隨一定程度帶板屈曲，如圖18～圖21 所示。

圖19 遠離軸向加載端開孔塑性鉸失效孔周應力云圖Fig.19 Stress nephogram of plastic hinge failure hole away from axial loading end

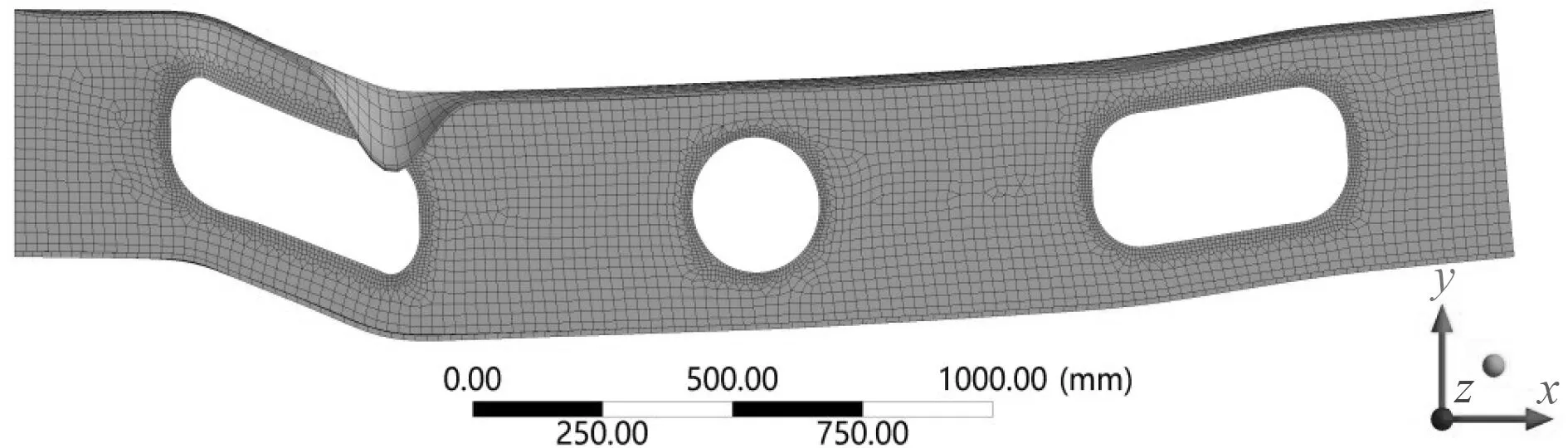
圖20 遠離軸向加載端開孔塑性鉸失效變形圖Fig.20 Failure deformation diagram of plastic hinge with opening away from axial loading end

圖21 遠離軸向加載端開孔塑性鉸失效變形圖Fig.21 Failure deformation diagram of plastic hinge with opening away from axial loading end

綜上所述，離端部較近時布置圓孔要優于其他孔型。當離端部較遠時，開腰圓孔或矩形圓角孔更符合輕量化要求。

4 結 語

本文通過對豪華郵輪多孔型組合密集開孔的開孔梁結構進行Ansys 的非線性屈曲分析，分析10 種不同組合孔型梁的抗彎、抗壓極限承載能力。同時為了考慮軸向載荷對極限承載能力的影響，對比分析了施加不同百分比軸向極限載荷情況下的開孔梁極限承載力。得到以下結論：

1）多型密集開孔對開孔梁結構的橫向極限承載能力造成損失較大，隨著開孔高度的增加這種損失會越來越大，多型密集開孔的高度最大值不能超過350 mm（7/9 腹板高度）。

2）塑性鉸失效和開孔的寬度有很大關系，較大的開孔寬度，使得剪力在開孔處產生的次彎矩更大，導致極限承載能力被削弱的較多。因此在進行多孔型開孔時如果位置靠近端部開圓孔要優于其他孔型，而當開孔位置離端部較遠時，開腰圓孔或矩形圓角孔更符合輕量化要求。

3）軸向載荷對極限承載能力的影響在彈性階段并不明顯，但會使結構提前進入塑性階段，并且當開孔過近時會加速腹板屈曲，當發生塑性鉸失效時會疊加帶板的局部屈曲。