基于EEMD和GA-LSTM算法的行星齒輪故障診斷方法*
陶浩然,許 昕,潘宏俠,*,王 同,徐轟釗
(1.中北大學 機械工程學院,山西 太原 030051;2.中北大學 系統辨識與診斷技術研究所,山西 太原 030051)
0 引 言
行星齒輪傳動是一種多功能的機械傳動方式。該傳動方式可以實現功率分流,具有高效率、高承載能力、高可靠性等優點,是許多旋轉機械設備的一個重要組成部分。然而,由于行星齒輪的齒面幾何形狀非常復雜,行星齒輪的制造和裝配需要很高的精度。另外,行星齒輪經常處于高速和重載等惡劣工況[1],其關鍵部件的損壞都會導致設備的停機,甚至導致嚴重的后果。
因此,研究行星齒輪各振動模式的信號模型[2],保證設備運行的穩定性與可靠性,在實際工程應用中具有重要的意義。
在強烈的背景噪聲下,如何較好地提取行星齒輪的微弱故障特征,這是行星齒輪故障診斷領域需要解決的難題[3]。由于旋轉機械的故障通常伴隨著振動信號的變化,因此,其振動信號分析方法成為故障診斷的有效手段[4]。
針對行星齒輪實際工作條件下,收集到的振動信號的非線性和非平穩性特點,HUANG N E等人[5]提出了一種經驗模態分解(empirical mode decomposition,EMD)算法,由于該算法在處理非線性、非平穩信號上具有自適應等的優點,使得其在一些領域得到了廣泛應用。谷玉海等人[6]對軸承振動數據進行了經驗模式分解和頻譜分析,將頻譜數據壓縮成特征二值化圖像,并將其作為卷積神經網絡的輸入數據進行了訓練,取得了不錯的效果;但使用EMD方法處理振動信號時,容易發生模態混疊的現象。在此基礎上,WU Z等人[7]提出了一種將EMD方法與白噪聲信號的統計特性相結合的新方法,即集合經驗模態分解(EEMD),旨在提高經驗模式分解的準確性和有效性,在特征量提取困難的情況下,利用其自適應性來提取故障特征[8],獲得本征模態函數成分后,直接將其輸入神經網絡,作為特征值[9-10],并根據所需特征用于故障診斷和識別。目前,這種方法已經在故障診斷領域得到了廣泛應用。
在實際工作條件下,收集到的振動信號可能會被各種噪聲源所破壞。針對這一問題,一些學者采用機器學習的方法,對旋轉機械進行了故障診斷。JIN Y等人[11]開發了一種處理一維格式數據的標記序列生成方法,即時間序列變換器,并對其超參數進行了分析,采用該方法進行了滾動軸承故障診斷實驗,對該方法的有效性進行了驗證。
孫燦飛等人[12]采用參數自適應變異模式分解方法,對強背景噪聲下的二階太陽齒輪裂紋進行了診斷;但其特征提取不夠充分。
為了彌補上述方法在特征提取方面的不足,一些學者在故障診斷系統中運用了深度學習方法[13-14]。馮浩楠等人[15]提出了基于批量歸一化的一維卷積神經網絡模型,用于旋轉機械的故障診斷和故障特征的自適應提取,該模型減少了故障診斷的工作量。HUANG W等人[16]使用一種多尺度級聯卷積神經網絡,以端對端的形式,實現了輸入信號分類信息增強的目的,并自適應地提取和識別了故障類型;但是上述方法都沒有考慮故障在時間序列上的特征。
從時間序列數據入手,為提取更全面的故障特征,學者們開始利用長短期記憶(LSTM)網絡。作為一種經改進的遞歸神經網絡,LSTM在時間序列任務中可以更好地捕捉長期依賴關系[17-18],已在很多基于時間序列的應用中取得了不錯的成果。TAK A[19]在輸電系統的故障診斷中,使用LSTM網絡進行了診斷分類。呂云開等人[20]使用孿生神經網絡與LSTM相結合的故障診斷方法,在小樣本數據條件下,取得了不錯的故障診斷效果。
然而,以上學者都未對LSTM網絡的超參數設置產生的影響進行深入研究。
綜上所述,針對行星齒輪工作過程中存在的復雜工況(比如,工作環境差、齒輪輪齒易發生復合故障等),筆者提出一種基于EEMD和LSTM相結合的方法,將其用于行星齒輪故障診斷。
首先,使用EEMD對復雜行星齒輪故障振動信號進行分解,得到其本征模態分量;隨后,將輸入數據送入經遺傳算法優化的LSTM模型中進行訓練,并對網絡超參數進行自動尋優,以提高模型的分類精度和泛化能力;最后,采用4種狀態下采集的行星齒輪故障信號制作樣本集,對基于EEMD和GA-LSTM方法的故障識別準確率進行驗證。
1 數據處理
1.1 集成經驗模態分解理論
集成經驗模態分解(EEMD)是為優化EMD算法中模態混疊和端點效應劣勢,而提出的一種用于分解非線性、非平穩信號的方法。
EEMD算法是通過向原始信號添加不同尺度和振幅的隨機高斯白噪聲,利用所加噪聲的頻率均勻分布的統計特性,得到多個與原始信號有相同物理意義的本征模態函數(IMF)。
在每個IMF中添加適當振幅的隨機高斯白噪聲,有助于消除離群點和擬合誤差,從而提高數據的可靠性與準確性。
1.2 EEMD算法步驟
以下為EEMD算法步驟:
1)將高斯白噪聲si(t)加入原始信號x(t)中,得到待處理信號Xi(t):
Xi(t)=x(t)+csi(t)
(1)
式中:c為白噪聲信號的幅值系數;si(t)為第i次加入的白噪聲;Xi(t)為第i次加入的白噪聲時得到的待處理信號;
2)利用EMD對待處理信號Xi(t)進行分解,得到各階IMF分量與余項Mi(t),其表達式如下:
(2)
3)對步驟1)和2)進行重復,每次都加入不同序列的隨機高斯白噪聲,其表達式如下:
(3)
4)每次分解都會得到分量與余項。為消除多次加入高斯白噪聲對真實IMF值的影響,將兩項相加求平均。采用高斯白噪聲頻譜的均值為零,計算上述各IMF均值,得到最終IMF分量為:
(4)
式中:kin為第i次EMD分解所產生的第n個IMF;n為EEMD的集成次數。
2 故障診斷網絡模型
2.1 遺傳算法
遺傳算法(GA)是一種用于尋找最佳方案的計算模型,它模擬了生物進化的過程。GA模型使用選擇、交叉和變異運算符來創建新的候選解決方案,并隨著時間的推移提高群體的適配性。GA算法廣泛用于優化問題,如工程設計、調度、機器學習等,對解決非線性和全局優化問題等具有良好的效果。
GA模型的基本原理如圖1所示。
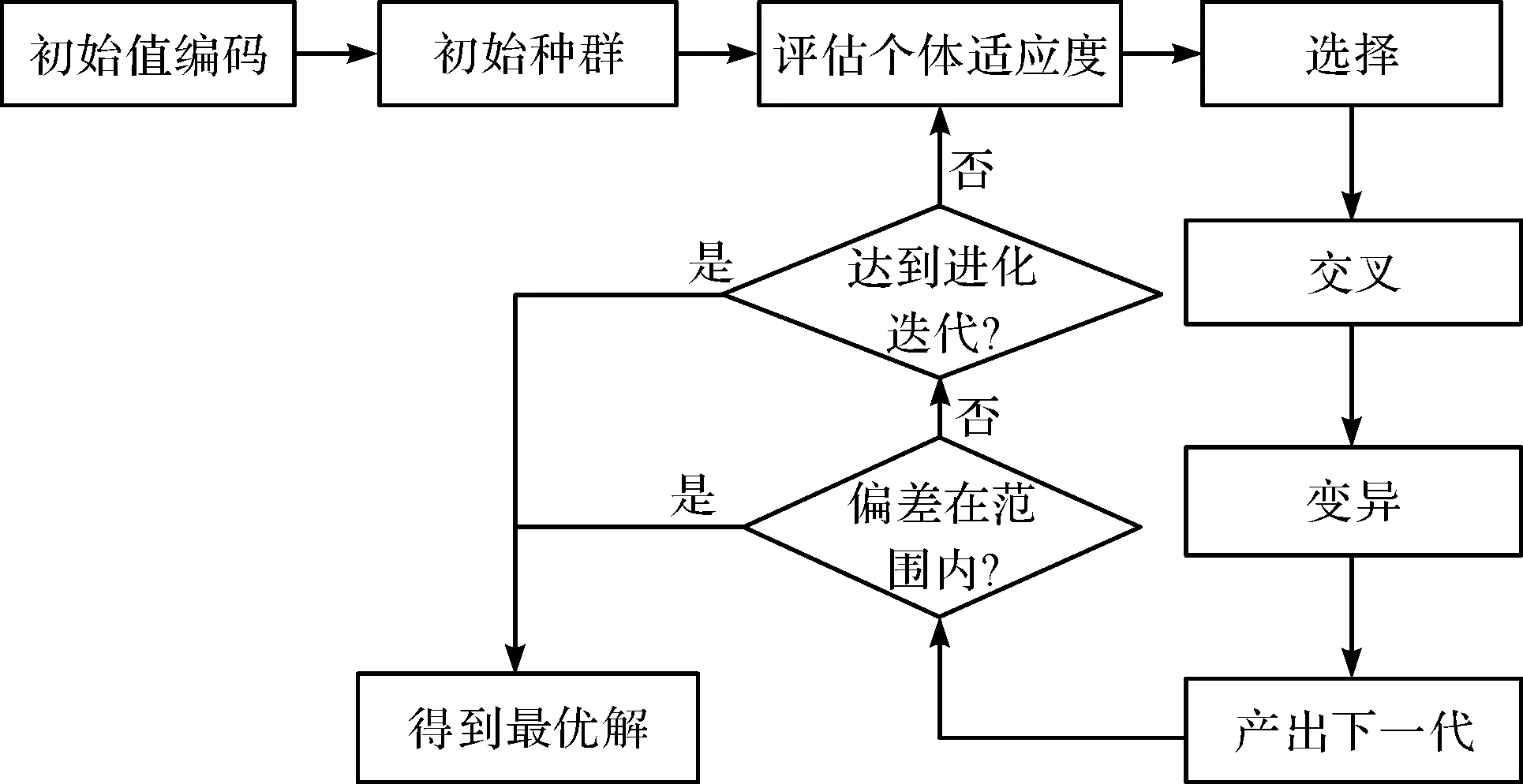
圖1 GA模型的基本原理
2.2 長短期記憶遞歸神經網絡
長短期記憶神經網絡是遞歸神經網絡(recurrent neural networks,RNN)中的一種。與RNN相比,LSTM克服了梯度消失問題,且具有更強的記憶能力,更擅長處理冗長的順序信號。LSTM引入特殊的“門”機制,通過其3個門控(遺忘門、輸入門和輸出門)學習時間序列特征[21]。
神經單元結構如圖2所示。
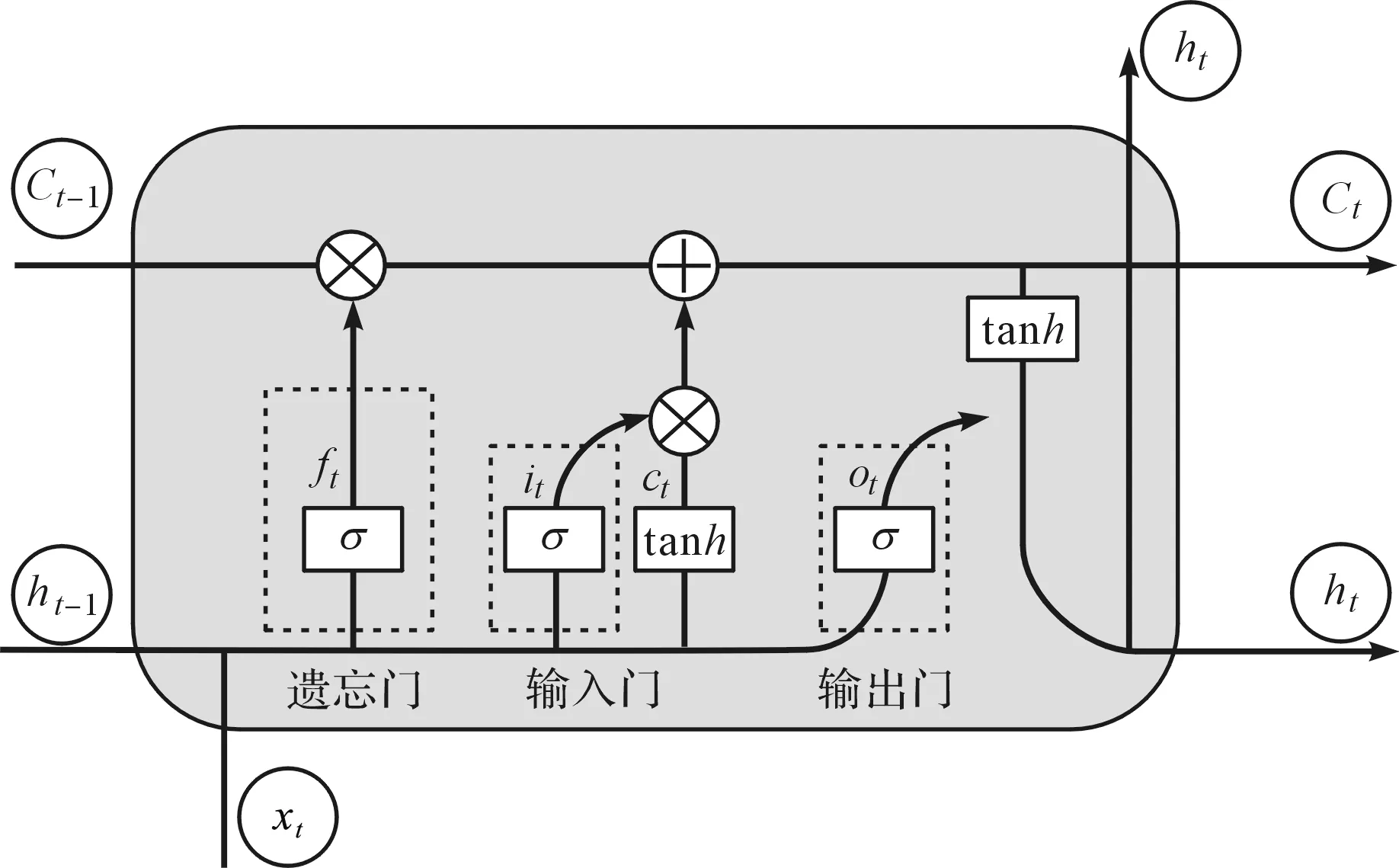
圖2 LSTM神經單元結構
LSTM的運算過程為:遺忘門ft利用當前輸入xt和最后時間步長的外部狀態ht-1,同時執行sigmoid函數,評估是否保留先前的神經元信息Ct-1。
遺忘門ft的輸出為0,表示先前神經元信息將被丟棄;當輸出為1時,表示上一時刻信息被保留。
遺忘門的表達式如下:
ft=σ(Wf·(ht-1,xt)+bf)
(5)
式中:σ為sigmoid激活函數;bf為偏置;Wf為權重;Ct-1為存儲先前記憶信息的單元狀態;ft為由遺忘門控制的遺忘程度。
輸入門負責確定必要的新信息添加到單元狀態中,用來更新。輸入門的表達式如下:
it=σ(Wi·(ht-1,xt)+bc)
(6)
(7)
(8)
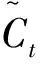
為了確定LSTM中當前神經元的輸出信息,采用了輸出門,其表達式如下:
ot=σ(Wo·(ht-1,xt)+bo)
(9)
ht=ot·tanh(Ct)
(10)
式中:ot為輸出門。
筆者使用sigmoid函數來確定當前狀態信息中應該被輸出的相關部分,然后將所得值與當前狀態信息Ct相乘,由tanh激活;隨后,所得的內部狀態信息被轉發到外部狀態,即隱藏層輸出ht。
2.3 EEMD與GA-LSTM故障診斷模型
LSTM網絡使用一個存儲單元來存儲和檢索長時間的信息,這使得網絡能夠保持順序數據的長期依賴性。但是其泛化能力差,收斂速度慢。
筆者使用GA-LSTM就是在其基礎上進行的改進,并利用GA選取最佳參數。
故障診斷模型如圖3所示。
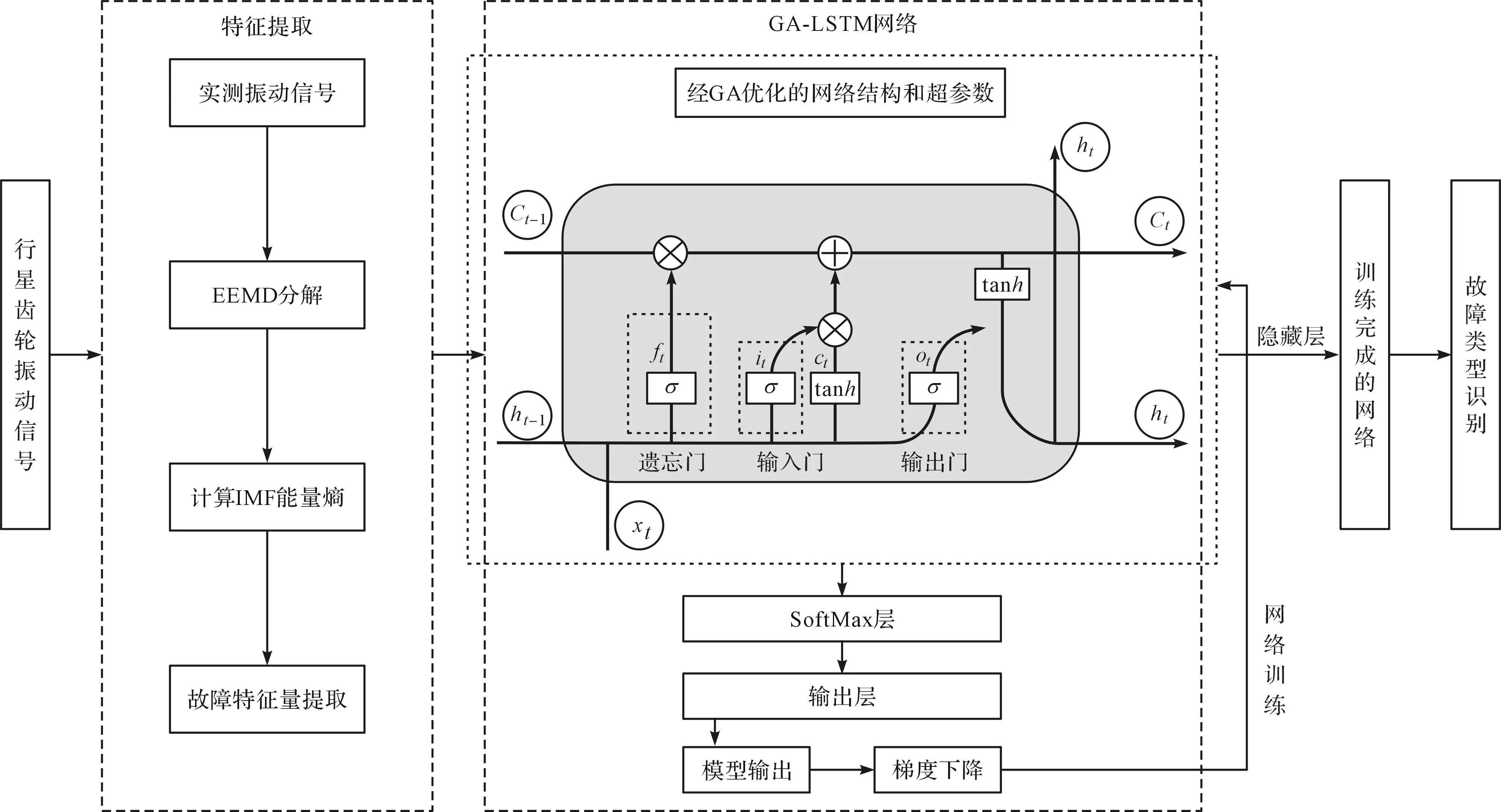
圖3 故障診斷模型
故障診斷模型步驟如下:
步驟一。采集行星齒輪的時域加速度數據,將各種狀態的振動數據分割成固定長度的序列;隨后進行預處理,用數值進行標注,將其分為訓練集和測試集,作為深度神經網絡故障診斷模型的輸入;
步驟二。在GA-LSTM層,利用遺傳算法優化權重和偏差,在訓練過程中分批接收訓練樣本,并為學習率、LSTM單元數、訓練次數等超參數選擇合適的值迭代;采用GA-LSTM層對時序數據進行計算,整合計算值后,將其輸入到SoftMax層;
步驟三。SoftMax層為每個可能的輸出類別產生一個概率分數,預測的類別是具有最高分數的類別。該層通過概率分布對故障狀態進行分類。通過比較樣本的輸出概率和實際值,得到損失率,并使用梯度下降算法不斷優化權重和偏置;
步驟四。模型訓練達到指定的迭代次數后,使用訓練好的模型對測試樣本進行預測,將預測結果與實際類別進行對比,得到模型對測試集的分類準確率。
3 實驗及結果分析
3.1 故障模擬實驗及數據集
故障模擬實驗在晉中學院故障診斷實驗室進行。
該實驗臺由驅動電機、扭矩速度傳感器和采集儀、螺旋錐齒輪箱、行星齒輪箱、底板、磁粉制動器、保護罩和控制系統組成。
實驗臺底板尺寸為1 800 mm×900 mm,齒輪箱尺寸為350 mm×250 mm。實驗內容為采集不同故障工況齒輪的振動加速度信號。
行星齒輪故障模擬實驗臺如圖4所示。

圖4 行星齒輪故障診斷實驗臺
實驗電機轉速為2 200 r/min。筆者設定采樣頻率為5 kHz。
ICP三向加速度傳感器X、Y、Z軸分別對應信號采集通道1、2、3;ICP單向加速度傳感器Z軸對應信號采集通道4,筆者將其分別設置在大小齒輪軸線處的箱蓋上,每種工況采樣時間為10 s。
為了獲得IMF分量,需要對每種狀態的信號都用EEMD進行分解。筆者將數據分為500個數據點的集合,并使用EEMD將每個集合分解為IMF分量。
在這項研究中,原始信號和前6個IMF分量被選為特征量,從而使每組數據被分解為一個特征樣本。筆者使用該方法對不同狀態的數據進行分解,共得到750組特征樣本。
故障數據集描述如表1所示。

表1 故障數據集
在試驗過程中,筆者考慮了4種不同的條件(狀態):正常狀態、齒根斷裂、齒面磨損和缺齒。
在正常和3種故障條件下,從實驗臺獲得的信號時域圖如圖5所示。
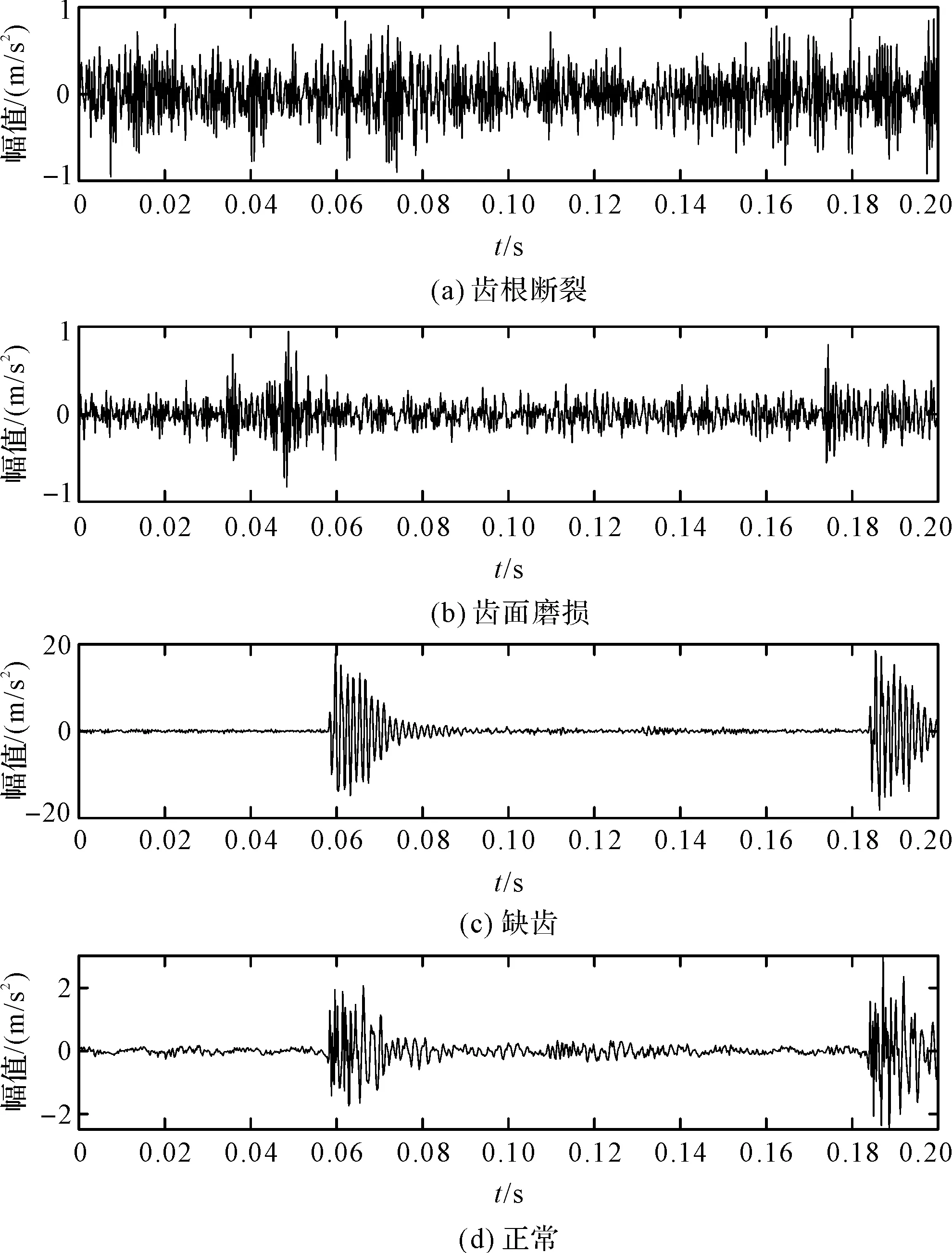
圖5 4種狀態信號的時域圖
由圖5可得:不同條件下的振動信號表現出不同的特征,其中,正常情況下表現為穩定的周期性振動信號,故障條件下的振動信號更不規則,包含脈沖狀的特征。
3.2 EEMD分解與網絡參數設置
筆者使用EEMD,對行星齒輪振動加速度進行信號分解,以獲得IMF分量,然后按頻率對IMF分量進行排序,并在其中加入標準偏差為0.1的高斯白噪聲,共得到6個IMF分量。
在不同的運行條件下,對齒輪信號進行分解,其中一種IMF分量如圖6所示。
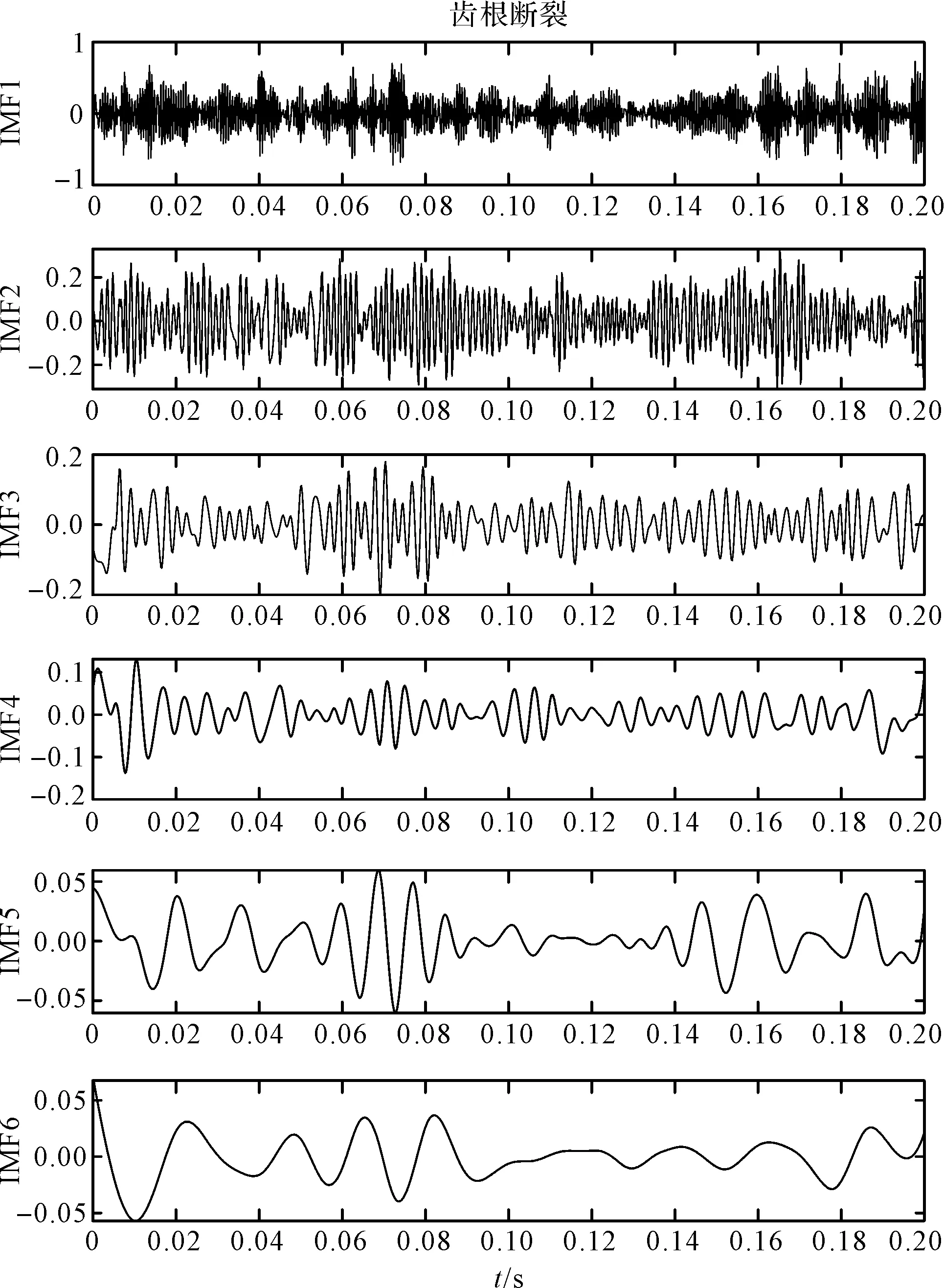
圖6 齒根斷裂信號EEMD分解圖
為了提高預測精度,筆者采用遺傳算法(GA)[22-23]對LSTM進行優化,這樣可避免人為設置超參數時存在的主觀性影響,也節省了計算資源和時間成本。
GA-LSTM網絡參數設置如表2所示。
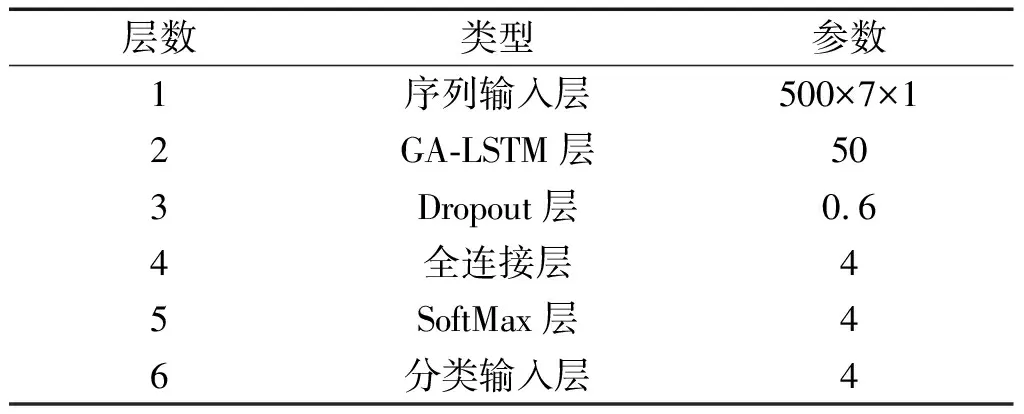
表2 網絡參數設置
筆者利用GA-LTSM網絡模型來識別最初的6個模態成分,并為其配置相應的參數。GA-LSTM模型由1個GA-LTSM層、1個SoftMax層、1個全連接層和1個分類輸出層組成。其中,為避免模型的過擬合問題,在全連接層中增加了Dropout隨機失活層,并在Dropout層中設置失活概率為0.6。
此外,還可以使用小批次設定,使模型更頻繁地更新參數,并且可以降低對內存的需求。
經GA優化的LSTM網絡的超參數如表3所示。

表3 GA-LSTM網絡模型超參數設置
循環數代表訓練次數,筆者設置為100次,每個循環后網絡都會迭代更新。模型的運行環境為MATLAB。
3.3 實驗結果分析
在該實驗中,筆者隨機選取90%的數據作為訓練樣本,并使用GA-LSTM網絡對樣本進行訓練。
損失隨迭代次數變化的情況如圖7所示。
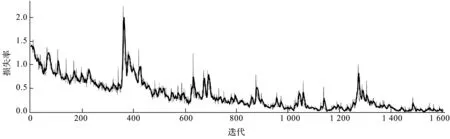
圖7 迭代次數與模型的訓練損失率的關系
從圖7中可以看出:該網絡的損失率低于2%,證明了該網絡具有良好的穩定性。
筆者使用剩余10%的數據進行測試。模型訓練準確率曲線如圖8所示。
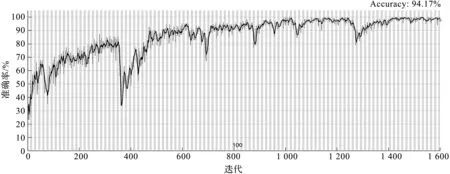
圖8 模型訓練準確率曲線
由圖8可知:模型經過測試后,得到了該模型的精度為94.17%;同時,在迭代計算過程中,訓練曲線會產生一定的波動,表明該模型在進一步迭代中可以達到穩定的預測效果。
筆者利用混淆矩陣展示模型分類的評估性能,如圖9所示。
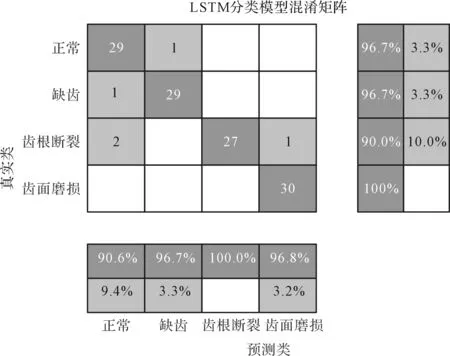
圖9 測試結果混淆矩陣
由圖9可以發現:模型能比較準確地識別出行星齒輪的缺齒、正常和齒面磨損情況,但是對行星齒輪齒根斷裂情況的識別率最低,為90.0%,這表明模型還存在齒根斷裂被誤判的問題,導致結果偏差增加(其原因是在特征判斷上,與其他故障類型相比,齒根斷裂容易被誤判為正常情況)。
因此,筆者還需要進一步優化模型,以提高對齒根斷裂的識別率。
綜上所述,該網絡在行星齒輪故障識別方面表現良好,是一個可靠的分類工具。
3.4 對比分析
3.4.1 必要性驗證
未經EEMD處理以及經過EEMD處理的網絡,在迭代測試精度方面的情況如圖10所示。
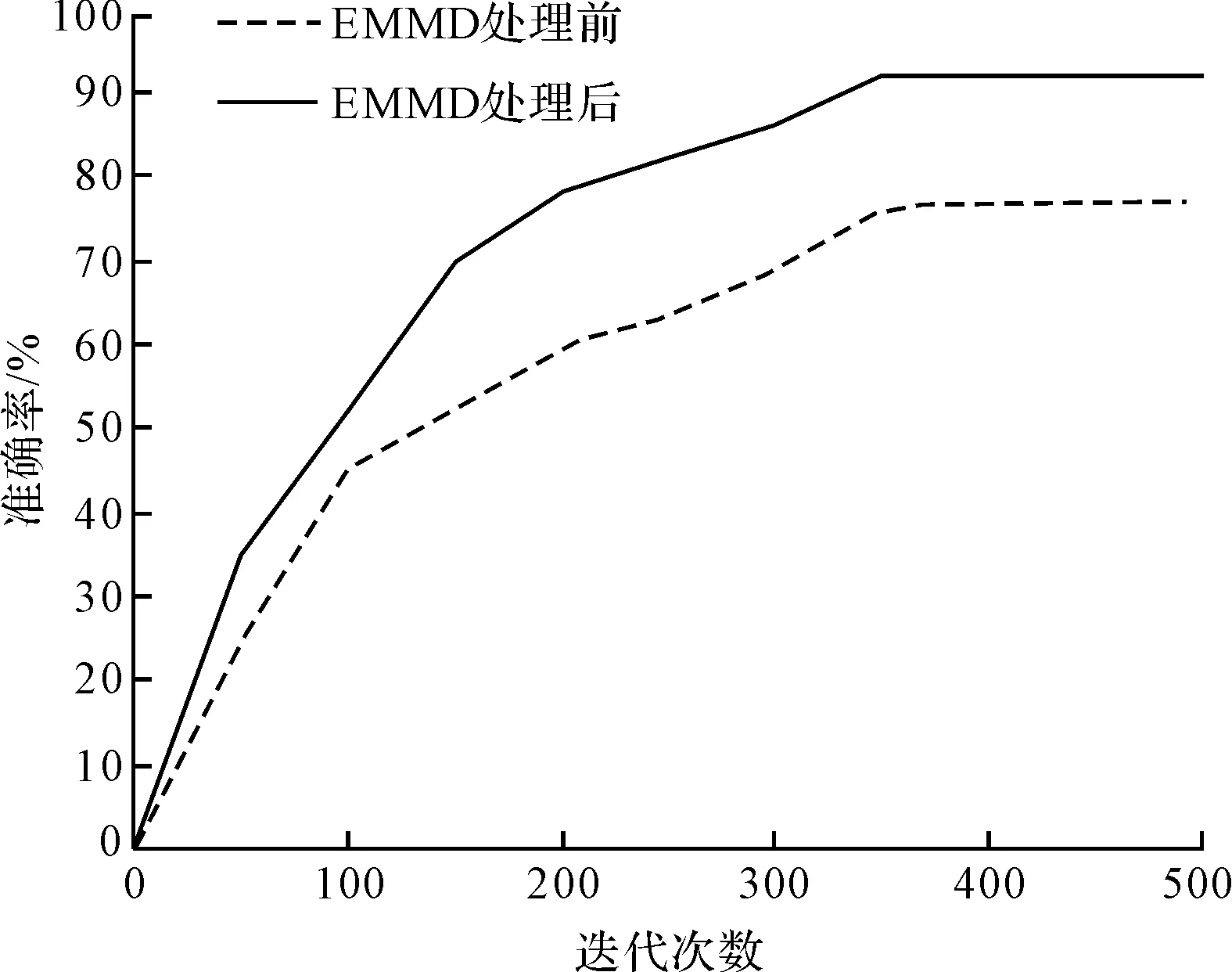
圖10 網絡精度隨EEMD處理前后迭代次數的變化
由圖10可以得知:未進行EEMD處理的網絡表現出相對較差的穩定性,其精度僅能達到78%;經過使用EEMD處理后的網絡,可以實現94%的準確率,同時穩定性和精度也得到了顯著提升。
這表明,使用EEMD方法處理數據有利于改善網絡的穩定性和精度,同時也說明LSTM網絡更適合用于處理時序信號。
由于該實驗是模擬的,而在實際工作條件下,行星齒輪可能會遇到更多的噪聲干擾,這會大大削弱故障信號的特征,使得其特征提取更具有挑戰性。
為了進一步模擬行星齒輪的實際工作情況,筆者在其原始振動信號中加入了噪聲,并對這種添加噪聲的影響進行了分析,結果如圖11所示。
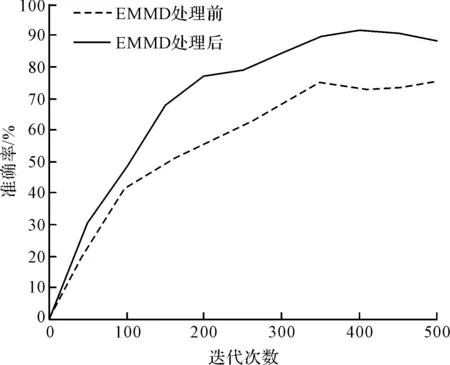
圖11 添加噪聲后EEMD處理對模型精度的影響
由圖11可以看出:如果沒有對添加噪聲的信號進行EEMD降噪處理,其分類結果會變差;反之,添加噪聲后,對EEMD和GA-LSTM網絡而言,其分類精度仍然保持在相對較高的水準上。這說明,在實際應用中,EEMD方法能有效地減少噪聲的干擾,提高行星齒輪的故障診斷精度;
當加入噪聲后,該模型的準確度達到了90.0%;而當使用沒有經EEMD分解的信號時,其準確度只有75.3%。這證明,使用EEMD算法的信號分解有效地減輕了噪聲的影響,并提高了模型的準確性;
此外,與直接將噪聲信號輸入模型相比,使用分解后的信號,其在精確度上顯著提高了15%。因此,可以推斷:EEMD處理方法及其結合LSTM網絡的方法可能會在時序信號處理領域有更為廣闊的應用。
3.4.2 優越性驗證
在初始迭代測試階段中,2個網絡都表現出了快速收斂狀態,GA-LSTM和LSTM網絡的準確性對比如圖12所示。
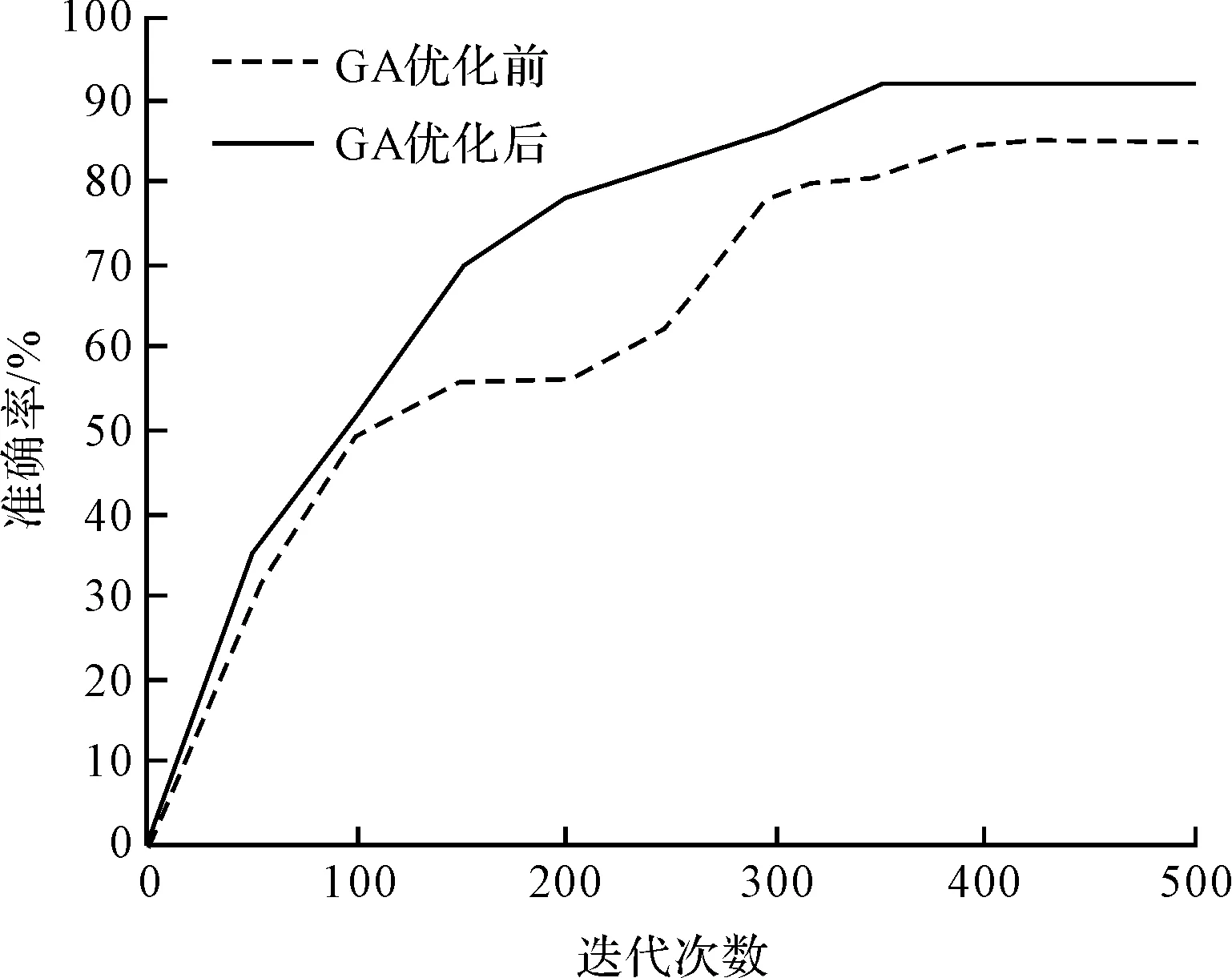
圖12 迭代次數與不同網絡模型準確性之間的關系
由圖12可知:實驗結果表明,與沒有優化的模型相比,用GA算法優化的LSTM網絡的準確性從85%提升到94%,預測的準確度提高了9%,其原因是兩種網絡都采用類似的訓練方式,即單向的往前訓練方式;
兩者相比而言,GA-LSTM網絡更加平滑,這是因為GA優化是通過優化LSTM層參數去除其人為設定的隨意性,避免了網格尋優方式耗費大量時間和計算資源。隨著迭代次數的增加,2個網絡的精度逐漸提高。
值得注意的是,到達后期迭代階段時,GA-LSTM網絡比未經過優化的LSTM網絡獲得了更好的精度。這證明了GA-LSTM網絡的優化策略確實有效地提升了網絡性能。
4 結束語
筆者將EEMD與基于GA-LSTM的神經網絡相結合,提出了一種新的行星齒輪故障診斷方法,并利用故障模擬實驗平臺,對4種不同狀態的行星齒輪數據集進行了測試,對該方法的有效性與泛化性進行了驗證。
研究結論如下:
1)相比于傳統的故障診斷技術,EEMD方法能有效地將非線性和非平穩信號分解為多個本征模式函數分量,IMF分量可以作為進一步處理和分析的特征,從而提高故障診斷的準確性和可靠性;
2)使用遺傳算法來優化LSTM網絡模型,可以顯著提高網絡的泛化能力,并且在加快訓練過程和降低過擬合的風險方面也具有優勢。實驗結果顯示,相比于傳統LSTM算法,GA-LSTM算法的準確率更高(達到了94%),而傳統LSTM算法僅能達到85%的準確率;
3)GA-LSTM模型的總體故障診斷準確率達到了94.17%。在人為加入噪聲信號后,與未經EEMD分解的模型相比,該模型在精確度上提升了15%,表明該模型對噪聲信號具有較強的魯棒性,具備良好的抗噪聲能力。
綜上所述,筆者所提出的故障診斷方法具有更高的識別率和更強的魯棒性,該方法可為行星齒輪故障診斷提供良好的應用前景。
在未來的研究中,筆者旨在將上述行星齒輪故障診斷方法擴展到更具挑戰性的場景中,如強噪聲干擾和可變工況,以進一步優化并提高該模型的抗噪聲能力和泛化能力,使其更加適用于不同的環境和場景。

