基于單錨點UWB的室內定位技術

石豪東，付 銘，夏雨嘯，劉銀華

（青島大學 自動化學院，青島 266071）

隨著經濟發展不斷地提高，民生科技的需求增加，大量服務于人們生活的機器人隨之出現，例如掃地機器人、預警機器人等。

這些產品的出現意味著人們對定位技術精度和可靠性的要求不斷提高，各種新型定位技術和算法也應運而生。市場上的室內定位技術層出不窮，WiFi、紅外定位、藍牙等技術已經大量應用于室內定位，但對于復雜環境下尤其是非視距環境（none line of sight，NLOS）下，WiFi 和紅外定位技術會因信號的衰減或者是障礙物的遮擋而導致定位產生很大的誤差。在環境復雜的室內場所GPS、北斗等衛星定位技術由于衛星信號較弱，無法穿透屋頂、隧道等障礙，這導致此類定位技術無法用于室內環境[1]。而基于UWB 的定位跟蹤技術具有定位精度高、魯棒性好、適應性強等優勢，已經成為當前定位技術中的研究熱點。

UWB 定位系統是基于超寬帶通信的，超寬帶通信因為其高頻特性，能夠較容易地獲取時間信息，基于時間特征的定位技術能夠獲取到更高精度的定位結果[2]。在文獻[3]中描述了一個精度可以達到4 cm 的超寬帶定位系統與之比較的是GPS 定位系統，實驗結果表明超寬帶技術的效果非常優越。UWB雖然可以實現高精度的定位，但是需要多錨點的距離信息共同計算目標位置，如果減少UWB 的錨點數量，就會導致位置信息的丟失，無法準確定位。

慣性傳感單元（inertial measurement units，IMU）集成了加速度計、角速度計和磁力計3 種傳感器，得益于其成本較低、體積較小以及精度較高，其在姿態識別、導航定位等研究領域中被廣泛使用。但由于其具有零偏以及隨意游走的誤差特性，所以單獨使用IMU 時誤差較大。

UWB 無線信號雖然可以提供高精度的距離測量數據，但由于受到障礙物和信號衰減的影響，它在室內或者復雜環境下的定位精度受到限制。而IMU 慣性傳感器可以提供相對運動狀態的信息[4]，但隨著時間的推移，它的誤差會不斷累積，從而導致定位精度下降。為了克服UWB 和IMU 各自的限制，研究者們提出了許多融合算法和濾波算法[5]，卡爾曼濾波算法是一種常用的濾波算法，它可以通過處理UWB 和IMU 數據，得到更加準確和可靠的目標定位跟蹤結果，但在非線性系統中卡爾曼濾波技術的穩定性和魯棒性有待提高，考慮通過擴展卡爾曼濾波（EKF）將UWB 和IMU 所提供的位置信息進行融合，通過融合這兩種數據來提高定位精度和魯棒性。

因此，本文旨在探討基于UWB 和IMU 的定位技術，并利用EKF 算法進行數據處理，以提高定位精度和魯棒性。在系統設計和實驗過程中，將對UWB和IMU 數據進行預處理，構建數學模型來描述目標運動狀態，利用EKF 算法進行數據融合和濾波處理，以實現高精度和魯棒性的目標定位跟蹤。

1 定位系統架構

1.1 UWB 系統

UWB 通過窄脈沖實現高帶寬信號傳輸，傳輸速率高，不容易被其他信號影響，從而能實現高精度的目標定位。其測距原理為檢測多個錨點之間的信號傳輸時間（TOF）和信號到達時間（TOA）計算兩個節點之間的信號的接收與發送的時間，記錄響應時間差通過式（1）即可獲得信號的平均飛行時間ttof：

根據式（2），即可完成測距，其中c 為光速：

如圖1 所示，計算出2 個節點之間的距離后，根據文獻[6]中的描述，超寬帶定位系統在預設位置上部署固定節點的情況下，可以通過最小二乘法的三邊定位法，如圖2 所示，計算錨點與固定節點的距離從而獲得目標的位置信息。

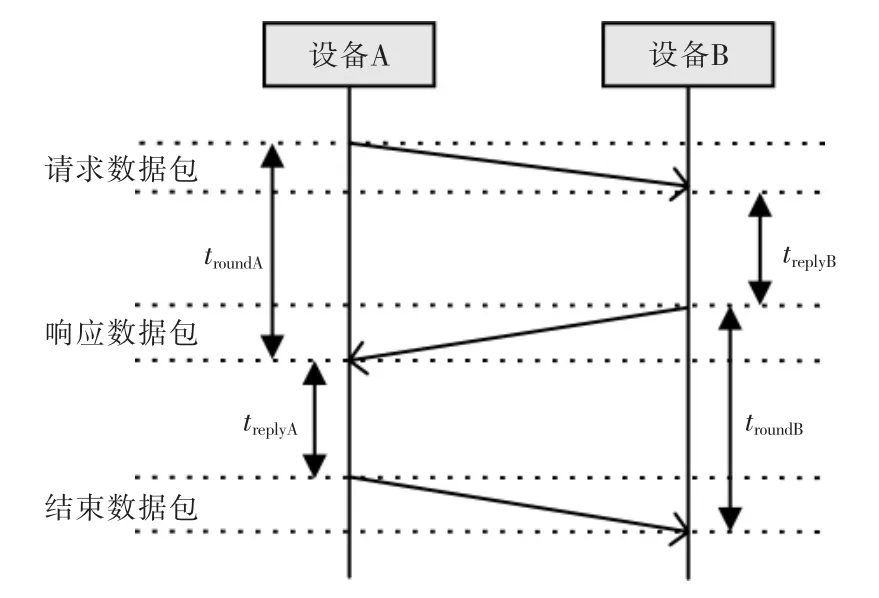
圖1 UWB 測距原理圖Fig.1 UWB ranging schematic diagram

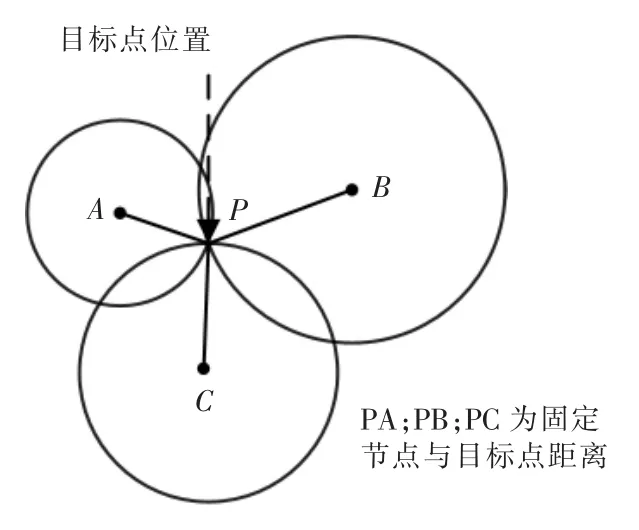
圖2 三邊定位原理圖Fig.2 Three-sided positioning schematic diagram

1.2 慣性導航系統

IMU 定位系統需要設置載體坐標系與導航坐標系，所述的載體坐標系（b 系）Y 軸指向前進方向，X 軸水平向右，Z 軸垂直向下；導航坐標系（n 系）采用北東地坐標系；姿態角由載體坐標系到導航坐標系之間的相對角位置關系來表示，用歐拉角來對目標姿態進行描述，歐拉角包括俯仰角、橫滾角和偏航角，俯仰角是坐標系沿Y 軸旋轉的角度，旋轉范圍為-90°～+90°；橫滾角是坐標系繞X 軸旋轉的角度，旋轉范圍為-180°～+180°，偏航角是坐標系繞Z軸旋轉的角度，旋轉范圍為0°～360°。

兩個坐標系之間的相互轉換可以用姿態矩陣來表示：

上述矩陣可記為

則通過上述2 個矩陣的關系可以獲得3 個姿態角（橫滾角、俯仰角、偏航角）的計算公式分別為

1.3 單錨點的UWB 設計

配置多個錨點的UWB 定位技術難點在于定位目標時，目標機器人為節點，所構架的多個錨點如果與節點時鐘不同步就無法使用上述的三邊定位法計算目標位置。而且需要在預設的場地提前安裝校準錨點，需要大量的前期人工工作。如圖3 所示，現實生活中多是隨機化的場景，所以提前構建場地安裝錨點是很難實現的。

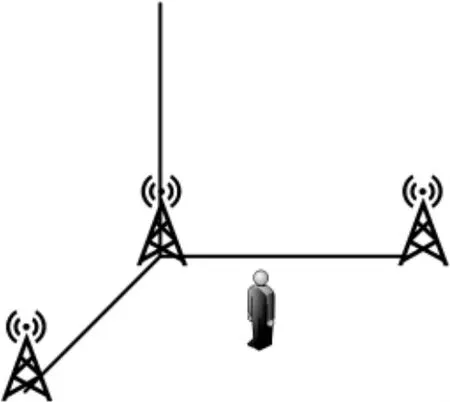
圖3 UWB 錨點設置Fig.3 UWB anchor setting diagram

單錨點技術實現目標定位，不再需要繁雜的設備安裝，而且有效地降低了技術成本。本方案雖然簡化了系統構建的復雜度但還存在一個問題，如果只保留一個UWB 錨點，即只通過單一信號源獲得的距離信息完成精確的目標定位是遠遠不夠的。所以在只有一個UWB 錨點的情況下，需要加入其他傳感器來獲得目標的位置信息，采用從低成本的IMU傳感器中觀測目標在3 個軸向上的加速度和角速度，從而獲得目標的姿態信息，結合UWB 提供的位置信息經過擴展卡爾曼濾波算法進行數據融合從而獲得精確的位置估計。

2 系統數學模型

在本節中闡述了如何實現兩種傳感器數據的信息融合，以及模型的構建。基于數學運動模型進行多傳感器融合，根據現實生活中機器人的運動狀態通常是在勻速狀態下進行的，所以采用二階的CTRV模型作為系統的狀態模型。該模型的運動狀態為位置、速度、加速度和方向。CTRV 模型假設對象以恒定的角速度進行勻速運動，加速度為系統的過程噪聲，通過加速度噪聲對系統進行誤差補償，減少震蕩，提高系統的精度與穩定性，增強系統的魯棒性，其中估計器一般使用卡爾曼估計器計算出目標位置，如式（8）和式（9）所示：

式中：xk為狀態向量，描述了機器人在坐標系中的位置和速度信息；uk為輸入向量機器人的加速度和角速度信息；zk為觀測向量，包含了機器人的位置和方向信息；fk為狀態轉移矩陣；Bk為控制輸入矩陣；hx為觀察矩陣；其中wk（0～Q）和vk分別表示過程噪聲和傳感器噪聲描述了狀態轉移過程中的不確定性，它們都是符合高斯分布的白噪聲。

由于機器人的運動過程并不是一個連續的線性的過程，無法用傳統的卡爾曼濾波器進行位置信息估計。

對于非線性系統可以將機器人的運動和對其測量過程作為一個擴展卡爾曼濾波問題來進行建模，對系統函數進行泰勒級數展開從而把系統線性化，然后再使用卡爾曼估計器獲取系統位置信息。基于傳統的卡爾曼濾波系統線性化獲得的擴展卡爾曼濾波，如式（10）和式（11）所示：

擴展卡爾曼濾波分為預測和更新2 個階段，如圖4 所示。預測階段的控制輸入由IMU 中的陀螺儀、加速度計和磁力計提供，在更新階段使用的觀測信息是UWB 模塊測量的距離信息和IMU 測量的偏航角。

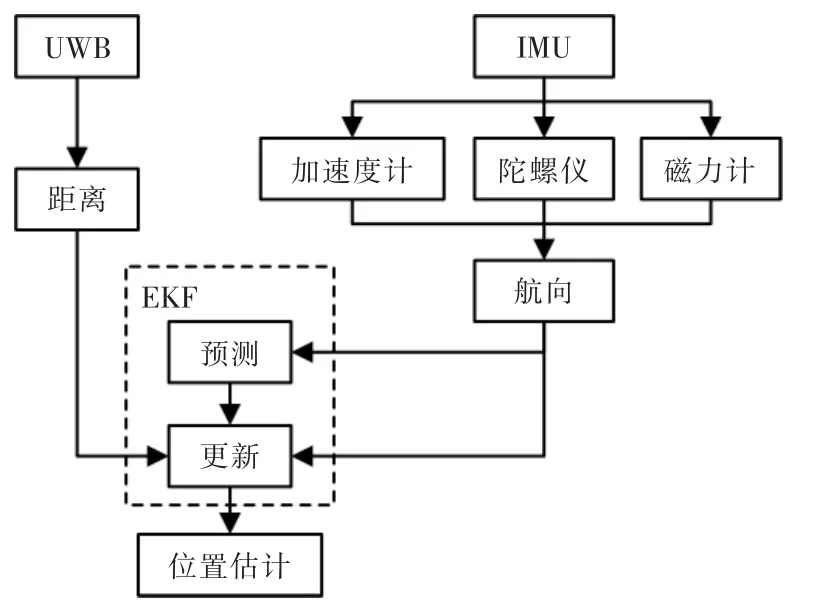
圖4 系統估計框架Fig.4 System estimation framework

2.1 位置信息的估計

本文需要構建CTRV 模型來描述目標的運動狀態。CTRV 模型是一種廣泛應用于目標定位領域的模型，可以描述目標在三維空間中的位置、速度和加速度等狀態。在本系統中，以二維平面展開描述，且其運動狀態服從恒定加速度模型。

機器人的狀態向量X=[PxPyvθ]T，其中x 和y 分別表示機器人的橫縱坐標；v 為線速度；θ 為偏航角為角速度。

式中：Px，Py分別為機器人在x 和y 方向的位置信息，系統狀態方程描述了目標在時間t 時刻的狀態，包括位置、速度和加速度，由于加速目標勻速運動所以加速度a 為0，θ¨角加速度為0，即狀態方程XK+1可表示為

式中：Δt 為采樣時間；θt為t 時刻的角度。在本系統中，將UWB 和IMU 數據進行融合，以提高定位精度和魯棒性。因此，系統的狀態方程是由IMU 傳感器數據和系統狀態向量組成的，即在EKF 的預測階段通過狀態轉移矩陣fx來描述目標的運動狀態演化過程。使用IMU 模塊通過陀螺儀、加速度計、磁力計計算物體的加速度和角速度，然后將其輸入到預測模型。由于狀態轉移函數是非線性的，因此需要對其進行線性化。具體而言，在每個采樣時間將狀態向量作為一個局部線性近似點，并使用其一階導數構建一個線性模型，這個模型通常被稱為擴展卡爾曼濾波中的雅可比矩陣。狀態轉移函數的雅可比矩陣式可以通過求解矩陣的偏導數計算得到：

2.2 誤差分析

本文把UWB 測量的距離和IMU 測量的角度θ作為觀測向量Hx，系統的觀測方程為hx，即：

UWB 模塊通過式（17），測量物體與錨點之間的距離d 為

在EKF 的更新階段，通過計算卡爾曼增益來融合IMU 和UWB 的觀測值，得到一個最終的估計值。卡爾曼增益是一個重要的參數，用于確定如何將當前的觀測信息與先前的估計值進行融合。所以卡爾曼增益的計算為系統估計的關鍵。

式中：Kk為系統的卡爾曼增益；Jh為觀測矩陣的雅可比矩陣；Pk為更新誤差的協方差矩陣；Pkˉ為先驗誤差的協方差矩陣；Q 為誤差的協方差矩陣，可由式（21）計算獲得：

將獲得的測量值作為觀測向量輸入到擴展卡爾曼濾波器中，以獲得更加準確的位置和速度估計值。

本系統的誤差主要來自于加速度，雖然假設系統加速度a 和角加速度θ¨為常數，但在實際的運動中，速度的改變是無法忽略的，所以過程噪聲會影響系統的準確性，需要在更新階段對系統進行誤差補償可以更加符合真實軌跡，wk是一個零均值的高斯白噪聲向量，即：

3 實驗與分析

3.1 實驗設計

為了驗證該算法的可行性與準確性，在自主研發的室內機器人，如圖5 所示，搭載了Decawave 公司生產的DWM1000 芯片和自主研發的9 軸IMU，傳輸頻率為50 Hz/s。DWM1000 芯片負責接收機器人與錨點間的距離信息；9 軸IMU 負責提供加速度信息用于系統預測與更新，通過WiFi 將兩個傳感器測得的位置信息傳輸到PC 端。給機器人設置一段固定路徑，其原點為UWB 錨點所在位置，獲取位置信息驗證跟蹤路徑的準確性。

圖5 實驗小車Fig.5 Experimental car

3.2 實驗分析

分別設置2 種軌跡，分析該算法的可行性，記錄實驗數據如表1 所示。

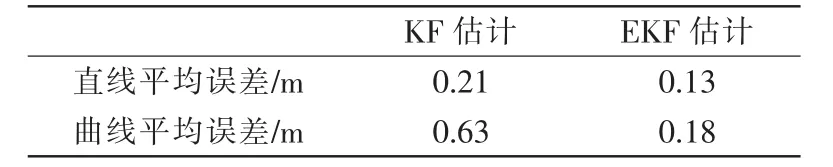
表1 跟蹤誤差數據分析Tab.1 Tracking error data analysis

首先對直線運動進行誤差分析，如圖6 和圖7所示，在卡爾曼濾波的情況下，系統的平均誤差大約在0.21 m，其中波動最大處超過了0.30 m，而經過擴展卡爾曼濾波處理下的跟蹤軌跡的平均誤差只有0.13 m，而且沒有大幅度的波動。

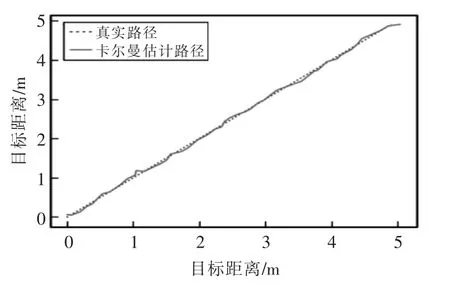
圖6 卡爾曼濾波估計直線路徑Fig.6 KF estimates linear paths

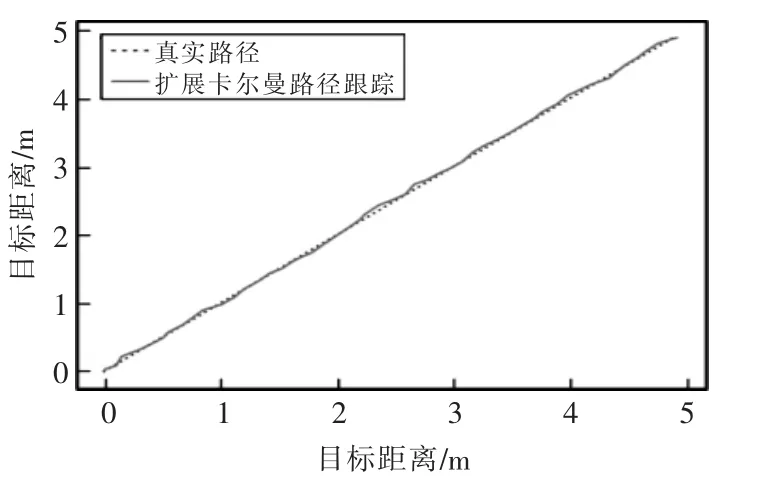
圖7 擴展卡爾曼濾波估計直線路徑Fig.7 EKF estimates linear paths

如圖8 和圖9 所示，在曲線軌跡下運動的小車明顯出現了更大的誤差，尤其是通過卡爾曼濾波器估計出的位置有很大的偏差，平均誤差甚至超過了0.5 m，而通過擴展卡爾曼濾波器所估計出的位置平均誤差只有0.18 m。雖然在速度有大幅度波動時系統產生了較大的誤差，但是系統可以快速的恢復穩定，具有良好的魯棒性。

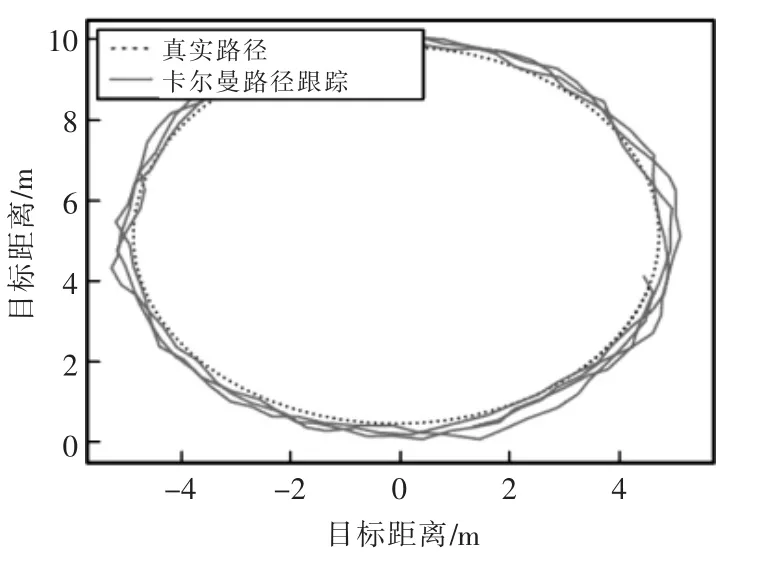
圖8 卡爾曼濾波估計曲線路徑Fig.8 KF estimates curve path

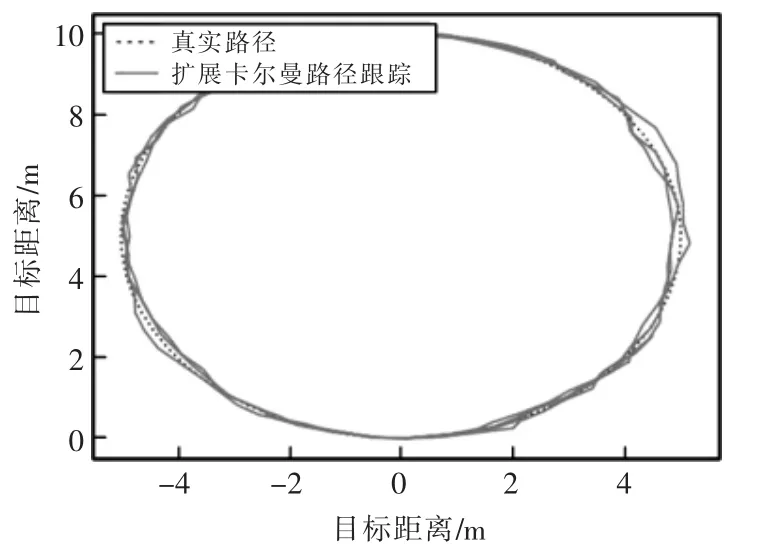
圖9 擴展卡爾曼濾波估計曲線路徑Fig.9 EKF estimates curve path

4 結語

本文設計了一種單錨點的UWB 目標定位算法，通過擴展卡爾曼濾波實現UWB 和IMU 的數據融合，提高定位系統的精度。經過實驗，單錨點的UWB 在IMU 的配合下可以大幅提高定位的精確性，驗證了本方法的可行性。實驗也表明了在速度發生突變時，系統誤差增大，跟蹤軌跡發生了漂移，影響了系統的準確性，這也是此方法存在的不足，后續的研究重點考慮解決速度發生突變時系統產生的漂移所帶來的誤差影響，提高系統的魯棒性。