指數函數與對數函數的“有緣相聚”
■向光榮
指數函數與對數函數都是基本初等函數,它們常常在一個題目中“相聚”。
一、“相聚”在求值問題中

評注:分段函數的求值問題,應注意各段函數中自變量的取值范圍。
二、“相聚”在定義域問題中
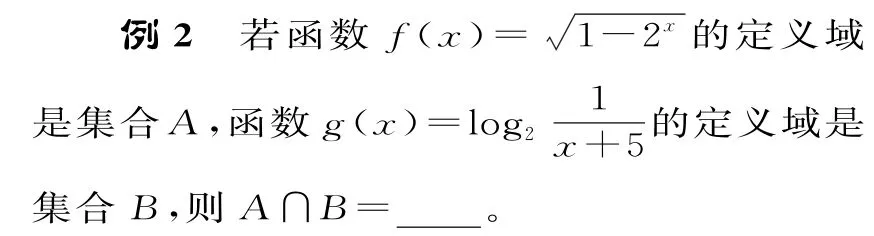

故A∩B=(-5,0]。
評注:若二次根式有意義,則被開放數應為非負數;若對數有意義,則真數應大于0。
三、“相聚”在值域問題中
例3已知函數f(x)=1+log2x,g(x)=2x。 若F(x)=f[g(x)]·g[f(x)],則F(x)在x∈[1,4]上的值域為____。

因為f(x)=1+log2x,g(x)=2x,所以函數F(x)=f[g(x)]·g[f(x)]= (1 + log22x)·21+log2x=2(1+x)·2log2x=2x(1+x)=2x2+
由二次函數的性質可知,當x∈[1,4]時,F(x)為增函數,所以F(x)的最大值為F(4)=40,F(x)的最小值為F(1)=4,所以F(x)在x∈[1,4]上的值域為[4,40]。
評注:求二次函數在區間[a,b]上的值域,應注意二次函數在區間[a,b]上的單調性。
四、“相聚”在邏輯問題中
例4“lnx>lny”是的( )。
A.充分不必要條件
B.必要不充分條件
C.充要條件
D.既不充分也不必要條件

評注:若p?q,且q?/p,則p是q的充分不必要條件。
五、“相聚”在比較大小問題中
例5已知f(x)是偶函數,且當x∈(0,+∞)時,函數f(x)=ex+x3+x,若a=,則a,b,c的大小關系為____。(用“<”連接)

因為當x∈(0,+∞)時,f(x)=ex+x3+x,所以函數f(x)在(0,+∞)上單調遞增。
因為f(x)是偶函數,所以a=f(-log35)=f(log35),b=f(-log53)=f(log53)。
又0 評注:對數值比較大小的四種方法:化同底后利用函數的單調性;作差或作商法;借助中間量(0或1);化同真數后利用圖像比較。 例6已知函數f(x)是定義在[1,+∞)上的單調函數,且對任意x∈[1,+∞),均有f[f(x)-log2x]=1。若關于x的方程4f(x)-a·2f(x)+1=0有解,則實數a的取值范圍為( )。 令f(x)-log2x=t,則f(x)=log2x+t,所以函數f(t)=log2t+t。 因為f(x)是定義在[1,+∞)上的單調函數,且對任意x∈[1,+∞),均有f[f(x)-log2x]=1,所以f(t)是定義在[1,+∞)上的單調函數,且f(1)=1,所以t=1,所以f(x)=log2x+1,且f(x)≥f(1)=1。 令2f(x)=m,則m∈[2,+∞)。 評注:函數f(x)的值域為[m,n],若方程a=f(x)有解,則m≤a≤n。 例7已知函數是R 上的奇函數,則實數a=____。 評注:若f(x)是奇函數,則f(-x)+f(x)=0恒成立。六、“相聚”在方程問題中
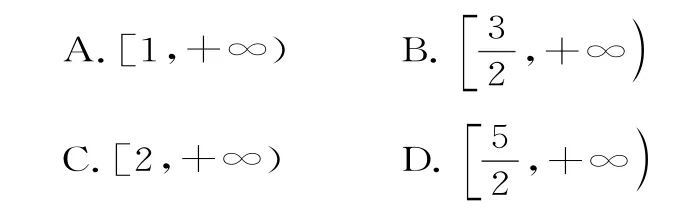



七、“相聚”在奇偶性問題中




