指數函數與對數函數考點直擊
■易麗華
指數冪的運算與對數的運算這兩個知識點,既是學習和研究指數函數、對數函數的基礎,也是高考的必考知識之一,同學們在學習中應給予足夠的重視。指數函數、對數函數是重要的基本初等函數,它們的圖像與性質是高考考查的重點。因為指數函數與對數函數的圖像與性質都與底數的取值有密切的聯系,所以在底數的取值不確定時,一定要注意進行分類討論。
考點一:指數函數、對數函數的定義域與值域問題

求指數函數與對數函數的定義域主要通過構建不等式(組)來求解,有時解不等式(組)時需要借助于指數函數與對數函數的單調性。涉及指數函數與對數函數的值域問題有兩個類型,一是形如y=af(x)和y=logaf(x)的函數,先要求出f(x)的值域,再利用指數函數與對數函數的單調性求解,二是形如y=f(ax)和y=f(logax)的函數,要根據ax和logax的取值范圍,利用函數y=f(x)的性質求解。
考點二:指數函數、對數函數的圖像與性質問題
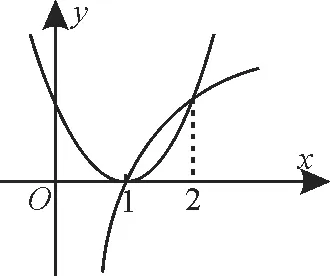
例2當時,4x 解答這類問題要熟練掌握指數函數、對數函數,以及冪函數的圖像與性質。對于方程與不等式問題,可利用函數的單調性進行轉化,也可利用數形結合法解決,對于含參數的問題,要進行分類討論,同時還要注意參數本身的取值范圍,以免出現增根。 例3(1)若a=20.2,b=log43.2,c=log20.5,則( )。 A.a>b>cB.b>a>c C.c>a>bD.b>c>a A.a C.c 解:(1)由a=20.2>1>b=log43.2>0>c=log20.5,可得a>b>c。應選A。 比較大小的常用方法有單調性法,圖像法,中間搭橋法,作差法、作商法等。當需要比較大小的兩個實數均是指數冪或對數式時,可將其看成某個指數函數、對數函數或冪函數的函數值,然后利用該函數的單調性比較大小。 例4若不等式(x-1)2 解:設函數f1(x)=(x-1)2,f2(x)=logax,要使當x∈(1,2)時,不等式(x-1)2 當0 圖1 當x∈(1,2)時,要使f1(x)=(x-1)2的圖像在f2(x)=logax的圖像下方,只需滿足f1(2)≤f2(2),即(2-1)2≤loga2,所以loga2≥1,所以a≤2,所以1 解決對數函數的參數取值范圍問題應注意的三個方面:對數函數圖像的運用,也就是我們常說的數形結合思想的應用;分類討論思想的運用,如果對數函數的底數是參數a,一般要分a>1和0 例52022年6月5日神舟十四號載人飛船在長征二號F遙十四運載火箭的托舉下點火升空,成功進入預定軌道。我國在航天領域取得的巨大成就,得益于我國先進的運載火箭技術。根據火箭理想速度公式v=v0·,可以計算理想狀態下火箭的最大速度v(單位:m/s),其中v0(單位:m/s)是噴流相對速度,m(單位:kg)是火箭(除推進劑外)的質量,M(單位:kg)是推進劑與火箭質量的總和,稱為總質比。已知A型火箭噴流相對速度為800m/s,根據以上信息,回答下列問題。 (1)當總質比為50時,求A型火箭的最大速度。 (2)若經過材料更新和技術改進后,A型火箭的噴流相對速度提高到原來的2 倍,總質比變為原來的,若要使火箭的最大速度至少增加800m/s,求在材料更新和技術改進前總質比的最小值。(所有結果保留整數,參考數據:ln2≈0.693,ln5≈1.609,e≈2.718) 解:(1)當總質比為50時,A型火箭的最大速度v=800ln50=800(2ln5+ln2)≈800(2×1.609+0.693)=3 128.8 ≈3129(m/s)。 故在材料更新和技術改進前總質比的最小值為68。 本題以實際生活為背景,考查了對數運算與解對數不等式問題。在閱讀理解題意的基礎上,方可尋找解題的突破點,體現了運算求解能力,以及分析問題、探究問題的數學素養。


考點三:比較大小問題
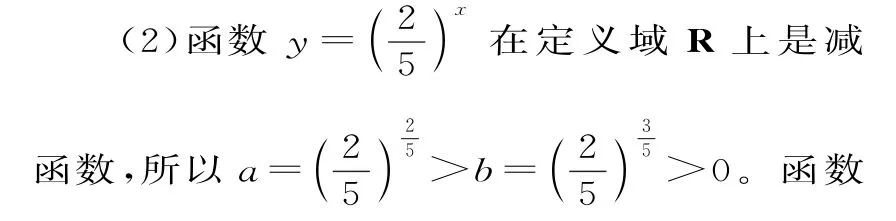


考點四:指數函數、對數函數的性質應用問題

考點五:指數函數、對數函數的實際應用問題



