嵌套函數的零點問題
■盛文斌
嵌套函數作為復合函數的一種形式,在高考命題中經常出現。嵌套函數分同一個函數間的嵌套與不同函數間的嵌套,利用復合函數的形式加以合理嵌套,巧妙融入零點及其應用問題,成為高考中的一類比較綜合的創新應用問題,倍受大家的關注。
一、整體思維,分類討論
對于一些相對簡單的嵌套函數的零點問題,可以將其內層函數加以整體化處理,借助整體思維進行合理轉化,由內到外通過分類討論,達到解決問題的目的。
例 1 已 知 函 數f(x) =則函數y=f[f(x)]+1 的所有零點構成的集合為____。
分析:根據題設條件,化嵌套函數的零點問題為對應的方程問題,利用分段函數中變量的取值范圍,通過內層方程的求解,由內到外結合外層方程的求解來確定原方程的解,從而可得對應嵌套函數的零點。
解:依題意可令y=f[f(x)]+1=0,所以f[f(x)]=-1。
當x≤0 時,由f(x)=x+1=-1 得x=-2,由f(x)=-2 得x+1=-2 或log2x=-2,解得x=-3或

涉及簡單的嵌套函數的零點問題,可結合內外層函數之間的關系,通過內層函數的整體思維,先內層處理,由內及外,后外層求解,分層分析,分類討論,結合內外層函數所對應的方程,達到解題的目的。整體思維解決嵌套函數的零點問題,是換元解套思維的簡單形式。
二、換元解套,數形結合
對于一些相對復雜的嵌套函數的零點問題,可以將內層函數進行換元處理,通過換元,引入新參數,轉化為新參數的外層函數問題,進而回歸問題本源加以分析與處理。
例 2 已 知 函 數f(x) =則函數y=f[f(x)]-1的零點個數為____。
分析:根據題設條件,化嵌套函數的零點問題為對應的方程問題,通過內層函數的換元處理,結合換元后方程的求解,以及分段函數的圖像來確定對應曲線與直線的交點個數,即確定方程的解的個數,從而得到相應函數的零點個數。
解:依題意可令y=f[f(x)]-1=0,可得f[f(x)]=1。

作出分段函數y=f(x)的圖像,如圖1所示。
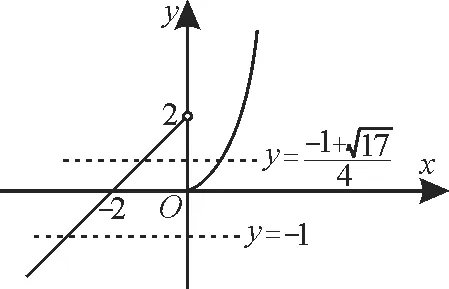
圖1
結合函數y=f(x)的圖像,可知方程f(x)= -1有1 個 解,方 程有2 個解,所以函數y=f[f(x)]-1的零點個數為3。

換元解套是處理嵌套函數的零點問題的主要方法,解答的兩個步驟是:換元解套,通過換元t=g(x),引入參數,則y=f(t),將一個嵌套函數的零點問題巧妙拆解為兩個簡單函數t=g(x)與y=f(t)的零點問題;解方程,利用方程f(t)=0,確定參數t的值,代入方程t=g(x)求出x的值。在利用換元解套思維解題時,可借助函數的圖像進行數形結合,從而達到直觀處理問題的目的。
三、逆向思維,參數范圍
解決一些含參數的嵌套函數的零點問題,可以通過整體思維應用或換元解套思維突破,加以合理的逆向思維,結合圖像的直觀分析來確定參數的取值范圍。
例3已知函數f(x)=-x2-2x,函數若函數y=g[f(x)]-a有4個不同的零點,則實數a的取值范圍是_____。
分析:根據題設條件,化嵌套函數的零點問題為對應的方程問題,利用函數y=f(x)的值域,結合內層函數的換元處理,確定外層函數y=g(t)(t<1)與y=a的圖像的交點個數,從而借助數形結合來確定對應參數的取值范圍。
解:由題意知函數y=g[f(x)]-a有4個不同的零點,所以方程g[f(x)]-a=0有4個不同的實數根。
令t=f(x)=-x2-2x=-(x+1)2+1≤1,由方程g[f(x)]-a=0,可得方程g(t)=a(t≤1)有4個不同的實數根。
易知方程f(x)=t在t∈(-∞,1)內有2個不同的實數根,即函數y=f(x)=-x2-2x與直線y=t(t<1)有2個不同的交點,所以方程g(t)-a=0有4個不同的實數根等價于函數y=g(t)(t<1)與y=a的圖像有2個不同的交點。
當x>0時,=1,當且僅當時,等號成立。
畫出函數y=g(t)(t<1)的圖像,如圖2 所示。結合圖像可知當時,函數y=g(t)(t<1)與y=a有2 個 不 同的交點,所以實數a的取值范圍是

圖2

解決含參數的嵌套函數的零點問題,可借助整體思維或換元解套思維來分析內外層函數的圖像與性質,通過分離參數,結合對應的圖像來確定參數的取值范圍。利用數形結合分析參數的取值范圍時,要注意圖像的關鍵點(如區間的端點、函數的極值點等)的位置關系,從而加以合理的取舍。

(多選題)已知x0是函數f(x)=ex+x-2的零點(其中e=2.71828…為自然對數的底數),下列說法正確的是( )。
A.x0∈(0,1) B.ln(2-x0)=x0
C.x0-e-x0<0 D.>e
提示:對于A,函數f(x)=ex+x-2為增函數,則f(0)=-1<0,f(1)=e-1>0,所以零點x0∈(0,1),A 正確。對于B,x0是方程f(x)=ex+x-2的零點,則ex0+x0-2=0,變形可得ex0=2-x0,兩邊同時取對數得ln(2-x0)=x0,B 正確。對于C,x0是函數f(x)=ex+x-2 的零點,則ex0+x0-2=0,即x0=2-ex0,所以x0-e-x0=2-ex0-e-x0=2-(ex0+e-x0)。又x0∈(0,1),所以ex0+e-x0>2,所以x0-e-x0<0,C 正確。對于D,x0∈(0,1),所以2-x0∈(1,2),所以x2-x00<1

