分析錯因加強防范
■蒙春鳳
指數函數與對數函數是重要的基本初等函數,指數函數與對數函數的圖像與性質容易混淆,因此,解題時稍有不慎就會出錯。下面就此類問題,舉例分析錯因,加強防范意識。
例1化簡:(1-a)[(a-1)-2·

防范措施:化簡指數式時,應討論其中字母的取值范圍,通常根據指數冪的指數來討論,也可以化為根式,利用偶次方根的被開方數為非負數,奇次方根的被開方數是任意實數求出其中字母的取值范圍。如(am)n=amn,當a>0時,(am)n=amn成立;當a<0,m為偶數時,
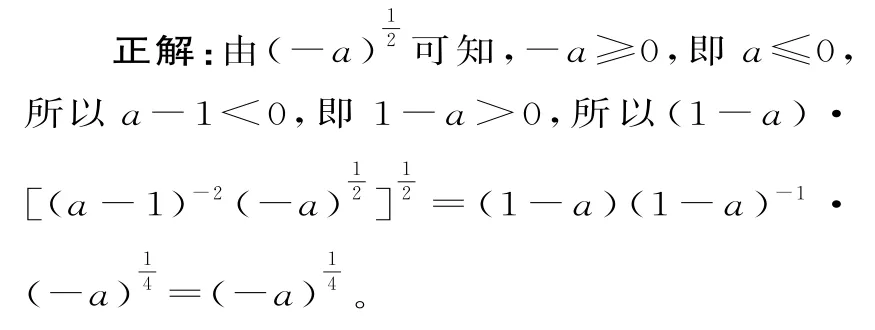
二、忽視對指數函數的底數a 的討論
例2求函數且a≠1)的定義域。
錯解:要使此函數有意義,需滿足ax-1≥0,即ax≥1,解得x≥0。
錯因分析:解不等式ax≥1時,結合指數函數的單調性,需對底數a進行分類討論。上述錯解默認了底數a>1。
防范措施:對涉及含參數的不等式問題,要注意對參數進行分類討論。
正解:要使此函數有意義,需滿足ax-1≥0,即ax≥1。
當a>1時,可得x≥0;當0 綜上可得,當a>1時,函數的定義域為[0,+∞);當0 錯因分析:換元時,要結合指數函數的性質,確定t的取值范圍。 防范措施:在進行換元變換時,一定要等價換元,也就是換元后一定要確定新變量的取值范圍,否則,換元后的變量與原變量不等價,從而產生錯誤結果。 例4解方程log3(x2-10)=log3(3x)。 錯解:原方程可化為x2-10=3x,即x2-3x-10=0,解得x=-2 或x=5。故原方程的解為x=-2或x=5。 錯因分析:上述錯解忽視了對數的真數為正的情況。 防范措施:解關于對數方程或對數不等式時,一定要等價轉化,注意對對數的真數大于0的檢驗。 正解:原方程可化為 由x2-10=3x得x=-2或x=5。 由3x>0得x>0,由x2-10>0得x>或x<-。 經檢驗知x=5符合題意,所以原方程的解為x=5。 例5已知lgx+lgy=2lg(x-2y),則的值的集合為( )。 A.{2} B.{0,2} C.{4} D.{0,4} 錯因分析:上述解法忽視了對數的真數大于0的限制。 防范措施:熟練掌握對數的運算法則是解題的關鍵。解答與對數有關的問題時,必須注意對數式本身的限制條件。 正解:由已知可得lg(xy)=lg(x-2y)2,所以xy=(x-2y)2,整理得x2-5xy+4y2=0,即(x-y)(x-4y)=0,所以x=y或x=4y。 由x>0,y>0,x-2y>0,可得x>2y>0,所以x=y(不合題意,舍去),所以x=4y,即 例6求函數的定義域和值域。 錯解:由題意可得-lg(1-x)≥0,即lg(1-x)≤0,也即lg(1-x)≤lg1,所以1-x≤1,解得x≥0,所以此函數的定義域為[0,+∞)。 因為-lg(1-x)≥0,所以≥0,所以此函數的值域為[0,+∞)。 錯因分析:上述解法對對數的取值理解不清晰。實際上,當底數a>1時,若logax≤0,則0 防范措施:解答本題時,要注意題中的隱含條件。 正解:由題意知-lg(1-x)≥0,可得lg(1-x)≤0,即lg(1-x)≤lg1,所 以解得0≤x<1,所以此函數的定義域為[0,1)。 因為-lg(1-x)≥0,所以0,所以y≥0,所以此函數的值域為[0,+∞)。三、換元時忽視中間變量的取值范圍


四、解對數方程時,忽視真數的取值范圍
五、對數運算,忽視真數大于0
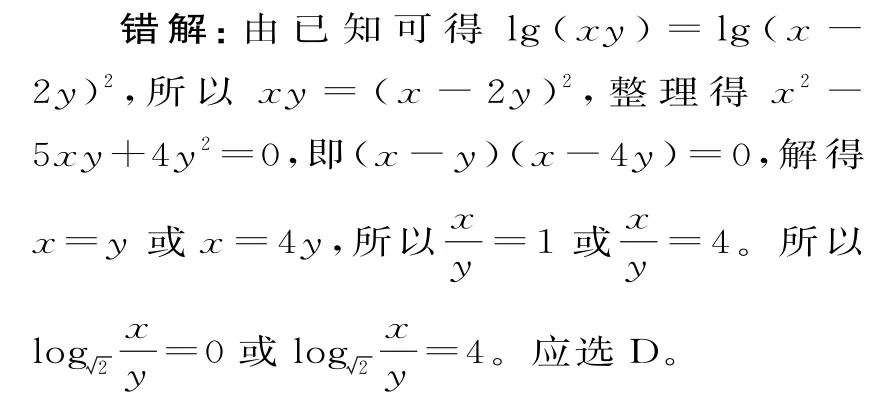
六、求函數的定義域時,忽視對數函數的真數的取值范圍



