基于多尺度數學模型的波束角效應改正方法

胥 洪 川,周 威,孫 振 勇,馬 耀 昌,鄭 亞 慧

(1.長江水利委員會水文局 長江上游水文水資源勘測局,重慶 400021; 2.長江水利委員會 水文局,湖北 武漢 430010)

0 引 言

單波束測深系統由單(雙)頻單波束測深儀、GNSS定位導航系統、測深導航軟件以及測船載體構成,具備操作簡便、成本低廉等特性,是目前水下測量最主要的技術手段。聲學回波的形態由換能器的結構決定,在目前單波束測深技術中,測深儀換能器均是以一定開角的波束發射聲波,這就使得聲學信號是以“錐形”的方式發射至水底。因此,測深儀換能器收到并記錄的信號觸發點為“錐形”水底區域內至換能器的最短距離,這就是測深波束角效應。

水底地形復雜,往往“錐形”下水底區域內至換能器的最短距離并不是測量時的實際水深,從而造成地形變形失真。目前,大量的學者針對波束角效應失真規律及改正方法作了深入研究。在測深儀計算機模擬方向,徐曉晗[1]應用微分幾何的原理對不同類型海底的波束角效應空間結構進行建模仿真,建立失真模型;鄒永剛等[2]利用Matlab語言設計模擬測深儀工作機制,驗證波束角效應測深原理;畢彥等[3]針對單波束測深儀波束角的設計影響因素進行了歸納和分析,對不同波束角情況進行仿真試驗。在原理研究方向,劉雁春[4]、徐曉晗[5]、周志宏等[6]將波束角效應按表現形式分類(傾斜、凹形、凸形),并提出了相應的改正方法、改進模型;鄒永剛等[7]對海底地形中凸形海底的改正方法作進一步補充說明;鄒永剛[8]、肖付民[9]等基于測線方向、海底傾斜角等研究,提出了一些可行的算法;崔曉東等[10]基于這些特性,提出一種針對復雜海底地形的自動改正方法。在姿態改正方向,徐曉晗等[11]論證波浪效應和波束角效應耦合下空間形態與數學描述,推導改正模型。測深實踐中,吳敬文等[12]采用波束角3°、8°的單波束測深儀進行姿態耦合試驗分析,用來提高復雜水域水深測量精度問題。在此基礎上,吳敬文等[13]就波束角效應與測船姿態(Roll、Pitch)耦合的作用效應提出了相應的改進算法;于家城等[14]就多波束系統工作原理進行多波束波束角效應改正實驗,提升測深成果精度。這些學者都提出了較為完善的理論方法,但是這些理論都是波束角效應二維平面下的失真規律,而對于水下地形三維空間下坡度、坡向的探討較少。真實的地形錯綜復雜,測線方向并不能完全代表坡度方向。實際生產中,波束角效應帶來的測深誤差常被忽略。

本文通過對波束角數學改正模型進行展開分析,提出一種基于多尺度數學模型的單波束測深波束角效應改正方法。多尺度數學模型是以水下測點多尺度因子的位置、坡度、坡向、水深、半波束角以及波束角效應的空間表現形態建立的一種波束角效應數學改正模型。該方法利用Horn算法擬合改正模型關鍵尺度水下地形點的坡度、坡向,基于多尺度因子波束角數學改正模型,實現對復雜水域下單波束測深由于波束角效應引起的地形失真的改正。經過試驗定性定量分析,波束角效應帶來的誤差得到改善,測深精度得到一定程度的提高。

1 波束角效應的失真規律

單波束測深儀發射的測深信號受到波束角效應的影響,使得記錄的測深回波圖像失真,測深軟件讀取的水深值與真實的水深值存在偏差[15-16],進而影響測深精度。基于以測深儀換能器“錐形”方式發射的特性,測深儀換能器接收的信號可類比于一個個“腳印”的信號,水底地形的坡度決定了“腳印”的復雜程度[17],水深決定了“腳印”的大小,而換能器波束開角的大小決定了“腳印”的分辨率。因此,波束角效應的影響是由水底地形的坡度、水深以及測深儀換能器自身的波束開角大小共同決定的,水底地形的坡度越大、水深越深、測深儀換能器的波束開角越大,對測深精度影響越大。波束角效應造成水下地形測量精度降低,使得水下地形與實際地形相比趨向平坦。

在二維空間下,人們常常把水下測點按斷面形態分為傾斜、凹形、凸形3種斷面形態點。傾斜斷面形態點是最普遍的一種水下斷面類型點,它表示地形趨勢方向一致的狀態。凹形斷面形態點、凸形斷面形態點正好位于水底形態趨勢變化的過渡處,從形態上看凹形斷面形態點為該小范圍內的最深點,凸形斷面形態點為該小范圍內的最淺點。波束角效應失真規律表現為:傾斜斷面形態點存在一定的時移特征;凸形斷面形態點凸點沒有失真,凸部回波變寬被拉長,呈現一定的雙曲線增偽特征;凹形斷面形態點凹部回波變窄,凹點的失真最大且部分凹部沒有真實回波,凹形斷面形態點最深處深度丟失。

在三維空間中,由于波束角效應所涉及的變化因素較多,對于它影響的研究趨于復雜。測深儀換能器最早接收到的信號極可能是“腳印”里最淺的信號,而該點的三維特征可由該點的坡度、坡向以及水深來概括。

2 波束角效應的數學模型

本文基于三維空間中單波束測深波束角效應測深儀換能器波束“錐形”發射的形態、水下地形三維空間形態,建立如圖1所示基于多尺度因子波束角效應數學模型。圖1中,測深儀坐標為O1(X1,Y1),h為儀測水深值,θ為測深儀波束角大小,δ為O1點在水底地形坡度,β為O1點在水底的坡向方位角。

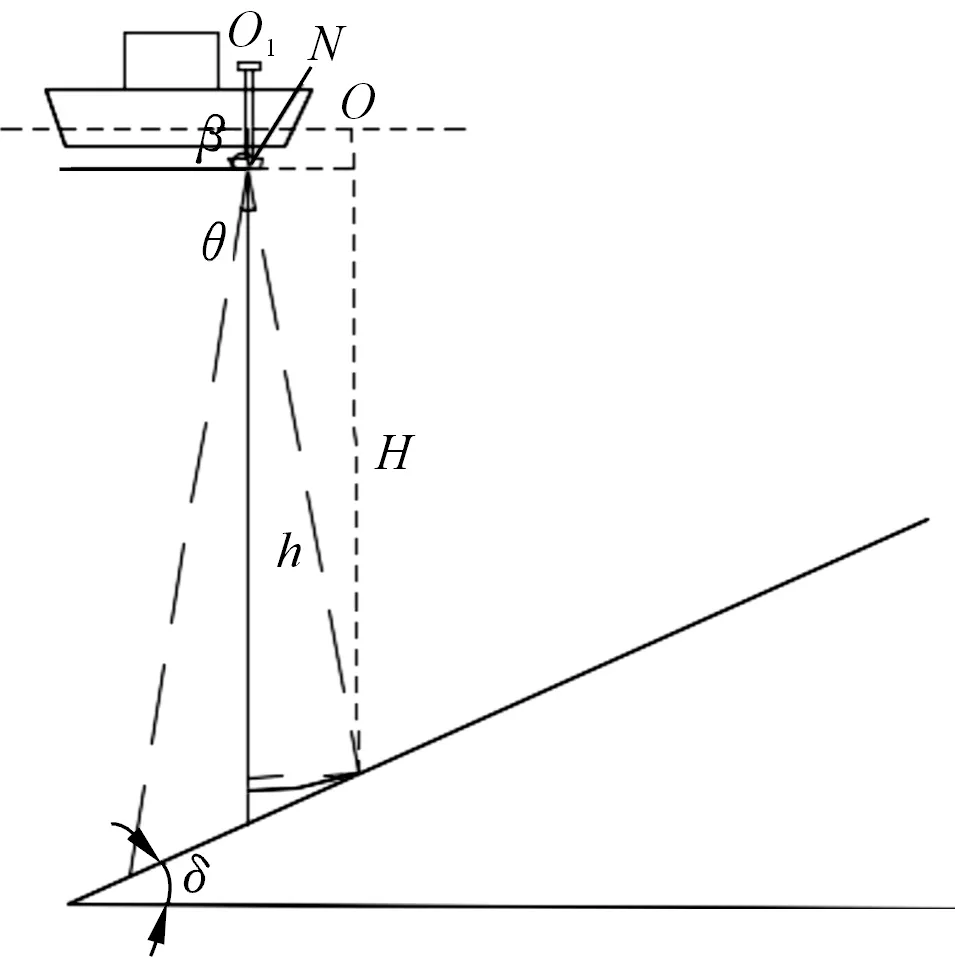
圖1 基于多尺度因子的波束角效應數學模型Fig.1 Mathematical model of beam angle effect based on multi-scale factor

由于波束角效應的影響與測深儀波束開角大小、水底地形坡度密切相關,為得到嚴密的數學改正模型,按以下兩種情況進行討論。

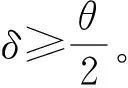
(1)

則O(X,Y,H)點的公式推導為

(2)

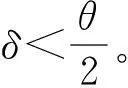
(3)

則O(X,Y,H)點的公式推導為

(4)

3 基于規則格網的坡度、坡向計算

坡度是地表位置上高度變化率的量度,用百分數或者度數表示。坡向是斜坡上最陡下坡傾斜程度上方向的量度,從正北為0°開始,順時針移動,與坐標方位角方向相同,單位為度。

3.1 Ritter算法

Ritter算法空間示意如圖2所示。

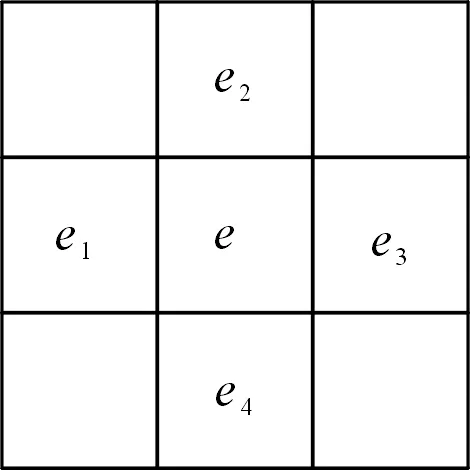
圖2 Ritter算法空間示意Fig.2 Space diagram of Ritter algorithm

Ritter算法采用與中心像元直接鄰接的4個像元,估算中心像元的坡度與坡向。中心點e的坡度:

(5)

中心點e的坡向:

(6)

式中:ei表示相鄰單元值,d代表單元大小,(e1-e3)表示x方向的高差,(e4-e2)表示y方向的高差。

3.2 Horn算法

Horn算法空間示意如圖3所示。Horn算法采用使用8個鄰接像元,4個直接相鄰像元的權重取2,4個對角像元權重取1。則中心點e的坡度:

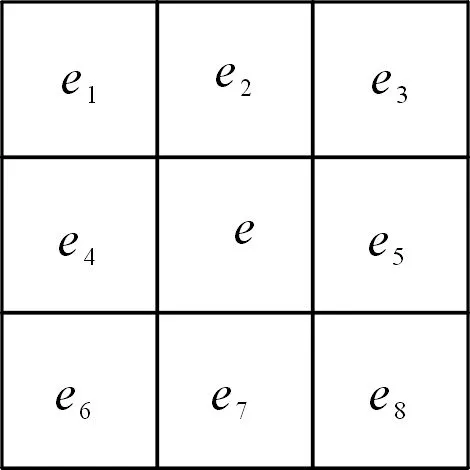
圖3 Horn算法空間示意Fig.3 Space diagram of Horn algorithm

Se={[(e1+2e4+e6)-(e3+2e5+e8)]2+

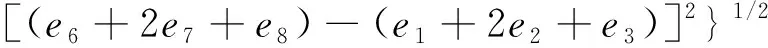
(7)

中心點e的坡向:

(8)

式中:ei表示相鄰單元值,d代表單元大小,(e1+2e4+e6)-(e3+2e5+e8)表示x方向的高差,(e6+2e7+e8)-(e1+2e2+e3)表示y方向的高差。與Ritter算法相比,Horn算法加權考慮了4個對角方向對中心點e坡度坡向的影響,這樣計算的坡度、坡向也更為準確合理。本方法坡度、坡向計算采用Horn算法計算。

4 試驗分析

試驗區域為金沙江烏東德庫區白馬口-龍街河段,烏東德庫區地跨云南、四川兩省,試驗區眾多高山深谷相間并列,地形較為復雜,測區地表植被稀疏,地表覆蓋物主要為砂石、稀疏荒草地。該河段2020年庫區蓄水前為陸上地形,采用了機載激光LiDAR 獲取全域高精度點云數據;蓄水后原陸上地形已被淹沒,采用單波束測量復測水下地形,復測單波束水下地形與機載LiDAR地形重疊區。因機載LiDAR測量精度遠高于單波束測深精度,本文試驗以機載LiDAR點云數據為基準,對重疊區域改正前、后的單波束數據進行對比分析。試驗區平面基準采用CGCS2000坐標系,高程基準采用1956年黃海高程系,高斯3°帶投影,中央子午線102°。水下復測儀器設備為ODOM DF3200 MKⅢ(波束角4°)雙頻測深儀、天寶 R10 GNSS、Hypack測深導航軟件及專用測量船一艘。為保證數據的準確性,測前儀器均經過嚴格比對和校準,性能穩定。

4.1 試驗區坡度、坡向分析

基于試驗區水下測量數據建立規則格網DEM模型,格網大小d為0.1 m(見圖4)。

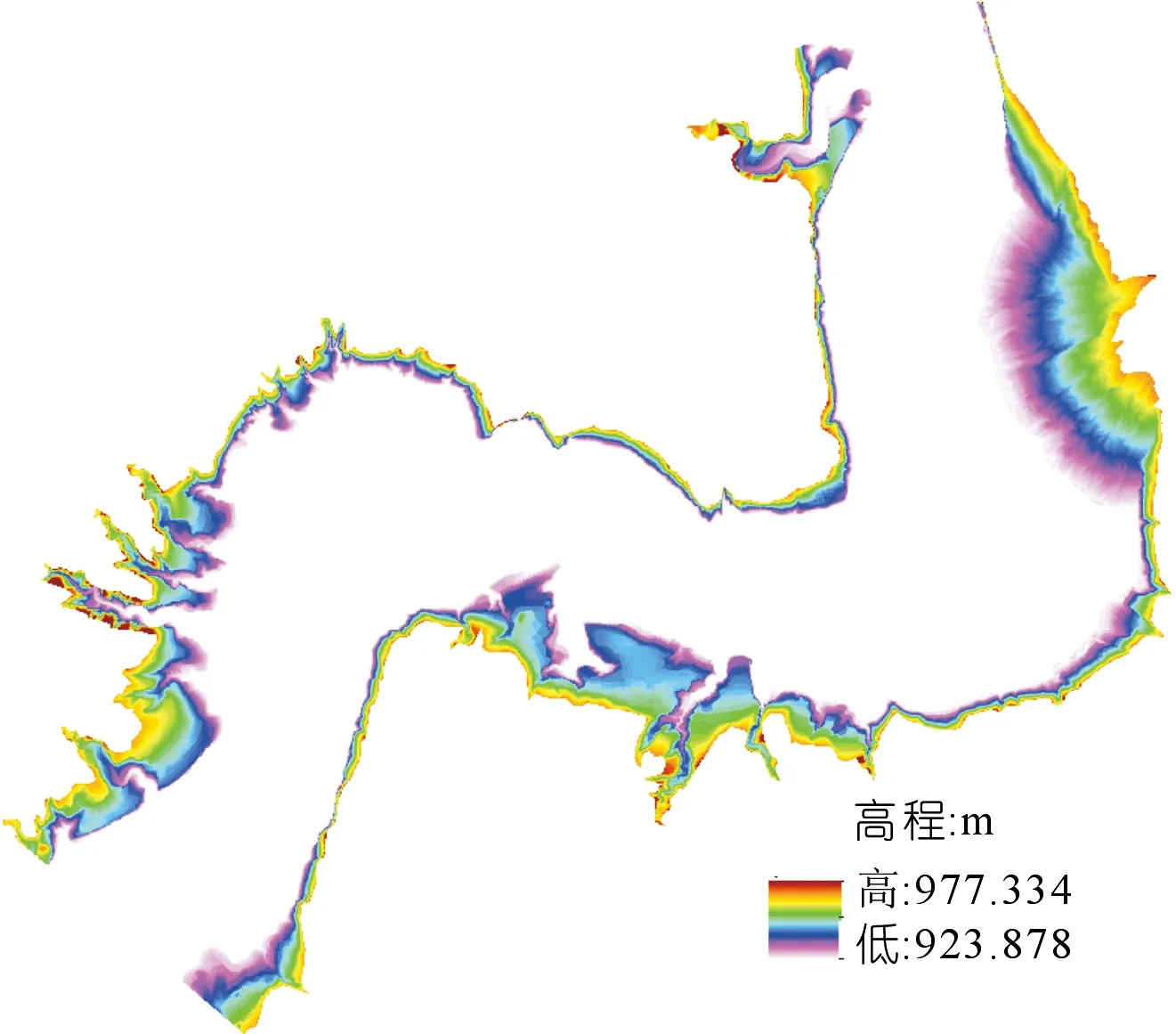
圖4 試驗區DEM模型Fig.4 DEM model of the test area

試驗區規則格網DEM模型基于Horn算法得到試驗區坡度分布圖(見圖5)。該河段屬于山區型河道,兩岸陡坡眾多,最大坡度傾角甚至接近90°。根據波束角效應將嚴重影響水下測深精度。

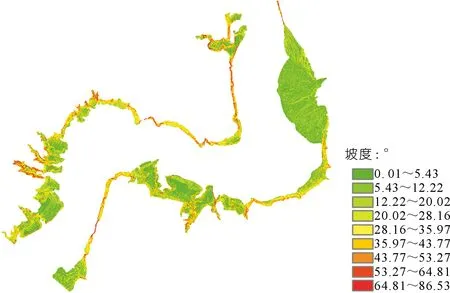
圖5 試驗區坡度分布Fig.5 Slope distribution of the test area

試驗區規則格網DEM模型基于Horn算法得到試驗區坡向分布圖(見圖6)。坡向隨地形分布變化無規律性,難以用一根水下測線來代表兩岸坡向方向。

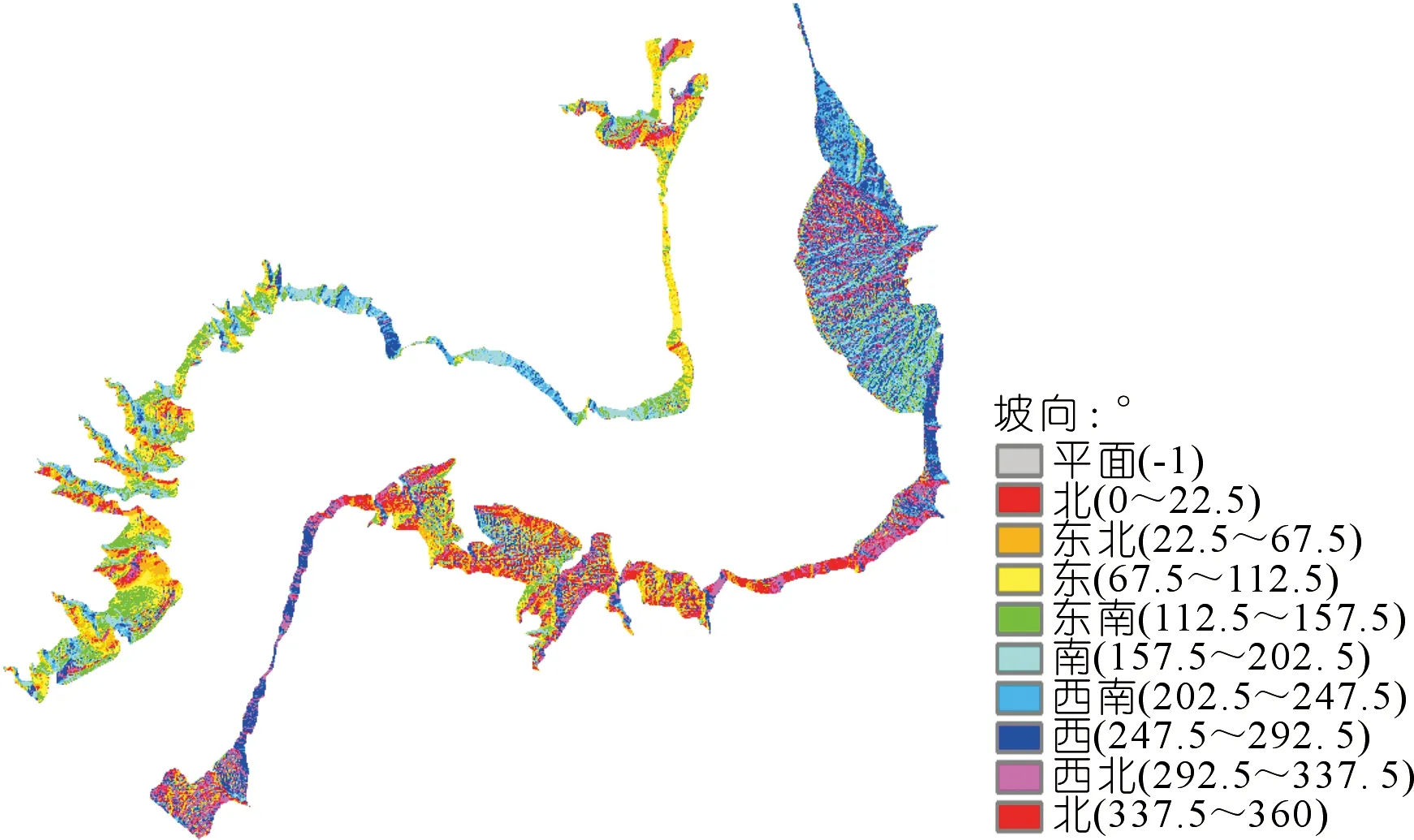
圖6 試驗區坡向分布Fig.6 Slope direction direction of the test area

4.2 試驗區精度分析

原始數據導入到試驗區坡度、坡向分布圖中,通過提取分析得到該數據在空間條件下的坡度、坡向,運用數學改正模型實現波束角效應的改正,部分數據改正前后信息見表1。

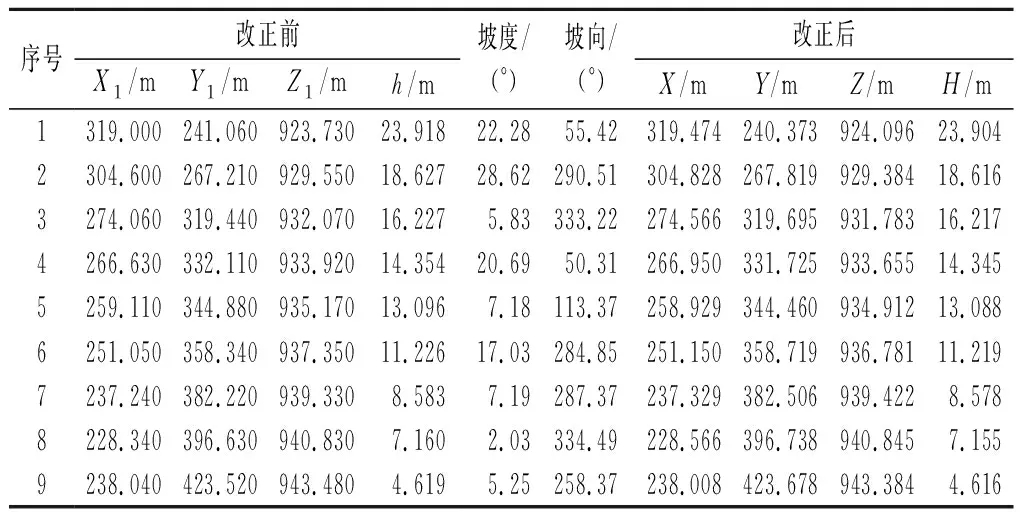
表1 部分試驗測深數據改正Tab.1 Correction of part test bathymetric data

4.2.1較差統計

單波束測深數據樣本1 796個,改正前、后與機載LiDAR點云數據對比較差分布見圖7。由圖7可見,該方法改正前后較差值變化明顯,改正前差值為正的數據占比為55.4%,差值為正數據的數量明顯多于差值為負的數據,與波束角效應把地形測淺的規律相一致;改正后較差主要集中在0.25 m以內,占比為72.2%。改正后在相同絕對值較差情況下([0,0.25]區間除外),區間(-∞,-0.25)與(0.25,+∞)的數量占比分別為8.2%和7.1%,分布圖符合測量隨機誤差的規律。較差[0,0.25]區間內數量占比為57.1%,說明可能還受到其他測量誤差的影響。

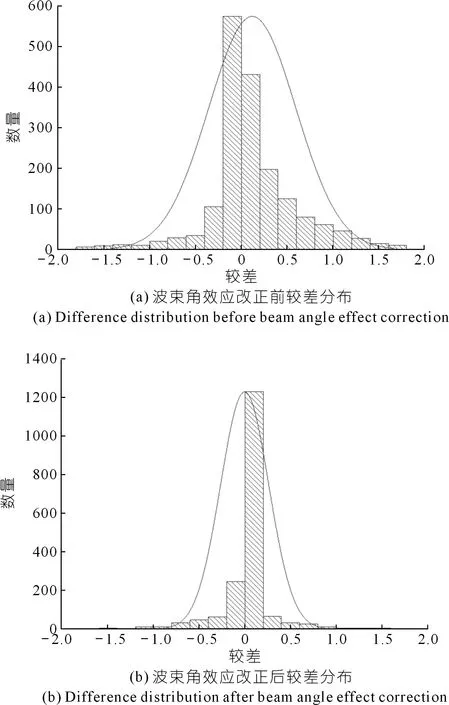
圖7 試驗數據較差分布Fig.7 Distribution of test data difference

4.2.2中誤差統計

中誤差是描述觀測精度較為科學的指標,計算求得中誤差計算公式為

(9)

根據公式(9)求得改正前中誤差為0.49 m,經過波束角效應改正后中誤差為0.25 m,精度提高48.6%。將改正前、后中誤差按不同深度進行統計可得到測深中誤差統計結果,見表2。

表2 測深中誤差統計Tab.2 Mean square error of measuring depth m

從表2可知,改正前水深20 m以內中誤差為0.48 m,水深20 m以上中誤差為0.51 m,改正后水深20 m以內中誤差為0.24 m,水深20 m以上中誤差為0.28 m。經過測深改正后,測量精度也滿足SL257-2017《水道觀測規范》對測深點深度中誤差的要求[18]。

根據不同坡度以及相對應的中誤差統計分析得到坡度-中誤差關系圖(見圖8),根據不同水深以及相對應的中誤差統計得到水深-中誤差統計圖(見圖9)。

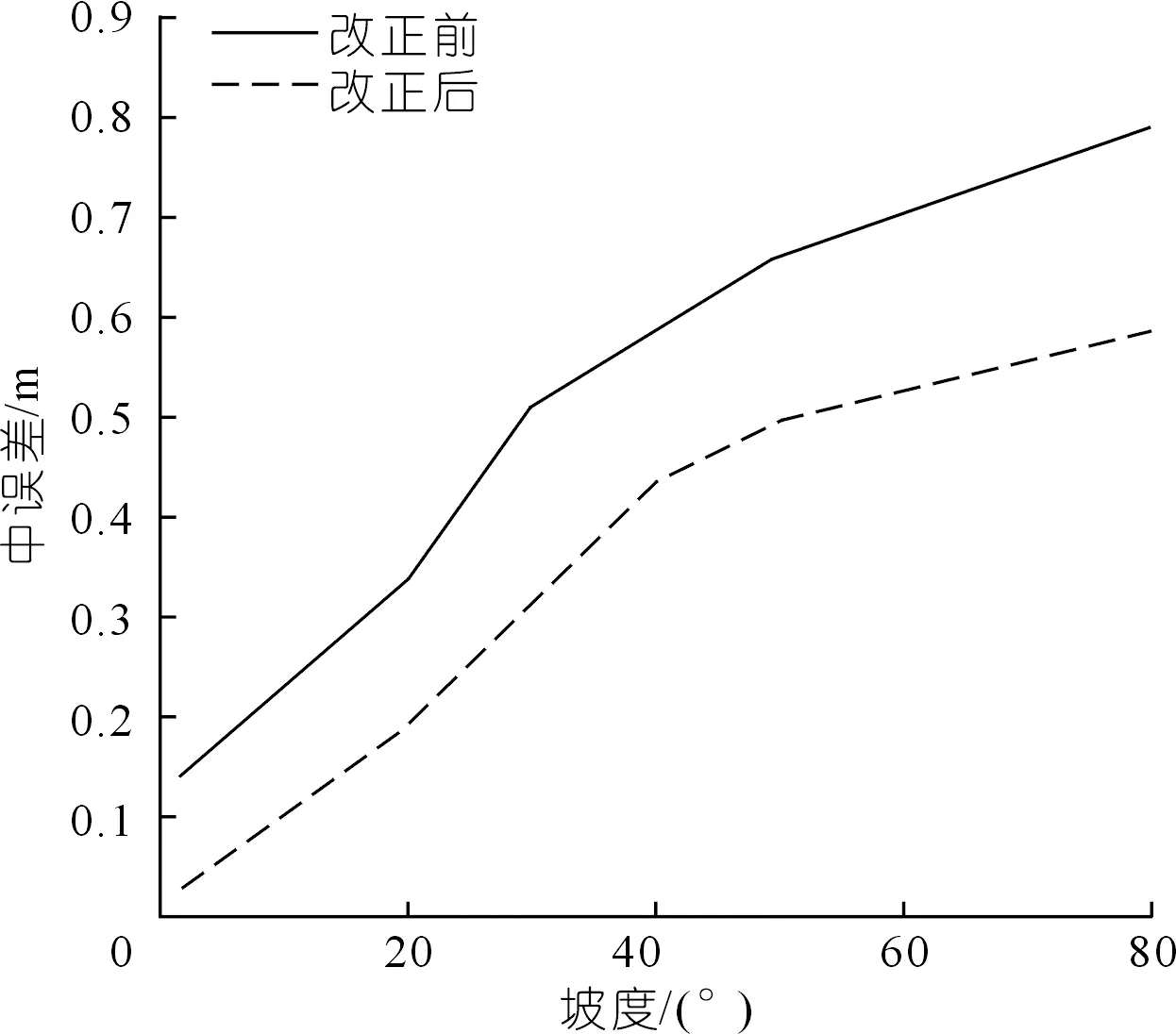
圖8 坡度-中誤差關系Fig.8 Slope-mean square error relationship

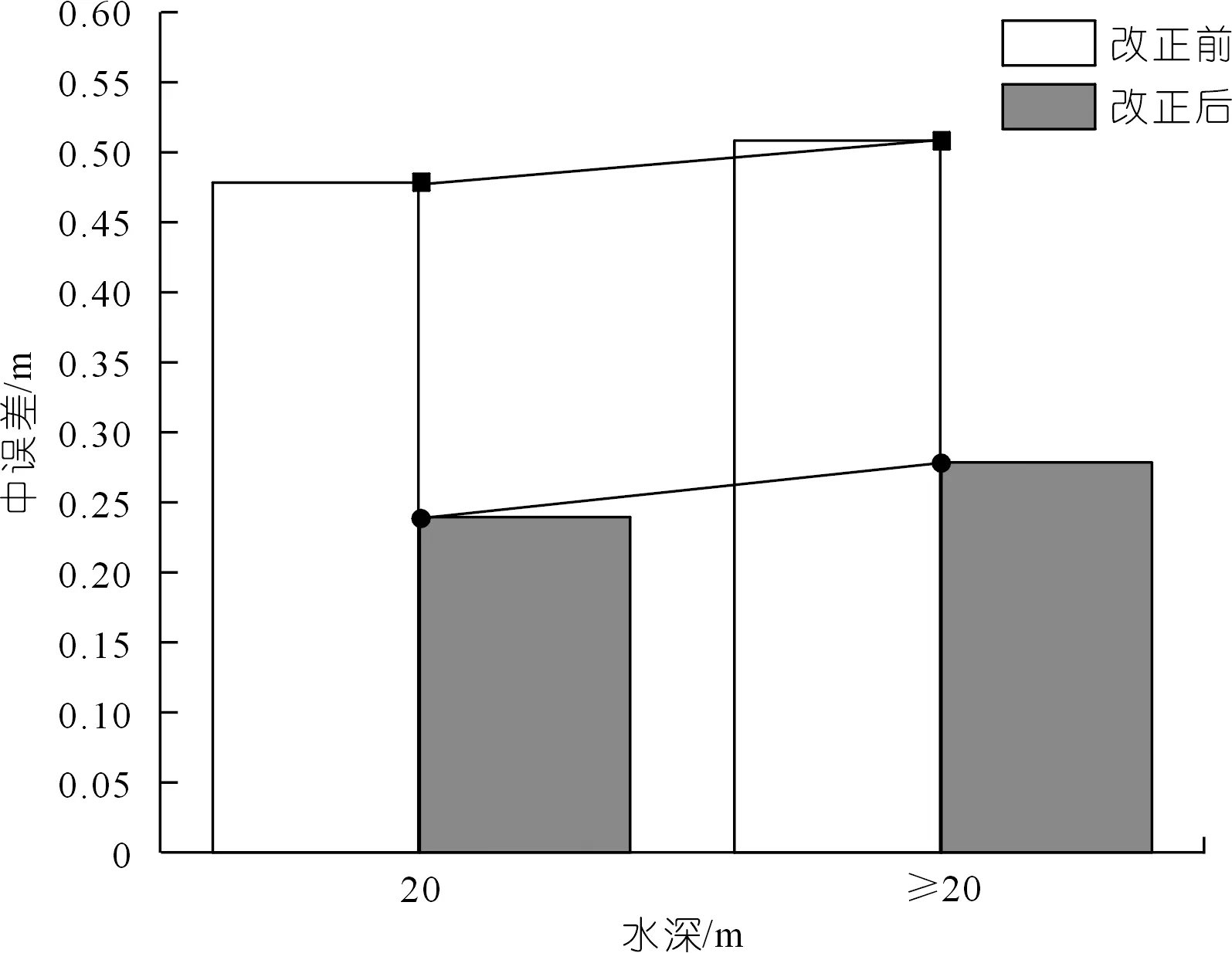
圖9 水深-中誤差統計Fig.9 Statistical chart of bathymetric-mean square error

從圖8中可以得到,隨著坡度的增大,測深中誤差也隨之增大。對比分析坡度、水深與中誤差關系圖,發現深度的綜合影響系數遠小于坡度的影響,坡度與測深中誤差正相關。

5 結 論

本文系統論述了一種基于多尺度數學模型測深波束角改正方法,該方法基于測深換能器波束“錐形”發射的形態、水下地形三維空間形態建立波束角效應多尺度數學改正模型,利用Horn算法擬合改正模型關鍵尺度水下地形點空間上坡度、坡向,實現三維空間下測深波束角效應的改正。經過試驗定性定量分析,結果表明:波束角效應帶來的影響明顯減弱,改正后測深中誤差精度提高48.6%,傾斜地形水下測量的精度得到有效提升;水下地形的坡度是影響波束角效應的主要因素。綜上所述,本方法為波束角效應的改正研究提供了新的方向,對于提高單波束測深精度具有一定的借鑒意義。