基于密度聚類的監測數據漂移動態校正算法
李 鵬 飛,雷 未,虞 冬 冬,吉 同 元
(1.華設設計集團股份有限公司,江蘇 南京 210014; 2.華設檢測科技有限公司,江蘇 南京 210014; 3.河海大學 水利水電學院,江蘇 南京 210098; 4.常州市三級航道網整治工程建設指揮部辦公室,江蘇 常州 213003)
0 引 言
水利工程結構監測是評價工程施工期與運行期安全的重要手段[1-2]。受外界環境干擾、儀器監測故障或是監測系統不穩定等因素影響,部分監測點存在數據異常現象,其中較常見的是監測數據發生區間性的整體漂移。漂移區間的存在,使得監測序列對整個工程安全穩定的評估出現較大偏差。因此,校正監測序列的區間性漂移數據,對實際工程的安全分析具有重要應用價值[3]。
目前常用的漂移校正方法有零變化值法[4]和回歸校正法[5]。前者假定漂移區間中初始漂移點的真實值與上一時刻的觀測值相等,以初始漂移點為基準,將漂移區間整體移動至真實值位置,從而實現對漂移數據的校正。這種方法操作簡單,但要求漂移前后的環境量保持一致,適用范圍有限。后者建立環境量與效應量的回歸關系,結合外部荷載的監測量重新計算漂移點的真實值。該方法邏輯嚴謹,但要求依次對漂移測點建立函數關系,且要具備較為豐富的工程資料,故無法為環境量監測數據缺失的工程提供可靠的校正方案。對于水利工程結構,尤其是混凝土結構來說,監測數據之間往往存在著空間相關性[6]。例如在同一區域或部位的測點,其監測序列呈現出相似甚至一致的變化規律[7]。基于這種相似性,可以為某一測點的漂移校正量提供參考依據。因此,通過對相似測點的監測序列進行融合分析,探究監測量的主體變化規律,從而可以判定出某一測點的漂移區間和漂移量。這種融合方式可以采用聚類分析算法來實現[8]。
隨著人工智能技術與機器學習算法的發展,水利工程安全監測智能化已取得重大突破[9-10]。聚類分析作為一種無監督學習方法,常被用于將目標對象分為不同的簇[11-12]。通過對目標的距離或相似度進行定義,保持簇內的最小距離或最大相似度,以實現“物以類聚”[13]。總體來說,聚類算法主要可分為球形互斥簇劃分法(如K-means)[14]、層次聚類方法[15]、基于密度的聚類方法(如DBSCAN)[16-17]以及基于模型的聚類方法(如EM)[18]等。其中,球形互斥簇劃分法適用于發現類球形的簇,對于中小規模數據集有效;層次聚類方法用于展示對象間距離的層次關系;基于模型的聚類方法形成的是對象的“軟聚類”(即對象屬于各個簇的概率)。密度聚類方法的指導思想是,只要樣本點的密度大于某閾值,則將該樣本點添加到最近的簇中。DBSCAN算法是一種典型的密度聚類方法,適用于不需要預先設定聚類數量的分類任務[19]。由于存在最小點數的限制,這種算法能克服基于距離的算法只能發現“類球形”(凸)的聚類(如K-means)的缺點,可發現任意形狀甚至是無連接的環狀對象的聚類,且對噪聲數據不敏感[20]。因此,該算法在監測序列聚類分析過程中可以靈敏捕捉漂移數據點。
本文提出一種基于密度聚類的動態漂移校正模型,采用DBSCAN算法判定漂移區間,滑動窗口模式動態校正測量序列的漂移數據。這種方法充分利用測點間的相互關聯性,較為完整地保留監測序列自身的變化規律,并可以實現高精度自動校正。
1 測點融合的漂移校正原理
漂移是指監測儀器計量特性的變化引起的示值在一段時間內的連續或增量變化,這種變化既與監測量的變化無關,也與環境量的變化無關。水工結構監測點之間具有顯著的空間關聯性。例如,不同區域測點之間的變形規律存在差異,而同一區域內的測點變形規律相似程度更為接近。因此,當某個測點的測值發生數據漂移時,可以考慮融合附近測點的監測序列,依據其變化規律對漂移區間進行判定并校正。
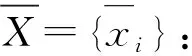
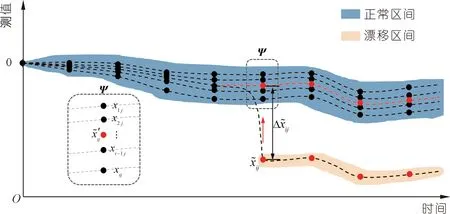
圖1 測點融合的漂移校正示意Fig.1 Schematic diagram of drift correction for monitoring points fusion
(1)
(2)
式中:k為Ψ內數據點數目。
(3)
(4)
待監測序列進行漂移分析并校正后,按式(5)對序列還原其起始值:
(5)
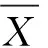
2 基于密度聚類的動態校正算法
測點融合校正法的內核是找出相似度更高的監測序列集合,其相似度最直觀的定義就是距離,距離越靠近的監測數據點就越容易被劃分為同一集合。當監測序列發生漂移時,漂移數據點遠離正常區間數據,從而形成新的集合。這種對數據點集分布最直接的劃分手段就是聚類分析算法,其中密度聚類算法適用于發現時間序列帶狀的點集聚類。
2.1 DBSCAN密度聚類
DBSCAN算法是一種基于密度的聚類算法,與劃分和層次聚類算法不同,它將簇定義為密度相連點的最大集合,能夠把具有足夠高密度的區域劃分為簇,并可在有“噪聲”的數據中發現任意形狀的聚類。該算法涉及兩個參數:數據點鄰域半徑ε和最小鄰域點數目閾值MinPts。以某數據點為中心,ε為半徑所覆蓋的范圍稱為該點的ε-鄰域。故而該算法將數據集D內的數據點分為核心點、邊界點和噪聲點3種類型。若ε-鄰域內數據點個數超過MinPts,稱為核心點;ε-鄰域內數據點個數不超過MinPts,稱為邊界點,既非核心點也非邊界點的數據點稱為噪聲點。同時也將數據點之間的密度關系分為直接密度可達、密度可達和密度相連3種(見圖2)。
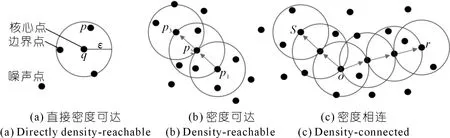
圖2 數據點之間密度關系Fig.2 Density relationship between data points
(1) 直接密度可達:對于給定的數據點集D,如果p在q的ε-鄰域內,且q是一個核心點,則稱p從q出發是直接密度可達的。
(2) 密度可達:對于一個數據鏈p1,p2,…,pn(pi∈D),若pi+1到pi是關于ε和MinPts直接密度可達的,則稱p1到pn是關于ε和MinPts密度可達的。
(3) 密度相連:如果數據集D中存在數據點o,使得o到r和s都是關于ε和MinPts密度可達的,則稱r和s是關于ε和MinPts密度相連的。
DBSCAN算法先提取出數據點集中的核心點,再隨機選擇一個核心點作為“種子”,通過密度可達性逐步向外發散,進而找到最大的密度相連區域,具體步驟如下:
(1) 輸入樣本數據集D={x1,x2,…,xm},定義鄰域半徑ε和點數閾值MinPts。
(2) 遍歷樣本數據點,確定樣本點xi(i=1,2,…,m)的ε-鄰域內的所有節點。若ε-鄰域節點數不小于MinPts,則xi為核心點,整合所有核心點集合為Ω。
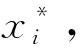
(4) 重復步驟(3)的操作,直到Ω中不再存在未被訪問的核心點。D中未被聚類的數據點標記為噪聲點。
2.2 監測量漂移動態校正模型
2.2.1密度聚類一般校正方法存在的問題
基于第一章所闡述的校正方法,采用密度聚類算法對測點序列進行融合分析。它理論上可以實現對漂移區間的判定和校正,但在實際操作中可能存在校正突變和類簇粘連的問題。
在上述校正過程中,當發生偏移的監測序列處于集合邊緣,初始漂移點以相關測點同一時刻觀測值的落點中心為實際校正位置。Ψ的密度中心值與“理想”校正值之間存在偏差,從而導致校正后的測值曲線會發生突變現象(見圖3(a))。此外,同一測點的傳感器受多次外界干擾后,其測值曲線也可能存在著多個漂移點,需要進行多次測點漂移校正。
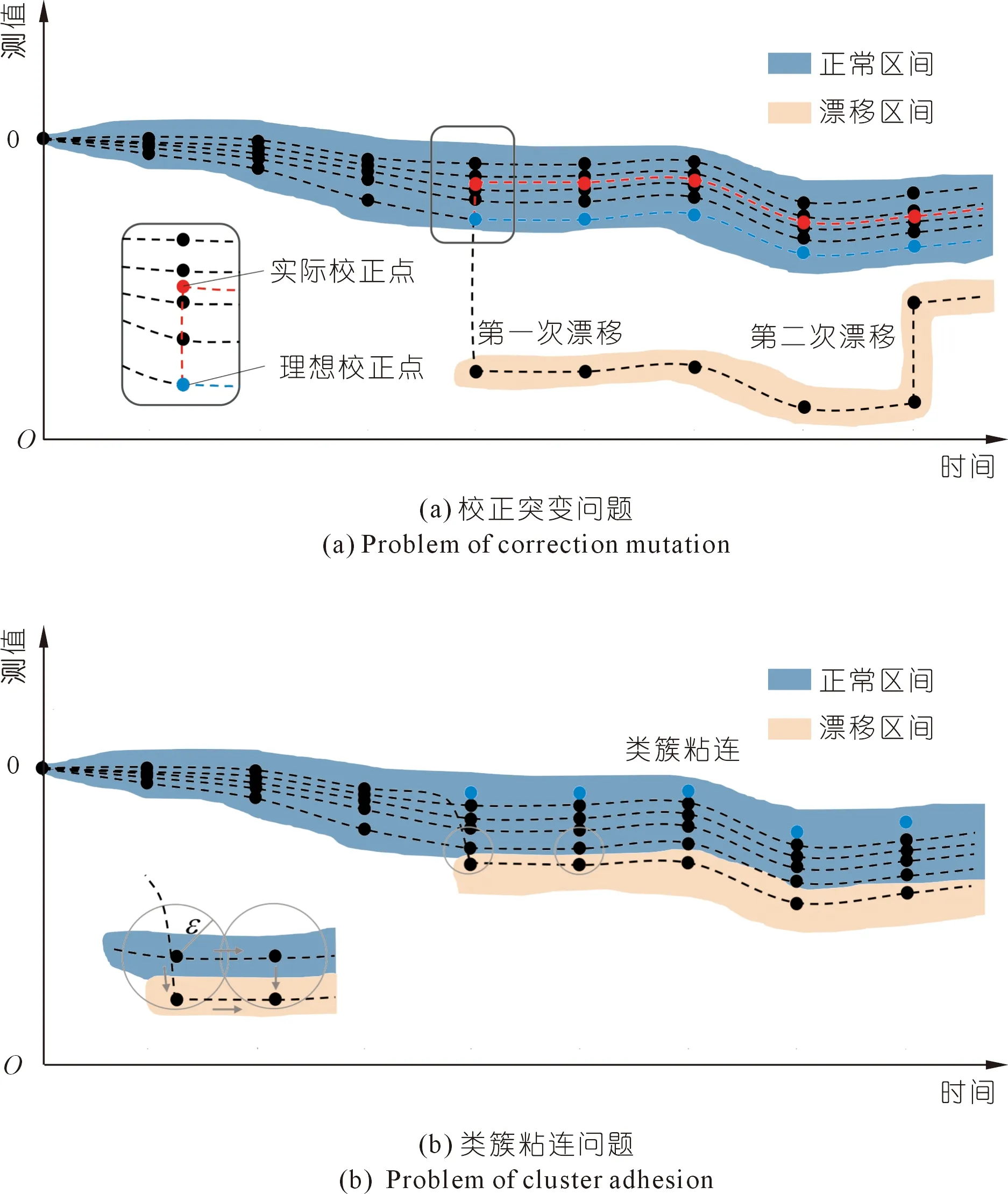
圖3 基于密度聚類的漂移校正方法存在的問題Fig.3 Problems of drift correction method based on density clustering
同時,DBSCAN算法是以尋找密度相連最大點集為核心,由此判別出監測數據的正常區間與漂移區間。當監測序列的漂移區間與正常區間距離較小,可能發生類簇粘連的現象(見圖3(b))。此時漂移點處于其鄰近正常點的ε-鄰域內,DBSCAN算法則判定漂移點仍屬于正常區間,從而無法識別出監測序列的漂移區間。
為了解決上述現象所產生的校正問題,本文提出一種基于密度聚類的監測量漂移動態校正模型,采用滑動窗口模式來對測點進行漂移校正。
2.2.2基于滑動窗口模式下的動態校正過程
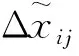
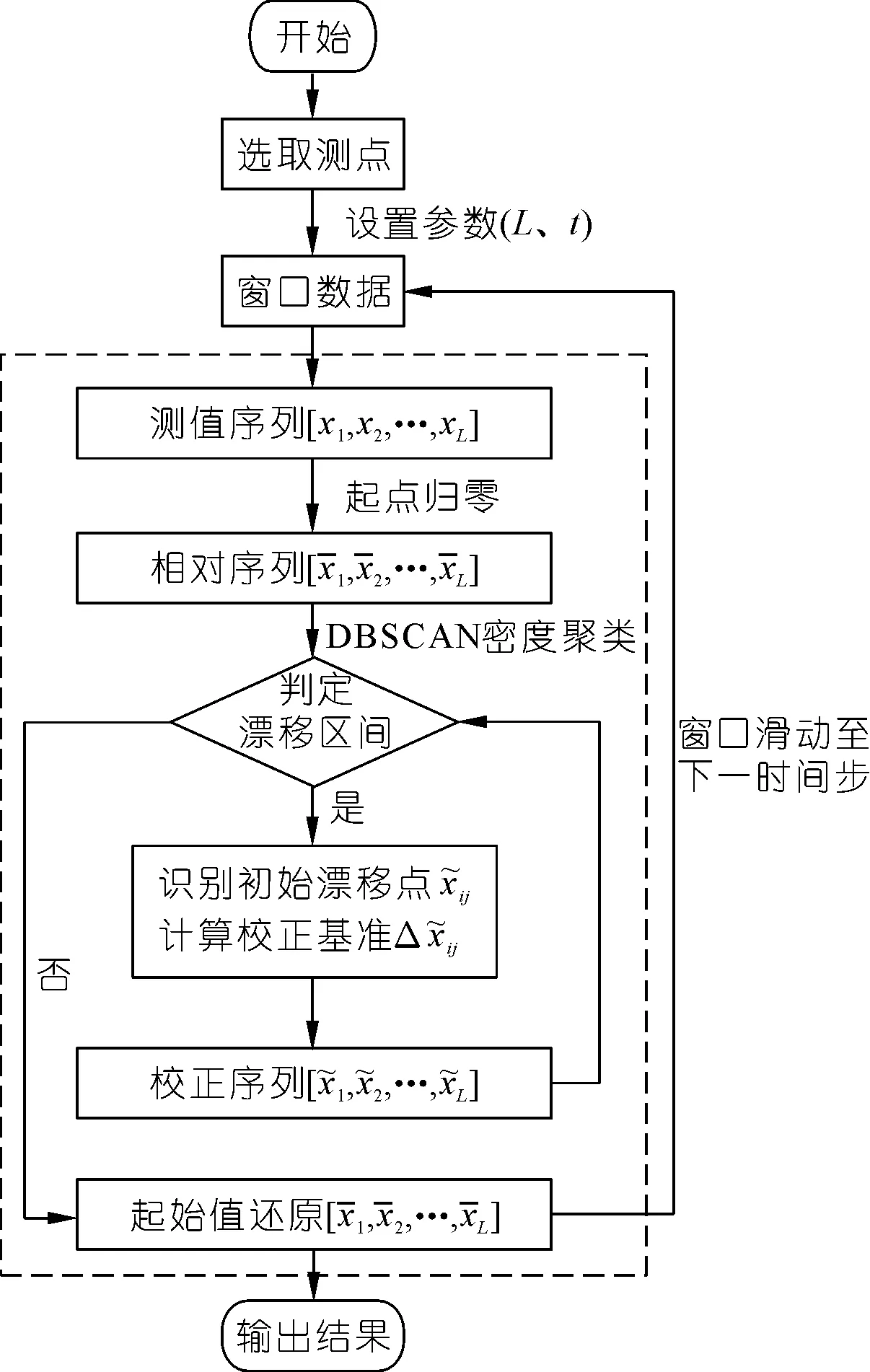
圖4 基于密度聚類的監測量漂移動態校正模型Fig.4 Dynamic correction model of monitoring drift based on density clustering
(1) 選取同區域測點的測值作為待分析的時間序列,在時間序列起始時刻點設置尺寸為L的滑動窗口,則窗口內的測值序列為[x1,x2,…,xL]。
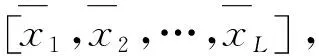
(3) 窗口的滑動校正。設定窗口滑動時間步為t(t≤L),滑動窗口至下一個時間步,重復步驟(2)的操作。
3 有效性測試
為驗證本文提出的漂移校正模型性能,選取某渡槽工程的槽身腰部外壁應力監測結果為研究對象,對其部分測值進行漂移處理后,采用校正模型校正漂移區間,并將校正結果與實際結果進行對比,驗證模型的有效性。
3.1 工程概況
某大型U型輸水渡槽采用預應力簡支結構,跨度42 m,設計流量92 m3/s。槽身采用C50預應力混凝土澆筑,為驗證設計并指導施工,開展了1∶1原型試驗,布置鋼筋計、應變計監測槽身應力應變。圖5展示了渡槽監測斷面與儀器分布示意圖,儀器命名規則如下:[儀器類型][布置斷面]-[儀器編號](R代表鋼筋計,S代表應變計;如R2-1代表2-2斷面1號鋼筋計)。應變單位為με,應力單位為MPa。
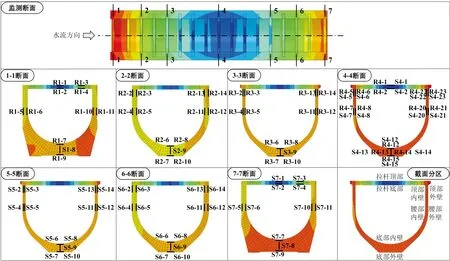
圖5 監測斷面與儀器布置Fig.5 Monitoring sections and instruments layout
3.2 數據預處理
選取該渡槽5月30日至9月18日的槽身腰部外壁應力監測數據作為驗證對象。由于實際監測資料為非等間隔觀測,測點同時刻數據存在缺失情況,因此本文采用線性插值技術將其變為等間隔時間序列,以適應校正模型的需要。如圖6所示,每隔半小時取一組插值數據,則監測數據被規整為5 300組插值數據。假定監測斷面3-3的腰部外壁應力(R3-4)于6月9日發生一次測量漂移,監測斷面4-4的腰部外壁應力(R4-7)于7月21日與8月11日發生2次測量漂移。采用滑動窗口模式下的密度聚類校正方法來對預設的漂移點進行校正處理。
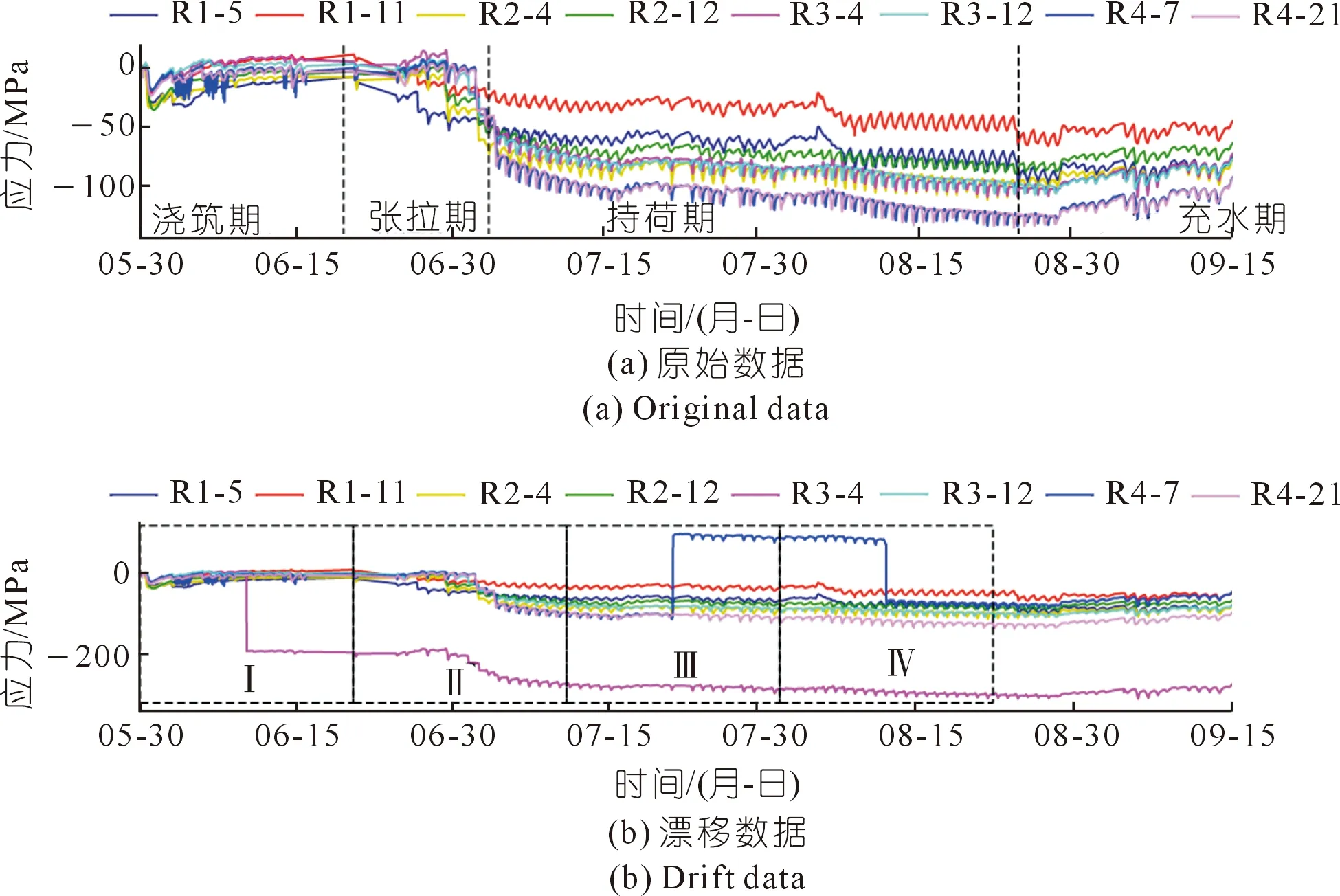
注:應力測值拉為正,壓為負。渡槽于7月初由張拉期進入持荷期,受溫度總體升高(鋼筋膨脹系數大于混凝土)以及混凝土受壓徐變等因素影響,鋼筋的壓應力表現為增大的趨勢,因此所有測點的測值均呈現下降趨勢,非漂移現象。圖6 槽身腰部外壁應力漂移Fig.6 Stress drift on the outer wall of groove waist
3.3 校正過程
本次設定滑動窗口尺寸與滑動時間步均為1 000,則滑動窗口可分4步完成校正過程(見圖6)。圖7展示了窗口4步校正結果。以Ⅰ號窗口為例(見圖7(a)),將窗口內序列起點歸零,采用DBSCAN算法進行密度聚類分析,由此判定漂移區間并識別初始漂移點。檢索與初始漂移點同一時刻的正常數據點集,計算其密度中心點。以初始漂移點為基準,將初始漂移點后的序列(包含初始漂移點)移動到密度中心,完成第一次漂移校正。再次使用DBSCAN算法對窗口內的校正序列進行密度聚類分析,結果顯示無漂移區間(Ⅰ-1號窗口,見圖7(b))。最后還原校正序列起始值,至此實現Ⅰ號窗口內數據的漂移校正過程。窗口繼續滑動至Ⅱ號位置,將窗口內序列起點歸零并進行DBSCAN聚類分析,結果顯示無漂移區間(見圖7(c))。因此,該窗口內無需要校正的漂移點,還原序列起始值。依此類推,窗口滑動至Ⅲ、Ⅳ號位置,完成所有漂移區間的校正過程。
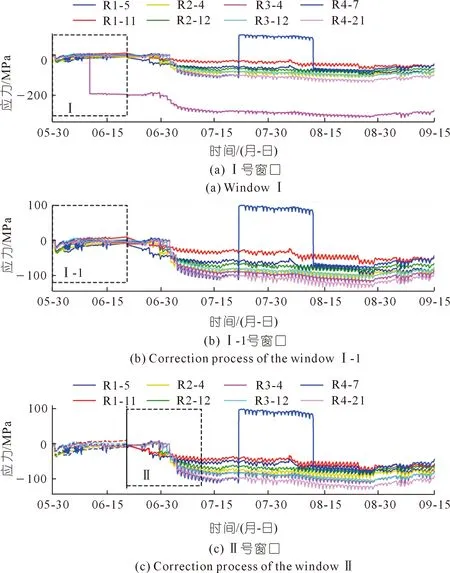
圖7 槽身腰部外壁應力校正過程Fig.7 Correction process of stress on the outer wall of groove waist
3.4 校正結果

表1 槽身腰部外壁應力漂移校正誤差Tab.1 Correction error of stress drift on the outer wall of groove waist
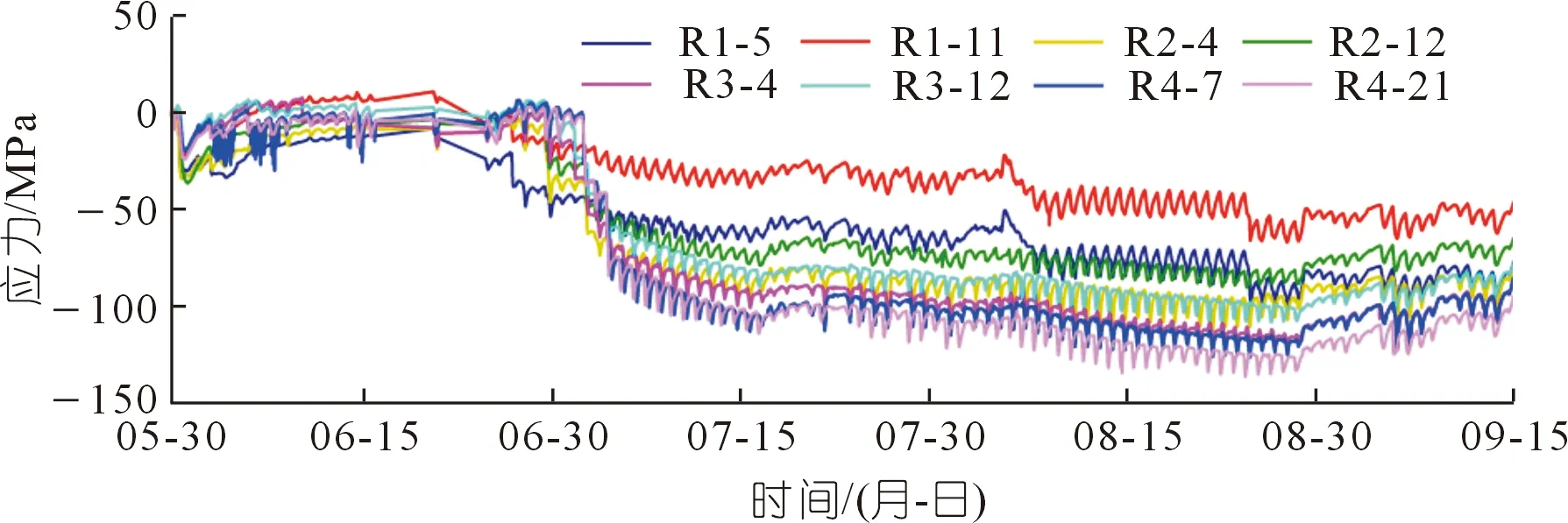
圖8 槽身腰部外壁應力漂移校正結果Fig.8 Correction result of stress drift on the outer wall of groove waist
4 案例校正
采用上述渡槽工程各斷面腰部外壁布置應力計進行各時段應變監測,其變化曲線如圖9所示,其中3支應變計在澆筑期發生測量漂移現象。采用2.2節的校正模型對渡槽監測斷面腰部外壁應變漂移進行校正。如圖10所示,設定窗口尺寸為1 500,將Ⅰ號窗口內序列起點歸零,并采用DBSCAN算法進行密度聚類分析。判定S5-4、S6-4與S7-11這3個測點發生漂移現象,識別各測點的初始漂移點。依照模型操作流程,以初始漂移點為基準,將初始漂移點后的序列(包含初始漂移點)移動到密度中心,完成第一次漂移校正。然后使用DBSCAN算法對窗口內的校正序列進行密度聚類分析,判定S5-4與S7-11仍存在漂移區間(Ⅰ-1號窗口)。同樣依據流程,再次將漂移區間移動到正常序列密度中心,完成第二次漂移校正。此時,基于DBSCAN算法顯示窗口內再無漂移區間(Ⅰ-2號窗口),最后還原校正序列的起始值。因此,Ⅰ號窗口共經歷了兩次校正過程。此時,渡槽監測斷面腰部外壁應變漂移已全部實現校正,校正結果如圖11所示。在后續的監測期內,只要將窗口沿時間軸滑動,就能繼續校正測點的漂移區間。
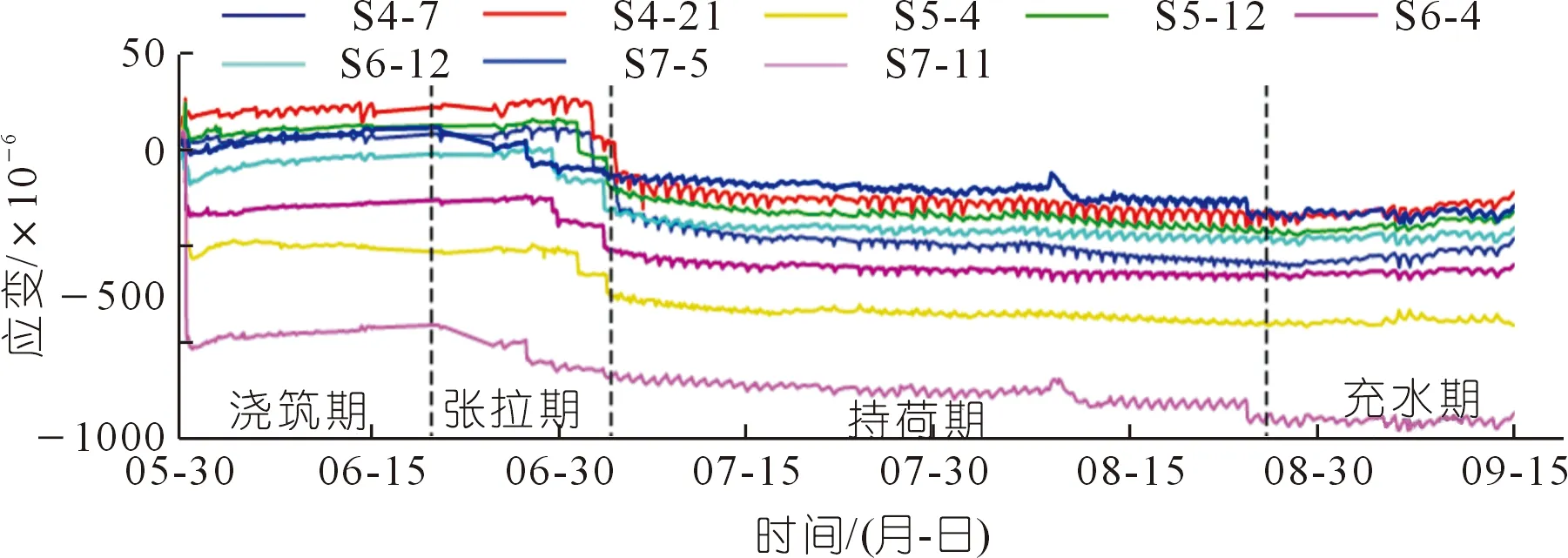
圖9 槽身腰部外壁應變曲線Fig.9 Strain curves on the outer wall of groove waist
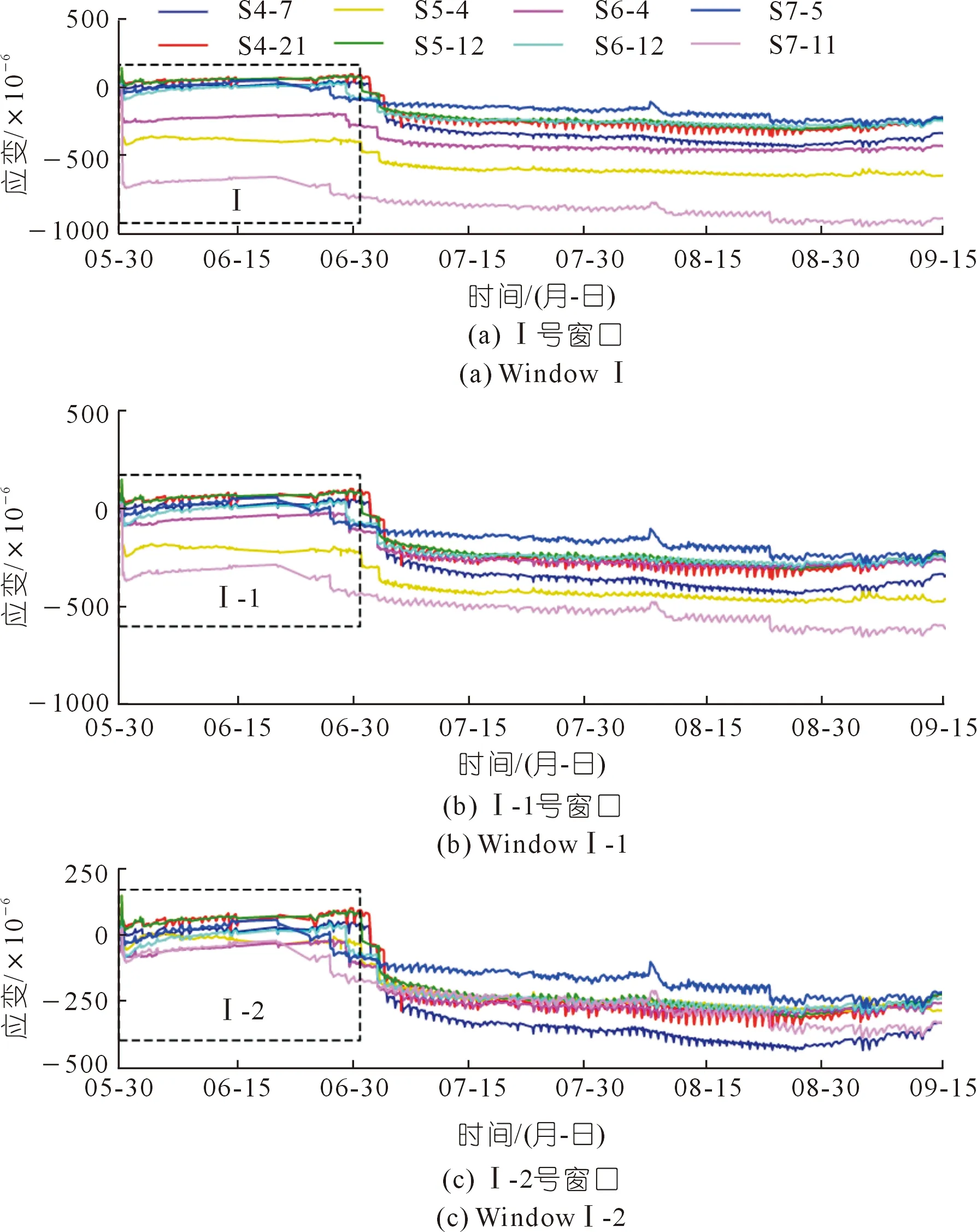
圖10 槽身腰部外壁應變校正過程Fig.10 Strain correction process on the outer wall of groove waist
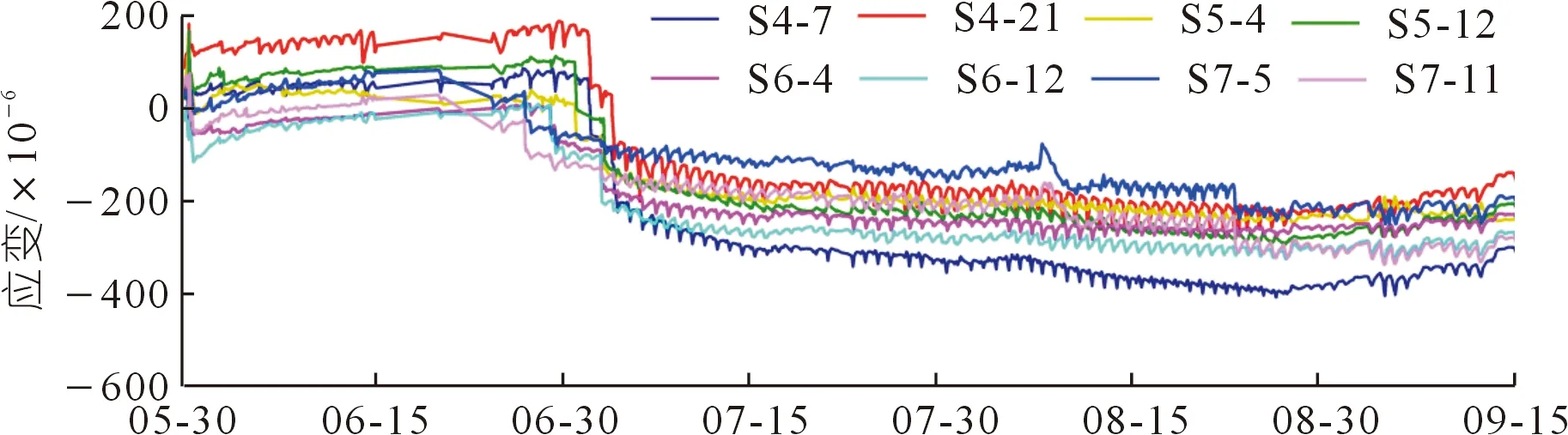
圖11 槽身腰部外壁應變漂移校正結果Fig.11 Correction result of strain drift on the outer wall of the groove waist
5 結 論
本文從水工建筑物中相似性結構同區域測點關聯性角度詳細討論了漂移校正方案,針對渡槽工程存在的監測量漂移現象,提出了一種基于密度聚類算法的動態校正模型。
(1) DBSCAN算法對處理任意形狀的聚類問題有較好的適應性,特別是發現時間序列聚類簇,因而在校正過程中可以靈敏發現序列中的漂移區間。
(2) 該模型采用滑動窗口模式,依據DBSCAN算法判定窗口內漂移區間,以初始漂移點為基準校正漂移序列。伴隨窗口掃掠過的位置,監測序列逐漸被還原為漂移前的狀態。工程實例證明,該模型對于處理結構中存在多個相似測點的漂移問題有較高的校正精度。

