基于代價敏感神經網絡集成模型的類別不平衡問題研究

張俊杰, 曹 麗

(合肥工業大學 數學學院,安徽 合肥 230601)

類別不平衡問題是指數據集的各個類別的樣本數差異明顯,即某些類別的樣本數遠小于其他類別的樣本數。類別不平衡問題普遍存在于各個領域,如疾病檢查、軟件測試、病毒入侵、信用欺詐等。傳統的分類模型偏向對大類別樣本的學習而忽略小類別樣本的學習;但是在疾病診斷等領域,小類別樣本通常才是關注的重點,因此類別不平衡數據問題成為數據挖掘領域熱點問題之一。針對該問題,目前常用的解決方法主要集中在數據采樣、模型選擇和性能評估等方面。

在數據采樣方面,上采樣和下采樣是處理類別不平衡問題的常用方法。然而上采樣容易增加噪聲樣本的比例,導致模型出現過擬合;下采樣容易丟失重要樣本,導致模型出現欠擬合。因此文獻[1]對上采樣方法進行了改進,提出SMOTE方法,但是該方法容易產生噪聲樣本,影響模型的分類效果。

在模型選擇方面,解決類別不平衡問題常采用集成模型,如SMOTEBoost模型[2]。該模型在每次迭代過程中通過SMOTE方法合成新小類別樣本,改變樣本類別分布,以增加再迭代時模型對小類別樣本的學習次數。類似的集成模型還有RUSBoost模型[3]和CUSBoost模型[4]。但這些串行模型的訓練樣本選擇與前一輪模型的學習效果直接相關,并非獨立采樣,一旦當前模型的誤差小于閾值,則當前模型學習停止,容易導致早停,影響集成模型效果。還有學者從代價敏感的角度解決類別不平衡問題,解決方法大致可分為類依賴代價矩陣法和樣本依賴代價矩陣法。類依賴代價矩陣法主要有代價敏感神經網絡[5]、Hard-Ensemble模型[5]和Soft-Ensemble模型[5]。樣本依賴代價矩陣法主要有樣本依賴代價敏感學習決策樹算法[6]和樣本依賴代價敏感學習Adaboost算法[7]。

在性能評估方面,當大類別樣本量遠大于小類別樣本量時,例如當類別比例為1∶99時,若將全部樣本判定為大類別樣本,則準確率達到99%,但是此時的準確率已無參考意義和評估價值。因此,在類別不平衡問題中通常使用如下的性能評估標準:精準率P、召回率R、P-R曲線、F1值以及ROC曲線等。文獻[8]將P-R曲線和ROC曲線做對比,在數據類別不平衡的條件下,ROC曲線的性能評估優于P-R曲線,但ROC曲線不能很好反映誤分類代價情況。

針對上述問題,本文提出代價敏感神經網絡集成(cost-sensitive neural network ensemble,CSNN-Ensemble)模型。首先通過多次隨機下采樣方式,每個基學習器學習不同的訓練樣本,防止樣本丟失;其次考慮誤分類代價,用代價敏感神經網絡作為基學習器,實現更佳的分類效果;然后結合并行集成學習的思想,降低基學習器之間的關聯性;最后通過UCI上9組二分類數據集進行幾種集成模型的對比實驗,結果表明該模型具有一定的有效性和實用性。

1 代價敏感神經網絡原理

代價敏感學習是根據不同誤分類產生的不同代價,尋找使得模型的期望損失代價最小的機器學習方法;在代價敏感學習過程中,代價矩陣至關重要,決定著模型的分類結果。假設數據集共有n種類別,代價矩陣是由誤分類代價所構成的矩陣,用(Ci,j)n×n表示代價矩陣,其中Ci,j表示第i類誤分為第j類的代價。特別地,規定Ci,i=0。基于代價敏感原理,本文沿用文獻[9]給定的代價矩陣的3種類型:

類型1存在唯一的c,當j=c時,有Ci,j>h,并且對所有j≠i,Ci,j≠c=h;對j≠c和Cc=h,定義Ci=Ci,c。

類型2對所有j≠i,有Ci,j=hi≥1.0;定義Ci=hi。

3種類型中的Ci表示第i類代價。

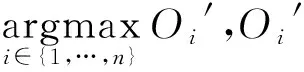
(1)

其中,η為歸一化參數。

2 代價敏感神經網絡集成模型原理

集成學習的基本思想是將多個獨立的、單一的基學習器按照某種結合策略有機地結合起來,從而獲得更準確的預測模型。目前主要的集成學習范式有提升(Boosting)和裝袋(Bagging)2種。Boosting集成范式采用串行模式,每輪訓練集的選擇與前一輪基學習器的學習效果相關,且基學習器以加權組合的方式構造集成模型。Bagging集成范式采用并行模式,各個基學習器之間獨立存在,模型相對簡單,能提高穩定性差的基學習器的預測精度。

本文采用Bagging集成范式構造代價敏感神經網絡集成模型。首先對原始數據集中大類別樣本N進行多次有放回的隨機下采樣,分別與小類別樣本M合并,構造m個訓練數據集;其次對每個訓練數據集分別訓練BP神經網絡,引入代價矩陣(Ci,j)n×n后,構造m個代價敏感神經網絡;最后對所構造出的m個代價敏感神經網絡進行并行組合。CSNN-Ensemble模型的算法流程如圖1所示,算法步驟如下:

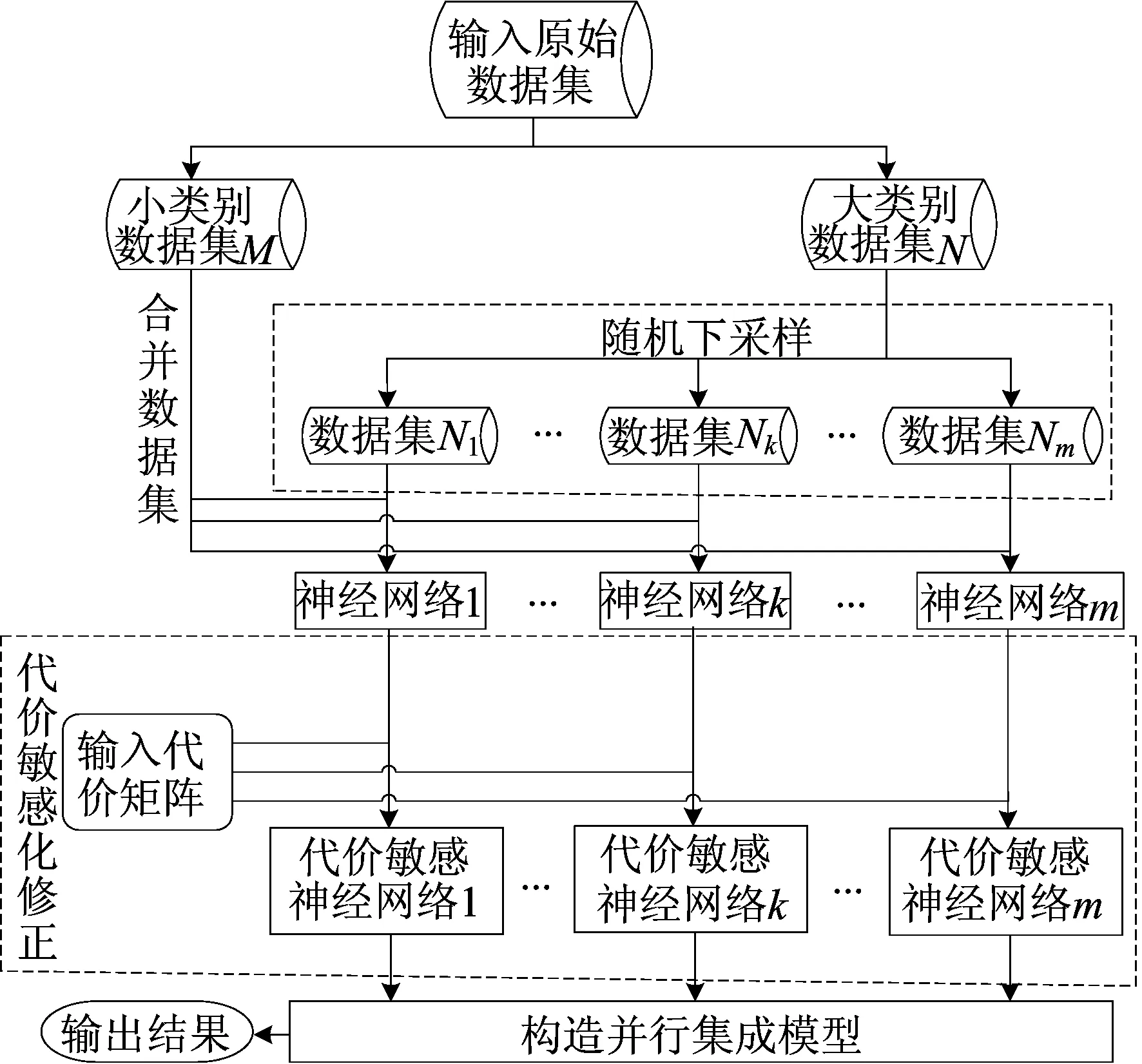
圖1 CSNN-Ensemble模型的算法流程

1) 輸入小類別樣本M、大類別樣本N、基學習器數量m以及代價矩陣(Ci,j)n×n;

2) 使用有放回的獨立隨機下采樣方法,從N中采樣得到m個樣本子集Nk,使Nk的樣本量與M的樣本量相等,且Nk?N,k=1,2,…,m;

3) 將m個下采樣子集Nk分別與M合并,訓練出m個神經網絡Hk;

4) 對每個Hk,分別引入代價矩陣,將其概率值與之相對應的誤分為其他類的代價相乘并求和,歸一化計算后得到代價敏感神經網絡Hk′;

CSNN-Ensemble模型以代價敏感神經網絡作為基學習器,模型相對簡單、復雜度低,且采用并行組合策略,能夠降低模型的方差,增加模型魯棒性。

3 實證分析

3.1 性能評估方法介紹

對于分類問題,分類準確率常常作為最重要的評價指標,但是在類別不平衡數據中,因為這種評價方法通常對大類別樣本偏袒嚴重,而忽略對小類別樣本的識別率,所以分類準確率對于類別不平衡數據往往不太合理。因此,本節將混淆矩陣介紹F1值、ROC曲線和代價曲線作為模型性能度量方法。混淆矩陣形式見表1所列。

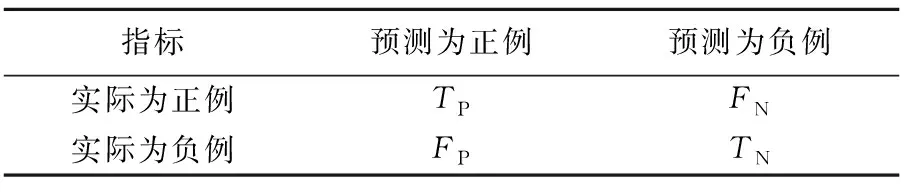
表1 混淆矩陣

精準率P、召回率R和假正例率RFP定義分別如下:

(2)

(3)

(4)

其中,召回率也稱為真正例率RTP。

F1值計算公式如下:

F1=2PR/(P+R)

(5)

ROC曲線是以假正例率RFP為橫坐標、真正例率RTP為縱坐標繪制而成。定義ROC曲線下方面積為AUC值,模型分類性能的優劣與AUC值的大小成正比。代價曲線是一種考慮了誤分類代價的分類性能度量方法;它是以正例概率代價PC(+)為橫軸,以歸一化代價NEC為縱軸繪制而成。PC(+)和NEC定義如下:

(6)

(7)

其中:P(+)、P(-)分別為樣本中正、負例的概率;C(-|+)為正例誤判為負例的代價;C(+|-)為負例誤判為正例的代價;假反例率RFN=1-RTP。根據式(6)、式(7),將歸一化代價化簡為:

NEC=(1-RFP-RTP)PC(+)+RFP

(8)

由式(8)可知,歸一化代價和正例概率代價是一種線性關系,且ROC曲線上的每個點(RFP,RTP)對應一條歸一化代價直線。連接歸一化代價直線的最小值點所形成的曲線即為代價曲線。定義代價曲線下方的面積為期望總體代價,模型分類性能的優劣與期望總體代價的大小成反比。

3.2 實驗結果分析

本文選出UCI數據集中9組二分類數據作測試驗證,數據信息見表2所列。

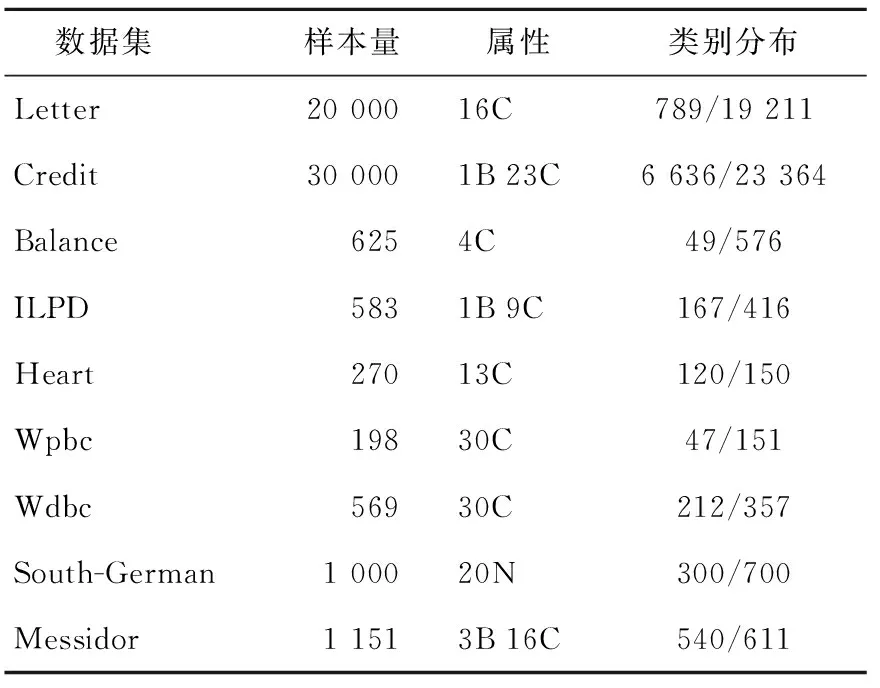
表2 數據集信息

有個別數據集中含有多種類別樣本,選擇其中一個樣本量少的類為小類別樣本,其余類別合并成大類別樣本。

在二分類問題中,3種代價矩陣類型沒有區別,且都可以用第3種類型進行表示[5],因此本文使用第3種類型代價矩陣訓練CSNN-Ensemble模型,對數據標準化處理后作為輸入數據進行模型驗證。

在9組數據集中,分別將GBDT模型、Random-Forest模型、Easy-Ensemble模型、Bagging模型、Adaboost模型與CSNN-Ensemble模型做對比,并采用10折交叉驗證方式驗證模型的有效性。

其中:Easy-Ensemble模型[10]的基學習器為Adaboost模型;Bagging模型的基學習器為BP神經網絡模型;Adaboost模型的基學習器為決策樹模型。通過對比6種模型的F1值、ROC曲線和代價曲線完成性能評估。6種模型的ROC曲線和代價曲線如圖2、圖3所示;F1值、AUC值和期望總體代價的10折交叉驗證結果見表3～表5所列。

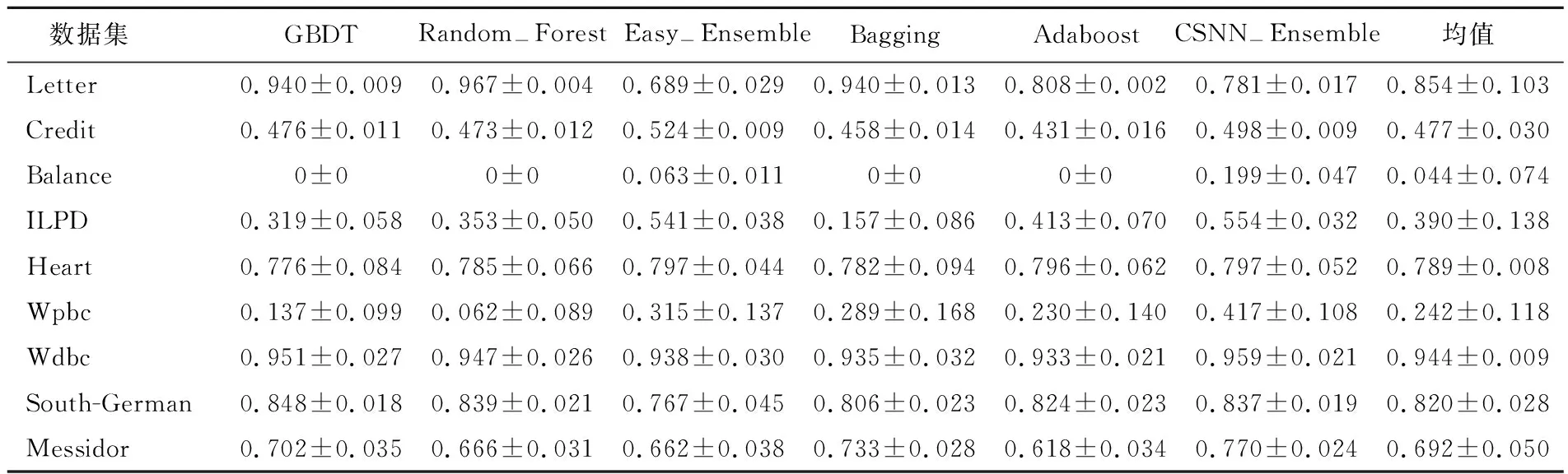
表3 6種模型在9組數據集中的F1值

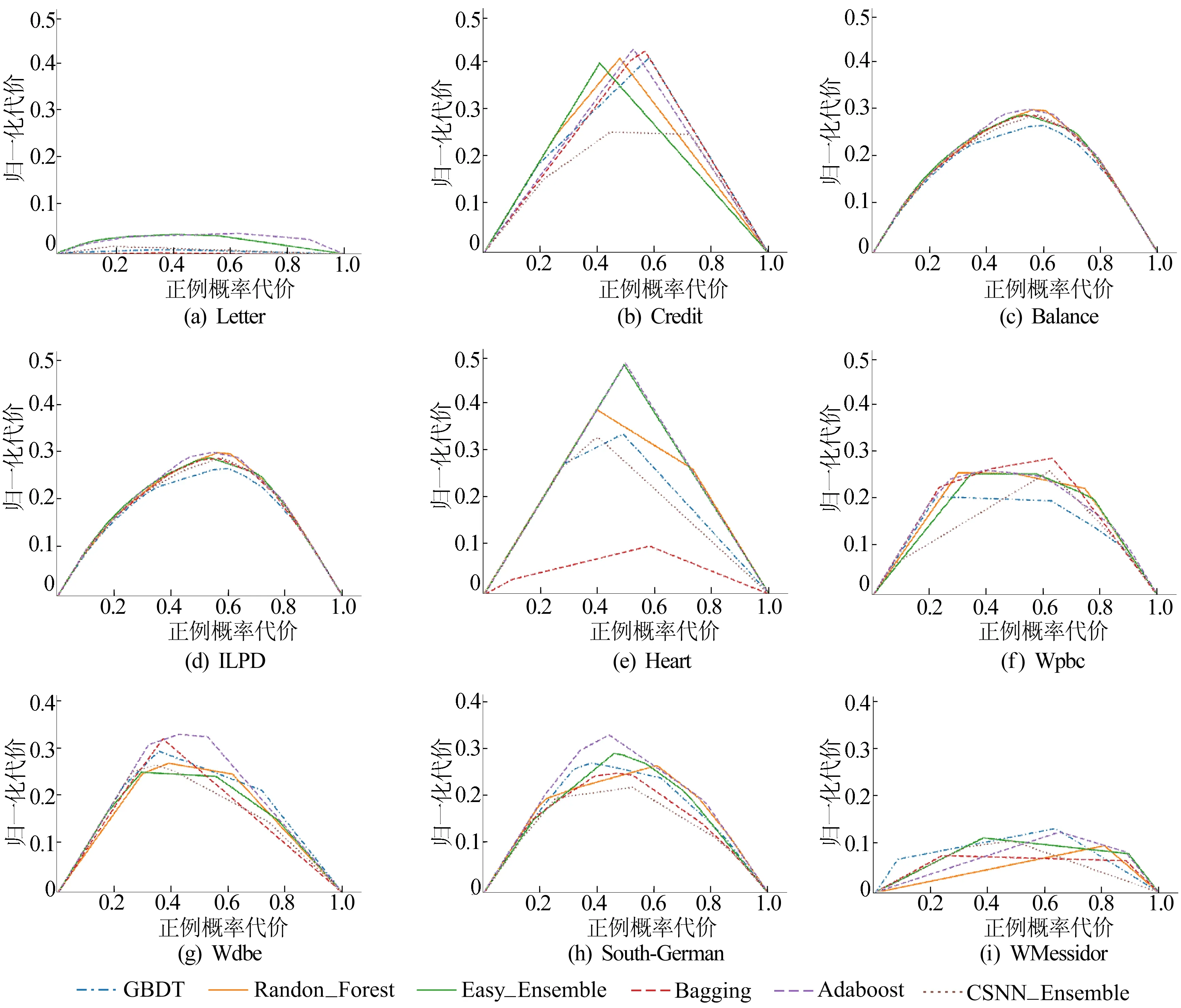
圖3 6種模型在9組數據集中的代價曲線

實證結果表明,在處理類別不平衡數據問題時,Adaboost模型在9組數據集中表現效果較差,而與之相比的其他5種模型都或多或少地表現出較強的分類性能。

F1值作為精準率和召回率的調和平均數,F1值越大,模型性能越優。從表3可以看出,在F1值的平均值大于0.8的數據集中,GBDT模型、Random-Forest模型、CSNN-Ensemble模型表現出相對較好的性能;而在F1值的平均值小于0.8的數據集中,Easy-Ensemble模型和CSNN-Ensemble模型的性能較優;這2種模型都是使用下采樣方法進行數據處理,因此下采樣處理類別不平衡問題是合理的。

從表4和表5可以看出,只有Balance數據集中6種集成模型結果相差較大,這可能是樣本特征屬性和樣本量較少的原因。在9組數據集中,僅CSNN-Ensemble模型的AUC值和期望總體代價優于平均值。究其原因不難發現,該模型在基學習器中引入代價因子后,改變了分類閾值,使模型對樣本的分類結果偏向于小類別樣本。

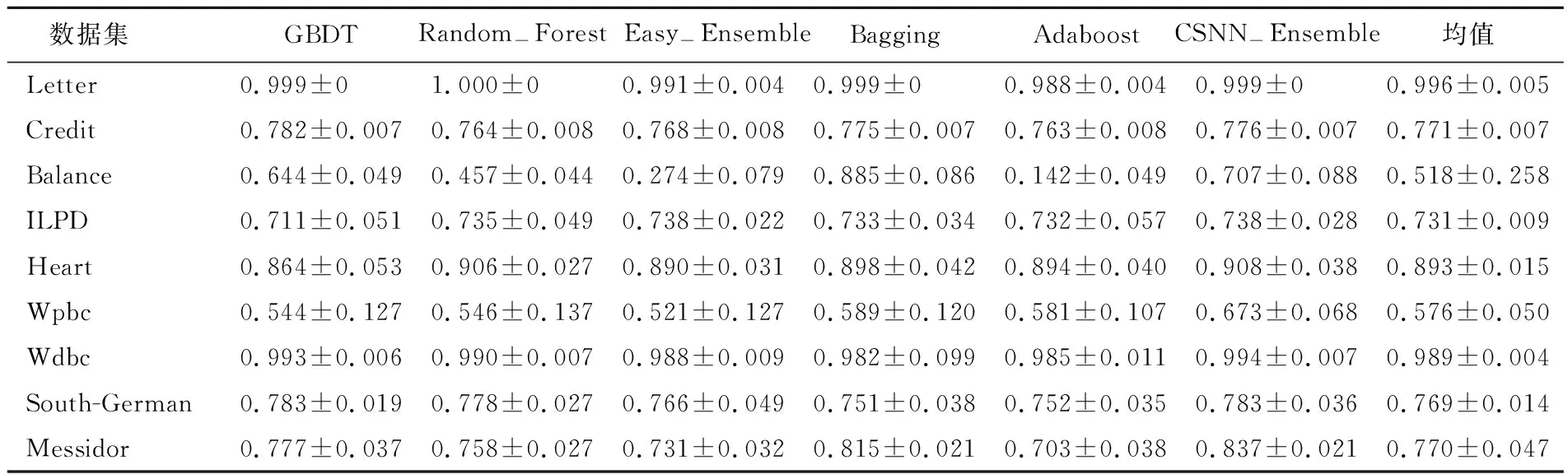
表4 6種模型在9組數據集中的AUC值

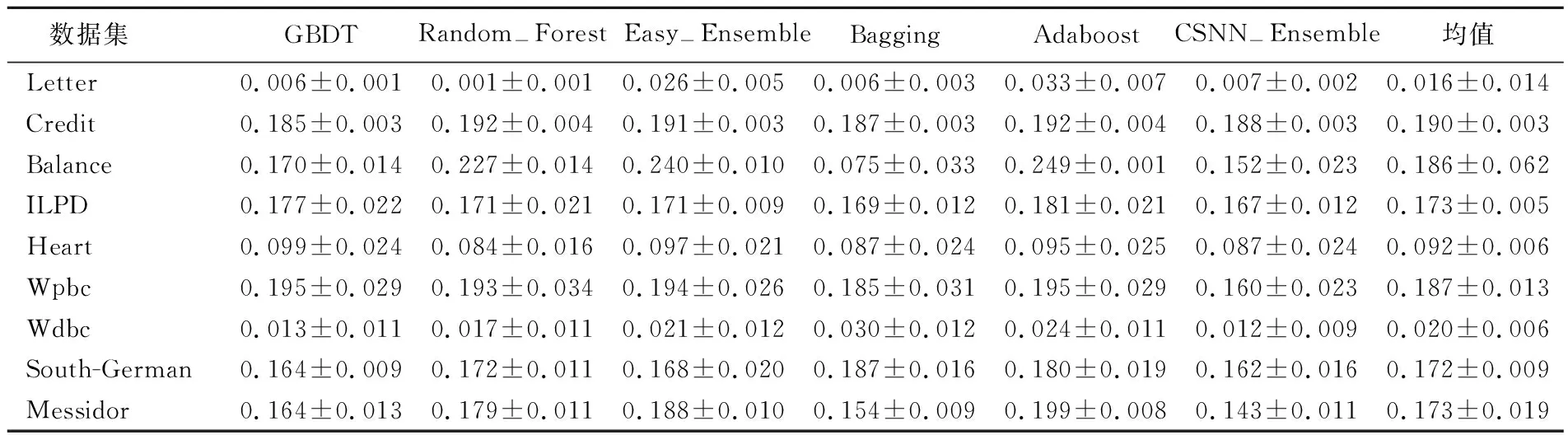
表5 6種模型在9組數據集中的期望總體代價

為了進一步從整體上評價模型優劣,對F1值、AUC值、期望總體代價3種性能結果采用Friedman檢驗,檢驗結果見表6所列。

從表6可以看出,CSNN-Ensemble模型均獲得了最低的平均序值。根據3種平均序值計算的Friedman檢驗值τF分別為2.532、4.857、6.098,均高于在顯著性水平α=0.05下的臨界值2.449,于是拒絕“所有模型性能相同”的假設;因此CSNN-Ensemble模型優于其他模型。

4 結 論

在類別不平衡數據問題研究中,針對下采樣方法導致的樣本丟失和分類過程中存在誤分類代價不等問題,本文結合代價敏感神經網絡與并行集成思想,構造了CSNN-Ensemble模型。首先通過多次隨機下采樣,每個基學習器能學習不同的訓練樣本,防止樣本丟失;然后在此基礎上,構造以代價敏感神經網絡為基學習器的并行集成模型,降低數據擾動對基學習器的影響。該模型以投票的方式進行決策,保證了所有基學習器的權重相同。實驗結果表明CSNN-Ensemble模型有效提高了分類性能。然而,如何對基學習器采用加權組合的方式構造集成模型將是下一步的研究方向。