具有間斷解的PTT型黏彈性流體熱對流數值模擬*

張欄， 蔣子超， 陳玉惠， 張儀， 楊耿超， 姚清河

1.中山大學航空航天學院，廣東 深圳 518107

2.Robotics and Mechatronics， University of Twente， Enschede 7522 NB， the Netherlands

熱對流是由溫度差驅動的流體運動，是自然界中普遍而重要的現象，廣泛存在于海洋、大氣、地核以及恒星和行星的內部。Rayleigh-Bénard（RB）熱對流是最常見、最典型的熱對流模型之一。近年來，國內外學者針對牛頓流體的RB 熱對流進行了廣泛研究（Bodenschatz et al.，2000；石峯等，2008；周全等，2012；賀嘯秋等，2022），但對黏彈性流體的RB 熱對流研究仍較少。事實上，研究黏彈性流體的RB 熱對流對于化學工業和地質研究都有重要意義（Hayat et al.，2008；Ogawa，2008）。相對牛頓流體而言，黏彈性流體包含了復雜的流變動力學特性，其實驗模擬和解析求解都存在較大困難。近年來，隨著計算機性能和計算流體力學數值方法的發展，黏彈性流體數值模擬的精度與分辨率都取得了突破性提升，對其進行直接數值模擬也逐漸成為了該領域重要的研究手段（Abu-Ramadan et al.，2003；Goswami et al.，2021；Kuron et al.，2021；Tseng，2021）。

黏彈性流體的本構模型選擇對于其仿真有著關鍵影響，當前被廣泛采用的本構模型主要有Oldroyd-B 模型（Oldroyd，1950；李勇等，2019）、FENE-P 模型（Bird et al.，1995）、Phan-Thien-Tanner（PTT）模型（Chen et al.，2021，2022）等。其中，PTT 模型由Phan-Thien 和Tanner 根據Lodge-Yamamoto 聚合物網絡理論推導得到（Thien et al.，1977；Phan-Thien，1978），相較于Oldroyd-B 模型，PTT本構模型更適合描述聚合物熔體和濃縮溶液的流變特性。通過調整模型材料參數，PTT模型可模擬多種高分子聚合物的流變性質（Quinzani et al.，

1994；Azaiez et al.，1996；Schoonen et al.，1998；Shin et al.，2007）。對于擠出脹大等黏彈性流體效應，基于PTT 模型的仿真結果具有較好的預測能力（Edeleva et al.，2021）。

近年來已有基于PTT 模型的黏彈性流體的熱對流及其他流動仿真，特別是低Rayleigh 數下RB熱對流的數值模擬研究。例如Park et al.（2004，2009，2018）使用基于逐格反演方法（grid-by-grid inversion method）的有限體積法，Zheng et al.（2022）使用基于高階迎風中心格式的有限差分法（FDM，finite difference method）均實現了PTT 型黏彈性流體RB 熱對流的數值模擬，對其流動特性進行了詳細探討。目前研究所采用的數值方法普遍難以處理間斷現象，需要考慮高數值穩定性的新型離散格式。

方程非線性項引發的間斷解問題一直是計算流體力學中的關鍵問題，圍繞方程非線性項的離散，已有許多重要研究方法，總變差不增（TVD，total variation diminishing）格式為其中的關鍵成果之一。TVD 格式最早由Harten（1983）提出并被應用于可壓縮流動的FDM 求解，由于其能夠準確地捕捉激波的位置、在高分辨率下仍可以維持對間斷解的數值穩定性，從而逐漸成為了主流離散格式。近年來TVD 格式被廣泛應用于磁流體動力學（Yuan，2019）、地熱儲層工程（Oldenburg et al.，2000）和潰壩水力學（劉玉玲等，2010）等領域內，在其基礎上構造的其他高精度無波動格式也取得了諸多應用成果（?ada et al.，2009；Kemm，2011；Dubey，2013）。但是，將TVD 格式應用于黏彈性流體RB對流數值模擬的研究仍較少。

從間斷解充分發展的黏彈性流體RB 熱對流具備不同流態的時間信息和發展過程的流態變換，研究該問題對闡明PTT 型黏彈性流體RB 熱對流的流動機理具有重要意義。為解決PTT 本構模型在RB 對流中可能會引起間斷和數值振蕩問題，本研究將基于TVD 離散格式和PTT 本構模型，開發一種黏彈性流體RB 熱對流FDM 模擬方法。該方法能夠應用間斷初始條件進行長時間模擬，并通過與穩定周期解的對比驗證其有效性。

1 數值模型及算法實現

1.1 控制方程

采取布辛涅司克近似模擬該對流問題，控制方程（Zheng et al.，2022）為

其中u，p，T，τ分別為黏彈性流體的速度、壓力、溫度和偏應力張量。基準溫度T0=(T1+T2)/2，T1為上邊界溫度，T2為下邊界溫度，ρ0為T=T0時黏彈性流體的密度。常數α為熱膨脹系數，g為重力加速度，k為熱傳導系數，Cp為比熱容，ej為重力加速度方向上的單位向量。

偏應力張量τ為二階對稱張量，通常可以分解為牛頓溶劑貢獻和聚合物貢獻

其中τs= 2μsD為黏性偏應力張量，μs為溶劑黏度，應變率張量D=.τp為彈性偏應力張量，對于PTT本構模型有

其中λ為弛豫時間，μp為聚合物黏度，?為分子應變率，ξ為分子滑移率。

將控制方程中各量進行無量綱化，

其中H為特征尺度，ΔT為最大（邊界）溫差，Uc=為特征速度，κ為熱擴散系數，ν為運動學黏度。

無量綱化的控制方程為

其中Ra=為瑞利數，We=κλ/H2為魏森貝格數，Pr=(μ0Cp)/k為普朗特數，均為黏彈性流體RB 熱對流問題中重要無量綱參數。β=μs/μ0為比黏度，即溶劑黏度與總黏度的比值，總黏度μ0=μs+μp，Ma=為馬赫數，表示橫波速度與流體特征速度的比值。

本文采用有限差分法對上述方程進行數值模擬，其中溫度場由顯格式求解，壓力場基于SIMPLE算法求解。

1.2 適用于間斷解的離散方法

首先將方程（2）～（3）分離源項擬線性化并轉化成守恒形式得到

其中W=[u，v，τ11，τ12，τ22]T，u和v分別為x和y方向上的速度分量，τij(i，j= 1，2)為彈性偏應力的應力分量，流通量矢量定義為

相應地，源項

應用局部特征方法，方程(5)可以表示為

其中雅可比矩陣

A2具有類似的形式。

時間上對時間的偏導數項采取一階向前差分格式離散，其他項均顯式處理。方程（1）～（4）在時間上的半離散格式為

空間上的離散采用均勻網格，使用二階中心差分格式離散黏性項、能量方程的擴散項，使用二階迎風TVD差分格式（Harten，1983）離散擬線性項

格式黏性函數Q(z)定義為

本文取ζ=[0.05，0.5].

定義

本文采用minmod函數作為限制器

其中

2 數值驗證

為了驗證本文的數值方法的離散精度與收斂性，本文將基于理論解析解對數值結果進行精度校驗，考慮具有額外源項f1，f2的控制方程

其中額外源項f1=[fu，fv，fτ11，fτ12，fτ22]T，f2=fT，且

可證明，在寬高比為1∶1的方腔內，方程(6)～(8)的解析解

其中ω=kπ/L，η=10-5.選取參數β= 0.2，We= 0.1，Ra= 1 480，Pr= 0.7，?= 0.1，ξ= 0.05，取時間步長Δt= 10-5，在不同空間步長Δx下，本文所采用的求解算法所得的數值解與式(9)的解析解間2 范數誤差（L2-error）如圖1所示。

圖1中，Δx選取了1/1 024 ～ 1/32間對數坐標上的等距點，其對應的2 范數誤差與Δx近似成冪函數關系，其指數約為1.71.由此論證了本文所采用的TVD格式在空間上的收斂性與近似2階精度。

3 結果分析

本文RB 熱對流幾何模型采用寬高比為2∶1 的充滿黏彈性流體的方腔（見圖2）。

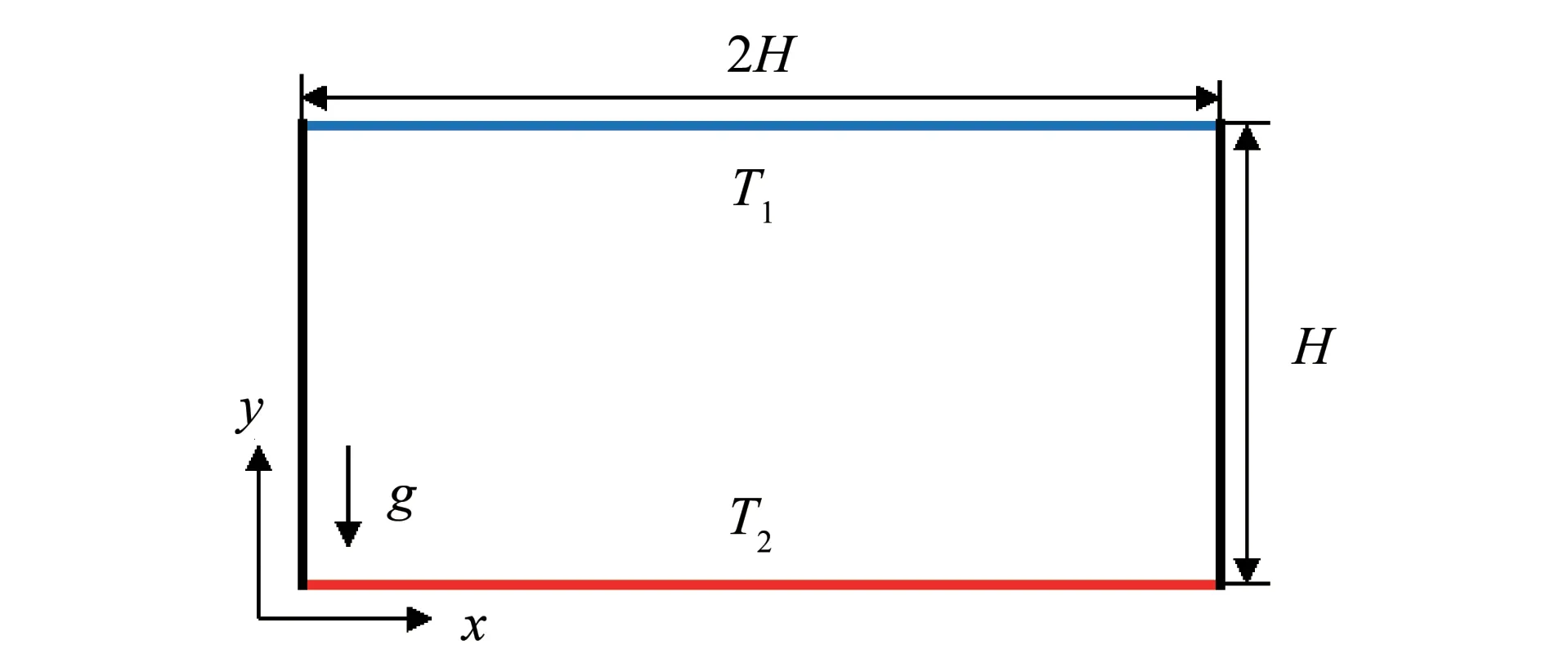
圖2 RB熱對流幾何模型與溫度邊界設置Fig.2 Geometric model of RB convection

無量綱化后該PTT 型黏彈性流體RB 熱對流的計算域為(x，y)：[0，2]×[0，1].速度邊界條件為四壁均為無滑移邊界條件；應力邊界條件為諾伊曼邊界條件；溫度邊界條件為上下壁面為等溫邊界條件，左右壁面為絕熱邊界條件，即

速度、應力初始條件均為0，初始溫度場為間斷場：上邊界和下邊界分別為0.5 和-0.5，除邊界外均為T0.

各個常數取值分別為β= 0.2，We= 0.1，Ra=1 480，Pr= 0.7，?= 0.1，ξ= 0.05.構建空間步長為1/64的均勻網格，取Δt= 10-3，對該模型進行時長550的數值模擬，其動能（Ek）發展如圖3所示。

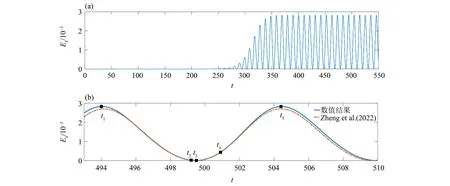
圖3 （a）全局動能隨時間的變化情況；（b）動能波動周期對比及單個周期內的5個代表性時間步（t1～t5）Fig.3 (a) Time evolution of global kinetic energy,（b） Comparison of kinetic energy fluctuation periods and five representative time steps （t1～t5）within a single period

由圖3 可見，PTT 黏彈性流體的RB 熱對流在充分發展后呈現出周期性流動的特性，動能隨著時間的波動周期為10.4，與Zheng et al.（2022）中由穩定周期解作為初始場的計算結果10.2 接近一致。由動能的量級估計，流動開始發展的時間為232.3且358.7 后達到穩定周期解。為進一步闡釋單周期內流動的性質，取相鄰動能最大值點內的5個代表性時間步，其溫度與速度場分布如圖4所示。

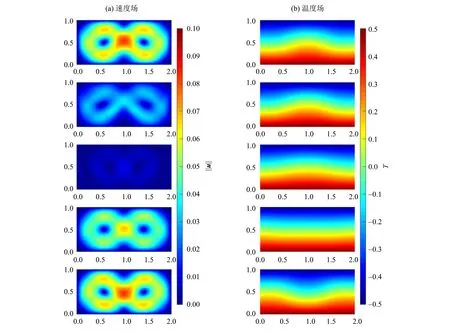
圖4 一個周期內的溫度場和速度場分布（由上至下分別對應t1，t2，t3，t4，t5）Fig.4 The distribution of velocity (a) and temperature (b) at the five time points(t1 to t5 from top to bottom) in one period

圖4 中，t1= 494，t5= 504.4 時，全局動能最大；t2= 499.2 時，方腔中心線底壁附近有新渦出現；t3= 499.5 時，全局動能最小；t4= 500.9 時，溫度場分布近似純熱傳導。由圖4（a）可見，在達到全局動能最大值(t=t1)后，流動沿著方腔中心線向上流動；至t=t2時，在方腔垂直中心線附近的底壁附近開始出現2 個小渦，然后迅速發展至t3時形成的四渦結構；時間在t3到t4之間渦逐漸合并，并在t4時再次過渡為兩渦結構。從方腔垂直中心線附近底壁出現小渦開始，流場的流向沿著方腔中心線向上流動，到t3時四渦結構形成，整個流場轉變到沿著方腔中心線向下流動。由圖4（b）可見，在t1到t3之間，溫度場基本沒有發生變化，但速度場卻在持續減弱，最大速度從t1的0.08 變化到t3的0.006。在t3～t4時間內，溫度場發生明顯變化。在t4時溫度分布幾乎可以近似在y方向上呈線性分布，接近于無對流的純熱傳導的穩態溫度分布。從t4到t5，全場速度逐漸增大并在t5處達到極值，溫度場也隨之偏離t=t3時的分布。

區別于牛頓流體，黏彈性流體熱對流除溫差驅動力外還存在著非均勻分布的內應力。在該數值模擬中，應力場的仿真結果如圖5所示。

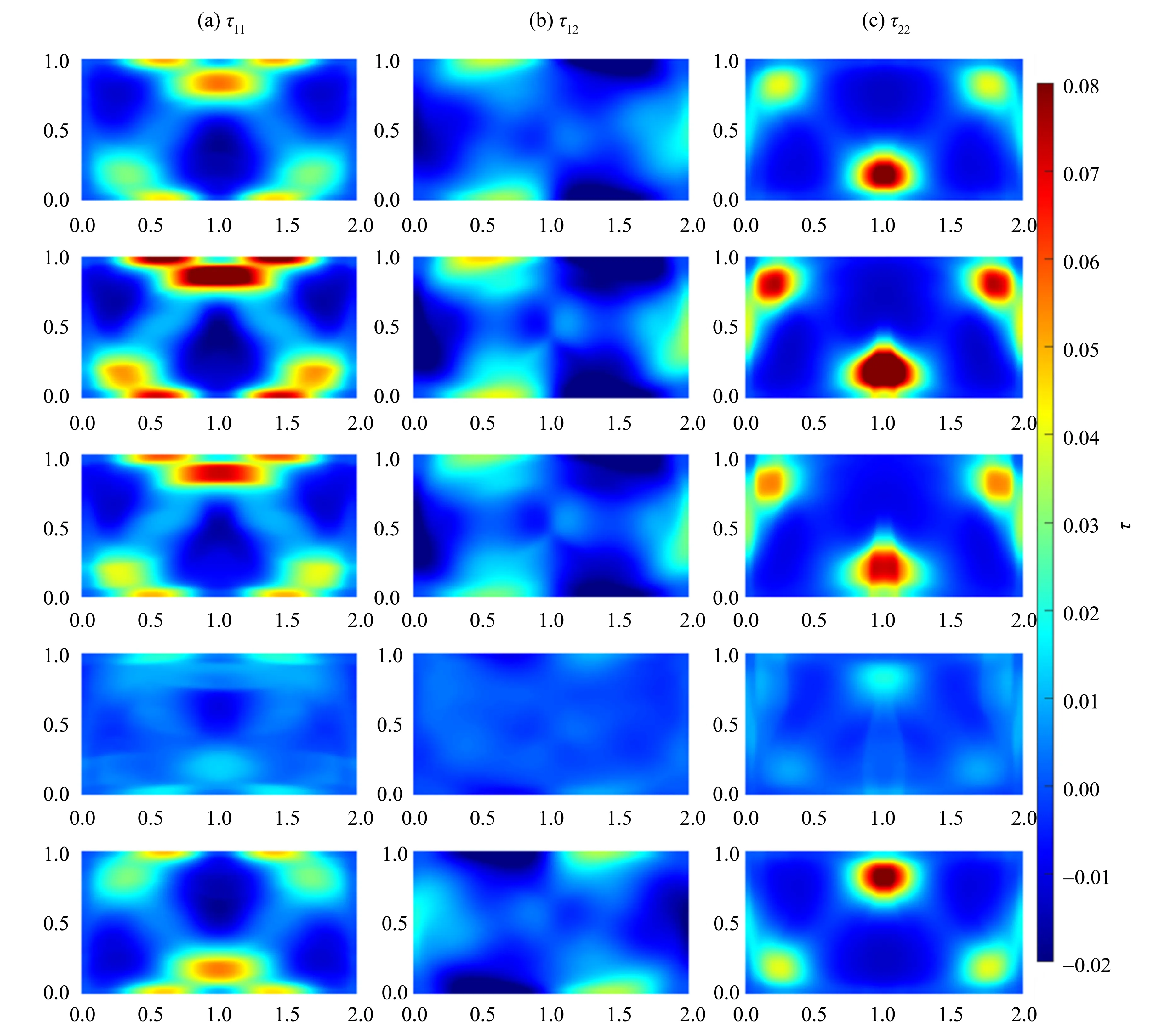
圖5 一個周期內的彈性偏應力場分布（由上至下分別對應t1，t2，t3，t4，t5）Fig.5 The distribution of extra-stress τ11, τ12 and τ22 at the five time points(t1 to t5 from top to bottom) in one period

由圖5 可知，在t=t1后，速度梯度極值不斷增大，同時彈性偏應力分量隨之增大。在t2時，τ11和τ22的最大值出現在(x，y) =(1，0.9) 和(x，y) =(1，0.3)附近，而從t1向t2的過程中，τij的散度增大，使得u和v由于?τ11/?x和?τ22/?y而增大。從t2到t3階段τij達到極大值后向減小開始變化，但減小的幅度很輕微；在t3到t4階段τij減小幅度很大，并于t4時τij達到極小值。此階段速度場的增大加劇了τij的衰減。從t3到t4階段，τ11和τ22的正負沿垂直中心線變化。在t3時，τ11在(x，y) =(1，0.9)處為正，在(x，y) =(1，0.3)處為負，而在t5時，τ11在相同位置改變正負，在(x，y) =(1，0.9)處為負，在(x，y) =(1，0.3)處為正。

在下一個全局動能周期，也是速度場的下半周期，速度梯度由零開始逐漸向極值增大，速度梯度的增大使τij增大，全局動能最小時在垂直中心線附近的頂壁附近出現小渦，迅速擴大并侵入腔體快速轉化成四渦結構，流動方向發生逆轉，溫度場的對流分布轉變為近似在y方向上呈線性分布；τij繼續衰減，τ11和τ22沿方腔垂直中心線變化，速度再次放大達到極值，溫度場再次變為對流分布。

上述流動現象表明，速度場的減弱-放大循環與彈性偏應力場的衰減-增大循環之間存在相位差，相位差的存在導致了PTT 型黏彈性流體RB 熱對流隨時間變化的流動狀態，并且在速度場的完整周期里出現反向對流現象。

4 結 論

本文采用了基于TVD 差分格式的FDM 模擬了基于PTT 型黏彈性流體的RB 熱對流問題，對非線性黏彈性流體在封閉方腔內部的對流過程進行了研究，得到如下結論：

1） 本文的數值結果與解析解與文獻相符，且具有二階空間精度。

2） 數值模擬結果表明，基于TVD 格式的求解方法能夠有效地模擬黏彈性流體RB 熱對流問題，并得到流動從間斷初始條件開始發展到穩定周期解的完整過程的瞬態信息。

3） PTT 型黏彈性流體RB 熱對流的基本流動現象顯示，在充分發展后會呈現出隨時間變化的振蕩對流特征，并具有特定流動模式以及流動反轉的流動特性。