基于模糊神經網絡控制方法的光伏發電系統并網設計

陳宇能，陳景賢，廖鈞濠，陳秀雯

摘 要：針對光伏發電系統運行過程中極易受到環境溫度、太陽輻照度等外部條件干擾，從而導致其輸出功率存在間歇性、隨機性問題的情況，提出一種基于模糊控制算法及前饋（BP）神經網絡的智能控制方法（下文簡稱為“模糊神經網絡控制方法”）來進行光伏發電系統并網設計，并搭建并網電路模型進行仿真分析。分析結果顯示：相較于擾動觀察法、模糊控制算法，采用模糊神經網絡控制方法的并網光伏發電系統的泛化能力和魯棒性更強，能更好地提高系統的穩態性和可靠性，可有效解決光伏發電輸出功率存在的間歇性和隨機性問題。

關鍵詞：光伏發電系統；最大功率點追蹤；神經網絡；模糊控制算法；并網

中圖分類號：TM615 文獻標志碼：A

0? 引言

隨著化石能源過度消耗，環境污染問題日趨嚴重，開發利用清潔、高效的可再生能源已成為世界各國能源發展的必然趨勢[1]。太陽能是一種無噪聲、無污染、資源分布不受地域限制的可再生能源，而光伏發電被認為是最有發展前景的太陽能利用方式之一。雖然利用微電網將光伏電力接入配電網能提高配電網的輸配電容量[2-3]，但卻無法完全解決光伏發電系統輸出功率存在波動性、不穩定的問題[4] 。此外，當光伏發電系統受到外部環境干擾而導致其輸出電壓產生波動時，其并網后電網也會受到相應的擾動，進入“孤島”運行模式[5]。

目前，國內外關于優化光伏發電系統輸出功率分配的研究主要是采用逆變器結合相應的控制手段來提高光伏發電系統并網時的電能質量。比如：文獻[6]提出使用動態恒定電壓法實時跟蹤光伏發電系統的最大功率點（MPP）電壓，但該方法需要具備高精度的環境溫度、太陽輻照度傳感器，增大了硬件成本；文獻[7]通過采用擾動觀察法對光伏發電系統進行擾動，以改變占空比，從而實現最大功率點追蹤，但在最大功率點處仍存在波動；文獻[8]提出以粒子群優化（PSO）模糊控制算法追蹤光伏發電系統的最大功率點，雖然該方法全局搜索能力強、準確性較高，但易陷入局部最優。

上述文獻均是通過光伏發電系統輸出特性曲線來追蹤最大功率點，并通過算法提高追蹤精度，但仍難以解決光伏發電輸出的間歇性和隨機性問題。本文提出一種基于模糊控制算法及前饋（BP）神經網絡的智能控制方法（下文簡稱為“模糊神經網絡控制方法”）來進行光伏發電系統并網設計，該方法利用多層BP神經網絡強大的推理能力，直接預測出光伏發電系統最大功率點電壓；再通過模糊控制算法，利用專家經驗，實時調整占空比，推算出光伏發電系統最大功率點，從而提高系統的泛化能力和魯棒性，進而有效抑制光伏發電系統輸出的間歇性和隨機性，為并網光伏發電系統的安全運行提供保障。

1? 模型的搭建

1.1? 光伏組件的等效電路模型

光伏組件是利用光生伏特效應將太陽能轉變為電能的裝置。典型的光伏組件等效電路模型可看作是一個受控電流源[9]，具體如圖1所示。圖中：Rs和Rp分別為光伏組件的等效串聯電阻和等效并聯電阻；Is和Ip分別為流經光伏組件等效串聯電阻和等效并聯電阻的電流；Ipc為光生電流；Id為流經二極管的電流；Ipo為光伏組件的輸出電流；Vpo為光伏組件的輸出電壓；D為二極管。

根據基爾霍夫電壓定律（KVL）可知，流經光伏組件等效并聯電阻的電流可表示為：

（1）

流經二極管的電流可表示為：

（2）

式中：Io為光伏組件的反向飽和電流；q為電荷量常數；Vpv為二極管兩端的電壓；nc為二極管理想因子；k為玻爾茲曼常數；Tc為光伏組件工作溫度。

根據基爾霍夫電流定律（KCL）可知，光伏組件的輸出電流可表示為：

Ipo=Is=Ipc–Id–Ip? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（3）

將式（1）和式（2）代入式（3），則可得到光伏發電的輸出特性方程，即：

（4）

1.2? 光伏陣列輸出特性

由于單塊光伏組件的輸出電流過小、輸出功率過低，難以實現與市電并網。因此由多塊光伏組件按拓撲結構相互連接構成光伏陣列，并將其作為光伏發電的研究對象。單塊光伏組件的工作參數如表1所示。

太陽輻照度和環境溫度的變化都會對光伏陣列的輸出特性造成影響。針對同一個光伏陣列，通過改變這兩個因素，研究不同環境溫度和不同太陽輻照度下光伏陣列的輸出特性。

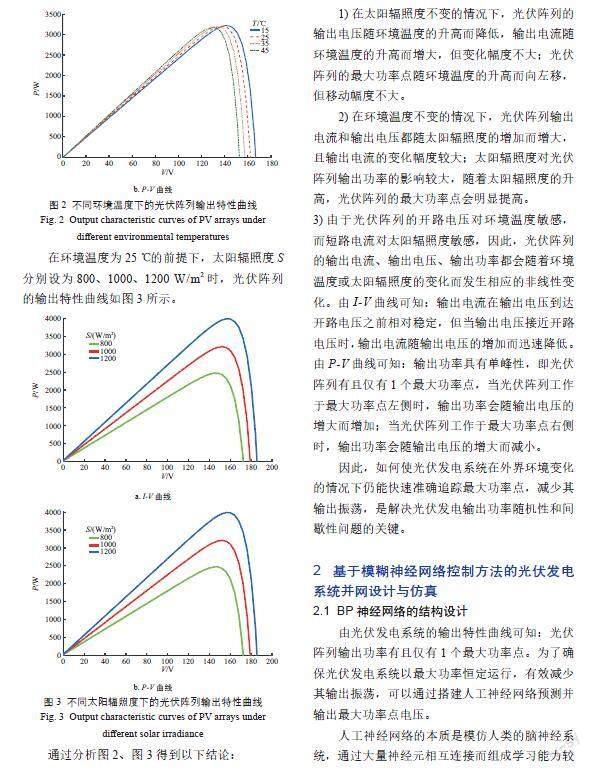
在太陽輻照度為1000 W/m2的前提下，環境溫度T分別設為15、25、35、45 ℃時，光伏陣列的輸出特性曲線如圖2所示。圖中：I為光伏陣列的輸出電流；V為光伏陣列的輸出電壓；P為光伏陣列的輸出功率。

在環境溫度為25 ℃的前提下，太陽輻照度S分別設為800、1000、1200 W/m2時，光伏陣列的輸出特性曲線如圖3所示。

通過分析圖2、圖3得到以下結論：

1）在太陽輻照度不變的情況下，光伏陣列的輸出電壓隨環境溫度的升高而降低，輸出電流隨環境溫度的升高而增大，但變化幅度不大；光伏陣列的最大功率點隨環境溫度的升高而向左移，但移動幅度不大。

2）在環境溫度不變的情況下，光伏陣列輸出電流和輸出電壓都隨太陽輻照度的增加而增大，且輸出電流的變化幅度較大；太陽輻照度對光伏陣列輸出功率的影響較大，隨著太陽輻照度的升高，光伏陣列的最大功率點會明顯提高。

3）由于光伏陣列的開路電壓對環境溫度敏感，而短路電流對太陽輻照度敏感，因此，光伏陣列的輸出電流、輸出電壓、輸出功率都會隨著環境溫度或太陽輻照度的變化而發生相應的非線性變化。由I-V曲線可知：輸出電流在輸出電壓到達開路電壓之前相對穩定，但當輸出電壓接近開路電壓時，輸出電流隨輸出電壓的增加而迅速降低。由P-V曲線可知：輸出功率具有單峰性，即光伏陣列有且僅有1個最大功率點，當光伏陣列工作于最大功率點左側時，輸出功率會隨輸出電壓的增大而增加；當光伏陣列工作于最大功率點右側時，輸出功率會隨輸出電壓的增大而減小。

因此，如何使光伏發電系統在外界環境變化的情況下仍能快速準確追蹤最大功率點，減少其輸出振蕩，是解決光伏發電輸出功率隨機性和間歇性問題的關鍵。

2? 基于模糊神經網絡控制方法的光伏發電系統并網設計與仿真

2.1? BP神經網絡的結構設計

由光伏發電系統的輸出特性曲線可知：光伏陣列輸出功率有且僅有1個最大功率點。為了確保光伏發電系統以最大功率恒定運行，有效減少其輸出振蕩，可以通過搭建人工神經網絡預測并輸出最大功率點電壓。

人工神經網絡的本質是模仿人類的腦神經系統，通過大量神經元相互連接而組成學習能力較強的運算模型。由這些神經元所搭建的網絡理論上可以向任意的已知函數學習[10]。本文采用BP神經網絡，其利用誤差反向傳播訓練算法，基本原理是梯度下降法，即通過調整權值使神經網絡的實際輸出值與期望輸出值之間誤差的均方根值最小[11]。BP神經網絡結構圖如圖4所示。圖中：太陽輻照度和環境溫度均為輸入信號；參考輸出電壓Vref為輸出信號；wij為連接輸入層與隱含層之間的權值；wki為連接隱含層與輸出層之間的權值。

將輸入的環境溫度、太陽輻照度數據進行歸一化處理，歸一化區間為[0，1]。以歸一化后的數據作為BP神經網絡的二維輸入向量，將隱含層神經元個數設置為7，輸出層神經元個數設置為1，數據采樣的間隔為0.01，設定目標誤差為0.0001，學習速率設定為0.01；并用S型正切函數tansig作為隱含層神經元的傳遞函數，以S型對數函數logsig作為輸出層神經元的傳遞函數，以trainlm函數進行BP神經網絡訓練。

以某個光伏陣列為例，將其最大功率點下的實際輸出電壓與BP神經網絡預測的參考輸出電壓進行對比，對比結果如圖5所示。

由圖5可知：所采用的BP神經網絡可在未知光伏陣列相關電氣參數的條件下，通過搭建相關模型，將輸入的環境溫度、太陽輻照度數據歸一化、訓練、測試，可以較準確地預測最大功率點下的參考輸出電壓，且神經網絡的逼近效果較高，訓練誤差較小，泛化能力較好，適用于非線性系統。

由此可見，利用BP神經網絡來追蹤光伏發電系統最大功率點具有很大優勢，能夠抑制光伏發電系統輸出電壓的不穩定性，有效解決輸出功率的間歇性和隨機性問題。

2.2? 模糊控制算法跟蹤光伏陣列最大功率點

以BP神經網絡預測的參考輸出電壓與光伏陣列實際輸出電壓的偏差E和偏差的變化量EC作為模糊控制算法的輸入信號，判斷光伏陣列輸出功率點與最大功率點之間的位置關系，通過調節作為輸出信號的占空比，使輸出電壓值趨向峰值電壓。將BP神經網絡預測的參考輸出電壓與實際輸出電壓偏差及偏差變化量的模糊子集設為{NB， NM， NS， ZO， PS， PM， PB}，論域為{-1， 1}。其中：NB、NM、NS、ZO、PS、PM、PB分別為論域中的負大、負中、負小、零、正小、正中、正大。同時均選用含有中等模糊狀態定義的三角形作為隸屬函數。

第K次采樣下BP神經網絡預測的參考輸出電壓Vref（K）和光伏陣列實際輸出電壓V（K）的偏差E（K）及偏差變化量EC（K）可分別表示為：

E（K）=V（K）–Vref（K）? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （5）

EC（K）=E（K）–E（K–1）? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （6）

根據光伏陣列的P-V特性曲線制定4條模糊控制規則，分別為：

1）當EC（K）>0、E（K）>0時，輸出功率點在最大功率點左側，且逐漸遠離最大功率點；

2）當EC（K）>0、E（K）<0時，輸出功率點在最大功率點右側，且逐漸靠近最大功率點；

3）當EC（K）<0、E（K）>0時，輸出功率點在最大功率點左側，且逐漸靠近最大功率點；

4）當EC（K）<0、E（K）<0時，輸出功率點在最大功率點右側，且逐漸遠離最大功率點。

確定模糊控制規則后，可得到輸出功率變化時的占空比，并可制定出相應的模糊控制規則表，具體如表2所示。

在不影響跟蹤速度的前提下，將清晰化的最大功率點電壓與三角波進行調制，采用MAX-MIN推理方法調控步長。步長大小隨輸出功率點與最大功率點的距離自動調整，方向與輸出功率增加的方向相同。通過調節開關管的占空比進而改變光伏陣列的輸出電壓，跟蹤最大功率點，實現最大功率輸出。

2.3? 光伏輸出的仿真與分析

神經網絡通過學習、訓練得到的自適應樣本數據，可直接預測出最大功率點電壓，其具有非線性適應性信息處理能力，但需大量數據才能提高神經網絡的泛化能力；而且通常情況下，神經網絡欠缺規則表達能力且會出現過擬合現象。而模糊控制算法易于利用專家經驗，能夠表達和處理難以求取的信息，但模糊規則的提取缺乏學習能力[12]。由此可見，神經網絡和模糊控制算法具有互補特性。因此，可采用神經網絡和模糊控制算法相結合的方式跟蹤光伏發電系統的最大功率點電壓。

采用模糊神經網絡控制方法的并網光伏發電系統示意圖如圖6所示，圖中：L為Boost升壓電路的電感；De為Boost升壓電路的二極管；Co為輸出的濾波電容；Cpv為輸入的濾波電容；O為功率開關管。

該控制方法的工作原理為：首先將環境溫度和太陽輻照度的相關數據輸入到BP 神經網絡中，歸一化后訓練測試數據，通過調整BP神經網絡權值使光伏陣列的輸出電壓不斷逼近期望的最大功率點電壓；將BP神經網絡預測的參考輸出電壓與光伏陣列實際輸出電壓的偏差輸入到模糊控制器中，再通過模糊邏輯算法實時調節占空比，追蹤最大功率點，并通過并網模型將光伏發電系統的電力輸送到電網中，供電網調度。

假設光伏發電系統處于標準測試條件（太陽輻照度為1000 W/m2、環境溫度為25℃、AM1.5）下，不考慮光伏組件陰影遮擋問題，且光伏發電系統的最大功率為3200 W，為了驗證最大功率點追蹤（MPPT）算法的正確性，在光伏發電系統運行時間t為0.3 s時將太陽輻照度由1000 W/m2突變為800 W/m2，環境溫度保持不變，仿真時采用變步長ode23tb算法，對比擾動觀察法、模糊控制算法、模糊神經網絡控制方法的跟蹤效果，具體如圖7所示。

由圖7可以看出：3種方法均可跟蹤最大功率點。擾動觀察法的跟蹤效果一般，在0.08 s后才趨于穩定，且其對于太陽輻照度的突變，重新跟蹤的速度較慢，響應時間較長，振幅較大，存在最大功率點振蕩和誤判等缺點。相較于擾動觀察法，模糊控制算法的波形更加平滑，穩態時的振蕩更輕微，且輸出功率在0.05 s后基本穩定；同時，該方法跟蹤到的光伏發電系統最大功率約為2943 W，跟蹤性能參數Km=2943 W/3200 W=0.919，跟蹤性能較好。在t=0.3 s后，模糊控制算法能夠快速進行重新跟蹤，動態過渡時間和響應時間都較短。由此可見，模糊控制算法能使光伏發電系統輸出功率波形得到明顯改善，有效降低輸出的不穩定性。

相比于擾動觀察法和模糊控制算法，采用模糊神經網絡控制方法的光伏發電系統的輸出功率在0.03 s基本穩定，達到最大功率點后基本無振蕩，最大功率約為3038 W，跟蹤性能參數為0.949，跟蹤性能最好，穩態性能也更好；且在t=0.3 s時的擾動作用下能快速準確判定最大功率點走向，抗干擾能力強，無誤判現象。由此可知，BP神經網絡與模糊控制相結合，能更好學習與推理，快速預測和追蹤最大功率，更好解決光伏發電輸出的間歇性和隨機性，提高光伏發電系統穩定性。

3? 光伏發電系統并網分析

為了將光伏發電系統的輸出功率安全送到電網，供電網調度，需通過逆變器進行控制，以便于與市電同步，滿足并網條件。逆變器根據直流側電源性質可以分為兩大類：電流型逆變器和電壓型逆變器。由于電流型逆變器需在輸出側串聯大電感，以穩定輸入電流，考慮到實際裝置的體積和電路動態過程，最后采用電壓型逆變器，搭建全橋逆變型電路，并采用LCL型濾波器和電流滯環比較器。

LCL型濾波器雖然可以抑制高頻段信號，但高頻諧波分量被放大，若諧波直接流入電網，不利于電網的安全運行。為了改變LCL型濾波器的幅頻特性，減少輸出畸變，抑制諧振，故在LCL型濾波器電容中串聯阻尼電阻[13]。本文搭建的并網電路模型如圖8所示。圖中：i、iref分別為光伏發電系統的輸出電流和參考輸出電流；L1、L2均為電感；C為電容；R為電阻。

為了減少諧波分量，提高逆變器的電流輸出精度，電流滯環比較器1和電流滯環比較器2的滯環寬度分別為-0.65～0.70 A和-0.70～0.65 A，且留有“死區時間”，避免逆變橋直通。本文搭建的并網電路模型的相關參數如表3所示。

考慮到光伏發電系統的實際并網情況，逆變器與電網之間應接入變比為1：2的工頻隔離變壓器，以保護直流回路，避免諧波流入電網[14]。為測試電流滯環比較器的跟蹤效果，在工作頻率為50 Hz的情況下，對并網光伏發電系統進行運行仿真，得到給定電流和跟蹤電流的波形圖，如圖9所示。

從圖9可看出：給定電流的幅值為20 A，跟蹤電流從0. 02 s后與給定電流的幅值和相位基本保持一致。

從0.05～0.35 s時間段內的跟蹤電流中選取15個周波進行傅里葉變換，得到電流滯環比較器跟蹤電流的諧波分量和不含基波的諧波分量，結果如圖10所示。

從圖10可看出：電流滯環比較器跟蹤電流的諧波分量幅值為19.91 A，十分接近20 A，可近似看成其占給定電流的比例接近100%；不含基波的

諧波分量占比基本為零；總諧波失真為3.26%，符合電氣與電子工程師協會（IEEE）對并網光伏發電系統輸出電流總諧波失真不超過5%的要求。除去基波的諧波分量后，偶次諧波分量占跟蹤電流諧波的比例較小，可忽略不計；電流諧波含量最高的是三次諧波，所占比例不到0.1%，五次諧波分量所占的比例不到0.03%，且高次諧波總占比不到0.05%。由此可看出：并網光伏發電系統的運行效果較好，采用模糊神經網絡控制方法能有效改善諧波輸出，提高電能質量，避免諧波直接入網，從而提高電網運行效率。

4? 結論

本文提出了一種基于模糊神經網絡控制方法來進行光伏發電系統并網設計的方法，并利用該方法對并網光伏發電系統進行了仿真分析。分析結果顯示：相較于擾動觀察法、模糊控制算法，采用模糊神經網絡控制方法的并網光伏發電系統的泛化能力和魯棒性更強，能更好地提高系統穩態性和可靠性，有效解決了光伏發電輸出功率存在的間歇性和隨機性問題。此外，采用雙電流滯環比較器后，并網光伏發電系統輸出電流的高次諧波分量小，電流滯環比較器的跟蹤精度較高，更有效提高了電能質量和保障了電網的安全運行。

[參考文獻]

[1] 李凡雙，王展旭. 基于Cuk電路的光伏MPPT模糊控制系統仿真研究[J]. 自動化與儀器儀表，2019（4）：103-105，109.

[2] 張耀月.并網模式下的風光混合微電網中可再生分布式電源的建模與仿真[J].科技經濟導刊，2018，26（35）：34-42.

[3] MISHRA S，BORDIN C，TOMASGARD A，et al. A multi-agent system approach for optimal microgrid expansion planning under uncertainty[J]. International journal of electrical power & energy systems，2019，109：696-709.

[4] MAGDY G，SHABIB G，ELBASET A A，et al. Renewable power systems dynamic security using a new coordination of frequency control strategy based on virtual synchronous generator and digital frequency protection[J]. International journal of electrical power & energy systems，2019，109：351-368.

[5] 朱然，孫冀. 國外智能電網技術發展實踐綜述[J]. 電子質量，2016（9）：24-29.

[6] 倪雨. 基于阻增量光伏動態模型的高精度恒壓法設計[J]. 成都信息工程大學學報，2016，31（3）：297-300.

[7] 艾永樂，劉群峰，韓朝陽，等. 基于改進擾動觀察法的光伏MPPT策略[J]. 武漢大學學報（工學版），2020，53（4）：339-344.

[8] 徐偲吉吉，查曉銳.基于改進粒子群優化模糊控制的MPPT算法研究[J].電機與控制應用，2019，46（10）：35-39.

[9] BAI W L，LEE K. Distributed generation system control strategies in microgrid operation[J]. IFAC proceedings volumes，2014，47（3）：11938-11943.

[10] 酈丁浩. 基于人工神經網絡的MPPT算法研究[D]. 杭州： 浙江工業大學，2018.

[11] 蘇海濱，卞晶晶，劉強，等. 基于神經網絡的光伏發電最大功率點跟蹤算法[J]. 華北水利水電學院學報，2010，31（6）：80-83.

[12] 焦科名，徐凱. 基于神經網絡和模糊控制的光伏發電MPPT研究[J]. 計算機仿真，2020，37（5）：71-76.

[13] GOMES C C，CUPERTINO A F，PEREIRA H A. Damping techniques for grid-connected voltage source converters based on LCL filter：an overview[J]. Renewable and sustainable energy reviews，2018，81：116-135.

[14] 李建華. 光伏發電系統并網控制策略研究[D]. 蘭州：蘭州理工大學，2018.

Grid connection design of PV power generation system based on fuzzy neural network control method

Chen Yuneng1，Chen Jingxian1，Liao junhao1，Chen xiuwen2

（1. College of electronics and information engineering，Guangdong Ocean University，Zhanjiang 524088，China；

2. School of management，Guangdong Nanfang Institute of Technology，Jiangmen 529000，China）

Abstract：In response to the fact that PV power generation systems are highly susceptible to external conditions such as environmental temperature and solar irradiance during operation，resulting in intermittent and random issues with its output power，this paper proposes an intelligent control method based on fuzzy control algorithm and BP neural network （hereinafter referred to as“fuzzy neural network control method”） for grid connection design of PV power generation systems，and builds a grid connection circuit model for simulation analysis. The analysis results show that compared to the disturbance observation method and fuzzy control algorithm，the fuzzy neural network control method used in the grid connected PV power generation system has stronger generalization ability and robustness，which can better improve the steady-state and reliability of the system，and effectively solve the intermittent and random problems in the output power of PV power generation.

Keywords：PV power generation system；MPPT；neural network；fuzzy control algorithm；grid connection