基于阿波羅尼斯圓的應用

詹建峰

(深圳市華僑城高級中學,廣東 深圳 518053)

古希臘數學家阿波羅尼斯, 他證明過這樣一個命題:平面內與兩定點距離的比為常數的點的軌跡是圓.后人將這個圓稱為阿波羅尼斯圓,簡稱阿氏圓.近幾年,以阿氏圓為背景的考題不僅在高考中屢次出現,各地模擬試題中也頻繁出現,文章將對此作詳細分析.

1 阿氏圓定義的證明及性質

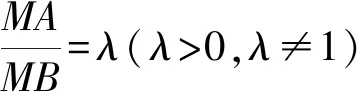
解析設定線段AB的長為2a,以線段AB所在直線為x軸,線段AB的中垂線為y軸,建立直角坐標系,則A(-a,0),B(a,0),M(x,y).

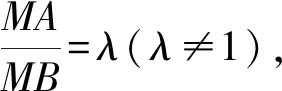
化簡得(1-λ2)x2+(1-λ2)y2+2a(1+λ2)x+a2(1-λ2)=0.

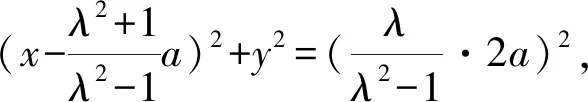
由上面的推導可以發現下列性質:

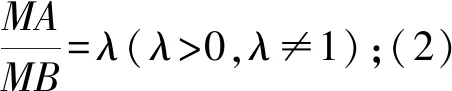
2 基于阿氏圓的題型分類

阿氏圓問題可以拆解成:(1)定點A、定點B; (2)定比λ; (3)定圓C.因此可以將阿氏圓有關的題型分解成以下幾種類型

類型1已知定點A、定點B和定比λ,求定圓C.

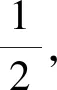
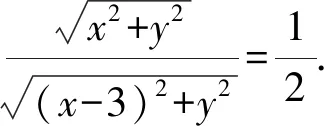
整理得到x2+y2+2x-3=0.

即(x+1)2+y2=4,是以(-1,0)為圓心,半徑為2的圓.

類型2 已知定點A、定點B和定圓C,求定比λ.

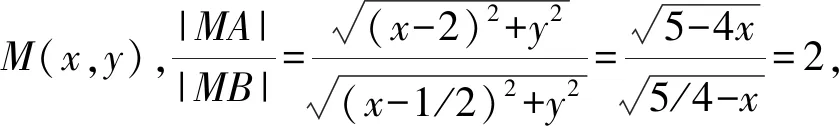
此類題對定點要求比較嚴格,具有一定的局限性,所以一般很少見.

類型3已知一定點A、定比λ和定圓C,求另一定點B.

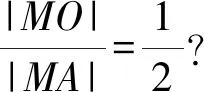
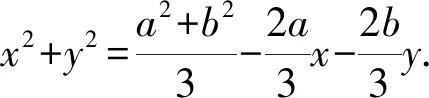
①

又點M在圓(x+1)2+y2=4上,

所以x2+y2=3-2x.

②

對比①②解得a=3,b=0.

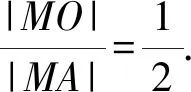
類型4已知一定點A和定圓C,求另一定點B和定比λ.

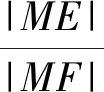
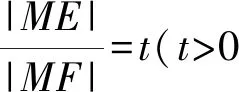
即(x-2)2+y2=t2[(x-m)2+(y-n)2].

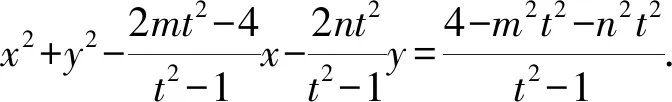
因為M在圓O:x2+y2=1上,

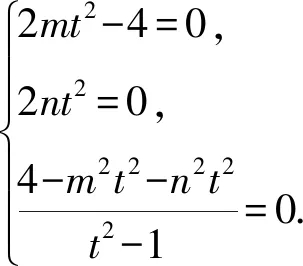
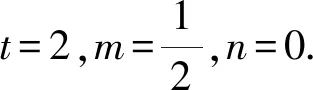
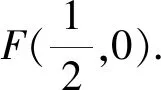
對比兩種解法可以發現,解題時巧妙運用阿氏圓的性質可以大大減少計算量[1].

類型5已知定比λ和定圓C,求定點A和定點B.

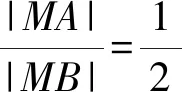
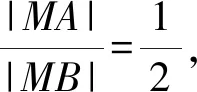
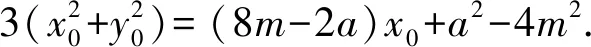
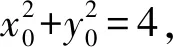
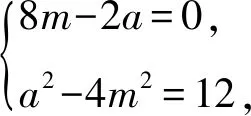
所以兩定點分別為(1,0),(4,0)或(-1,0),(-4,0).

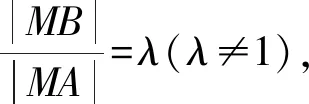
類型6已知定點A和定圓C,求最值或范圍.

阿氏圓常用于解決形如:MA+k·MB(k≠1)類線段的最值問題:其中M是動點,A,B是定點,且動點M在阿氏圓上運動.

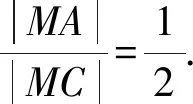
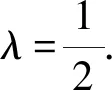
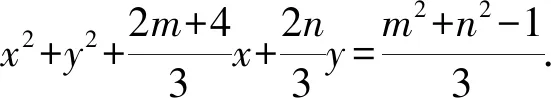
由題意得該圓的方程為x2+y2=1,

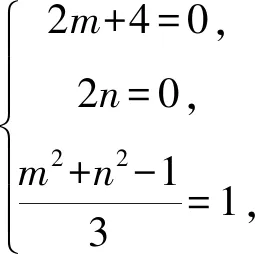
所以點C的坐標為(-2,0).

所以2|MA|+|MB|=|MC|+|MB|.

因此當點M,C,B在同一條直線上時,2|MA|+|MB|=|MC|+|MB|的值最小,且為

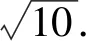
從上面例題中我們可以得到MA+k·MB(k≠1)類問題更加一般性的解題步驟:

運用:動點在圓上運動,兩線段(帶系數)相加求最小值.

形如:MA+k·MB(k≠1)的最小值 (k為系數);

原理:構造共邊共角相似,轉移帶系數的邊,利用兩點間線段最短求最小值.

變式在平面直角坐標系中,已知點A(0, 3), 圓C:(x-a)2+(y-2a+4)2=1.若圓C上存在點M,使|MA|=2|MO|,則實數a的取值范圍是____．

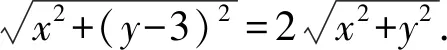
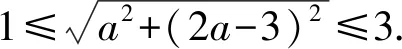
類型7阿氏圓在復數,三角等問題中的應用.

例7設復數z=x+yi(x,y∈R),且|z-1|=2|z+1|,則復數z所對應的點的軌跡形狀是____.

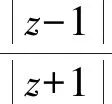
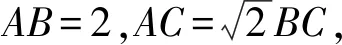
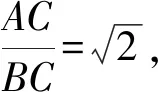
阿氏圓的應用十分廣泛,高中階段充分掌握阿氏圓的概念及其性質是必要的,在實際解題中靈活運用會給我們帶來意想不到的效果.