巧用動(dòng)量定理解決電磁場(chǎng)中粒子復(fù)雜運(yùn)動(dòng)的問題

王漢權(quán)

(江蘇省錫山高級(jí)中學(xué),江蘇 無錫 214174)

在處理電磁場(chǎng)中粒子運(yùn)動(dòng)時(shí),學(xué)生一般都會(huì)采用描繪軌跡、尋求幾何關(guān)系或利用洛倫茲力不做功的特點(diǎn)結(jié)合動(dòng)能定理解題,但有時(shí)會(huì)遇到粒子在若干電場(chǎng)、磁場(chǎng)交替的組合場(chǎng)或疊加場(chǎng)的物理情境,運(yùn)動(dòng)情況非常復(fù)雜,軌跡也很難直觀去描繪,動(dòng)能定理有時(shí)也會(huì)相形見絀.這時(shí)候,如果注意到粒子兩個(gè)方向速度變化引起的洛倫茲力的沖量Ix=∑Bvyq·Δt=∑BqΔy和Iy=∑Bvxq·Δt=∑BqΔx,再結(jié)合粒子運(yùn)動(dòng)過程始末狀態(tài)的動(dòng)量變化,就可以利用動(dòng)量定理輕松突破因軌跡難描繪、過程難分析等解題瓶頸,從空間和時(shí)間兩個(gè)維度上完美解決粒子復(fù)雜運(yùn)動(dòng)的問題.

1 典型案例研究

例1在如圖1所示的xOy空間中有兩段連續(xù)的磁感應(yīng)強(qiáng)度分別為B1和B2的勻強(qiáng)磁場(chǎng)(B1=2B2),磁感應(yīng)強(qiáng)度方向均垂直紙面向里,兩段勻強(qiáng)磁場(chǎng)寬度分別為d1和d2(d1=d2),現(xiàn)有一質(zhì)量為m、帶電為+q的粒子從坐標(biāo)原點(diǎn)O沿x正方向以速度v0射入磁場(chǎng)B1,求粒子離開磁場(chǎng)B2時(shí)速度與水平方向偏角θ2的正弦值.

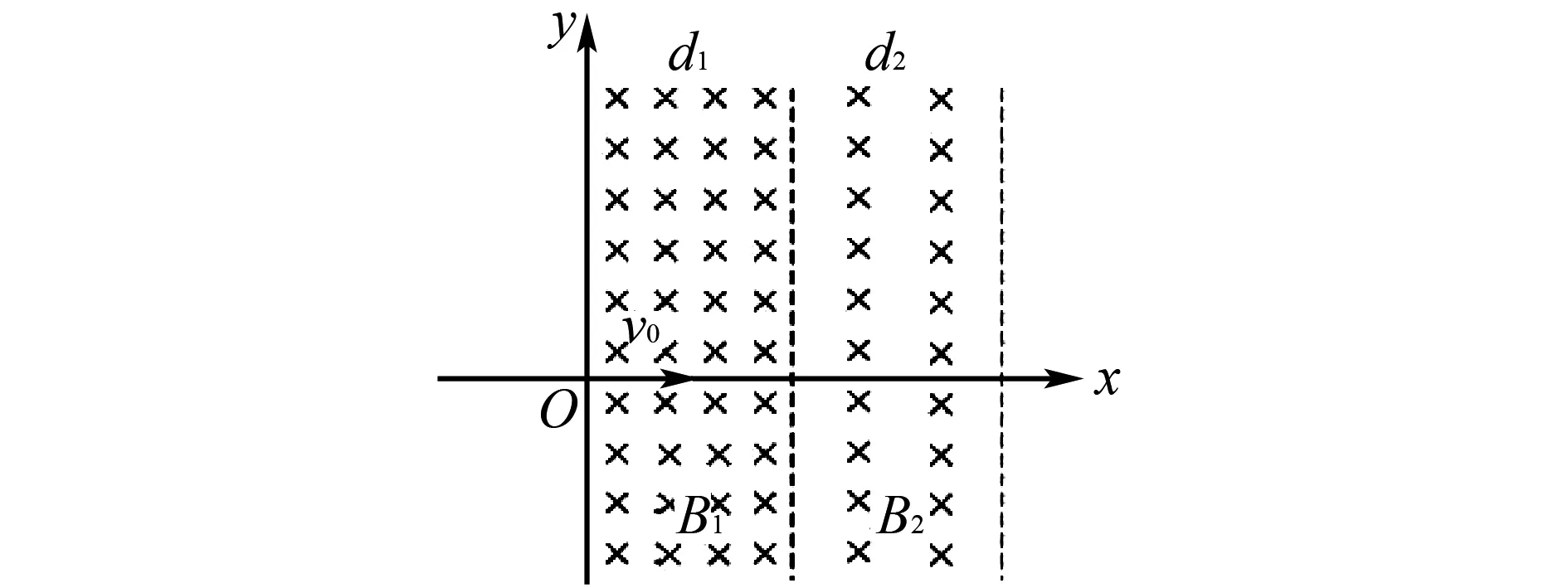
圖1 例1圖

1.1 模型建構(gòu)剖析

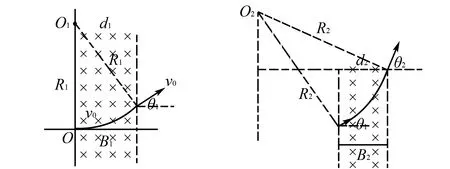
圖2 模型1示意圖 圖3 模型2示意圖

1.2 思路變換求新

解題中采用了較為常規(guī)的畫軌跡找關(guān)系的思路,所以解題著重在尋找前后磁場(chǎng)間的半徑R與偏角θ間的數(shù)學(xué)關(guān)系.如果我們不單注意洛倫茲力提供向心力的動(dòng)力特征和洛倫茲力不做功的能量特征外,再深層次分析洛倫茲力f作用的沖量If,由于粒子速度方向不斷變化,因此粒子所受洛倫茲力f的沖量并不為零!x方向上:洛倫茲力沖量Ifx是由Bvyq引起,即

-∑Bvyq·Δt=m(vx-v0)

①

y方向上:洛倫茲力沖量Ify是由Bvxq引起,即

∑Bvxq·Δt=mvy-0

②

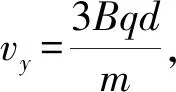
1.3 方法總結(jié)體悟

利用動(dòng)量定理來處理粒子復(fù)雜運(yùn)動(dòng)的問題,可以省去復(fù)雜軌跡不易描繪、幾何關(guān)系不易尋找、運(yùn)動(dòng)過程較難細(xì)致分析的麻煩,巧妙利用某一方向(如x方向)上位移x的累加Bq∑Δx或磁場(chǎng)B、位移x的累加q∑BΔx,與相垂直的方向(y方向)上動(dòng)量變化m(Δvy)間構(gòu)建了相互關(guān)聯(lián),充分表現(xiàn)出動(dòng)量定理在此類問題中的解題優(yōu)勢(shì).

例2(2008高考江蘇卷)在xoy坐標(biāo)系中有一場(chǎng)強(qiáng)為B的水平勻強(qiáng)磁場(chǎng),質(zhì)量m、帶電+q的小球從原點(diǎn)O靜止釋放,小球運(yùn)動(dòng)軌跡曲線如圖4所示．已知此曲線在最低點(diǎn)時(shí)曲率半徑為該點(diǎn)到x軸距離的2倍,重力加速度取g．求:

圖4 例2圖

(1) 問略;

(2)小球在運(yùn)動(dòng)過程中第一次下降的最大距離yM.

解法1(高考卷標(biāo)準(zhǔn)解答):略

解法2(運(yùn)動(dòng)合成分解法):利用Bvxq=mg得到

③

④

解法3(動(dòng)量定理法):粒子運(yùn)動(dòng)到最低點(diǎn)時(shí),重力做功最多,所以速度最大vM且水平向右.之所以水平方向上速度從0變?yōu)関M,其實(shí)是粒子水平方向洛倫茲力fx與時(shí)間t累積的結(jié)果,利用動(dòng)量定理∑Bvyq·Δt=m(vm-0)[2],而∑Bvyq·Δt=Bqym,所以

Bqym=mvm-0

⑤

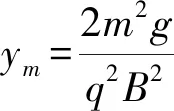
綜合上述的三種不同解法,足可以看出當(dāng)運(yùn)動(dòng)過程比較復(fù)雜時(shí),動(dòng)量定理解題不需要在過程細(xì)節(jié)上花費(fèi)過多精力,但也需要有明確的審題導(dǎo)向:(1)過程多變復(fù)雜、幾何關(guān)系不容易尋找;(2)某一個(gè)方向上出現(xiàn)清晰的速度變化;(3)對(duì)應(yīng)另一個(gè)垂直方向上的位移累積量或磁場(chǎng)B和位移的累積量清晰呈現(xiàn),這時(shí)候 就可以優(yōu)先考慮選擇動(dòng)量定理來處理.此解法方向明確、方便快捷,同時(shí)又能避免題中“已知此曲線在最低點(diǎn)的曲率半徑為該點(diǎn)到x軸距離的2倍”多余條件和“曲率半徑”等多余概念的干擾.

2 規(guī)律遷移運(yùn)用

2.1 粒子在若干連續(xù)電場(chǎng)、磁場(chǎng)組合場(chǎng)中復(fù)雜運(yùn)動(dòng)的處理

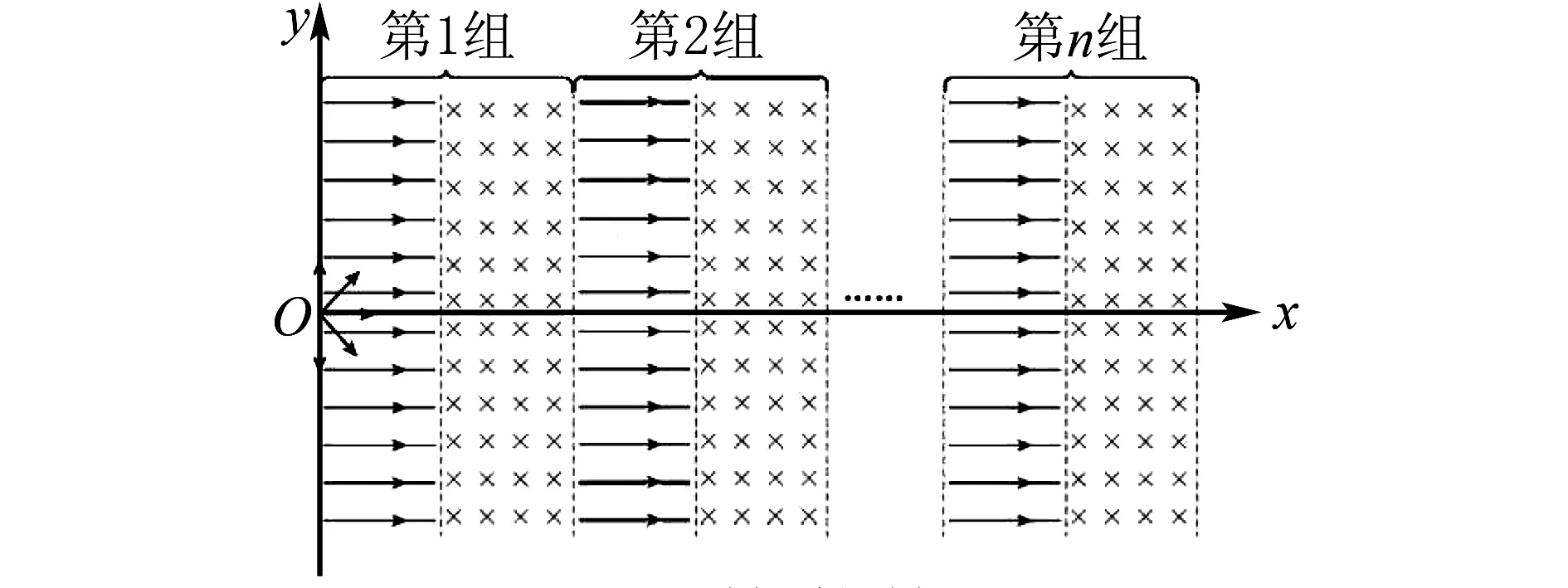
圖5 例3圖

解法1(常規(guī)尋求關(guān)系):略

解法2(動(dòng)量定理法):粒子在第n層磁場(chǎng)恰好不能穿出,此時(shí)速度與邊界相切且方向向上,設(shè)速度為vyn,在第n組磁場(chǎng)中圓周運(yùn)動(dòng)的半徑為rn(下標(biāo)表示粒子所在組數(shù)),根據(jù)動(dòng)能定理得

⑥

再分析x、y兩個(gè)方向的運(yùn)動(dòng),電場(chǎng)方向始終沿水平方向,并不能改變粒子在y方向的速度(動(dòng)量),則從靜止釋放至恰好與第n組磁場(chǎng)邊界相切,在y方向上應(yīng)用動(dòng)量定理得

⑦

圖6

2.2 粒子在電場(chǎng)、磁場(chǎng)等疊加場(chǎng)中復(fù)雜運(yùn)動(dòng)的處理

例4(2013福建高考卷) 如圖7(a)所示,空間存在一范圍足夠大的垂直于xOy平面向外的勻強(qiáng)磁場(chǎng),磁感應(yīng)強(qiáng)度大小為B.讓質(zhì)量為m、電荷量為q(q>0)的帶電粒子從坐標(biāo)原點(diǎn)O沿xOy平面以不同的初速度大小和方向入射到該磁場(chǎng)中．不計(jì)重力和粒子間的影響.(1)(2)問略.(3)如圖7(b)所示,若在此空間再加入沿y軸正向、大小為E的勻強(qiáng)電場(chǎng),一粒子從O點(diǎn)以初速度v0沿y軸正方向發(fā)射．研究表明:粒子在xOy平面內(nèi)做周期性運(yùn)動(dòng),且在任一時(shí)刻粒子速度的x分量vx與其所在位置的y坐標(biāo)成正比,比例系數(shù)與場(chǎng)強(qiáng)大小E無關(guān)．求該粒子運(yùn)動(dòng)過程中的最大速度值vM[3].

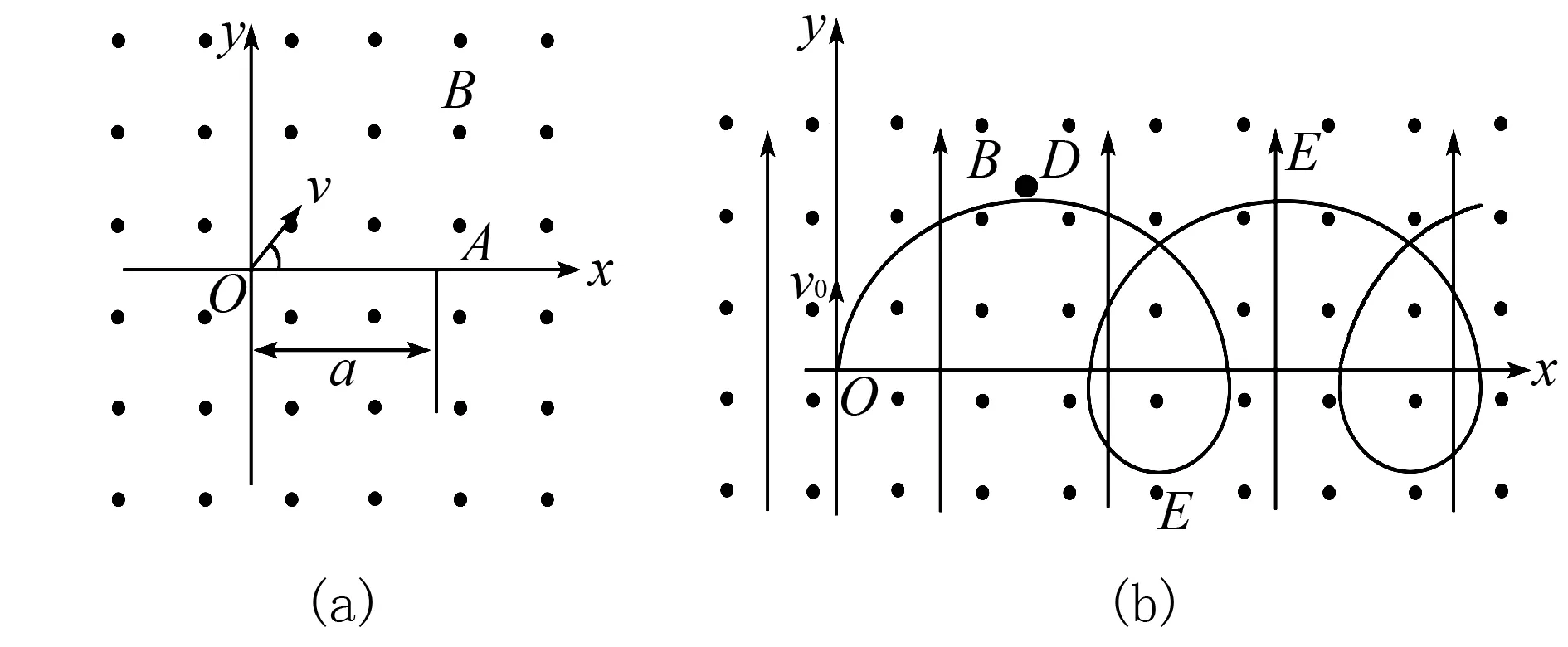
圖7 例4圖

解法1(高考卷標(biāo)準(zhǔn)解答):結(jié)合軌跡可知,粒子運(yùn)動(dòng)到D點(diǎn)時(shí)沿電場(chǎng)方向位移yM最大,速度最大且沿水平方向,有

⑧

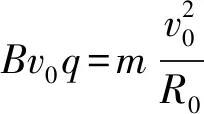
⑨

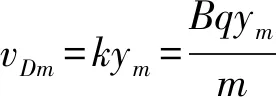
代入⑧式解出得

⑩

該解法比較常規(guī),但尋求關(guān)系不容易,運(yùn)算也較煩瑣.

解法2(動(dòng)量定理解題): 粒子從O點(diǎn)運(yùn)動(dòng)到D點(diǎn),水平方向速度從0變?yōu)関Dm,此速度變化是由粒子洛倫茲力Bvyq與時(shí)間t累積引起,由動(dòng)量定理得

∑Bvyq·Δt=Bqym=m(vDm-0)

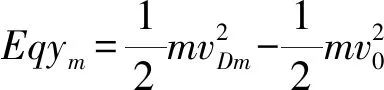
從案例剖析到解法變換,可以看到處理粒子復(fù)雜運(yùn)動(dòng)的問題有多種解題方法,但不管選用哪種解法,也不管試題設(shè)置情境或所給條件發(fā)生什么樣的新穎變化,解題中一定要養(yǎng)成認(rèn)真分析粒子受力和過程變化的良好習(xí)慣,還要重視一些關(guān)鍵信息的審題(如水平速度、最大速度、曲率半徑、恰好離開磁場(chǎng)等),然后就可以嘗試采用動(dòng)力學(xué)或能量的觀點(diǎn)進(jìn)行解題.當(dāng)然如果發(fā)現(xiàn)仍然無法求解或解題過于復(fù)雜、繁瑣等情況時(shí),就應(yīng)當(dāng)快速定位選用動(dòng)量的觀點(diǎn)來解題.最后要說明一點(diǎn)是動(dòng)量定理是反映合外力沖量與物體動(dòng)量變化的規(guī)律, 因此使用動(dòng)量定理時(shí)一定要構(gòu)建物體所受的合力沖量和對(duì)應(yīng)過程的動(dòng)量變化的關(guān)聯(lián),如在例3中,之所以輕松地用∑Bvxq·Δt=mΔvy求解y方向上速度變化,是因?yàn)榱Ｗ釉趛方向上僅存在由vx引起的洛倫茲力fy,但如果確實(shí)需要研究x方向上的運(yùn)動(dòng)情況,則需要加上電場(chǎng)力的沖量,建立∑(Eq-Bvyq)·Δt=mΔvx的方程,化簡(jiǎn)得到Eq·t-Bq(y1+y2+…)=m(0-v0),倒是可以求解出粒子在電場(chǎng)中總時(shí)間t或粒子在所有磁場(chǎng)中運(yùn)動(dòng)y的累加量.