三角恒等變換視角下構建圓錐曲線參數方程

金 毅

(呼和浩特市第二中學,內蒙古 呼和浩特 010000)

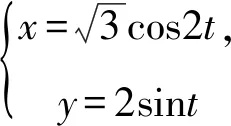
解決這三個問題的主要思路是消參,通過配湊和換元消去參數t,進一步得到對應的方程.

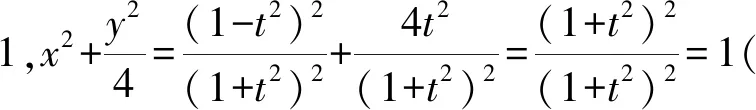
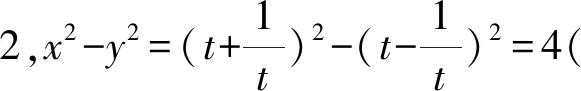
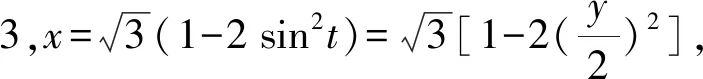
以上三個問題屬于求解軌跡方程的問題,且均為參數方程的形式,解決問題的過程并不復雜.從求解的結果來看,三道題目分別對應橢圓、雙曲線和拋物線.從表象來看,似乎這些參數方程并未在我們學習的課本當中正式呈現,但在題目中卻頻繁考查,難道是高考的方向與教材脫鉤?事實上,經過我們的分析,結論卻恰恰相反,這幾道題目正是來源于教材中的圓錐曲線參數方程.我們將從三角函數恒等變換的視角對以上問題的背景進行探討.

1 三角恒等變換視角下的圓錐曲線參數方程

1.1 對橢圓參數方程的探討

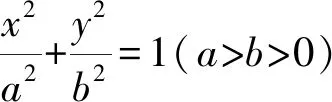
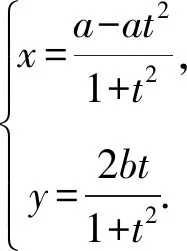
因t=tan(θ/2),且0≤θ≤2π,可知θ≠π.這樣我們得到的參數方程無法表示橢圓上的所有點.

綜上,橢圓的一個參數方程為

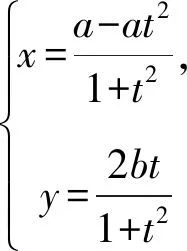
①

點評結合以上討論,可知①式是問題1的背景知識,問題1對應①式中令a=1,b=2時的情形.①式得到的過程主要依托于三角恒等變換中的萬能公式,在恒等變換公式的加持下,得到了分式結構特征的橢圓參數方程.從這個角度來說,問題1的背景知識源于課本,但是經過了恒等變換公式的“精加工”,使得題目的呈現高于課本.同時,因橢圓是中心對稱圖形,則橢圓的另一個參數方程為

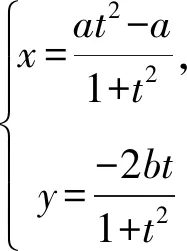
②

1.2 對雙曲線參數方程的探討

令t=tan(θ/2),可得雙曲線的一個參數方程為

③

我們基于恒等變換,得到了雙曲線的一個參數方程.我們看到,②式與問題2的匹配程度存在差異,似乎是一次不成功的代數變形.但是,②式的推導思路為我們推導另一個雙曲線的參數方程提供了思路,為我們打開了另一扇大門.

令t=tan(θ/2),得雙曲線的另一個參數方程為

④

點評③④式本質上是對三角恒等變換平方關系進行換元,并做進一步運算,結合萬能公式得到最后結果.事實上,對于④,因雙曲線是關于x軸對稱的圖形,故我們得到以下公式

⑤

可知,⑤式也是雙曲線的一個參數方程.因此⑤式為問題2的背景知識,只需令a=2,b=2即可得到問題2.

從以上討論可看出,對于橢圓、雙曲線標準方程下的某個參數方程,我們可以根據曲線的對稱性,靈活調配正負系數,得到新的參數方程.

1.3 對拋物線參數方程的探討

事實上,對拋物線(y-y0)2=-2p(x-x0),可得其參數方程為

⑥

以上參數方程,表示開口向左,且頂點在(x0,y0)處的拋物線.

點評問題3的命制本質就是在⑥式的基礎上進行了簡單的三角恒等變換得到新的題干.

2 反思與學習建議

從以上討論過程發現,在高考的命題中,有相當一部分題目的背景源于教材.可以說,教材作為高考命題的“題源”,有非常大的學習和思考的價值[1].以下給出幾點建議,以幫助大家做好對教材的學習和挖掘.

2.1 重視數學教材中對知識的研究視角

教材對橢圓參數方程、雙曲線參數方程研究的出發點是三角恒等式的“平方關系”,這說明教材非常重視通過恒等變換的研究視角得到參數方程.所以,在后續的學習中,不僅要重視教材的基本知識內容,更要在研究方法上增強其“延續性”,也就是沿著教材給出的研究視角進一步探索新的知識.

2.2 重視數學教材中的例題

數學教材中例題及其解答過程的呈現,向我們展示了數學問題從提出到解決的完整過程.首先要重視問題提出的形式,弄清在不同的視角下呈現的形式是什么.如橢圓的參數方程在三角恒等變換下會有不同的呈現形式.其次是例題的解法.教材中例題的解法會向我們呈現解決問題的一般方法,也就是通法,要加以積累和思考.

2.3 重視數學教材中的章節起始課

文獻[1]中指出,教材中章、節的引言和小結往往都給出了研究一個數學對象的基本套路.其基本要點為:背景——概念——性質——結構——應用.其中,背景指現實世界中的一類現象;概念明確了研究對象;性質是在概念基礎上,明確概念的要素與相關要素之間的關系、變化規律等;結構是相關知識的聯系;最后再進行綜合應用.所以,章節起始課的重要性不言而喻.

本文將高考試題與教材知識結合,闡釋其來龍去脈,強調教材知識與研究視角的重要性,給出學習建議,希望能開拓大家學習數學的思路,提升解決相關問題的能力.