用活“主元” 所向披靡

魯和平

(浙江省嘉善第二高級中學,浙江 嘉善 314100)

一道數學題中,一般含有很多個變量、參數、常數.如果能根據題目要求,打破常規,不拘一格,確定一個處于突出主導地位的元素為“主元”,則解題思路豁然開朗.如何靈活機智地確定“主元”,巧妙地運用“主元法”解題,則要因題制宜,審時度勢.

1 反客為主,出奇制勝

在方程或函數里,自變量與參數的地位不是一成不變的,看問題的視角不同,就會發生戲劇性的變化.

例1設方程x2+ax+b-2=0(a,b∈R) 在(-∞,-2]∪[2,+∞) 上有實數根,求a2+b2的取值范圍.

解析本題若直接由條件出發,利用實根分布條件求出a,b滿足的條件,亦可獲解,但過程繁瑣.在此,我們反客為主,視方程x2+ax+b-2=0(a,b∈R)為aOb坐標平面上的一條直線:l:xa+b+x2-2=0,且P(a,b)為直線上的點,則a2+b2=|PO|2, 設d為點O到直線l的距離,由幾何條件知:

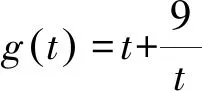
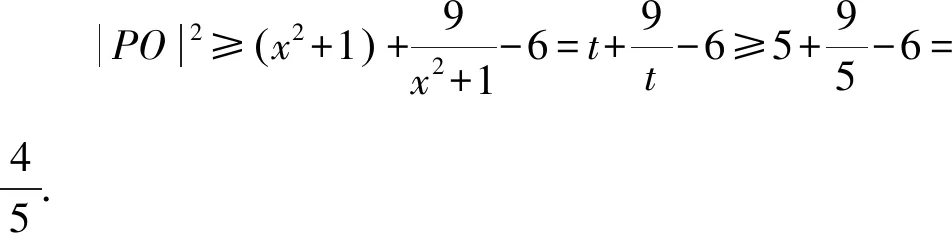
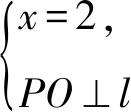
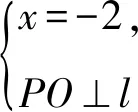
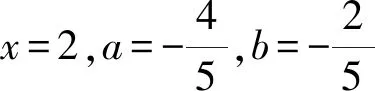
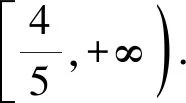
例2 設f(x)=(1+a)x4+x3-(3a+2)x2-4a,對任意實數a,試證明:

(1)方程f(x)總有一個相同的實數根;

(2)存在x0∈R,恒有f(x0)≠0.

解析將f(x)以a為主元整理,得

f(x)=(x4-3x2-4)a+(x4+x3-2x2).

即f(x)=(x-2)(x+2)(x2+1)a+x2(x-1)(x+2).

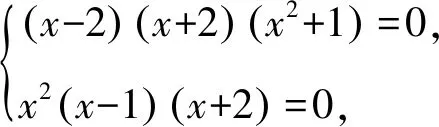
因為對任意實數a,總有f(-2)=0,故對任意實數a,方程f(x)=0總有實數根x=-2.

因為對任意實數a,有f(2)=16≠0,

故對任意實數a,存在x0=2,恒有f(x0)=16≠0.

2 巧設主元,迅速降冪

對于高次方程(或函數),可以通過整體換元的方式,達到降冪的效果.

例3設a,b∈R, 滿足2a+b+2≤0.證明:方程x4+ax3+bx2+ax+1=0 至少存在一個正實數解.

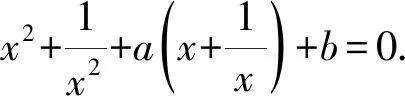
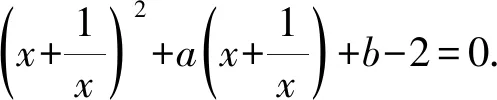
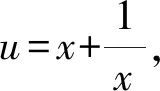
3 咬定主元,巧設函數

對于多變量的不等式問題,可以咬定其中一個作為主元,再運用函數的方法加以解決.

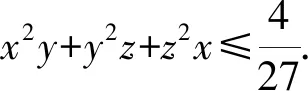
由x+y+z=1,得z=1-x-y.

則x2y+y2z+z2x=x2y+y2(1-x-y)+(1-x-y)2x.

視x為主元,

設f(x)=x2y+y2(1-x-y)+(1-x-y)2x

=x3+(3y-2)x2+(1-2y)x+y2-y3,

=(3x-1)[x-(1-2y)].

因為x-(1-2y)=x+2y-1=(1-y-z)+2y-1=y-z≤0,

所以f′(x)≥0,

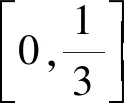
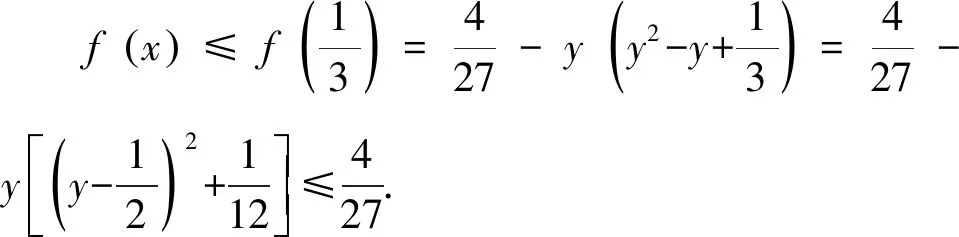
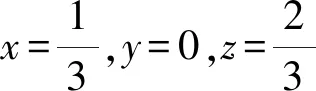
4 變中求定,固定主元

在多變量題目中,如果每個變量地位相同,可選擇其中一個為主元,并將其固定,減少變量個數,化陌生為熟悉.

多關注自己的晚年生活。老人將兒女養育成人很不容易，承受了太多艱辛。兒女長大成人，有了自己的事業和生活，正是父母徹底放手的最佳時機。放下“一輩子為兒女活”的思想，打開“為自己而活”的晚年生活模式，養花種草、背包遠游、上老年大學、跳廣場舞，快樂地享受晚年生活。

例5在△ABC中,求y=sinAsinBsinC的最大值.

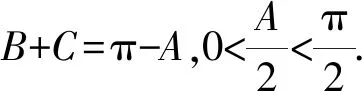
所以y=sinAsinBsinC

固定A, 由于sinA>0,

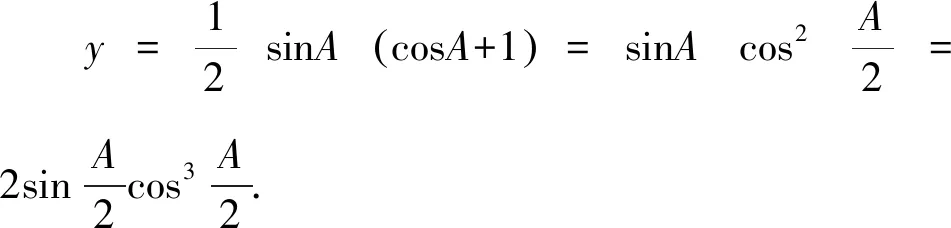
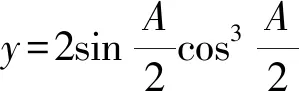
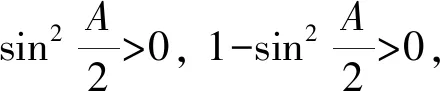
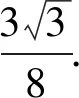
5 多管齊下,水到渠成

“主元法”大多是處理“代數問題”,但“代數問題”的求解往往是多姿多彩的.因此,解題時,除了確定“主元”外,還要善于靈活運用多種“代數問題”的解題技巧與手段.

例6已知a,b,c∈R, 且a+b+c=12,ab+bc+ca=45, 試求abc的最大值.

解析由a+b+c=12 ,得a+c=12-b.

代入ab+bc+ca=45 的變形式b(a+c)+ca=45,得b(12-b)+ca=45.

即ca=b2-12b+45.

即b2-8b+12≤0.

所以2≤b≤6.

于是abc=(b2-12b+45)b=(b-3)2(b-6)+54≤54.

不難得到,當a=3,b=6,c=3 或a=6,b=3,c=3 或a=3,b=3,c=6 時,abc取得最大值54.

6 韋達定理,減元神速

韋達定理是涉及兩個變量的兩個等式,有的還與參數建立聯系.這就為我們減元提供了思路,隨著元的個數減少,主元隨即凸顯出來.

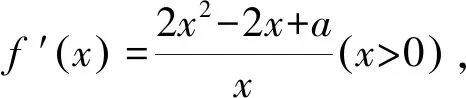
由x1+x2=1,得x1=1-x2,x2-1=-x1,

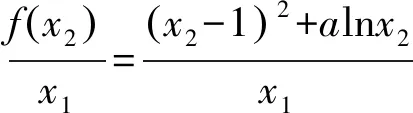
=x1+2x2lnx2

=1-x2+2x2lnx2.

g′(x)=2lnx+1.

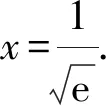
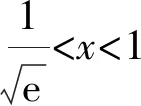
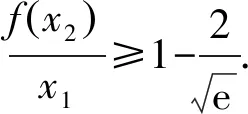
7 巧換主元,妙手回春

有些問題的主元只有一個,并且非常顯露,但要求解,則無從下手.這時要善于研究式子的結構特征,迅速聯想,巧妙換元,將情景化為我們非常熟悉的問題.

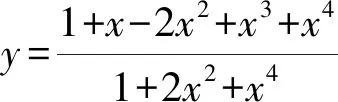
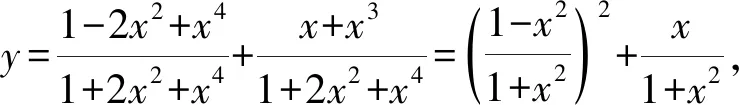
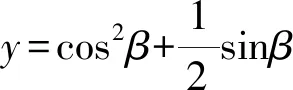
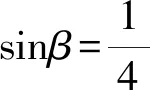
8 輪流做主,同心協力

有些多變量最值問題,可以劃分為幾個階段解決.即在不同的階段選擇不同的主元解決階段性的問題,各個變量輪流做主,完成各自在不同階段的任務.選擇主元意味著消元,直到所有變量消失,則問題解決[1].

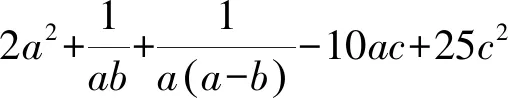
解析先以c為主元并消去c,配方得

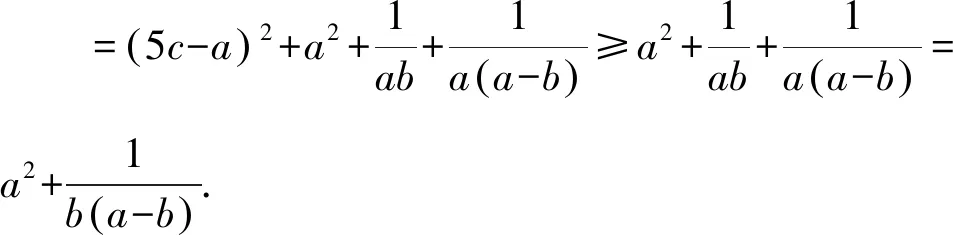
再以b為主元并消去b,由均值不等式,得

最后以a為主元,由均值不等式,得

故所求最小值為4.