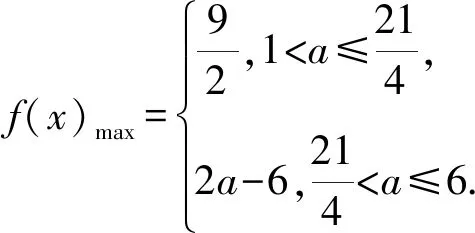基于核心素養下的高一數學復習課
——由一道習題引起的“分段函數”問題淺探

王曉丹

(江蘇省梁豐高級中學,江蘇 蘇州 215600)

剛從初中升上高中的學生普遍不能立刻適應,都覺得高一數學難學,數學成績出現嚴重滑坡,漸漸地他們認為數學神秘莫測,從而產生畏懼心理,動搖了學好數學的信心,甚至失去了學習數學的興趣.如何根據學生現有的認知水平,幫助學生盡快適應高中數學教學特點和學習特點,跨過“高臺階”,成為了高一數學教師的首要任務[1].本文以“分段函數”為例,對高一數學復習課教學進行分析,以發展學生的數學核心素養.

1 分段函數的定義

(1)分段函數是一個函數,而不能誤認為它是幾個函數;

(2)分段函數的定義域是各段函數自變量范圍的并集,值域也是各段函數中y取值范圍的并集.

2 解決分段函數的兩種思想

2.1 分類討論,面面俱到

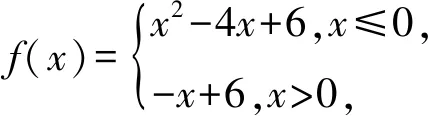
解析因為f(-1)=11,

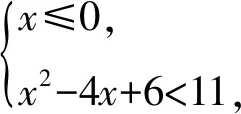
綜上,x的取值范圍是(-1,+∞).

點評解方程、不等式或求取值范圍時,應該根據自變量的分段范圍把分段函數問題轉化為不同區間上的方程、不等式(組)求解,然后再取這些方程、不等式(組)解集的并集.

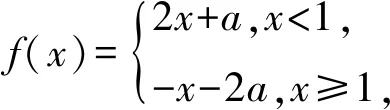
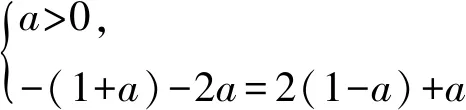
2.2 數形結合,化繁為簡

分段函數雖然分段,但是當遇到常規思路進行處理難以奏效或計算冗繁的時候,通過分析分段函數的數量及圖形特征,可以嘗試從整體著眼,跳過常規解題步驟,尋求解決問題的方法,這是分段函數考查的一個重要方面[2].

3 分段函數的幾類問題

3.1 分段函數奇偶性相關問題

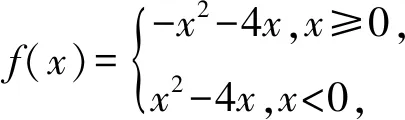
在思考本題時,學生很容易作出函數的圖象,但對于f(a-2)+f(a)>0的處理會出現困難,嘗試得到f(a-2)>-f(a),觀察所作圖象及奇函數定義可以判斷出函數f(x)為奇函數,那么式子可以變形得到f(a-2)>f(-a),結合圖象得到f(x)在R上單調遞減,所以a-2<-a,解得a<1.

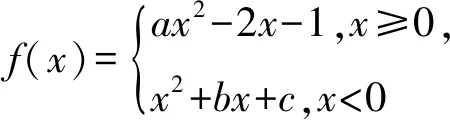
分析本題有兩個難點需要突破,首先要求解出a,b,c的值,可以利用分段函數的奇偶性:

當x>0時,f(x)=ax2-2x-1,則-x<0,f(-x)=(-x)2+b(-x)+c=x2-bx+c=ax2-2x-1.

利用待定系數法,我們很快能得到a=1,b=2,c=-1.

第二個難點是學生對于解的個數的理解,方程的解可以轉換為兩個函數圖象y=f(x)和y=t的交點問題,結合偶函數圖象,得到實數t的取值范圍是(-2,-1).

3.2 分段函數單調性問題

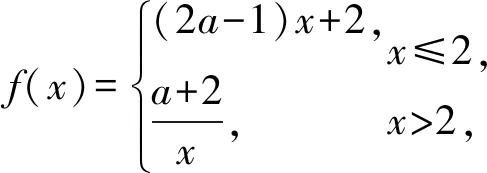
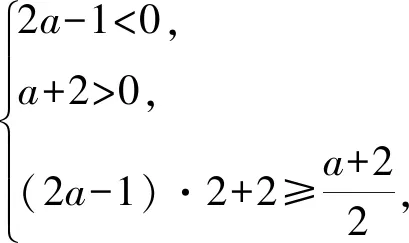
3.3 絕對值函數的單調性問題

對于函數解析式中帶有絕對值的問題,我們該怎樣來求它的單調區間和最值呢?

絕對值函數問題初看上去不是一個分段函數,但根據絕對值意義分類討論后,去掉絕對值,其本質仍然是分段函數問題.

變式7 已知函數f(x)=|x|(x-a)(a<0),求f(x)的單調區間.

變式8 設函數f(x)=-x2+a|x-1|,若f(x)在(0,+∞)上單調遞減,求實數a的取值范圍.

4 絕對值函數的最值問題

分析因為1

羅增儒教授曾把解題總結為“條件預示可知并啟發解題手段,結論預告須知并誘導解題方向”.我們一線教師的根本任務就是幫助學生把一個個具體知識理解到位,并能用于解決實際問題.這要求我們在日常教學中,要思考和貫徹新理念方法,從不同層面幫助學生進一步加深對分段函數的理解并靈活應用,從而在數學知識的教學中尋找發展學生數學核心素養的途徑.