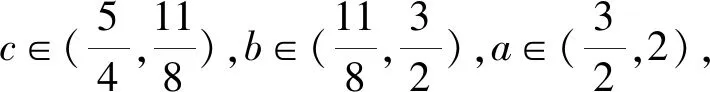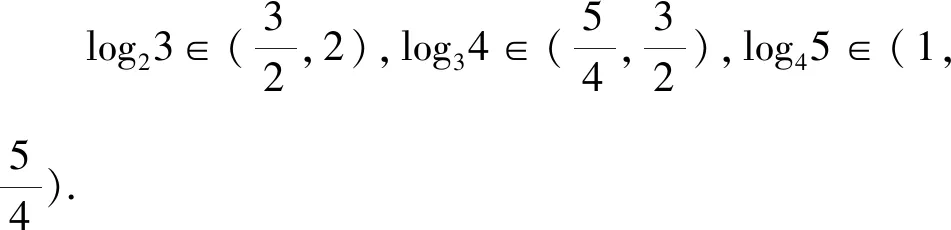2020年全國Ⅲ卷理科第12題新解及命題思路探究
代紅軍 何 波
(1.云南師范大學(xué)數(shù)學(xué)學(xué)院,云南 昆明 650500;2.昆明市官渡區(qū)第六中學(xué),云南 昆明 650500)
對數(shù)比較大小是高考的熱點和難點題型,主要以填空題、選擇題的形式出現(xiàn),試題難度大.近幾年試題展現(xiàn)出一定的創(chuàng)新性,考查學(xué)生的數(shù)學(xué)運算、數(shù)據(jù)處理、數(shù)學(xué)抽象等核心素養(yǎng),要求學(xué)生掌握必備的知識和解決此類問題的關(guān)鍵能力.筆者對《數(shù)理化解題研究》2022年第34期文章《對數(shù)比較大小試題的解法探究兩例》中變式應(yīng)用環(huán)節(jié)的變式1解法提出疑問,指出錯誤原因并給出新解.
1 問題提出
《數(shù)理化解題研究》2022年第34期《對數(shù)比較大小試題的解法探究兩例》變式應(yīng)用環(huán)節(jié)的變式1.
變式1設(shè)a=log23,b=log35,c=log58,則( ).
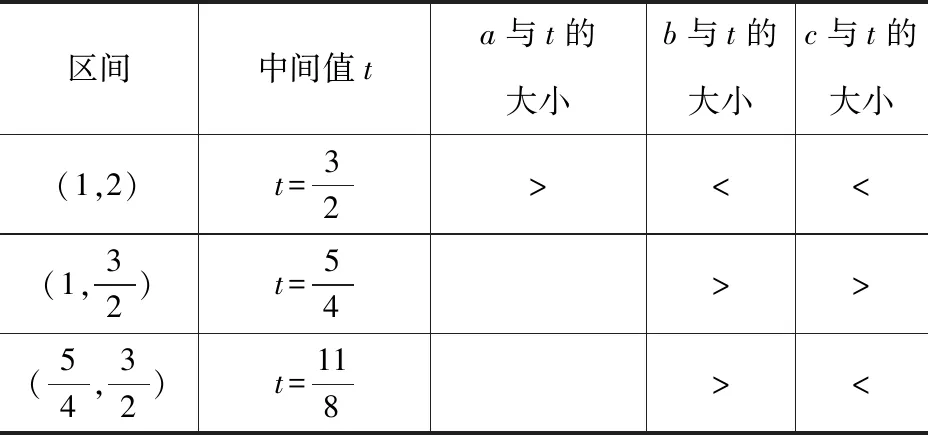
A.a C.a 同理可得log35 題目(2020年全國Ⅲ卷理科第12題)已知55<84,134<85.設(shè)a=log53,b=log85,c=log138,則( ). A.a C.b 分析試題命制的創(chuàng)新之處是給出了一組參考數(shù)據(jù),如何運用參考數(shù)據(jù)是破解此題的關(guān)鍵,不同的運用方式能帶來不同的解法,我們從三個角度運用參考數(shù)據(jù),提煉出新的解法. 因為b=log85,得8b=5.所以85b=55<84. 針對上面兩個問題,筆者提出對數(shù)比較大小的另一種方法,叫二分法尋找中間量.方法介紹及操作流程,筆者通過具體例題呈現(xiàn).2020年全國Ⅲ卷理科第12題如不用參考數(shù)據(jù),得到如下變式[1]. 變式設(shè)a=log53,b=log85,c=log138,則( ). A.a 應(yīng)用1《數(shù)理化解題研究》2022年第34期文章《對數(shù)比較大小試題的解法探究兩例》變式應(yīng)用環(huán)節(jié)的變式1. 正解顯然a,b,c∈(1,2). 表1 應(yīng)用1的解析過程 應(yīng)用2(必修第一冊第141頁第13題(2))比較log23,log34,log45的大小. 解析顯然log23∈(1,2),log34∈(1,2),log45∈(1,2). 表2 應(yīng)用2的解析過程 用二分法尋找對數(shù)比較大小的中間量的方法,能明確命題人命制試題的思路和意圖,在教學(xué)和考試中可以對試題進(jìn)行改編,發(fā)揮試題的變式教學(xué)功能,實現(xiàn)一題一課、一法多用的教學(xué)作用.教學(xué)過程要體現(xiàn)“學(xué)生主體、教師主導(dǎo)、問題主線、思維主攻”的思想[2],對數(shù)比較大小方法多樣,教師從不同視角提出問題,引導(dǎo)學(xué)生主動探究不同的解法,發(fā)現(xiàn)不同解法之間的關(guān)聯(lián),有助于發(fā)展學(xué)生思維.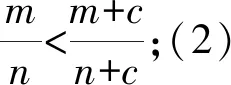
2 新解探究
2.1 高考試題再現(xiàn)
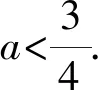
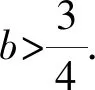
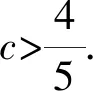
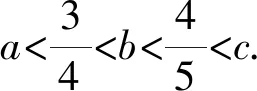
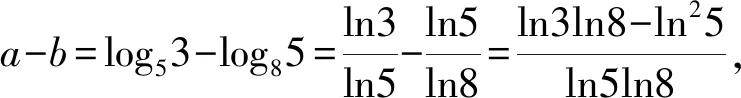

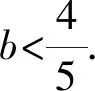
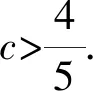
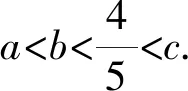
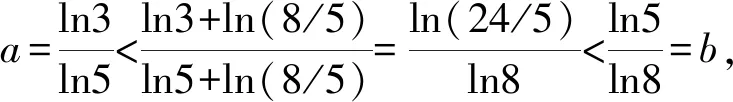
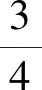
2.2 新解呈現(xiàn)
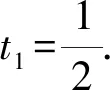
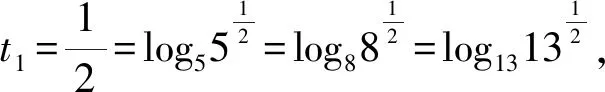
3 新解應(yīng)用