基于追日測控系統中跟蹤裝置定零算法的研究

溫歡，楊治山，楊沂霖

（1.天水電氣傳動研究所集團有限公司，甘肅 天水 741020；2.大型電氣傳動系統與裝備技術國家重點實驗室，甘肅 天水 741020；3.甘肅省民族法制文化研究所，甘肅 蘭州 730030）

在太陽能發電領域，光熱跟蹤發電已成為研究的重要課題，光熱發電跟蹤裝置由于自身機械問題和太陽光線入射等因素的影響，導致跟蹤精度和準確度大大降低，該算法的研究對象是太陽能集熱發電裝置的追日測控系統，特別是涉及一種跟蹤裝置零點確認的算法。

1 系統簡介

1.1 硬件配置

追日測控系統以自動跟蹤集熱發電系統為主體，跟蹤裝置監控、電磁閥自動調度和視頻監控為輔助，將斯特林發動機的運行狀態、監測參數、腔體密閉性、動態視頻、信號燈狀態、氣路狀態和調度信息直觀地在計算機上集中監視。跟蹤裝置與控制室之間實現局域網絡無線覆蓋，實現跟蹤裝置和斯特林發動機的數據交互，即跟蹤系統遠程遙控、伺服電機遠程控制和電磁閥控制，保障發電的安全高效，實現追日測控系統的整體監測［3］。如圖1所示為跟蹤裝置原理圖。

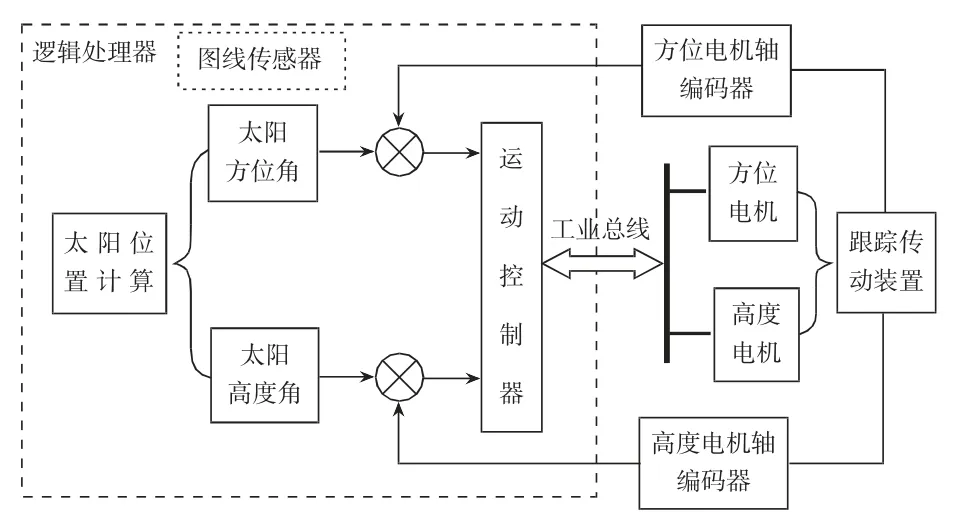
圖1 跟蹤裝置原理圖

1.2 跟蹤的基本依據

跟蹤太陽位置最為常用的是地平坐標系和極軸坐標系。一般工程中采用地平坐標系統，因為在天球上的所有圓圈中，地平是在自然界中唯一能看到的圓。同時由于鉛垂線所具體代表的垂線，以及由水準儀所定出的水平線是在幾何坐標系中能直接觀測的參考方向，所以地平參考系應用廣泛。在實際觀測中，幾何坐標系是以地方天文地平作為基本參考圈的地平坐標系［2］。因此，此系統采用地平坐標系。如圖2所示為坐標系的建立轉換示意圖。

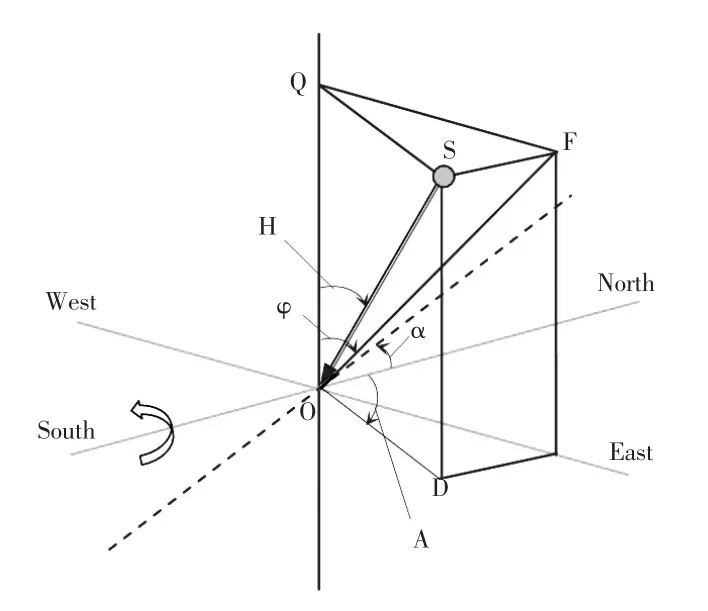
圖2 坐標系的建立轉換示意圖

如圖2所示，在地平坐標系中用太陽高度角H和方位角A表示太陽在天球中的位置。高度角H是指太陽入射光與地平圈之間的夾角；太陽升起地平線與天頂的夾角為90度，正午0度；方位角A是指太陽入射光線在地平面上的投影與地平圈正北的夾角，范圍是0～360°。

當時0°＜A＜90°，φ＝90°；

當時90°＜A＜360°，φ＝Arctan（sinA×tanH）；

太陽跟蹤裝置采用地平坐標系較為直觀方便、操作性強，但也存在軌跡坐標計算沒有具體公式可依賴的問題。而在赤道坐標系中赤緯角和時角在日地相對運動中任何時刻的具體值卻嚴格已知，同時赤道坐標系和地平坐標系都與地球運動密切相關。

在設定跟蹤地點和基準零點后，控制系統會按照太陽的地平坐標公式自動運算太陽的高度角和方位角。那么碟架的零點校準也顯得非常重要，碟架在水平方向和高度方向上采用17位高分辨的編碼器，來反饋碟架的實時位置，對于碟架零位的定義就與太陽方位相一致的思路來校準。任何一地太陽高度最大時，除直射點所在地，太陽總在正南或正北。

正午立于太陽下，或在太陽下豎一竹竿，影子與太陽方位相反，指向正南或正北。如果還不能確定南北，可參考以下情況：如果觀測者在北回歸線以北，一年四季正午太陽直射點都在正南方，影子朝向正北；如果觀測者在北回歸線以南，一年四季正午太陽直射點都在正北方，影子朝向正南；此時如果將碟架發動機伸出支架的影子與竹竿的影子在物理上重合時，確定碟架位置，要比之前更加準確。正北方向和水平確定以后，就可以得知碟架的理論位置，程序里在此理論位置上加入機械校準的差值，不同的碟架對應不同的機械偏差，軟件自適應的靈活性大大提高［2］。

綜上所述，在碟架的零位校準過程中發現，該方法在碟架機械位置如何變化時，都將有機械偏差程序去修訂，零位校準相當靈活，可達到滿意的運行效果。

2 研究過程和方法

2.1 太陽位置的計算

太陽能跟蹤控制系統提供的基于專用控制器的64位天文算法函數庫，它能根據跟蹤器所在地的經度、緯度、大氣壓、溫度、海拔高度、時間差值、大氣折射率，計算出太陽相對于本地的水平角和高度角，計算精度高達±0.0003°；為更好地確定本地的經度、緯度、海拔高度和實現系統的UTC時間同步，控制系統采用GPS接收器接收信號來接收跟蹤裝置所在位置的GPS信息［2］。

本文研究的時間同步采用計算機與控制程序循環中斷的方式，因為控制器時鐘不能時時寫入，這樣會導致控制器內存的浪費和運行速度減慢，所以采用一天校準一次或在規定時間內校準的方式，保證控制器時鐘在允許誤差內，下圖3所示是某地日歷算法程序示意圖，是此地程序運行某日晚八點的記錄截圖。

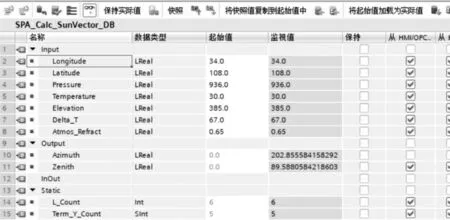
圖3 某地日歷算法程序示意圖

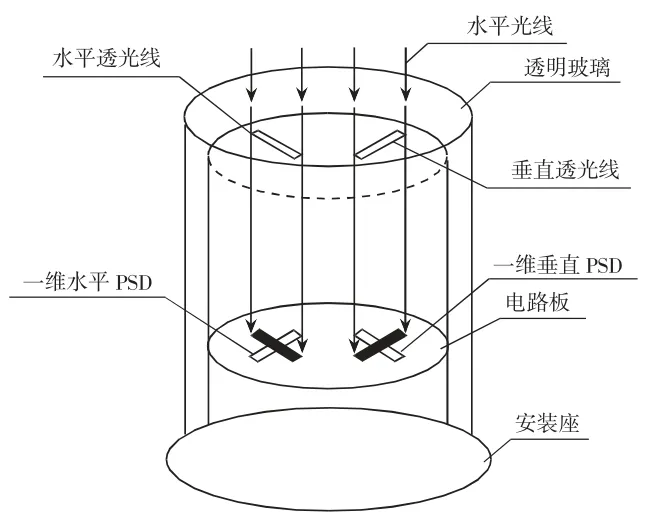
圖4 光線傳感器示意圖

此時太陽的方位角是202.85°，高度角是89.58°，表明此刻已經是晚上。

在實際操作當中，還需要考慮到跟蹤裝置的步進電機、減速機，機械間隙，傳感器等器件，在程序設計中加入校正系數，使得控制精度保持在合理范圍內。

2.2 追蹤裝置定零算法的實現

通過跟蹤裝置俯仰方向上安裝的絕對式光電編碼器,其測量范圍是0-90°,分辨率為16位。

設編碼器在旋轉時輸出的負載位移為εp,其取值范圍是：-32767≤εp≤32767。當跟蹤裝置處于-32767≤εp≤0∪16384＜εp＜32767時，此時設置，λ1＝1，λ2＝0 （λ1、λ2分別是程序執行時的兩個標志位）。而當跟蹤裝置處于0＜εp＜16384區間時，此時設置λ1＝0，λ2＝1。

算法的實現：

如果λ1＝1∩0＜εp成立，且16384＜εp則ζp＝εp，ξLo=ζp-16384，ξHi=εp（ζp實際參（與計算的測量值，ξLo為測量值的下限，ξHi為測量值的上限）；

如果λ2＝1∩εp≤0 成立，且εp≤16384，則ζp＝εp＋65535，ξLo=ζp-16384，ξHi=εp。

由上可得跟蹤裝置俯仰方向上的位置θCadrage＝為工程量上限，為工程量下限。

由跟蹤裝置水平方向上安裝的絕對式光電編碼器,其測量范圍是0-360°，分辨率為16位。設編碼器在旋轉時輸出的負載位移為δp，程序執行過程中，當檢測有外部確認信號后，設置δoffset＝δp，且（δoffset、δp為跟蹤裝置水平方向上的測量值，δManager實際參與運算的數值，為機械偏差）。

當δManager＞0時，ζp1=δManager；當δManager≤0時，ζp1=δManager＋65535；

3 驗證環節

驗證光斑與集熱腔是否重合,需采用一個光線傳感器,這是一種高精度角位移變送器，其夾角以帶符號的十進制的形式輸出，廣泛用于自動化測量與控制系統中，例如：高精度太陽跟蹤、動態瞄準、機構跟蹤等場合。

平行光照射到變送器的透明玻璃窗上,透過玻璃窗下面的兩個互相垂直的平行光照射到變送器的透明玻璃窗上，透過玻璃窗下面的兩條細縫照到PSD上，經過電路處理產生電信號，這個電信號的大小和光線與機箱軸線的夾角成比例，信號的符號與夾角的方向相對應，且成90°夾角，證明跟蹤裝置的焦點、太陽和地心在一條直線上，說明光斑與跟蹤裝置的集熱腔中心是完全重合的。再經過數字化處理變成數字信號通過CAN總線或RS-422/RS-485輸出，同時輸出光強信號。

跟蹤裝置在跟隨太陽運動時，跟蹤裝置的二維坐標（Vertical_Act_Position，Level_Act_Position）和太陽系坐標（Azimuth，Zenith）如下圖5所示，在跟蹤裝置的二維坐標中監測了跟蹤裝置俯仰方向實際位置和水平方向實際位置，在太陽系坐標中監測了太陽方位角和太陽高度角。

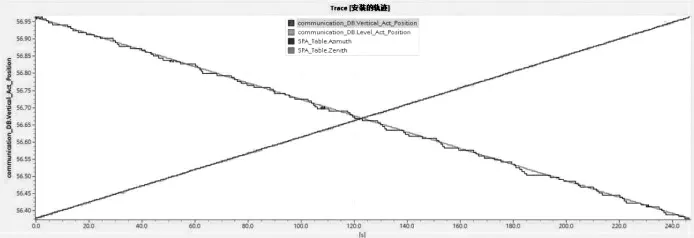
圖5 跟蹤裝置與太陽在某段時間內的跟蹤截圖

在線監測結果顯示：跟蹤裝置俯仰方向實際位置曲線與太陽高度角重合，說明裝置與太陽的高度角相一致。跟蹤裝置水平方向實際位置曲線與太陽方位角重合，說明裝置與太陽的方位角相一致。

4 結論

上述方法雖然使得跟蹤裝置實現了與太陽角度的對準，但是系統屬于開環狀態，此時需要借助外圍監測軟件通過串口接收安裝在跟蹤裝置上的光線傳感器反饋的數據,當軟件中紅色光斑移動到軟件界面定義的方格區域的幾何中心處時,跟蹤裝置的焦點、太陽和地心在一條直線上；說明光斑與集熱腔室就是完全重合的，由此證明，跟蹤裝置的零點確認是否準確直接關系到光斑與集熱腔體的對準。

如果零點確認不準，即便在控制系統和高精度的算法都成熟的條件下，跟蹤裝置也不能提高效率,達到其精準的隨動性，此時光熱轉換效率也就無從談起了。但引入該定零算法后，跟蹤精度更加精確、光熱效率顯著提升，進而提高了跟蹤裝置上發電機的工作效率，該算法還適用于其他高精度跟蹤的相關領域。