小水電智能微電網可靠性分析

邢智博，任家智，辛鑫，王永垚，劉子源

（山西能源學院，山西 太原 030001）

近年來，環境污染、能源稀缺等問題日益嚴峻，如何充分利用清潔能源成為業內人士研究的重點。智能微電網的出現，使能源利用率得到了大幅提高。作為由微電網、智能電網組合而成的全新電力系統，智能微電網可兼具孤島及并網模式，這也決定其可以對風能和光伏等常見能源進行充分利用。若將其用于偏遠地區，可以有效控制鋪設電纜的規模，降低項目投資費用。將其應用于城鎮地區，則能夠通過減輕用電負荷的方式有效提升大電網的穩定性。

1 研究背景

本文所研究的微電網可以拆分成光伏發電、儲能元件、小水電站和風力發電等部分，通常需要經由上述構件控制頻率電壓并提供無功/有功功率，這也決定了一旦設備出現故障，便有可能造成負荷停電。目前，可能造成負荷停電的情形主要包括以下幾種：一是分布式電源出現故障。故障發生后，通常需要花費數小時或數天進行維修方可恢復正常。二是電源受故障影響而跳機。此時需要工作人員重啟電源，重啟前重要負荷始終處于停電狀態，自動重啟的用時通常為數秒，而手動重啟的用時則會達到數小時。若出現無功/有功過載，將會使負荷大范圍波動，進而導致電源跳開。出現該問題后，既要重啟電源，同時還要甩負荷，兩項工作的耗時往往較重啟電源更長。三是由于電壓跌落或其他電能質量問題，致使設備跳機。經研究發現，開關動作、閃點以及故障均會造成電壓跌落，若分布式電源所接入的負荷較多，則需要頻繁開關，負荷可靠性也會受到影響［1］。

2 可靠性分析內容

微電網的本質是由負荷、分布能源和儲能裝置共同組成的發配電系統。智能電網則具有與供電網路相同的作用，即：以既有傳感器為依托，實時收集設備參數，向控制系統下達相應指令，由此達到對電力系統進行科學管理的目的［2］。要想使智能微電網所具有價值得到最大化實現，關鍵是要確保其性能優異且可靠，對微電網所具有的可靠性加以分析勢在必行。可靠性分析主要涉及安全性和充裕度兩方面的內容。對常規配電系統進行分析可知，雖然影響系統可靠性的因素較多，但充裕度的影響明顯強于其他因素，這是因為配電系統多采取鏈式運行模式，任一元件出現故障，均會造成供電中斷，進而給用戶工作或生活產生影響。對本文所討論的智能微電網而言，其可靠性主要取決于互聯系統，要想使系統得到穩定、可靠的運行，關鍵是要對動態問題進行深入分析，根據分布式電源的性能，評估系統可靠性。為保證分析所得出的結論具有實際意義，技術人員需要以可靠性計算所具有的特點為依據，創造性地引入負荷數據、等效動態模型等，希望在保證分析結果有效的前提下，有效降低分析難度。

3 可靠性分析過程及結果

本文所討論微電網由小水電、光伏和儲能等部分組成，對其可靠性加以評估所考慮的要素如圖1所示。

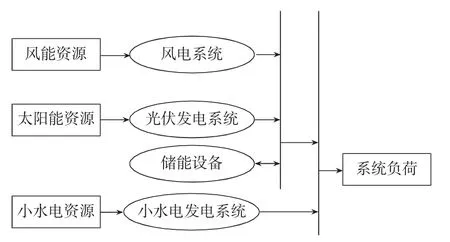
圖1 可靠性評估要素

考慮到在某些情況下，微電網與大電網的聯系并不緊密，因此，要想使微電網得到穩定且獨立的運行，關鍵是要接入小水電。其作用主要體現在兩個方面，一是為微電網持續供電，二是對儲能電站進行協調，使電力負荷和發電系統始終處于供需平衡的狀態［3］。

3.1 分析過程

3.1.1 建立模型

首先是建立小水電模型。實踐經驗表明，導致小水電停運的原因有兩個，分別是機組存在故障和水位高度不滿足要求，鑒于此，在建立相關模型時，為避免建模步驟過于復雜，技術人員決定將水位高度不滿足要求劃入機組故障的范圍。若將水輪機所搭載機組數量設定為n，將任一機組出現停運事故的概率設定為r，可以得到以下模型公式：

上式中，k代表停運機組總數，Pk代表累計停運概率。在0～1范圍內隨機抽取多組數據，對比所抽取數據和累計停運概率，就能夠準確掌握既有機組的狀態和可穩定運行機組的數量。隨后，針對機組運行情況、小水電出力情況所提出的要求為依據，參考狀態持續時長完成抽樣，便可以對小水電出力加以確定。

其次是建立裝置模型。評估光伏、儲能和風電可靠性的模型首選兩態模型，如圖2所示。

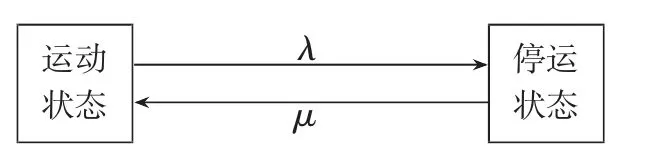
圖2 兩態模型

上圖中，λ 代表修復轉移率，μ 代表故障轉移率。技術人員可以憑借蒙特卡羅法，快速確定MTTF和MTTR取值［4］。考慮到狀態持續時長所對應抽樣值具有指數分布特征，可使用以下公式推算系統修復時長和無故障時長：

恒輪機床作為一家擁有120多年歷史的老牌德國機床企業，在如今全球，尤其是中國市場的制造業正處在轉型升級的時代中，依然保持著蓬勃的發展力及創造力。從數據上來看，恒輪機床在全球擁有超過2?000名員工，并且銷售業績也在持續地、穩固地上升，我們有理由相信，恒輪機床在經歷了超過100年的歷史后仍然是一家健康狀況十分良好的企業，而在產品創新方面也確實如此。

在上述公式中：MTTF代表無故障時長平均值；MTTR代表修復時長平均值；TTF代表無故障時長；TTR代表修復時長；U及U′均為隨機數，取值范圍是0～1。確定各項參數的取值后，便可以對強迫停運率進行計算，相關公式如下：

上式中，FOR代表強迫停運率。

最后是建立可靠性模型。在本文研究中，根據時序負荷情況建立了相應的模型，簡單來說，就是在年負荷最大值確定的前提下，使用百分數描述日負荷和周負荷的最大值。在上述工作結束后，便可以參考負荷峰值繪制出相應的年度負荷曲線，如圖3所示。

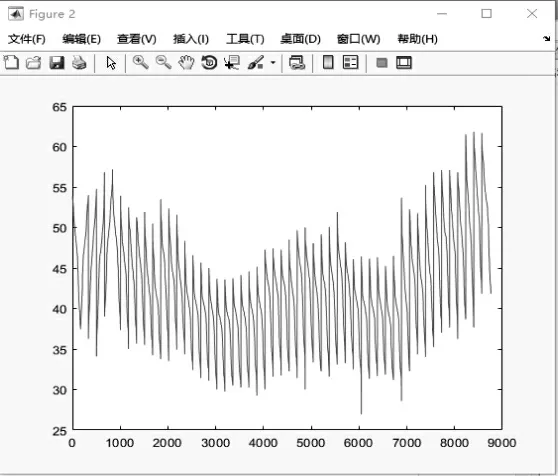
圖3 年度負荷曲線

對負荷曲線進行分析可知，全年負荷峰值出現在51周。如果將冬季作為一年的開端，冬季負荷明顯高于其他季節。如果將夏季作為一年的開端，則代表夏季負荷高于其他季節。要想快速、準確地計算出負荷期望值，應建立以下表達式：

在上式中，Plst（t）代表負荷期望值，Plmax代表年負荷最大值，Pweek（t）代表周負荷最大值與年負荷最大值之比，Pday（t）代表日負荷最大值與周負荷最大值之比，Phour（t）代表小時負荷最大值與日負荷最大值之比。

3.1.2 確定可靠性指標

對電力系統而言，其可靠性指標往往包括兩類，分別是概率指標和確定性指標，其中確定性指標難以對系統狀態進行全方位的表現，概率指標則不存在該問題［5］。鑒于此，本文選擇以系統和負荷為切入點，圍繞可靠性指標展開討論。

上述公式中：LOEE代表電源發電量與負荷需求不符時，微電網所期望的電量；ENSi代表各抽樣年中均無法達到負荷需求的實際電量；LOLE代表微電網對電源與負荷需求不符時間的期望；LLDi代表各抽樣年中存在電力不足問題的時長。隨后，技術人員便可以充分利用評估指標和已建立模型，對微電網各部分狀態進行判斷，并結合時序模擬分析所得到結果，確定微電網性能和既有負荷點是否可靠。

3.1.3 評估微電網可靠性

在本文研究中，依據蒙特卡羅法分析系統的可靠性，以小時為單位記錄系統電源運行參數和負荷變化情況。模擬總時長是365天，時間的間隔是1h，具體流程如下：第一步，以年為單位，獲取小水電、光伏以及負荷的相關數據，生成相應的出力時序；第二步，以既有模型為基礎，使用現有公式推算電源的狀態時序；第三步，根據狀態時序、出力時序，對功率輸出時序加以確定；第四步，對比負荷需求、電源出力情況，對LOEE、LOLE取值進行計算，參考相應的經濟指標，得出最終結論。評估流程如圖4所示。

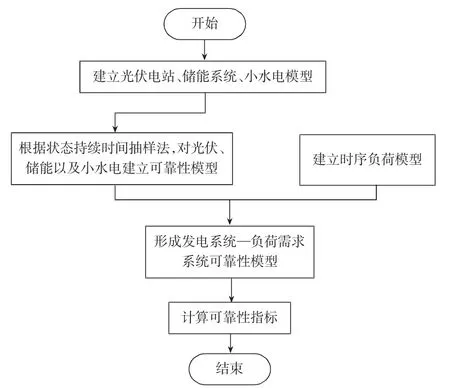
圖4 評估流程

3.2 分析結果

3.2.1 負荷峰值與可靠性的關系

本文所研究智能微電網搭載有相應的發電系統，系統可靠性極易被負荷波動所影響。對負荷峰值、系統可靠性之間的關系進行分析，能夠準確掌握系統所能承受負荷的最大值，便于工作人員以微電網所展示的狀態為依據，對后續運行方案及策略加以調整，使發電系統以及微電網始終處于穩定、高效的運行狀態。研究發現，負荷峰值在60kW以下時，各項可靠性指標相對穩定，這表示發電系統與負荷需求相符；負荷峰值超過60kW后，各項指標均會發生明顯的變化，換言之，要想使系統得到穩定且高效的運行，關鍵是要保證負荷值不超過60kW。

3.2.2 水庫容量與可靠性的關系

基于評估可靠性的模型模擬微電網所搭載電力系統，可以得到以下數據：首先，每組水電機組的容量都是30MW；其次，水庫原始水量能夠達到其容量的95%～97%；最后，結合某地所提供統計數據可知，水體徑流量的平均值在0.32m2/s左右，由此可見，水流量與水電機組所提出需求相符，這表示水流量可以維持水電機組穩定運行。微電網元件故障情況統計表見表1。

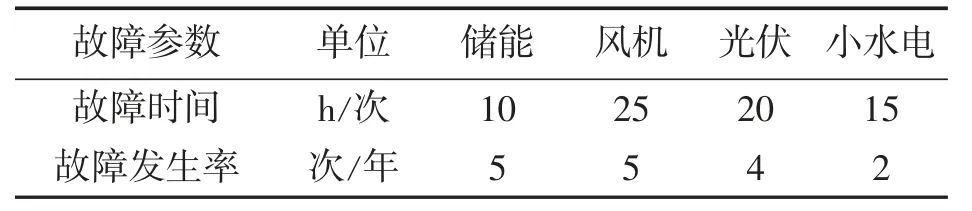
表1 微電網元件故障情況統計表

隨后，本文圍繞水庫容積、系統可靠性之間的關系展開了研究。通過模擬不同容積的水庫，判斷容積給可靠性指標所產生的影響。經過分析發現，在負荷確定、上游水量確定的前提下，水庫蓄水量會隨著容積的增大而增多，與此同時，LOEE、LOLE的取值均會有所下降。水庫容積增大到15萬m3后，蓄水量差值將處于相對穩定的狀態，LOEE、LOLE的下降速度有所減慢，并逐漸趨于平緩，同時既有水資源的利用率也較以往有所提高。由此可見，對本項目而言，要想使系統具有良好的可靠性，關鍵是要將水庫容積控制在約15萬m3。

4 結論

本文分別對儲能、小水電、風電及光伏模型進行了建立，并以所建立的模型為依托，根據電源所展示的運行狀態，圍繞峰值負荷、水庫容積與系統可靠性之間的關系展開了討論。本文研究所得結論如下：第一，峰值負荷與系統可靠性密切相關，要想使本系統得到穩定運行，應保證峰值負荷始終不超過60kW；第二，水庫容積同樣會給系統可靠性產生影響，酌情增大水庫容積，既能夠使系統更加可靠，又可以為項目的經濟價值提供保證，但若水庫容積增大過多，會給可靠性造成負面影響。