地震作用下分層土邊坡多滑面變形破壞的數值模擬研究

宋健 陸朱汐 謝華威 吳凱莉

摘要：

地震引起的滑坡對生命、環境和經濟造成了巨大的威脅。目前，對于地震作用下邊坡穩定性的研究主要集中在單一滑動面破壞模式，對于具有多個潛在滑動面邊坡的地震穩定性研究比較欠缺。基于此，利用有限差分軟件FLAC對不同邊坡進行地震穩定性數值模擬，對比分析不同強度地震動作用下均質土體、分層土體和含軟弱夾層土體邊坡的滑動面演化過程和永久變形分布特征。結果表明：對于均質邊坡，地震引起的滑動面為單一的整體滑動面，地震動強度的增加僅導致沿滑動面的永久變形量增大;對于非均質邊坡，在地震作用下還可能形成通過土層交界面的局部滑動變形，且地震作用下最先形成和發生變形的滑動面與靜力條件下得到的最小安全系數對應的最危險滑動面一致;同時，地震引起的邊坡淺層和深層變形破壞存在復雜的相互影響，當局部淺層滑動先發生時，地震動的進一步增大很容易誘發更深層的坡體滑動，而當深層滑動先發生時，由于塑性變形影響地震慣性力向上部坡體的傳播，淺層坡體的進一步滑動變形相對較難被觸發。

關鍵詞：

地震邊坡穩定性; 數值模擬; 滑動面; 變形破壞

中圖分類號： TU43????? 文獻標志碼：A?? 文章編號： 1000-0844（2023）02-0296-10

DOI：10.20000/j.1000-0844.20210812002

Numerical study of the deformation and failure of layered soil

slopes with multiple sliding surfaces under earthquakes

SONG Jian1，2， LU Zhuxi2， XIE Huawei2， WU Kaili2

（1.Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering，

Hohai University， Nanjing 210000， Jiangsu， China;

2.College of Civil Engineering and Transportation， Hohai University， Nanjing 210000， Jiangsu， China）

Abstract：

Landslides caused by earthquakes pose a great threat to life， the environment， and the economy. Present studies on slope stability under earthquakes mainly focus on the failure modes of single sliding surfaces， while studies on slope stability with multiple potential sliding surfaces are comparatively obscure. A numerical simulation is conducted on the seismic stability of different slopes by using the finite difference software FLAC. The evolution process of sliding surfaces and the distribution characteristics of permanent deformation of homogeneous soil slopes， layered soil slopes， and soil slopes with weak interlayers under different earthquake intensities are compared and analyzed. Results reveal that the sliding surface of homogeneous slopes caused by earthquakes exhibits a single sliding surface， and the increase in seismic intensity only leads to an increase in permanent deformation along the sliding surface. For heterogeneous slopes， seismic action may also trigger local sliding deformation at the soil interface， and the sliding surface initially formed under seismic action is consistent with the most dangerous sliding surface corresponding to the minimum safety factor obtained under static conditions. In addition， a complex interaction exists between the shallow and deep slope deformations and failures caused by earthquakes. If the shallow sliding occurs first， further increase in ground motion can easily induces deep slope sliding; if the deep sliding occurs first， then plastic deformation affects the propagation of seismic inertia force to the upper slope body; thus， the further sliding deformation of the shallow slope is relatively difficult to trigger.

Keywords：

seismic slope stability; numerical simulation; sliding surface; deformation and failure

0 引言

邊坡穩定性是巖土工程領域研究的重要課題。尤其在強烈地震作用下，邊坡極易發生失穩，對生命、環境和經濟都會造成巨大的威脅［1］。

目前，對地震邊坡穩定性分析常用的研究方法有擬靜力方法、Newmark滑塊分析法和數值分析方法。擬靜力方法是將地震引起的動荷載簡化為作用在邊坡上的慣性力。但在地震的過程中，地震動時刻發生著變化，不能簡單地用某一時刻的安全系數去評判地震動期間邊坡的穩定性。Newmark滑塊分析法是將地震滑坡簡化為一個坡體滑塊沿著滑動面的滑動問題［2］，考慮地震動的時程變化，用邊坡永久位移來評判邊坡的穩定性。但Newmark滑塊分析法存在著模型過于簡化，不能考慮復雜的土體應力應變關系等缺陷［3］。相較于前兩種方法，數值分析方法能考慮復雜的應力與應變關系，且能夠比較真實地反映實際邊坡模型的滑動面形成和破壞機理。同時，數值分析方法在分析邊坡穩定性時可以模擬復雜的地質條件和荷載工況，可獲得計算模型任意時步、任意位置的應力、應變和位移等信息，分析邊坡的變形特征和漸進性破壞過程［4］。

許多實際的滑坡并非只有單一滑動面，在外部荷載擾動下，可能會產生多個滑動面［5］。例如新灘斜坡在下伏基巖面發生整體下滑的同時，坡體的上層還產生二次平行滑移，即產生雙層滑移［6］。在靜力作用下邊坡多滑面失穩的研究中，楊濤等［7-8］以傳遞系數法為基礎，討論了考慮上層滑面影響的各層滑面穩定性的計算和各層滑體的滑坡推力計算及其分布形式的確定，同時開展了大型地質力學模型試驗，模擬了邊坡的開挖過程，分析了多級多層復合滑坡的變形失穩機制和工程病害及相應抗滑支擋結構的加固效果;陳力華等［9］基于塑性力學上限定理，提出了一種能考慮多滑動面之間相互作用的邊坡穩定性分析方法;張海寬等［10］基于統一強度理論研究了多層滑坡體中抗滑樁的最大樁間距;鄭智洋等［11］基于傳統強度折減法和土體抗剪切作用的差異性提出一種雙折減系數法用以評價多滑面的穩定性；龍建輝等［12］研究了雙層軟弱夾層順層巖質邊坡，考慮軟弱夾層的抗剪強度在滑坡不同發育階段的強度衰減，分析了滑坡過程中不同滑面的相互影響。

上述研究針對靜力條件下的多滑面邊坡穩定性分析，而在地震作用下，復雜土層邊坡也有可能發生多滑面破壞，且地震作用下多滑面滑坡的動力響應與變形耦合機理更為復雜。Wartman等［13］和艾揮等［14］通過邊坡地震變形的振動臺模擬試驗，表明了在地震作用下邊坡可能產生多個破壞滑動面;Leshchinsky等［15］提出了嵌套Newmark模型以考慮多滑面滑坡的情況，該方法將邊坡離散成一系列的嵌套滑塊，分別計算每個滑塊的滑動位移，從而得到邊坡的最終滑移，但該方法忽略了各滑塊體之間滑動時的相互作用;Song等［16-17］提出了一種考慮地震多滑面耦合滑移的Newmark滑塊分析法，并考慮了坡體滑移和土層動力響應的相互影響。

目前，地震作用下的邊坡多滑面破壞研究相對較少，且主要基于Newmark理論方法分析不同滑面的地震永久變形量，對復雜滑面系統的形成和破壞機理還沒有深入認識。本文利用有限差分軟件FLAC，對地震作用下分層土邊坡的多滑動面演化和變形特征進行深入研究，基于非線性彈塑性土體本構模型，探究了均質、分層、含軟弱夾層土體簡化邊坡在地震動下坡體的塑性剪應變增量和滑坡體的永久位移發展過程。文中的數值模擬研究結果對深入認識地震動引起的邊坡淺層和深層耦合變形破壞模式提供了參考。

1 分層土簡化邊坡數值模型的建立

1.1 邊坡模型

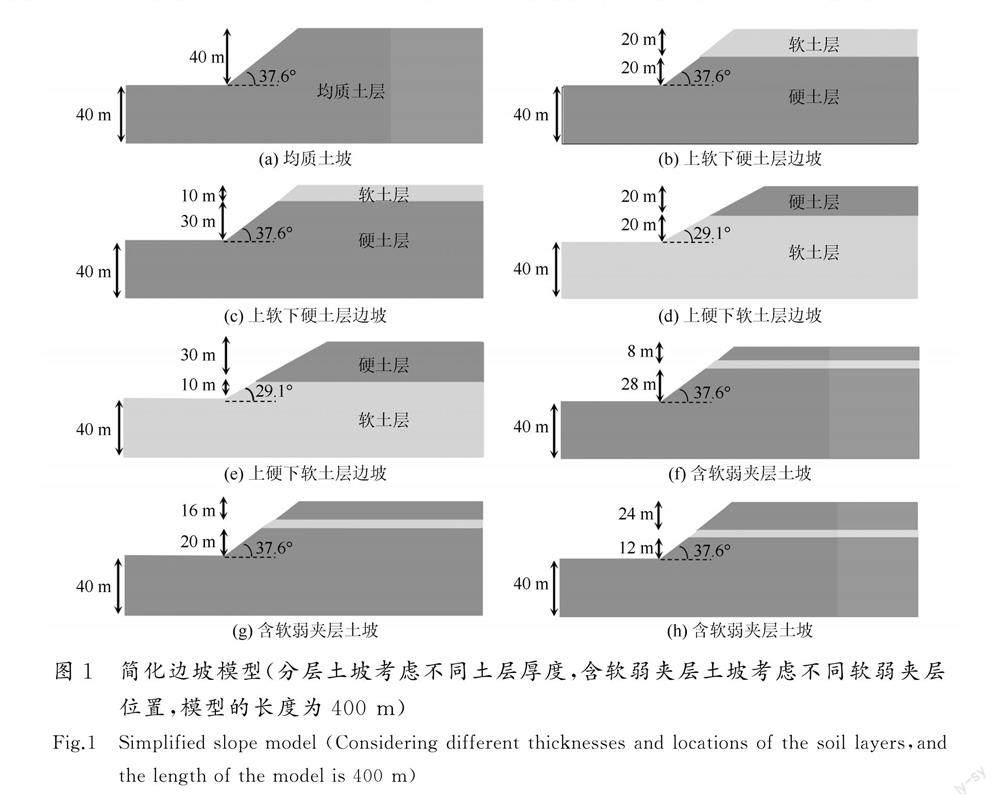
由于地質構造運動、沉積等原因，土坡坡體的材料往往由多層物理力學性質差異較大的土體組成，其分層界面可能會控制邊坡的滑動面位置和失穩模式。本文選用上軟下硬、上硬下軟和含軟弱夾層的水平分層土體邊坡模型為研究對象，這三種分層土邊坡代表了實際分層邊坡的不同土層結構［18］，同時，水平分層土體邊坡模型也在以往的研究中廣泛采用［18-22］。分別建立均質土層邊坡、分層土體邊坡和含軟弱夾層土體邊坡，邊坡高度均取為40 m，土層深度為80 m，土層底部為基巖。為保證邊坡在靜力條件下處于穩定狀態，不同土層結構的邊坡取不同的坡角。同時，為盡量減小動力分析中地震波在兩側邊界處反射的影響，邊坡模型取400 m長（10倍邊坡高度）。第一類為均質邊坡，邊坡由硬土層組成，坡角為37.6°，邊坡模型和尺寸如圖1（a）所示。第二類為分層土邊坡，分層土邊坡分為兩類模型，分別為上軟下硬土層邊坡和上硬下軟土層邊坡，上軟下硬土層邊坡的坡角為37.6°，上硬下軟土層邊坡的坡角為29.1°；同時，為了研究不同上覆土層厚度的邊坡動力響應，模型分為上覆20 m厚軟土和上覆10 m厚軟土的上軟下硬邊坡;與上軟下硬邊坡類似，上硬下軟邊坡分為上覆20 m厚硬土層和上覆30 m厚硬土層的上硬下軟邊坡;分層土邊坡模型和尺寸如圖1（b）～（e）所示。第三類為含有軟弱夾層的邊坡，邊坡由硬土層組成，軟弱夾層由軟土層組成，考慮夾層位置位于邊坡不同高度，共建立三個模型，分別為軟弱夾層距坡頂8 m、16 m、24 m的邊坡模型。軟弱夾層厚度為4 m，邊坡坡角為37.6°，邊坡模型和尺寸如圖1（f）～（h）所示。

1.2 土體參數

土體基于非線性彈塑性本構模型，動力分析時采用滯后阻尼和瑞利阻尼相結合的形式。滯后阻尼采用FLAC內置的黏土的default模型［23］描述土體剪切模量隨剪應變增大的非線性衰減規律，土體塑性行為采用莫爾-庫倫模型描述。瑞利阻尼采用剛度相關的瑞利阻尼形式，以避免地震波的高頻成分被過于放大。土體瑞利阻尼的最小臨界阻尼比均取值為0.5%，中心頻率根據不同的邊坡模型的一階和二階自振頻率進行選取［23-24］。軟土層和硬土層土體的物理力學參數和滯后阻尼參數列于表1。

1.3 地震動輸入及邊界條件

研究采用的地震動從美國太平洋地震工程研究中心的NGA West2地震動數據庫中選取，為1994年美國加州北嶺6.7級（矩震級）中記錄的地震動，記錄臺站為Pacoima 大壩下游臺站。采用方位角為175°的水平分量地震動作為輸入。此地震動記錄臺站場地為出露基巖，上覆30 m深度基巖平均剪切波速為2 016 m/s。地震動加速度時程及加速度的傅里葉譜曲線如圖2所示，地震動峰值加速度為PGA=0.41g，主導頻率在2 Hz左右。

在靜力分析時，模型邊界條件為側邊界的水平方向固定、底部邊界的水平和豎直方向固定;動力分析時，因為選取了記錄于基巖場地的地震動數據，故模型底部為基巖，輸入加速度時程，側邊界為自由場邊界。基于圖2（b），考慮地震動包含的最大頻率為20 Hz，則在軟土層中傳播的最小波長為10 m，在硬土層中傳播的最小波長為20 m。因此，為了保證地震波20 Hz以下頻率分量在土層中的準確傳播，將土體的網格尺寸取為1/10的最小波長，軟土層的網格尺寸取為1 m，硬土層的網格尺寸取為2 m。

模型建立后，首先獲取邊坡初始自重應力場，達到平衡狀態，進行靜力分析;然后施加地震動，進行邊坡動力響應分析。

2 分層邊坡的地震滑動面演化和變形分析

2.1 均質邊坡

首先對均質土坡進行分析，作為后續分層土坡的地震變形和破壞模式分析的對比案例。基于FLAC內置強度折減法，計算得到均質邊坡最小安全系數為1.09。圖3為對應于最小安全系數的臨界滑動面位置，采用剪應變增量分布表征。可以看出，邊坡滑動面為通過坡腳的整體滑動，在邊坡初始自重應力條件的基礎上，進行邊坡動力響應分析。將地震動進行縮放得到不同強度的地震動時程作為輸入，計算得到的邊坡最終剪應變增量分布如圖4所示。可以看出，在地震動較小的情況下（0.1倍地震動），邊坡塑性滑動區從坡腳開始形成，逐漸向坡頂延伸，邊坡永久位移量較小（最大僅為0.027 m）。

當地震動強度增大時，塑性滑動區將貫穿坡體形成完整的滑動面，邊坡最大永久位移量由0.779 m（原始地震動）增大至1.841 m（2倍地震動）。值得指出的是，對于均質邊坡，在地震動作用下和靜力條件下均為單一滑動面，地震動強度的增大僅僅導致永久變形量的增大。

為了進一步揭示地震動作用下邊坡滑動面的演化情況，圖5給出了均質邊坡在原始地震動作用下不同時刻的剪應變增量云圖。可以看出，在地震動作用3 s后，邊坡塑性滑動區從坡腳開始形成，當地震動作用6 s后，邊坡剪應變增量的量級已較大，塑性滑動區已完全貫通。從圖2（a）也可以看出，地震動強度最大部分主要集中在3～5 s的時間段內。

2.2 分層邊坡

2.2.1 上軟下硬土層邊坡

對于上覆軟土厚度為20 m的上軟下硬邊坡［圖1（b）］，靜力下計算得到上軟下硬邊坡的最小安全系數為1.03。與均質邊坡不同，上軟下硬邊坡最小安全系數對應的臨界滑動面通過坡面，滑出口位置在軟土層和硬土層交界面處（圖6）。

計算得到不同強度地震動作用下的邊坡最終剪應變增量分布及永久位移場如圖7、圖8所示。對比均質邊坡，在地震動強度較小時，邊坡動力分析得到的滑動面僅穿過上覆軟土層，永久位移場也主要集中在上覆土層，最大位移量為0.29 m。而當地震動強度增大為原始地震動時，邊坡形成了第二滑動面，為通過坡腳的深層滑面。此時邊坡永久位移場分布在整個深層滑動體內，最大位移量為1.661 m。

圖9通過給出上軟下硬土層邊坡在原始地震動作用1 s、3 s、3.5 s和6 s后的剪應變增量云圖，描述了滑動面的演化過程。與均質邊坡不同，在地震動作用1s后，該分層邊坡塑性滑動區即從土層界面處逐漸形成;當地震動作用3 s后，邊坡塑性滑動區擴展至整個上覆土層內;當地震動作用3.5 s后，第二塑性滑動區從坡腳開始形成;當地震動作用6 s后，深層滑動面完全貫通。圖10給出了上軟下硬土層邊坡在不同強度地震動作用下的坡面水平永久位移隨高度的變化結果。圖中SF為地震動縮放因子，是指在原始地震動強度的基礎上進行縮小或放大，例如0.1為縮小0.1倍，反之2即放大2倍。可以看出，與均質邊坡的整體滑動不同，在較小的地震動作用下，分層邊坡土體滑動僅發生在上覆軟土層底部，而當地震動較大時，分層邊坡土體在淺層和深層均產生滑動。

因此，對于上軟下硬邊坡，在實際地震動荷載作用下，邊坡可能同時發生淺層和深層破壞。由于邊坡淺層和深層破壞的滑動體體積相差較大，坡體失穩滑動造成的災害水平也完全不同，因而需要對地震作用下邊坡多層滑動失穩破壞進行準確的評價，且邊坡淺層和深層之間存在相互作用，這是由于多個滑體滑動時，深層滑體滑動的發生將影響地震慣性力在坡體內的傳遞，因此不同滑體也會相互影響。

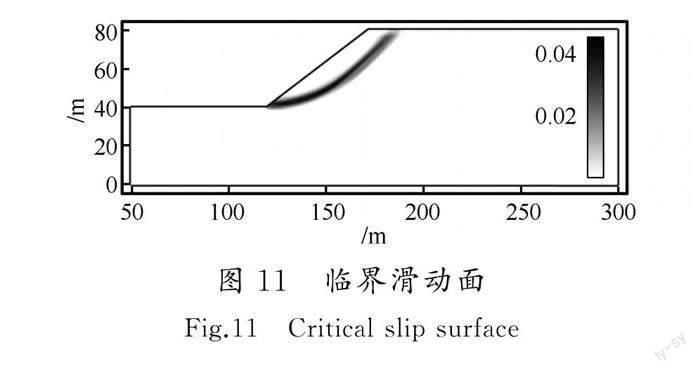
改變上覆土體厚度，由20 m厚軟土改為10 m厚軟土［圖1（c）］。通過靜力分析計算得到邊坡最小安全系數為1.08。從圖11的臨界滑動面位置可以看出，當上覆軟土層厚度由20 m減小至10 m時，最小安全系數對應的滑動面由軟土層內的局部滑動轉變為通過坡腳的整體滑動。因此，分層土體邊坡的潛在滑動面位置將受土體強度參數和土層厚度共同影響。

計算得到不同強度地震動作用下的坡面水平永久位移隨高度的變化結果如圖12所示。在原始地震動作用下，該邊坡與均質邊坡類似，僅產生整體滑動面，當地震動放大兩倍時，邊坡仍以整體滑動為主，但在淺層坡體局部出現了部分塑性滑動區域，淺層滑動面位置節點相對水平位移為0.066 m。相對水平位移量較小的原因可能是深層滑動面先發生了較大的永久變形，對地震慣性力向坡體上部傳播造成一定削弱效應。

2.2.2 上硬下軟土層邊坡

對于上覆硬土厚度20 m的上硬下軟邊坡［圖1（d）］，通過靜力分析計算得到上硬下軟邊坡最小安全系數為1.02，對應的最危險滑動面為通過坡腳的整體滑動，如圖13所示。

圖14是上硬下軟土層邊坡在不同強度地震動作用下的坡面水平永久位移隨高度的變化結果。可以看出，在不同強度地震動作用下，上硬下軟邊坡與均質邊坡類似，土體滑動僅發生在邊坡底部。雖然邊坡存在硬土層與軟土層的強度分界面，但滑動并未在界面處發生。這可能是由于上覆硬土層強度較大，導致局部滑動的屈服加速度遠大于整體滑動的屈服加速度，同時，深層滑動的發生也阻礙了地震波慣性力的傳遞。因此，對于上硬下軟土層邊坡，在不同強度地震動作用下均只形成一個整體滑動面。

與上覆20 m厚硬土的邊坡相比，上覆30 m厚的硬土邊坡［圖1（e）］靜力分析計算得到邊坡最小安全系數增大為1.06，對應的最危險滑動面仍然為通過坡腳的整體滑動（圖15）。

坡面水平永久位移隨高度的變化結果如圖16所示。可以看出，在不同強度地震動作用下，土體滑動仍然僅發生在邊坡底部。上覆硬土層厚度的增加雖然沒有形成第二滑動面，但在強度較大的地震動作用下，水平永久位移在土層界面位置出現了拐點（SF為2時，該處相對水平位移為0.022 m）。由于上覆硬土層厚度增大，導致整體滑動的屈服加速度增大而局部滑動的屈服加速度減小。雖然在局部潛在滑動面位置發生了一定的相對位移，但在深層滑動先發生的條件下很難持續發展。

2.3 含軟弱夾層邊坡

軟弱夾層在巖質邊坡中非常常見，但在土質邊坡中也經常存在。諸多學者針對含軟弱夾層土坡的穩定性進行了研究［18-20，25-26］，其中有不少含軟弱夾層土坡的工程案例，如京珠高速長沙—湘潭段的含軟弱夾層土質邊坡［25］、三峽庫區含軟弱夾層土坡［26］等。因而，含軟弱夾層土坡的靜動力穩定性存在研究的必要性。

通過對含軟弱夾層邊坡的靜力分析計算，得到軟弱夾層距坡頂8 m、16 m、24 m的邊坡的最小安全系數分別為1.07、1.06和1.05［圖1（f）～（h）］，即軟弱夾層位置越深，邊坡安全系數越小。圖17分別為軟弱夾層距坡頂8 m、16 m、24 m的邊坡臨界滑動面，對比均質邊坡，對于軟弱夾層距離坡頂8 m和16 m的邊坡，最危險滑動面仍為通過坡腳的整體滑動，而當軟弱夾層位于更深位置時（24 m），最危險滑動面為穿過軟弱夾層的局部滑動。顯然，軟弱夾層的存在降低邊坡的安全系數，且其位置越深，邊坡越容易在軟弱夾層處發生局部滑動。

在邊坡初始自重應力條件的基礎上，進行邊坡動力響應分析。對比均質邊坡的整體滑動，軟弱夾層位于8 m深處的邊坡以整體滑動為主，但在淺層軟弱夾層的位置處，坡體局部出現了部分塑性滑動區域。從圖18該邊坡的坡面水平永久位移隨高度變化結果可看出，在坡腳附近發生了較大的滑移，而在原始地震動作用下，淺層滑動面位置節點相對水平位移為0.047 m，當地震動放大至兩倍時，節點相對水平位移增大至0.117 m。由于深層滑動面先發生的永久變形影響了地震慣性力的傳遞，因此即使較大的地震動也沒有導致淺層滑面發生大的滑移。

隨著軟弱夾層深度的進一步增加，通過軟弱夾層的局部滑動面和通過坡腳的整體滑動面的剪應變增量也大大增加，局部滑動的位移場比邊坡整體滑動更加明顯。從圖19、圖20可以看出，當軟弱夾層深度增大至24 m時，淺層滑動面先形成并產生永久變形，深層滑動面在后續更強的地震荷載作用下被進一步誘發。

3 結論

本文采用數值模擬方法，基于非線性彈塑性土體本構模型，揭示了地震作用下不同土層結構邊坡的滑動面形成過程及演化機理，證明了地震動荷載可能引起分層土邊坡的多滑動面失穩破壞模式，得到結論如下：

（1） 對于均質邊坡，地震引起的滑動面為單一的整體滑動面，地震動強度的增大僅僅導致沿滑動面的永久變形量的增大，而由于非均質邊坡在土層交界面存在強度不連續界面，在地震作用下可能形成通過土層界面的局部滑動以及坡底的深層整體滑動;

（2） 地震作用下最先形成和發生滑動位移的滑動面與靜力條件下得到的最小安全系數對應的最危險滑動面（臨界滑動面）較為一致;

（3） 地震引起的邊坡淺層和深層變形破壞存在復雜的相互影響，當淺層局部滑動先發生時，地震動的進一步增大很容易誘發更深層的坡體滑動，而當深層滑動先發生時，淺層坡體的進一步滑動相對較難被完全觸發，主要是由于深層滑動阻礙了地震慣性力在上部坡體的傳遞。

參考文獻（References）

［1］ 邢愛國，吳志堅，陳龍珠，等.汶川地震在甘肅省的次生典型邊坡災害特征［J］.西北地震學報，2010，32（1）：95-98.

XING Aiguo，WU Zhijian，CHEN Longzhu，et al.Characteristics of secondary typical slope disaster in Gansu Province induced by the Wenchuan earthquake［J］.Northwestern Seismological Journal，2010，32（1）：95-98.

［2］ NEWMARK N M.Effects of earthquakes on dams and embankments［J］.Géotechnique，1965，15（2）：139-160.

［3］ 劉愛娟，鄭路，劉鐵新，等.考慮動態臨界加速度的地震邊坡永久位移研究［J］.地震工程學報，2017，39（5）：876-882.

LIU Aijuan，ZHENG Lu，LIU Tiexin，et al.Study of seismic slope permanent displacements with dynamic critical acceleration［J］.China Earthquake Engineering Journal，2017，39（5）：876-882.

［4］ 高玉峰，王迪，張飛.三維土質邊坡穩定性分析方法研究現狀與展望［J］.河海大學學報（自然科學版），2015，43（5）：456-464.

GAO Yufeng，WANG Di，ZHANG Fei.Current research and prospects of 3D earth slope stability analysis methods［J］.Journal of Hohai University （Natural Sciences），2015，43（5）：456-464.

［5］ 張家明.含軟弱夾層巖質邊坡穩定性研究現狀及發展趨勢［J］.工程地質學報，2020，28（3）：626-638.

ZHANG Jiaming.State of art and trends of rock slope stability with soft interlayer［J］.Journal of Engineering Geology，2020，28（3）：626-638.

［6］ 賀可強.大型坡積層斜坡的雙層滑移模型與雙層滑移規律：以新灘滑坡分析為例［J］.河北地質學院學報，1992，15（1）：51-59.

HE Keqiang.A double-sliding model of large scale sliderock slope and its double-sliding law—setecting Xintan landslide as analysing example［J］.Journal of Hebei GEO University，1992，15（1）：51-59.

［7］ 楊濤，周德培，羅陽明.考慮層間作用的多層滑坡分析方法［J］.巖石力學與工程學報，2005，24（7）：1129-1133.

YANG Tao，ZHOU Depei，LUO Yangming.A new method considering inter-layer interactions for analysis of multi-layers landslides［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（7）：1129-1133.

［8］ 楊濤，周德培，周應華，等.多級多層復合滑坡工程病害的試驗研究［J］.工程地質學報，2005，13（3）：325-329.

YANG Tao，ZHOU Depei，ZHOU Yinghua，et al.Experimental study of engineering slope hazards of multi-layer and multi-level landslides［J］.Journal of Engineering Geology，2005，13（3）：325-329.

［9］ 陳力華，靳曉光，劉新榮，等.多滑面滑坡穩定性分析［J］.地下空間與工程學報，2008，4（6）：1138-1141.

CHEN Lihua，JIN Xiaoguang，LIU Xinrong，et al.Stability analysis of landslides with multi slip surface［J］.Chinese Journal of Underground Space and Engineering，2008，4（6）：1138-1141.

［10］ 張海寬，張友，劉濤，等.基于統一強度理論多層滑坡體中抗滑樁最大樁間距研究［J］.地質科技情報，2017，36（5）：209-215.

ZHANG Haikuan，ZHANG You，LIU Tao，et al.Maximum pile spacing of stabilizing piles in multilayer sliding mass based on unified strength theory［J］.Geological Science and Technology Information，2017，36（5）：209-215.

［11］ 鄭智洋，蘇培東，劉波，等.基于雙折減系數法的多滑面邊坡穩定性分析方法研究［C］//中國地質學會.2018年全國工程地質學術年會論文集.北京：《工程地質學報》編輯部，2018：108-115.

ZHENG Zhiyang，SU Peidong，LIU Bo，et al.Study on the stability analysis of multi-slip side slope based on double reduction method［C］//Chinese Geological Society.Proceedings of the National Engineering Geology Annual Conference in 2018.Beijing：Editorial Department of Journal of Engineering Geology，2018：108-115.

［12］ 龍建輝，任杰，曾凡桂，等.雙軟弱夾層巖質滑坡的滑動模式及變形規律［J］.煤炭學報，2019，44（10）：3031-3040.

LONG Jianhui，REN Jie，ZENG Fangui，et al.Sliding mode and deformation law of double weak interlayer rock landslide［J］.Journal of China Coal Society，2019，44（10）：3031-3040.

［13］ WARTMAN J，SEED R B，BRAY J D.Shaking table modeling of seismically induced deformations in slopes［J］.Journal of Geotechnical and Geoenvironmental Engineering，2005，131（5）：610-622.

［14］ 艾揮，吳紅剛，馮文強，等.多滑動面滑坡變形破壞機理的振動臺試驗研究［J］.防災減災工程學報，2018，38（1）：65-71.

AI Hui，WU Honggang，FENG Wenqiang，et al.Shaking table test study on deformation and failure mechanism of landslide with multiple slip surface［J］.Journal of Disaster Prevention and Mitigation Engineering，2018，38（1）：65-71.

［15］ LESHCHINSKY B A.Nested Newmark model to calculate the post-earthquake profile of slopes［J］.Engineering Geology，2018，233：139-145.

［16］ SONG J，FAN Q Q，FENG T G，et al.A multi-block sliding approach to calculate the permanent seismic displacement of slopes［J］.Engineering Geology，2019，255：48-58.

［17］ SONG J，WU K L，FENG T G，et al.Coupled analysis of earthquake-induced permanent deformations at shallow and deep failure planes of slopes［J］.Engineering Geology，2020，274：105688.

［18］ 李亮，鄧東平，趙煉恒.基于滑動面搜索的分層土坡穩定性分析新方法［J］.中南大學學報（自然科學版），2012，43（10）：3995-4002.

LI Liang，DENG Dongping，ZHAO Lianheng.A new method for stability analysis of layered slopes based on search of sliding surface［J］.Journal of Central South University （Science and Technology），2012，43（10）：3995-4002.

［19］ 黃茂松，王浩然，劉怡林.基于轉動-平動組合破壞機構的含軟弱夾層土坡降雨入滲穩定上限分析［J］.巖土工程學報，2012，34（9）：1561-1567.

HUANG Maosong，WANG Haoran，LIU Yilin.Rotation-translation combined mechanism for stability analysis of slopes with weak interlayer under rainfall condition［J］.Chinese Journal of Geotechnical Engineering，2012，34（9）：1561-1567.

［20］ 王睿，張嘎，張建民.降雨條件下含軟弱夾層土坡的離心模型試驗研究［J］.巖土工程學報，2010，32（10）：1582-1587.

WANG Rui，ZHANG Ga，ZHANG Jianmin.Centrifuge modeling of rainfall-induced deformation of slopes with weak layers［J］.Chinese Journal of Geotechnical Engineering，2010，32（10）：1582-1587.

［21］ 姬建，王樂沛，廖文旺，等.基于WUS概率密度權重法的邊坡穩定系統可靠度分析［J］.巖土工程學報，2021，43（8）：1492-1501.

JI Jian，WANG Lepei，LIAO Wenwang，et al.System reliability analysis of slopes based on weighted uniform simulation method［J］.Chinese Journal of Geotechnical Engineering，2021，43（8）：1492-1501.

［22］ DING Y，WANG G，YANG F.Parametric investigation on the effect of near-surface soil properties on the topographic amplification of ground motions［J］.Engineering Geology，2020：105687.

［23］ ITASCA Consulting Group.FLAC-fast Lagrangian analysis of continua，version 5.0［R］.Minneapolis：ITASCA Consulting Group，Incorporated，2005.

［24］ MNICA M，OVANDO E，BOTERO E.Assessment of damping models in FLAC［J］.Computers and Geotechnics，2014，59：12-20.

［25］ 何忠明，王保林，胡慶國，等.強降雨條件下含軟弱夾層土坡穩定性影響因素敏感性分析［J］.長沙理工大學學報（自然科學版），2017，14（3）：21-28.

HE Zhongming，WANG Baolin，HU Qingguo，et al.Sensitivity analysis of factors influencing stability of soil slope with soft interlayer under heavy rainfall conditions［J］.Journal of Changsha University of Science & Technology （Natural Science），2017，14（3）：21-28.

［26］ 劉濤，張海寬，張友，等.三維復合多層滑坡體中抗滑樁最小樁間距研究［J］.巖石力學與工程學報，2018，37（2）：473-484.

LIU Tao，ZHANG Haikuan，ZHANG You，et al.Minimum pile spacing between stabilizing piles in 3D composite multilayer landslide［J］.Chinese Journal of Rock Mechanics and Engineering，2018，37（2）：473-484.