變時(shí)滯反饋控制的混合中立型隨機(jī)延遲微分方程的指數(shù)穩(wěn)定性

劉 琪 蘭光強(qiáng)

(北京化工大學(xué) 數(shù)理學(xué)院, 北京 100029)

引 言

帶有變時(shí)滯反饋控制的混合中立型隨機(jī)延遲微分方程(HNSDDEs)常被用于系統(tǒng)未來(lái)的建模,目前已經(jīng)被廣泛應(yīng)用于種群生態(tài)、神經(jīng)網(wǎng)絡(luò)以及激光器動(dòng)力學(xué)等領(lǐng)域。

對(duì)于隨機(jī)系統(tǒng)突然性的結(jié)構(gòu)變化,常采用連續(xù)時(shí)間馬氏鏈來(lái)描述,帶有馬氏鏈的隨機(jī)延遲微分方程即為混合隨機(jī)延遲微分方程。 文獻(xiàn)[1]具體研究了混合隨機(jī)延遲微分方程,文獻(xiàn)[2 -4]則進(jìn)一步考慮了其穩(wěn)定性及有界性,文獻(xiàn)[5 -7]又?jǐn)U展到了帶中立項(xiàng)的混合隨機(jī)延遲微分方程的穩(wěn)定性研究。

然而并非所有系統(tǒng)都是穩(wěn)定的,因此設(shè)計(jì)一個(gè)合適的反饋控制使不穩(wěn)定的系統(tǒng)變得穩(wěn)定很有意義。 相應(yīng)地,文獻(xiàn)[8 -11]研究了系統(tǒng)穩(wěn)定化問(wèn)題。其中文獻(xiàn)[8]研究了常時(shí)滯反饋控制的高階非線(xiàn)性混合隨機(jī)時(shí)滯微分方程的指數(shù)穩(wěn)定性,文獻(xiàn)[9]是在文獻(xiàn)[10]的基礎(chǔ)上進(jìn)一步研究了變時(shí)滯反饋控制的HNSDDEs 的Lp漸進(jìn)穩(wěn)定性和H∞穩(wěn)定性。

本文采用Lyapunov 函數(shù)方法,進(jìn)一步研究了變時(shí)滯反饋控制下的HNSDDEs 的指數(shù)穩(wěn)定性。 文獻(xiàn)[8]研究了常時(shí)滯反饋控制下的混合隨機(jī)微分延遲方程的指數(shù)穩(wěn)定性,其所涉及的時(shí)滯均為常量,本文進(jìn)一步將常時(shí)滯推廣到了函數(shù)時(shí)滯,并且將受控方程推廣到了帶有中立項(xiàng)的混合隨機(jī)延遲微分方程,其難點(diǎn)在于找到時(shí)滯δ(t)的上界和利用引理2 處理中立項(xiàng)。 文獻(xiàn)[9]研究了變時(shí)滯反饋控制的具有時(shí)變延遲的高度非線(xiàn)性HNSDDEs 的Lp漸近穩(wěn)定性和H∞穩(wěn)定性,但缺少指數(shù)穩(wěn)定性,本文則是通過(guò)進(jìn)一步找到更合適的反饋函數(shù)確定了方程的收斂速度,即指數(shù)穩(wěn)定性。

1 基本假設(shè)與模型描述

設(shè)(Ω,F,{Ft}t≥0,P)是一個(gè)帶有σ流(滿(mǎn)足通常條件)的完備概率空間,{B(t)}t≥0是定義在其上的m維布朗運(yùn)動(dòng),{r(t)}t≥0是右連馬氏鏈且獨(dú)立于{B(t)}t≥0,S= {1,2,…,N}是其狀態(tài)空間,Γ=(γij)N×N是其生成算子。

考慮變時(shí)滯反饋控制HNSDDE

其中^x(t) =x(t) -N(x(t-τ(t)),t,r(t)),且初值滿(mǎn)足

2 主要結(jié)論與證明

定義片段過(guò)程

需要注意的是,關(guān)于控制函數(shù)u的選取,考慮如下特殊情況

其中a＞0,b＞c＞0。 由于|x|2,|y|2的系數(shù)均為正數(shù),因此只能得到原方程的矩有界性,而得不到穩(wěn)定性。 此時(shí)可選取u(x,t,i) =Ax,其中矩陣A為實(shí)對(duì)稱(chēng)正定矩陣,且滿(mǎn)足λmax(A) ＜-2a,從而

故加上控制項(xiàng)之后的系統(tǒng)指數(shù)穩(wěn)定。

假設(shè)7 存在U∈C2,1(Rn×R+×S;R+),H∈C(Rn;R+),及常數(shù)0 ＜α＜1,0 ＜β＜λ,0 ＜λ1,λ2,λ3,ρ1,ρ2,使得對(duì)任意的x,y∈Rn,i∈S,t∈R+有

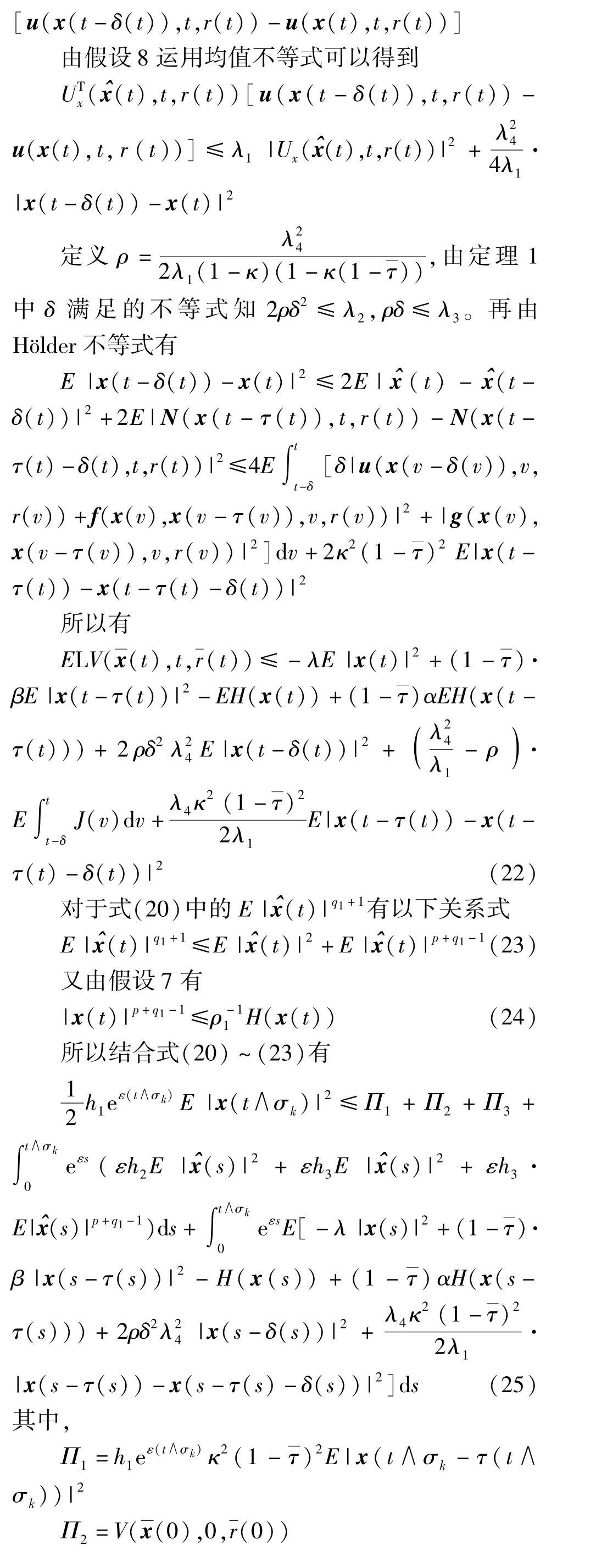
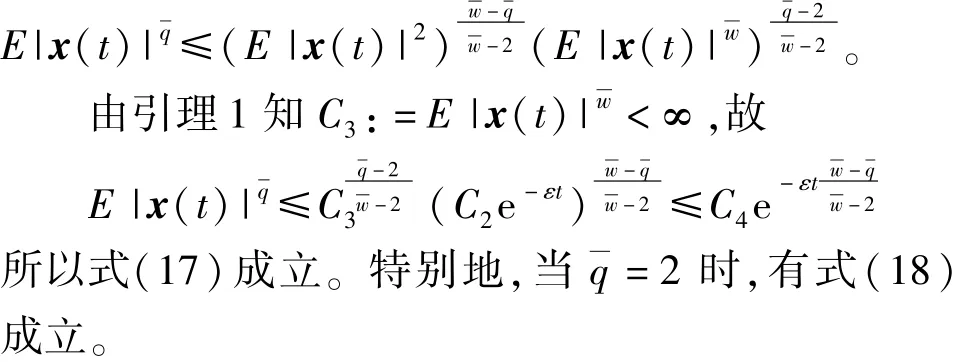
3 例子

考慮一維HNSDDE

由文獻(xiàn)[10]可知系統(tǒng)(30)不穩(wěn)定,以下將通過(guò)引入一個(gè)反饋控制函數(shù)使系統(tǒng)穩(wěn)定。

增加控制函數(shù)u(x,t,1) = -x,u(x,t,2) =-2x,增加控制函數(shù)后系統(tǒng)(3)的具體形式為

4 結(jié)論

本文采用函數(shù)方法,受文獻(xiàn)[5]的啟發(fā)在多項(xiàng)式增長(zhǎng)的條件下討論了變時(shí)滯反饋控制下的HNSDDEs 的指數(shù)穩(wěn)定性。 最后,用一個(gè)例子證明了結(jié)論的有效性。