相關干涉儀測向的定點數矩陣設計及FPGA驗證

張承暢， 楊建鵬， 羅 元， 王富強

（重慶郵電大學光電工程學院，重慶 400065）

0 引 言

相關干涉儀無線電測向算法的FPGA實現中涉及大量的二進制定點數矩陣運算，增加了FPGA 設計的設計復雜度。在FPGA中廣泛使用帶有專用浮點單元（Float-Point Unit，FPU）的DSP來處理浮點數，浮點數可以在更大的動態范圍內提供更高的分辨率，但是運算速度慢，消耗邏輯資源較多；定點數計算相對消耗邏輯設計資源較少，運算速度較快，但限制字長的情況下精度較低，并且在HDL開發方式中不容易發現因為給定字長和小數位不足造成溢出或誤差過大的問題［1］。另外FPGA 硬件驗證時，使用HDL 代碼開發的方法，在沒有完整硬件設備的條件下，無法提供復雜的波形輸入，難以發現算法中的錯誤。

針對以上問題，本文使用軟硬件聯合仿真工具System Generator 來設計和實現相關干涉儀測向的FPGA算法，管理定點數并從Simulink 提供復雜的數字信號［1-3］。

1 相關干涉儀測向原理

平面波進入天線陣時，由于到達2 個天線單元的時間有先后，該時間差使兩天線單元的反應波形產生一個射頻相位延遲或射頻相位差［4］。

圖1 所示為基本的相位延遲原理，波長λ 的平面波以入射角θ入射到天線1 上，并在天線1 上產生感應電壓U1ejωt，該平面波再經過dcos θ（d稱為基線）這段距離的傳播到達天線2 并產生感應電壓U2ejωt-τ，其相位延遲

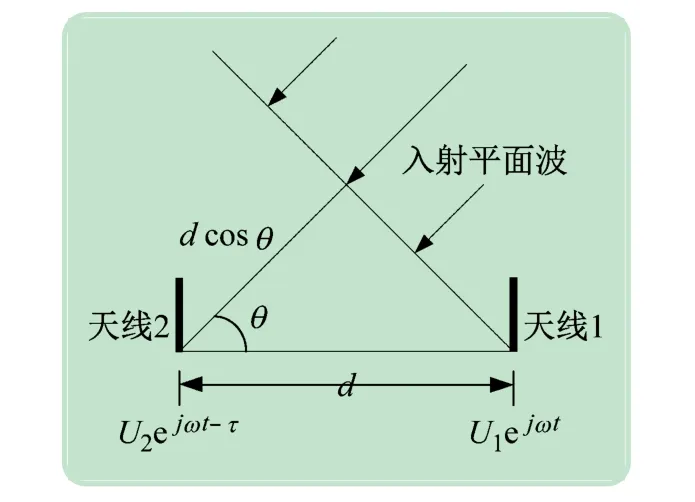
圖1 相位差產生原理圖

因此，θ是τ的函數［5-6］。

圖2 所示為五元陣基線示意圖，考慮到天線遮擋和互耦效應，天線陣列中靠近的2 個陣元之間會相互影響。因此將五邊形的5 條對角線作為低頻段測向基線，這種方法與采用相鄰線作為測向基線相比，可使天線陣規模即各天線元之間的距離進一步增大，減少了天線之間的互耦影響，并使測向精度得到改善。5 條基線代表的天線對分別為1-3，2-4，3-5，4-1，5-2。在測試高頻信號時，為了防止相位模糊，基線代表的天線對切換為1-2，2-3，3-4，4-5，5-1，即采取短基線。這些組合的相位差信息稱為標準樣本［7-8］。

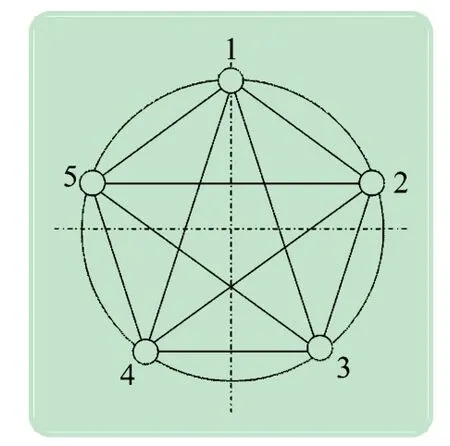
圖2 五元圓陣基線示意圖

由式（1）可推導出各基線的陣元之間的相位差［9］

式中：M為測向天線圓陣的陣元個數；R為圓陣的半徑；λ為入射電磁波信號的波長；m、n分別為陣元。將5 組相位差組合為一個標準樣本向量

所有角度的標準樣本向量的組合即為標準樣本庫。待測來波信號從某一方向入射到天線陣列時，選取與建立樣本庫時同樣的組合方式，以各基線的兩天線為1 次雙通道輸入，測得兩通道之間的相位差。5個基線的相位差組合為1 個實測樣本向量

得到待測真實入射信號的實測樣本向量后，在標準樣本庫的各角度對應的標準相位差樣本中進行搜索，可以找到一組同待測向量相似性最高的樣本向量，該樣本向量對應的入射角度值即為實測信號的到達方向估計值［10-11］。最相似樣本的搜索方式將直接影響測向的準確性，搜索方式一般為二者的相關匹配函數計算，用來評價待測相位差向量與標準相位差向量的相似性函數為代價函數，即

2 相位差矩陣運算建模

2.1 系統設計

圖3 所示為測向計算過程及輸入輸出的System Generator建模，其中輸入和參數通過gateway in 模塊二進制量化以及轉化為在FPGA 中的數據，經過運算后通過gateway out模塊回傳并轉化為Simulink軟件數據。

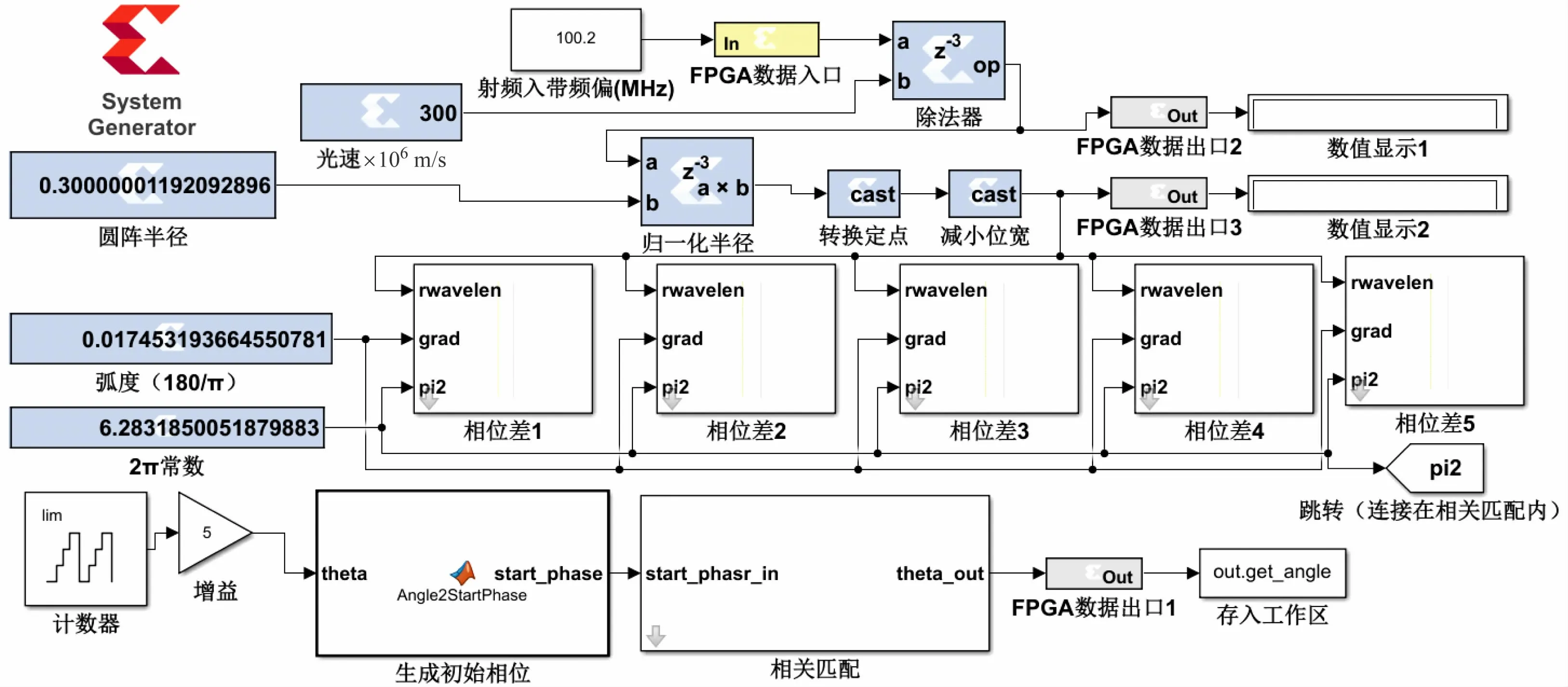
圖3 System Generator下相關干涉儀設計模型

將Simulink子系統添加封裝（Mask），以便使子系統擁有參數對話框、模塊說明、參數提示和幫助文本。在System Generator測向相位差矩陣運算系統建模中，起著自頂向下管理著子系統內模塊特定參數或多個模塊共同參數的作用，例如定點數字長、定點數二進制小數位數、寄存周期以及CORDIC算法的迭代次數等。

2.2 CORDIC模塊設計

坐標旋轉數字計算機（Coordinate Rotation Digital Computer，CORDIC）算法在數字信號處理的硬件系統中有著廣泛的應用，通過迭代的坐標系旋轉來逼近最終結果。通訊領域以及矩陣處理的三角函數、反三角函數、對數、平方根等計算都離不開CORDIC算法［12］。

本文設計的CORDIC算法模型以求取定點數的余弦函數，在旋轉模式下使用并行結構的迭代方法實現，并增加流水線以改善性能。由于CORDIC 算法僅對-π／2 ～π／2 范圍內的輸入角度z收斂，所以必須對范圍外的輸入角度進行旋轉與映射，如圖4 所示為CORDIC模塊模型設計。首先是周期變換，在輸入前經過加減運算后的輸入角度范圍為-3π ～3π，經過周期變換等價于-π ～π；其次是角度旋轉，對于第2 象限的輸入角度，通過減去π／2 映射到第1 象限；對于第3 象限的輸入角度，通過加上π／2 映射到第4 象限，這就滿足了CORDIC算法的收斂要求。角度旋轉同時又造成了計算三角函數結果時，與原本三角函數值相比產生了π／2 的相位差，所以應當應用以下三角恒等式進行校正［13-15］：

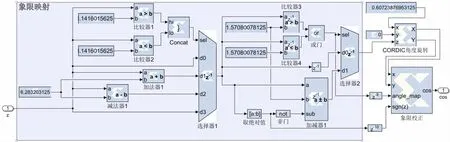
圖4 CORDIC模塊的模型設計

若輸入角度z＞π／2，則有：

若輸入角度z＜π／2，則有：

3 相關干涉儀的定點數測向仿真結果

System Generator建模中，相位差系數的取值范圍為-2π ～2π，設定其定點數字長m＝18，二進制小數位數n＝14，符號位占用首位，定點數格式表示為SFIX_18_14。以0，5，10，…，360 角度向量為標準角，建立相位差標準庫。在System Generator 中進行建立標準庫的定點數仿真，得到大小為5 ×73 的定點數矩陣，其中每一行向量，都代表對應一條基線的相位差系數理論值，每一列向量，都代表對應標準角下5 條基線的相位差系數理論值。

將System Generator建模仿真取得的樣本庫行向量，與理想化的樣本庫行向量相減，求取誤差，如圖5所示。由圖可知，誤差以0 為中心，準確度較好，定點數計算的誤差不超過0.01，與相位差系數的取值范圍-2π ～2π相比可忽略不計。

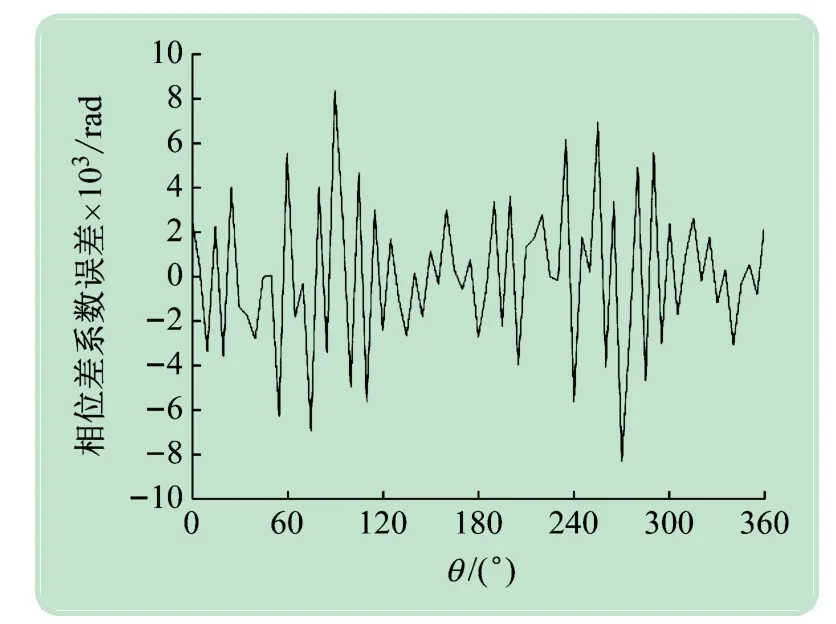
圖5 樣本庫定點數仿真誤差

在Simulink平臺上，設定基帶信號頻率100 Hz，載波頻率100 MHz，構造調制波形，并在仿真中加入了頻率偏移。根據調制波形到達5 根天線的距離不同，及天線陣列的形狀，計算信號到達5 根天線的延時。以此時延構造5 信道初相不同的數字信號作為測向系統的輸入，計算5 條基線兩兩之間相位差，得到5 ×1 向量。將此向量與樣本庫5 ×73 矩陣的每一列向量對比，計算相關匹配函數，得到1 ×73 向量，結果如圖6所示。相關匹配函數越大，代表該實際相位差與該標準角的理論相位差系數越接近。

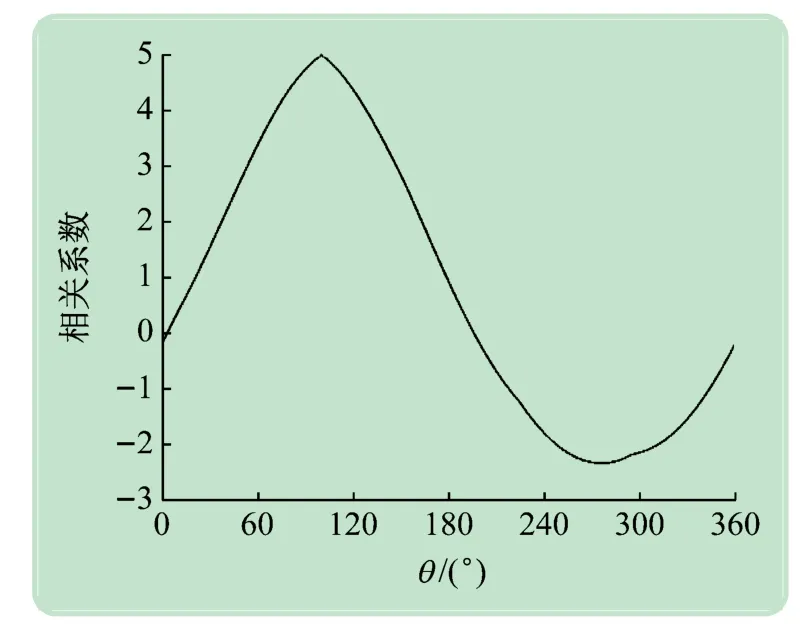
圖6 相關匹配函數定點數仿真結果

為降低硬件資源消耗，采用的標準庫以5°為間隔建表，搜索得到的角度只是粗略估計。為了提高精度，進一步提取相關匹配函數最大值的相鄰2 個值，作插值運算，得到角度計算值。輸入按時間變化的角度值產生的相位輸入，System Generator輸出格式為時間序列，時間單位為5 ns，即指定Vivado 的時鐘頻率和采樣頻率200 MHz。

將測向功能的定點數仿真的結果與理論角度值的誤差，取絕對值，仿真結果如圖7 所示，平均誤差為1.167°。

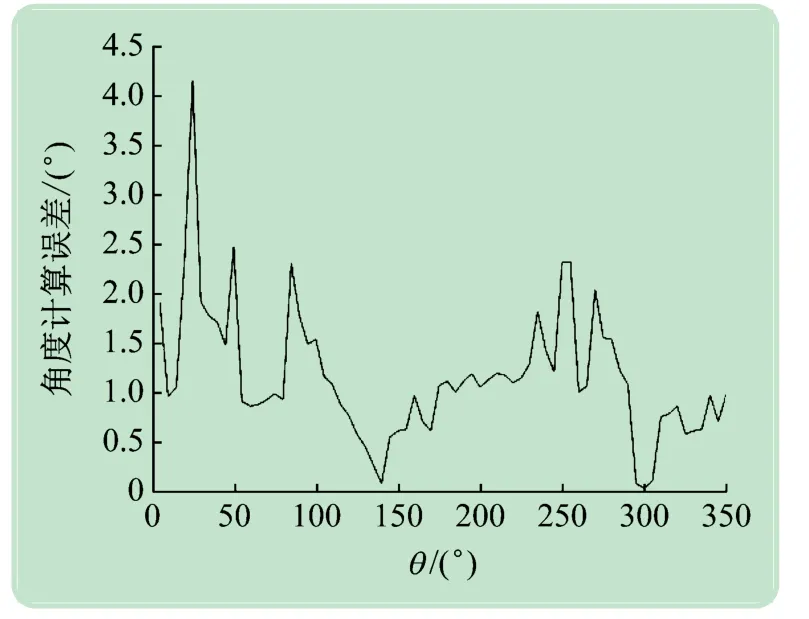
圖7 角度仿真誤差

仿真成功后，將System Generator設計生成Vivado工程，FPGA 仿真結果如圖8 所示。進一步生成比特流文件，通過JTAG連接FPGA與上位機，進行軟硬件協同運行，在Simulink 中實時產生數字信號代替實際信號，通過AXI總線提供給FPGA硬件，FPGA計算結果再通過AXI總線采樣將數據傳輸至上位機。FPGA測試的角度誤差如圖9 所示，平均誤差為2.609°。

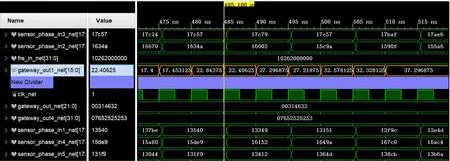
圖8 Vivado仿真界面

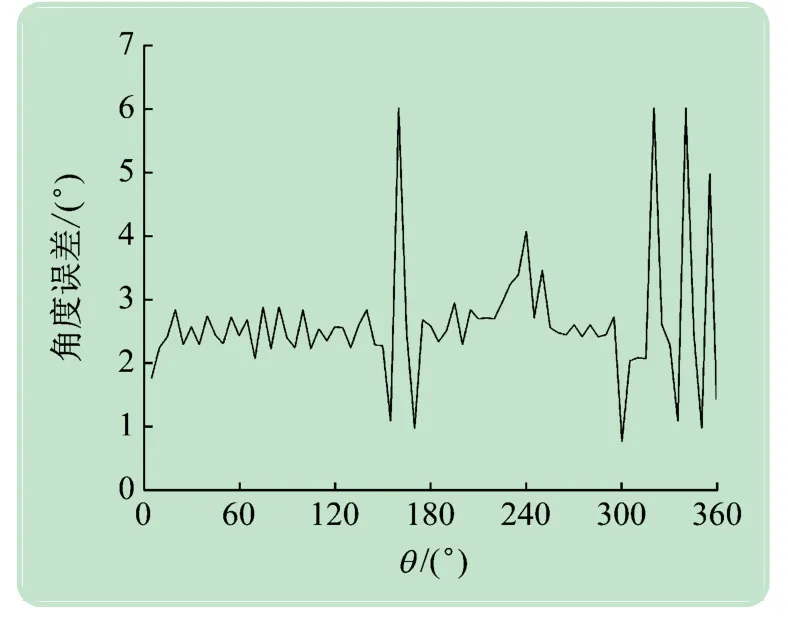
圖9 FPGA測試角度誤差

4 結 語

本文設計并完成了相關干涉儀測向系統FPGA算法的建模，使用Simulink可視化FPGA進行了仿真，進一步生成Vivado 工程并完成FPGA 的軟硬件協同仿真運行實驗。結果表明：定點數仿真的平均誤差為1.167°；FPGA測試的平均誤差為2.609°，即定點數矩陣的FPGA設計方法，其仿真結果與實測數據接近。該流程為數字信號系統提供可視化的數據流和定點數管理，且可在測向項目場地測試前提供基于Simulink的復雜輸入信號用于提前測試，對于FPGA 工程的流程優化的有一定的技術參考價值。