“教學做合一”,糾正數學認知偏差的應然選擇
江蘇宜興市學府路實驗小學(214421) 王琴芳
陶行知先生認為“教學做”是一體的,其中“做”是核心,主張教師在“做”中教,學生在“做”中學。美國教育家約翰·杜威提出從“做”中學的思想,強調身體在認知中的價值,他認為,認知的過程是通過大腦、身體、環境相互連接在一起的。具身認知的理論強調學生應全身心參與數學活動,多感官體驗,身心融合,促進身體與思維的相互關聯,發揮身體在認知發展、增進兒童智慧等方面的積極作用。由于小學生的年齡特點和認知特點,他們受生活實際及知識基礎的影響,對數學知識的認知往往會有偏差。而教師就是要及時捕捉他們的認知偏差,并通過對真實情境的模擬與重現,充分調動學生的多感官參與、多維度體驗、多元化感悟,借助體驗式實踐來辨析,從而去偽存真,正確建構數學概念。
一、互動式討論,糾文本理解之偏差
小學生的思維以具體形象思維為主,對數學概念的學習往往停留在具體的情境中,而對于數學問題的文字的敘述會自行做不必要的補充,從而產生認知偏差。
【教學案例1】蘇教版三年級數學上冊“認識分數”
問題:下面選項中,( )是正確的。
A.一個西瓜切成3塊,吃了2塊,吃了這個西瓜的三分之二。
B.有兩個杯子,各裝了半杯水,把兩個半杯倒在一起就是一杯水。
C.把一張正方形紙連續折兩次,每份是這張紙的四分之一。
D.五分之三里有5個三分之一。
生1:我覺得這道題出錯了,應該是選錯誤的,因為只有一個錯誤的選項。
(絕大多數學生都有同樣質疑。)
師:你們覺得哪個選項是錯誤的?
生2:只有D選項是錯誤的,其余都是對的。
師:認為A選項正確的同學說說理由。
生3:將西瓜分成了3塊,2塊就是三分之二。
生4:我反對,如果我分的不是相等的3 塊,就不對了。
生5:老師,B選項的這兩個杯子一樣大嗎?
師:題目中有沒有說是同樣大的杯子呢?
生6:這兩個杯子有可能一個大,一個小。
生7:C 也不正確呀,連續折兩次,不一定每份一樣大呀!
(生7 拿出一張正方形紙示范起來,先沿對角線對折一次,再沿著側邊折一次,果然沒有將紙平均分成4份。)
師:你們覺得呢?
生8:這樣不是對折。
以上案例中,學生受生活經驗的影響,默認分物品時都要平均分,要想糾正這種認知偏差,在新授課時就要通過反例強化分數的意義;在學生產生爭論時,提供實踐的演示與圖例的說明,讓錯方深刻認識到錯誤的原因,從而達成糾錯的目的。
二、實境式辨析,糾負面遷移之偏差
數學是一門邏輯性極強的學科,而知識的遷移則是學好數學的重要路徑。但在具體教學中,學生常常會在知識點之間產生負遷移,從而產生錯誤。
“間隔排列”的教學通常是從情境圖入手,讓學生觀察圖上物品的擺放特點,從而找出規律,在練習中有相應的圖示作為習題的范例,因此很少有學生會出錯。但當問題只以文字形式呈現時,學生的認知偏差就產生了。比如問題“24 名男生站1 排,每2名男生之間站1名女生,一共要站幾名女生?”,有學生答24÷2=12(人)。究其原因,他是受除法含義的影響,看到“每2 名男生”就以為是將每2 人分成1 份,選擇用除法計算,這是由已有知識經驗產生的負遷移。怎樣讓學生理解“每2 名男生之間站1 名女生”?可以讓學生進行實境模擬,讓男生站1排,引導學生思考“在什么位置上站女生”。學生通過親身體驗感受到“每2 名男生之間”就是“第一名男生和第二名男生之間站1 名女生,第二名男生與第三名男生之間站1 名女生……”,而非“隔2 名男生站1 名女生”,也就不存在“每2 人分1 份”這一說法。
上述案例中,學生由于對除法含義理解不透徹產生負遷移,誤認為只要看到“每幾個”就是平均分,不自覺地將“間隔排列”的規律與除法勾連起來,選擇用除法來解決問題。在糾錯過程中,首先,要讓學生思維外顯,即通過實境模擬或者畫圖表示出題目的含義,再通過引導學生觀察思考“間隔排列”的規律與除法含義有無關聯,從而作出正確的判斷;其次,針對不同的圖例表達,要引導學生對照條件,突破理解題意之難點;最后,還要讓學生進行必要的變式練習。在教學中,只有讓學生在實境中充分感知,加強對比與辨析,才能讓學生真正認識數學的本質,從而糾正負遷移產生的認知偏差。
三、實踐式探究,糾順向推理之偏差
數學學習離不開推理,而學生對論證方法的運用有限,得到的推論并不完全正確。作為教師既要鼓勵學生大膽推理,又要提醒他們小心求證。
【教學案例2】蘇教版小學數學四年級下冊“三角形的內角和”
(學生通過計算熟悉的直角三角尺的三個內角的度數之和引發猜想,再通過舉例驗證,得出“三角形的內角和是180°”的結論。)
師:用兩塊完全一樣的三角尺拼成不同圖形,拼成圖形的內角和分別是多少?
生1:如圖1 所示,我拼成了平行四邊形,內角和是360°。

圖1
生2:如圖2 所示,我拼成了長方形,內角和也是360°。

圖2
生3:如圖3 所示,我拼成了正方形,內角和也是360°。

圖3
生4:我覺得不管拼成什么圖形,內角和總是360°,因為三角形的內角和是180°,2個三角形拼成的圖形,內角和就是180°×2=360°。
師:大家拼的圖形內角和都是360°嗎?
生5:我拼成的是三角形,內角和不是360°。
師:大家也來試著拼三角形,看看內角和到底是多少度?
(學生拼成的三角形如圖4、圖5、圖6所示。)

圖4

圖5
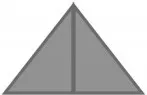
圖6
生6:圖4的內角和為60°+60°+30°+30°=180°。
生7:圖5的內角和為30°+30°+60°+60°=180°。
生8:圖6的內角和為45°+45°+45°+45°=180°。
(學生對拼成三角形的內角和與前面拼成長方形、正方形的內角和不同而產生了認知沖突。)
師:仔細觀察比較,拼成三角形與拼成四邊形到底有什么區別?
生9:拼成三角形時2 塊三角板的2 個直角都被拼掉了,只有4 個銳角成了新的三角形的角。因此,內角和是360°-90°-90°=180°。而拼成平行四邊形、長方形或正方形時,由于內角都未被拼掉,所以內角和就是180°+180°=360°。
在上述案例中,學生的認知偏差源于順向推理,當有例子是正確的時,學生就大膽猜想所有例子都正確。教師借助特例組織學生共同研究,讓學生用實驗的方式得到結論,再用動手實踐的方式來探究兩類圖形的區別。這樣,不僅培養了他們的合作交流、數學推理能力,還發展了他們的空間觀念,激發了他們學習數學的興趣,更為他們將來探究數學本質明確了路徑。
四、具身式想象,糾視覺空間之偏差
數學概念具有抽象性,而小學生思維又以具體形象思維為主,因此,在具體學習過程中,學生往往會受視覺的影響,產生認知上的偏差。
【教學案例3】蘇教版小學數學三年級上冊練習
師(出示圖7):在圖中里添一個正方形,使它成為一個軸對稱圖形,至少畫3種。

圖7
(學生通過討論交流,很快出現了3 種畫法,如圖8、圖9、圖10所示。)

圖8

圖9

圖10
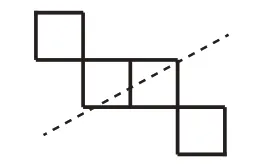
圖11
(也有學生提出,把正方形添在右下側,如圖11所示,還特意畫出了對稱軸。)
師:大家想想,這樣的圖形是不是軸對稱圖形呢?
生1:不是,因為它對折后不能完全重合。
生2:可是它兩邊的圖形是完全相同的呀!
師:剛剛有同學說兩邊的圖形明明就是完全相同的,怎么就不是軸對稱圖形呢?
生3:雖然兩邊圖形完全相同,但它們對折后并不能完全重合,因此不是軸對稱圖形。
生4:軸對稱圖形不是看兩邊是否完全相同,而是應該看對折后能否完全重合。
上述案例,如果教師僅僅強調它是錯的,而不讓學生說出自己的理由,那么就無法觸及學生的錯誤認知,也無法幫助他們區分“完全相同”與“對折后完全重合”之間的區別。只有讓學生說出自己真實的想法,通過討論、交流、具身想象,學生才能辨析其正誤,糾正存在于腦中的認知偏差,從而對數學概念有準確的把握。
五、化歸式抽象,糾概念混淆之偏差
數學概念之間相互關聯,既有區別又有聯系。在教學中,學生經歷知識的發生、發展和形成,但缺少必要的化歸,導致在知識運用過程中出現張冠李戴、概念混淆的現象。
【教學案例4】蘇教版五年級數學“平行四邊形面積計算”
師(出示圖12):求該平行四邊形的面積。
(不少學生選擇了用15×12=180(平方分米)來計算。學生是套了“平行四邊形面積=底×高”這一公式。顯然,此類錯誤是因為學生對于平行四邊形中的底與高的關系不清晰。)
師:大家實踐操作,用不同方法將平行四邊形轉化成長方形。
(學生找到的方法如圖14所示。)

圖14
師:觀察不同轉化方法,有什么共同點?
生1:通過觀察與比較,我發現平行四邊形沿著與底對應的高剪下后都可以拼成長方形。
師:剛才你們不約而同想到了沿著與水平方向的底對應的高來剪,然后拼成長方形,那還可以怎樣剪拼呢?
生2:還可以沿著另一組底對應的高來剪,然后拼成長方形。
師(引導觀察思考):這些不同的轉化方法又有什么共同點?與前一類的轉化方法有什么相同與不同?
上述案例中,學生之所以會產生這樣的認知偏差,是因為只知道平行四邊形面積是底與高的乘積,沒有理解為什么,對平行四邊形中底與高的概念沒有清晰的認知。在教學過程中,教師應充分展示轉化的過程,引導學生借助觀察、討論、比較,進行化歸式抽象,得出底與高是對應關系,是相互垂直的一組線段,從而糾正學生的錯誤認知。學生經歷了兩種不同的轉化過程,獲取了轉化的直觀感悟,通過觀察、比較,抽象出轉化的本質,理解了平行四邊形面積計算方法的本質。在教學中,概念、公式等數學知識的獲得都應該讓學生有充分感悟的時間和空間,經歷數學知識形成的過程,在直觀表象的支撐下抽象出數學的本質,即尋找共同屬性,排除非本質屬性的干擾。
小學數學概念認知偏差的糾正依賴于學生具身參與,是一種多感官參與、多維度體驗、多方位關聯的活動,不僅能發展學生動手操作、空間想象、合情推理、抽象概括等能力,更是溝通學生身體與思維的橋梁。學生身心融合,主動參與實踐,抽象出數學本質,方能讓數學概念的認知偏差得以糾正,建立網狀的認知結構,實現數學思維的進階。

