邊破壞對多智能體系統能控性的影響

肖朋朋，紀志堅

（1.青島大學 自動化學院，山東青島 266071；2.山東省工業控制重點實驗室，山東青島 266071）

隨著社會的發展和科技的進步，國內外眾多學者對多智能體系統的研究逐步深入，網絡拓撲為研究多智能體系統提供了一種分析工具。近年來，多智能體系統不僅在控制領域，在無人機編隊等領域[1-8]也進行了深入研究。

能控性概念是上個世紀60 年代由卡爾曼首次提出，2004 年能控性的概念被引入到多智能體的研究當中。近些年，多智能體系統研究取得了顯著的成就，如自適應控制[9-11]、博弈控制[12-14]、切換系統[15]等都已應用于多智能體系統中。一類邊集失效對復雜網絡能控性的影響已經有過討論[16]，但不同類型的邊失效對多智能體系統能控性的影響，以及對拉普拉斯矩陣秩的影響，目前還沒有給出確切的結論。因此，為了解決此問題，將系統中的邊進行分類，并從理論層面給出不同類型的邊失效對系統能控性影響的確切結論。文中提出了一種邊的分類方式，將多智能體系統中的邊分為三種類型，邊組合分為四種組合類型，并提供了一種辨識邊類型的算法，給出了不同類型的邊失效后系統能控性的變化規律。同時，為了保證邊失效后的系統是能控的，給出了領導者的選擇方法，最后通過實例驗證了結論。

1 預備知識

1.1 圖論知識

對于含有N個節點的多智能體系統G(A)=(V,E,A)，其中V={v1,v2,…,vN} 表示系統的節點集，E={e1,e2,…,eN}表示系統的邊集，A=[aij]∈RN×N表示加權鄰接矩陣，aij表示節點j對節點i的影響程度，若無特殊說明，aij=1。文中不考慮存在自環的情況，即(vi,vi)?E。Ni={j∈V∣(j,i)∈E}表示節點i的鄰居集合。在有向圖G中，對于不同的節點i、j，都有一條從i開始到j結束的定向路徑，則稱圖G為強連通圖。di=||Ni表示節點i的度，有向圖G的度矩陣為D(G)=diag(d1,d2,…,dN)。拉普拉斯矩陣(Laplacian matrix)是相較于度矩陣的另一種表達圖中頂點關系的矩陣，拉普拉斯矩陣可以用L(G)=D(G)-A(G)表示。

1.2 數學符號

R表示實數集，Rn表示n維實向量空間。XY表示屬于X但不屬于Y的集合，I為單位矩陣，O表示文中合適維度的零矩陣，?表示空集。

1.3 系統模型

其中，L∈RN×N為拉普拉斯矩陣，B∈RN×P為外部控制輸入矩陣。

對于線性時不變系統（1），若存在一個分段連續的輸入u(t)能夠在有限時間[t0,tf]內使得系統從任意初始狀態轉移到任意終止狀態，則稱此系統的狀態是完全能控的。可以通過能控性判據來判斷系統是否是能控的，即系統完全能控的充分必要條件是矩陣C=[B,LB,…LN-1B] 滿秩，即rankC=N。此時，我們稱該系統是完全能控的。

定義1對于有向圖G的一個子圖G′，如果G′為單向強連通環圖，且對于任意j∈V/V′，i∈V′，都有(i,j)?E，強連通子圖G′整體只有單個輸入，這種結構稱為InSCC。在文中將InSCC 結構外且沒有入度的節點作為初始節點，即節點1 為初始節點，如圖1所示。

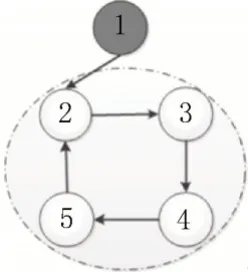
圖1 InSCC結構

2 多智能體系統中邊的分類辨識

在含有InSCC 結構的多智能體系統中，邊失效后，系統的能控性怎樣變化以及如何再次選擇領導者保證系統能控，都是十分有意義的問題。

2.1 多智能體系統中邊的分類

含有InSCC 結構的多智能體系統通常由節點和有向邊組成，其中節點存在三種類型，邊也存在三種類型。

2.1.1 邊的分類

類型1：如圖2（a）所示，對于多智能體系統中的一條邊，如邊(v1→v2)，如果和初始節點相連，則這條邊為關鍵邊，記作xK。

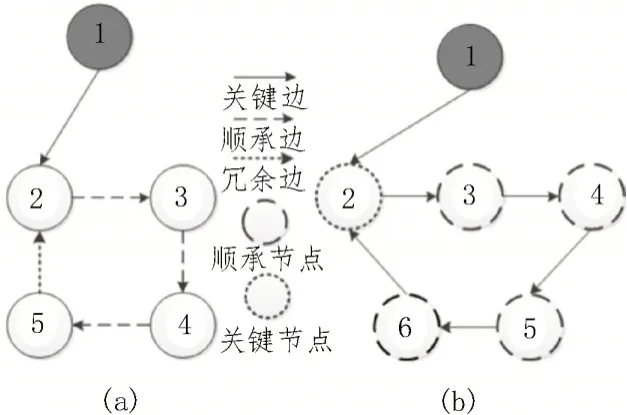
圖2 節點和邊在網絡中的關系

類型2：如圖2（a）所示，對于多智能體系統中的一條邊，如邊(v2→v3)或(v3→v4)，如果一條邊由關鍵節點指向順承節點或者由順承節點指向順承節點，則這條邊為順承邊，記作xF。

類型3：如圖2(a)所示，對于系統中的一條邊，如邊(v6→v2)，如果一條邊由順承節點指向關鍵節點，則這條邊為冗余邊，記作xR。

2.1.2 節點分類

類型1：如圖2（b）所示，對于多智能體系統中的一個節點，獨立于InSCC 結構外且沒有入度的節點作為初始節點，如節點1。

類型2：如圖2（b）所示，對于多智能體系統中的一個節點，和初始節點相連的邊指向的節點為關鍵節點，如節點2。

類型3：如圖2（b）所示，對于多智能體系統中的一個節點，順承邊指向的節點為順承節點，如節點3、4、5 和6。

2.2 多智能體系統中邊組合失效類型

根據節點和邊的類型，對不同邊的組合進行分類，每個組合有且僅有兩條邊。

類型1：關鍵邊和順承邊遭到破壞而失效，則失效組合為關鍵邊-順承邊組合，記xK-F。

類型2：關鍵邊和冗余邊遭到破壞而失效，則失效組合為關鍵邊-冗余邊組合，記xK-R。

類型3：順承邊和順承邊遭到破壞而失效，則失效組合為順承邊-順承邊組合，記xF-F。

類型4：順承邊和冗余邊遭到破壞而失效，則失效組合為順承邊-冗余邊組合，記xF-R。

2.3 邊組合的辨識算法

為了更好地探究邊失效對多智能體系統能控性的影響，需要找出多智能體系統中邊的類型，下面給出多智能體系統中邊的辨識算法，具體步驟如下：

Step1：遍歷多智能體系統中的所有節點，如果存在一條邊(vi→vj)，其中節點vi為初始節點，那么由節點vi指出的邊為關鍵邊。

Step2：遍歷多智能體系統中的所有節點，如果存在一條邊(vi→vj)，其中節點vi為關鍵節點或者為順承節點，節點vj為順承節點，那么由節點vi指向節點vj的邊為順承邊。

Step3：遍歷多智能體系統中的所有節點，如果存在一條邊(vi→vj)，其中節點vi為順承節點，節點vj為關鍵節點，那么由節點vi指向節點vj的邊為冗余邊。

Step4：搜尋第一條與初始節點相連接的邊為關鍵邊，如果第二條邊是從關鍵節點或順承節點vj出發，到順承節點vj+1結束，邊(vj→vj+1)為順承邊，則找出關鍵邊-順承邊組合xK-F，否則進行下一步。

Step5：搜尋第一條與初始節點相連接的邊為關鍵邊，如果第二條邊是從順承節點vj出發，到關鍵節點vj+1結束，邊(vj→vj+1)為冗余邊，找出關鍵邊-冗余邊組合xK-R。

Step6：搜尋第一條邊從關鍵節點或順承節點vi出發，到順承節點vi+1結束，邊(vi→vi+1)為順承邊，如果第二條邊是從關鍵節點或順承節點vj出發，到順承節點vj+1結束，邊(vj→vj+1) 為順承邊，那么邊(vi→vi+1)與邊(vj→vj+1)的組合為順承邊-順承邊組合xF-F，否則進行下一步。

Step7：搜尋第一條邊從關鍵節點或順承節點vi出發，到順承節點vi+1結束，邊(vi→vi+1)為順承邊，如果第二條邊是從順承節點vj出發，到關鍵節點vj+1結束，邊(vj→vj+1)為冗余邊，那么邊(vi→vi+1)與邊(vj→vj+1)的組合為順承邊-冗余邊組合xF-R。

3 邊失效對多智能體系統能控性影響

定理1 對于含有N個節點的多智能體系統，其中含有n個不同的InSCC 結構。

1）當失效n條關鍵邊時，多智能體系統的能控子空間維數降低。rank(LK)=N-n-1，LK為丟失關鍵邊后的拉普拉斯矩陣。保證丟失n條關鍵邊后的多智能體系統是能控的，需要選擇初始節點和n個關鍵節點為領導者。

2）當失效n條順承邊時，多智能體系統的能控子空間維數降低。其中每個InSCC 結構失去一條順承邊，rank(LF)=N-n-1，LF為丟失順承邊后的拉普拉斯矩陣。保證丟失n條順承邊后的多智能體系統是能控的，需要對初始節點和n個失效順承邊指向的順承節點施加外部控制輸入。

3）當失效n條冗余邊時，多智能體系統的能控性保持不變，對應的拉普拉斯矩陣LR的秩不變。當選擇初始節點為領導者時，多智能體系統能控性保持不變。

證明：1）當n條關鍵邊失效時，其所對應的拉普拉斯矩陣為：

因為系統含有n個不同的InSCC，所以矩陣LKi的維數不相同。接下來計算在矩陣LK的特征值中零特征值的重數：

其中，LK0=0，每個|λI-LKi|中存在一個特征值λ=0，所以在LK的特征值中，λ=0 的重數為n+1，即rank(LK)=N-n-1。

當選擇初始節點為領導者時，關鍵邊失效后的系統存在N-1 個輸入不可達節點，系統的能控子空間維數降低。根據InSCC 結構的特性，當多智能體系統中所有的節點輸入可達時，系統能控。保證丟失n條關鍵邊后的多智能體系統是能控的，選擇輸入矩陣B=[bK0,bK1,…,bKn]，其 中bK0=[1,0,…,0]T，bKi=[0,…,?,…,?]T，bKi∈RN×1，i∈{1,2,…,n} 。當在關鍵節點施加外部控制時，?=1，否則?=0，此時丟失關鍵邊后的系統所有節點是輸入可達的，系統能控。

2）當n條順承邊失效時，其中每個InSCC 結構失去一條順承邊。根據拉普拉斯矩陣行和為零的性質，拉普拉斯矩陣LF中出現n+1 個全零行，丟失n條順承邊后的拉普拉斯矩陣LF的秩減少n，因此有rank(LF)=N-n-1。保證丟失n條順承邊后的多智能體系統是能控的，則需要選擇輸入矩陣B=[bF0,bF1,…,bFn]，其中bF0=[1,0,…,0]T，bFi=[0,…,*,…,*]T，bFi∈RN×1，i∈{1,2,…,n} 。當對失效順承邊指向的順承節點施加外部控制輸入時，*=1，否則*=0，此時系統能控。

3）當n條冗余邊失效時，拉普拉斯矩陣LR中仍有N-1 線性無關的行向量，LR與冗余邊失效前的拉普拉斯矩陣具有相同的秩。當選擇初始節點為領導者時，系統中不存在輸入不可達節點。因此，冗余邊丟失前后多智能體系統能控性保持不變。

定理2對于一個含有N個節點的多智能體系統，其中含有n個不同InSCC 結構，InSCC 結構中節點數k≥3 。當丟失n組順承邊—順承邊組合(xF-F)時，每個InSCC 中丟失一組xF-F，多智能體系統的能控子空間維數降低。rank(LF-F)=N-2n-1，LF-F為丟失xF-F后的拉普拉斯矩陣。保證丟失n組xF-F后系統能控，則對初始節點和失效順承邊指向的順承節點施加外部控制輸入。

證明：對于只含有n個不同InSCC 的多智能體系統，InSCC 結構中節點數k≥3。當n組邊組合xF-F失效時，其中每個InSCC 結構失去一組xF-F，根據拉普拉斯矩陣行和為零的性質，拉普拉斯矩陣LF-F中出現2n+1 個全零行。在LF-F的特征值中，特征值λ=0 的重數為2n+1，rank(LF-F)=N-2n-1。當選擇初始節點為領導者時，邊組合xF-F失效后的多智能體系統存在輸入不可達節點，多智能體系統的能控子空間維數降低。保證丟失n條邊組合xF-F后的多智能體系統是能控的，則需要選擇輸入矩陣B=[bF0,bF1,…,bF2n]，其 中bF0=[1,0,…,0]T，bFi=[0,…,*,…,*]T，bFi∈RN×1，i∈{1,2,…,2n}。當對失效順承邊指向的順承節點施加外部控制輸入時，*=1，否則*=0，此時系統能控。

4 實例驗證

圖3（a）所示為只含有一個InSCC 的多智能體系統，系統的拉普拉斯矩陣為：

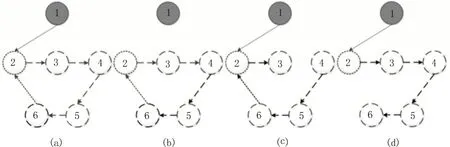
圖3 只含有一個InSCC的多智能體系統中不同類型邊失效

rank(L)=5。

1）當丟失一條關鍵邊后，如圖3（b）所示，系統的拉普拉斯矩陣為：

rank(LK)=4，關鍵邊失效后系統的拉普拉斯矩陣的秩減少1。保證丟失關鍵邊后的系統是能控的，則需要選擇初始節點和關鍵節點為領導者，即選擇輸入矩陣BK，此時，根據系統能控性判據可知系統能控。

2）當丟失一條順承邊后，如圖3（c）所示，系統的拉普拉斯矩陣為：

rank(LF)=4，順承邊失效后多智能體系統的拉普拉斯矩陣的秩減少1。保證丟失順承邊后的多智能體系統是能控的，則需要對初始節點和失效順承邊指向的那個順承節點施加外部控制輸入，即選擇輸入矩陣BF，此時，根據系統能控性判據可知系統能控。

3）當丟失1 條冗余邊后，如圖3（d）所示，拉普拉斯矩陣LR為：

其中，存在五個線性無關的行向量，因此LR與冗余邊失效前的拉普拉斯矩陣L具有相同的秩。當選擇初始節點為領導者時，系統中不存在輸入不可達節點，因此，冗余邊丟失前后多智能體系統能控性保持不變。

5 結論

文中研究了只含有InSCC 的多智能體系統在遭受攻擊或破壞后，不同類型的邊失效對網絡能控性的影響。當關鍵邊和順承邊失效時，系統拉普拉斯矩陣的秩減少，多智能體系統的能控子空間維數降低；當冗余邊失效時，系統拉普拉斯矩陣的秩不發生改變，多智能體系統的能控性保持不變；當邊組合xF-F失效時，系統拉普拉斯矩陣的秩減少，多智能體系統的能控子空間維數降低。同時，為了保證不同類型邊以及邊組合失效后的多智能體系統是能控的，給出了領導者的選擇方法。