基于機器學習的數據中心穩態熱參數預測
殷佳輝 朱兵 張一鳴 黃金森 苗益川
關鍵詞:數據中心;氣流模擬;機器學習;快速預測;熱參數
中圖分類號:TK221 文獻標識碼:A 文章編號:1006-8228(2023)11-71-06
0引言
傳統行業與云計算、人工智能、5G、物聯網技術呈深度融合的趨勢,數據及流量爆發式增長使數據中心向著大規模、高密度的方向發展[1],導致數據中心能耗逐年增加。數據中心的能耗由IT 設備、制冷系統、供配電和照明系統三部分組成。其中IT 設備占總能耗50%[2],其產生的熱量直接決定了空調負荷的大小,影響空調能耗;而空調運行參數的改變,反過來影響著IT 設備的運行環境及其運行能耗,兩者的能耗因熱環境而彼此耦合[3]。因此,以IT 設備的負載動態變化為基礎,預測數據中心的溫度情況,探索數據中心熱環境與能耗之間的平衡、對于數據中心能源優化管理具有現實意義。
基于計算流體力學(CFD)模擬的方法是預測數據中心溫度分布的主流辦法[4]。但CFD 預測過程中需求解復雜的數學物理模型,大型的數據中心機房往往需要劃分幾十萬到幾千萬的網格[5],求解過程困難,難以實現氣流的實時預測。近年來興起的機器學習預測方式使數據中心氣流組織的實時預測成為可能,對此國內外學者已有一些研究。Song Zhihang[6]開發了基于計算流體動力學(CFD)仿真的人工神經網絡(ANN)模型對高架地板入口氣流的溫度和速度預測。Tsukamoto 等[7]人開發了可基于低網格數CFD 模型計算出的機柜出口風速對高網格數CFD 模型的機柜出口風速做出預測的深度神經網絡(DNN)回歸預測模型。Athavale 等[8]評估了人工神經網絡(ANN)、高斯過程回歸(GPR)和支持向量回歸(SVR)三種機器學習方法對數據中心穩態工況下機架入口溫度分布的預測性能。石桃桃等[9]建立了多參數POD 降階溫度場預測模型,基于POD-IDW 模型預測機柜進出風平面的溫度場分布。
上述學者在數據中心氣流組織優化、模型開發和數據中心結構設計等領域取得了大量研究成果,但在模型評估與優化及穩態熱環境實時預測等領域研究不夠深入。雖然CFD 模擬可以提供實驗難以得到的特殊工況下的氣流分布數據,但目前CFD 計算中常用的湍流模型并不適合,準確性較差,難以為快速預測模型提供高保真數據。基于此,本文為提高CFD 預測數據中心氣流組織穩態熱參數的準確性,以雪城大學/IBM 綠色數據中心(GDC)實驗室(RL)[10-11]為模型。通過參數化仿真,模擬了在不同機柜負載率下的穩態溫度分布建立CFD 數據集,并基于CFD 數據集訓練將其用于Elman 神經網絡,RBF 神經網絡和SVR 支持向量回歸三種機器學習模型訓練。從而實現對不同機柜負載率下空調回風溫度的快速預測,并評估了不同機器學習模型穩態熱參數預測性能。
1 數據中心模型
1.1 實驗模型
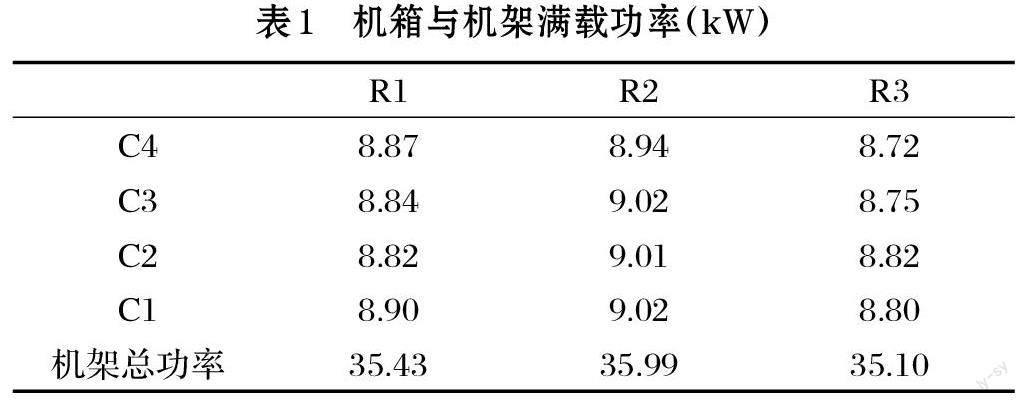
實驗室共設有R1、R2、R3 三個大功率模擬機架,每個機架長1m,寬0.61m,高2m,在滿載時可產生102kW 以上的熱量(每個機架約34kW),每個機架包含四個模擬機箱,每個機箱均設置有恒速風扇和可變功率加熱器,模擬機箱的流量特性和瞬態熱響應特性與真實IBM 刀片機箱相同。并且高架地板模型采取數據中心常用的的體積力模型;湍流模型采用standard k-e 湍流模型。每個機箱的最大功率見表1。
1.2 CFD 模型及邊界條件設置
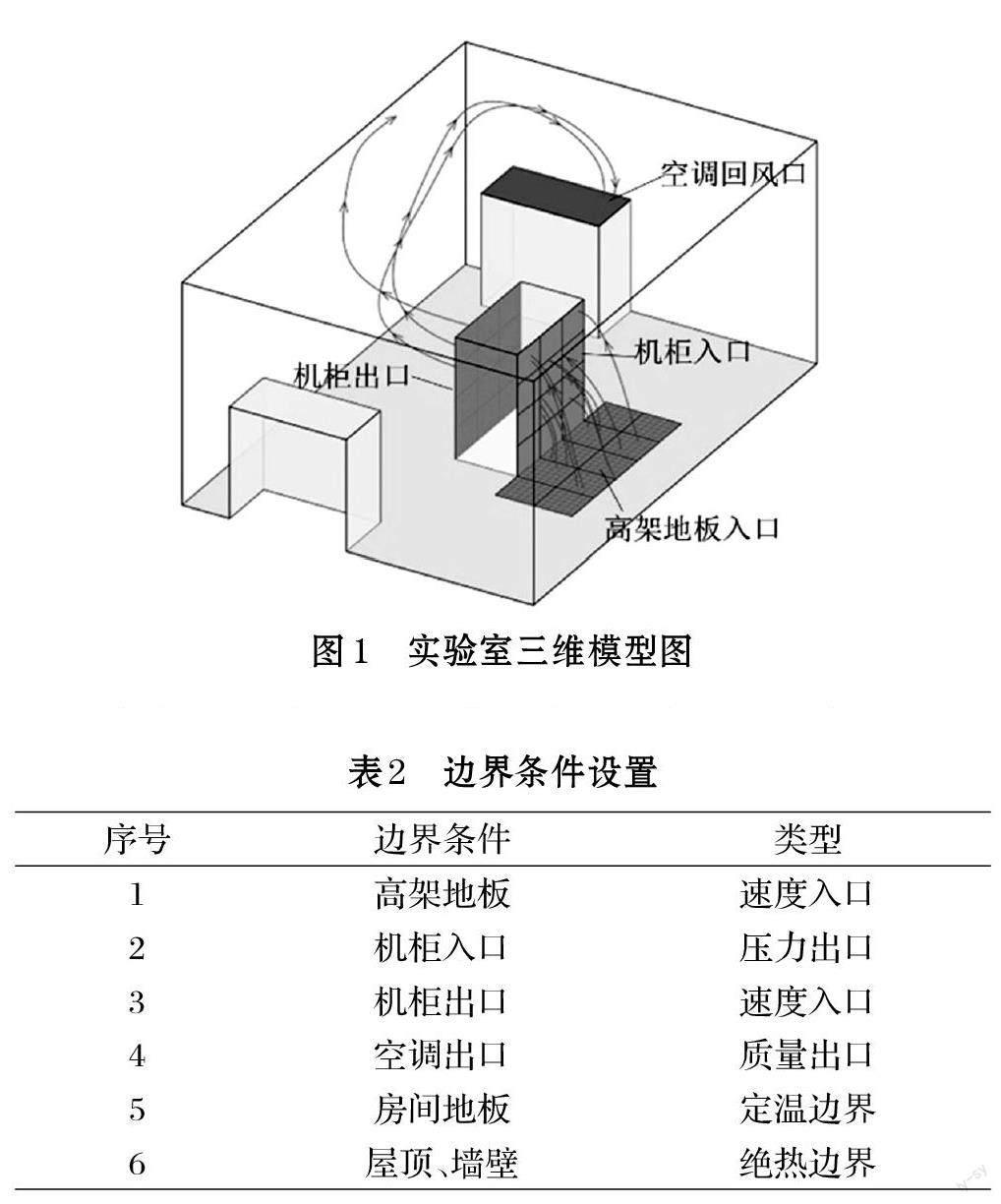
如圖1 所示,機架吸入穿過高架地板進入機房的空氣以及部分房間內的再循環空氣冷卻機架,機架的排氣進入機房與房間空氣混合,然后進入空調回風口進行降溫,冷空氣進入增壓室后穿過高架地板進入房間完成循環。
將實驗室模型的計算域包含除機柜內部和增壓室之外的整個房間,房間墻壁、天花板均為無滑移絕熱邊界、由于實驗時未開啟CRAH2 所以同樣將其設置為絕熱邊界,地板設置為溫度邊界,機柜前方十塊高架地板設置為速度入口,CRAH1 設置為質量出口,本實驗研究房間級的氣流組織,未對機柜內部氣流進行分析,將機柜建模為一個黑箱,機柜入口為壓力出口,機柜出口為速度入口,根據實驗數據對機柜進行設置,邊界條件及參數設置見表2。
穩態仿真基于三個機柜全部滿載情況下進行,數據中心實際運行過程中服務器負載變化范圍為0~100%,而負載率的變化直接影響機柜的出口溫度,因此在探究機柜出口溫度對針對12 個模擬機箱在不同的負載率下進行仿真抽樣,為了確保數據集的填充,且盡量減少仿真次數,使用拉丁超立方抽樣對12 個模擬機箱的負載率建立了容量為500 的樣本,使用黑箱模型計算出不同負載率下的機柜出風口溫度,此外,由于實驗室模擬機箱均為恒速風扇,因此機柜出口流量不發生變化。
2 機器學習模型訓練
建立CFD 數據集后,將數據集用于機器學習模型的訓練,為了建立更準確的數學模型分別采用了三種機器學習算法,包括Elman 神經網絡、RBF 神經網絡與SVR 支持向量回歸機。將12 個模擬機箱的出風溫度作為輸入參數,空調回風溫度作為輸出參數,進行了參數化仿真,完成500 組數據的仿真時間約為2500 分鐘,且避免了繁雜的后處理工作。
2.1 Elman 神經網絡
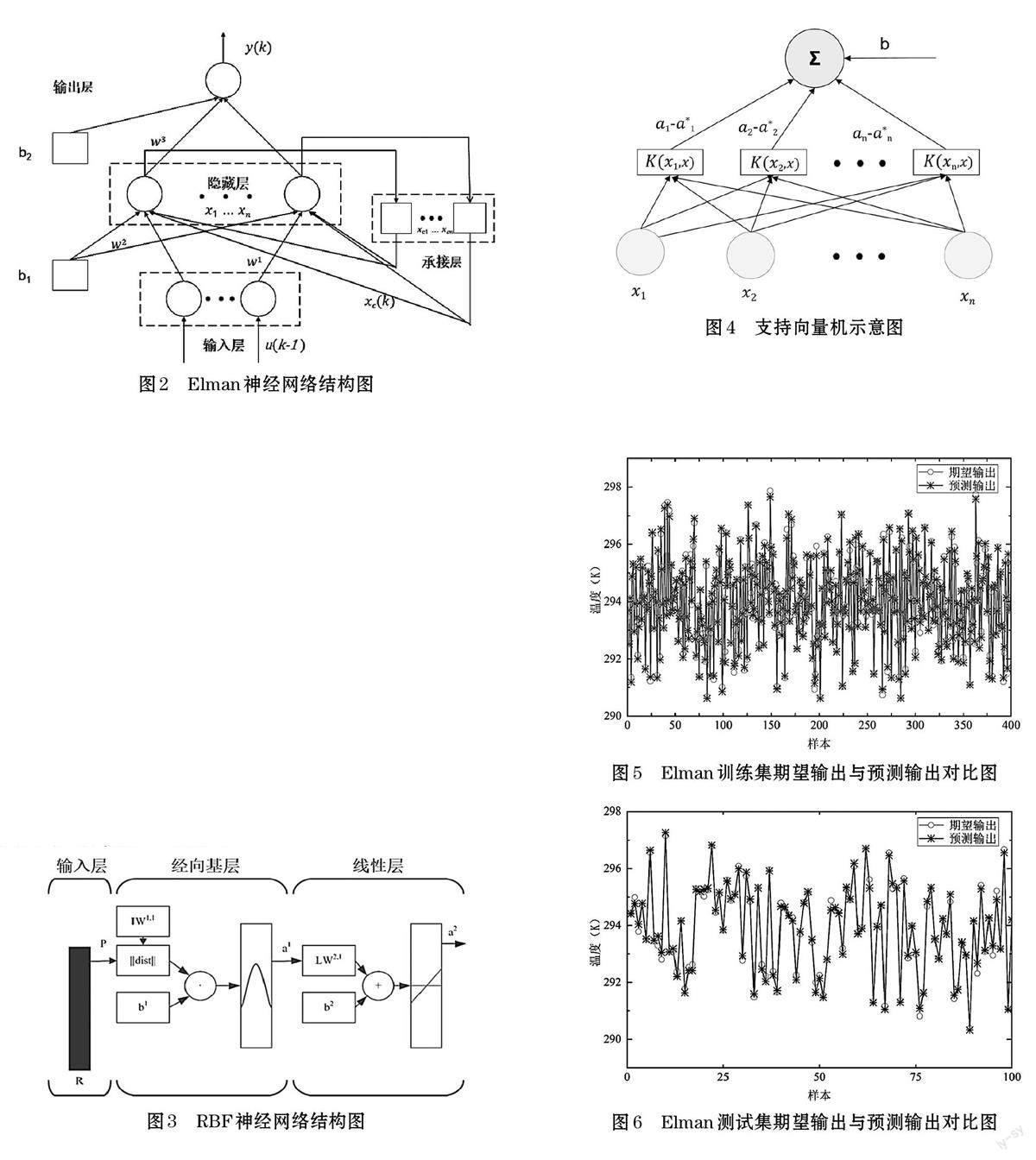
Elman 神經網絡特點是其在隱含層中添加了一個可進行一步延時的承階層[12],承接層將隱含層的輸出進行延時與儲存,并在下一時間步將其傳遞到隱含層的輸入,使其對歷史數據具有敏感性,從而使網絡可以適應時變特性[13]。Elman 神經網絡結構如圖2 所示。
2.2 RBF 神經網絡
本文使用的RBF 基于MATLAB 神經網絡工具箱,該神經網絡由三個層組成包括輸入層,由隱藏層神經元構成的徑向基層和由輸出層神經元組成的線性輸出層,構建函數newrbe 可建立精確徑向基神經網絡,與常用的中心選取方法不同,該函數直接將樣本作為中心,并將第一層權值設置為輸入向量的轉置向量。其網絡結構如圖3 所示。
2.3 SVR 支持向量回歸
支持向量機是一種監督學習的機器學習模型,它用分類算法來解決二分類問題,可利用已經標記了類別的訓練集來訓練SVM 模型,然后用它來對新的文本進行分類。支持向量機的分類問題求解思路是先將樣本映射到一個特征空間內,基于間隔最大化的原則在特征空間內找到一個超平面對樣本進行分割,對于多元分類問題,可將其分解為多個二分類問題進行分割。支持向量機結構如圖4 所示。
3 訓練及預測結果評價分析
3.1 Elman 神經網絡預測結果分析
使用Elman 神經網絡對空調回風溫度進行預測,隱含層神經元數量設置為58 個,承接層神經元數量為1 個,epochs 設置為10000 次,學習率設置為0.1,由圖5可知在訓練集的期望輸出與預測輸出吻合較好,但在某些樣本點仍有一定程度的誤差。由圖6 可知在測試集與訓練集的誤差情況大致相同,但在某些點仍有一定程度的誤差,沒有出現過擬合。Elman 預測性能指標見表3。
由表3 可知Elman 神經網絡表現出了很強的預測能力,訓練集和測試集的均方根誤差分別為0.11424K和0.13722K,遠低于0.5~1K 的測量不確定度,訓練集和測試集的最大誤差分別為0.40172K 和0.3526K 說明Elman 神經網絡對某些點的擬合情況不夠理想,但精度均在可接受范圍內,Elman 神經網絡的訓練時間約為11 秒。
3.2 RBF 神經網絡預測結果分析
使用MATLAB 中的精確徑向基神經網絡對空調回風溫度進行預測,結果如圖7 所示。
由圖7 可知,訓練集的期望輸出與預測輸出吻合較好,沒有觀測到有明顯誤差的樣本。由圖8 可知,測試集的期望輸出與預測輸出吻合情況與訓練集相似,沒有觀測到有明顯誤差的樣本,沒有出現過擬合。RBF 神經網絡的預測性能指標見表4。
由表4 可知,RBF 神經網絡表現出了很強的預測能力,訓練集和測試集的均方根誤差分別為0.04937K和0.05713K,訓練集和測試集的最大誤差分別為0.16601K 和0.21838K,均方根誤差與最大誤差均遠低于0.5~1K 的測量不確定度,在空調回風溫度預測的問題中RBF 神經網絡的精度明顯優于Elman 神經網絡,此外RBF 神經網絡還有更快的學習速度,訓練用時1.56 秒。
3.3 SVR 預測結果分析
使用基于MATLAB 的SVR 工具箱中的RBF 核函數SVR 模型對空調回風溫度進行預測,由圖9 可知SVR 預測模型訓練集的期望輸出與預測輸出吻合較好,沒有觀測到有明顯誤差的樣本。由圖10 可知測試集的期望輸出與預測輸出吻合情況與訓練集相似,精度較高,沒有出現過擬合。SVR 預測性能指標見表5。SVR 預測性能指標見表5。
使用基于RBF 核函數的支持向量回歸機的預測結果各項數據均優于RBF 與Elman 神經網絡,訓練集和測試集的均方根誤差分別為0.0437K 和0.0481K,訓練集和測試集的最大誤差分別為0.0.07863K 和0.13206K,均方根誤差與最大誤差均遠低于0.5~1K 的測量不確定度,在空調回風溫度預測的問題中SVR 表現出了比神經網絡更高的精度,此外支持向量回歸機有比神經網絡更快的學習速度,訓練用時0.86 秒。
3.4 機器學習模型訓練效果分析
由三種模型的模擬結果可知,在三種模型中Elman模型計算時間最長精度最差,RBF 模型計算時間大幅減少同時精度也有所提高,SVR 模型表現最佳,有最短的計算時間和最高的精度。從網絡結構上看Elman 神經網絡常用結構為四層,在隱含層增加一個承接層,RBF 神經網絡只有一個隱含層,并且輸入層到隱含層單元之間為直接連接,RBF 神經網絡的結構更加簡單,需要確定的模型參數更少。從訓練方式上看,Elman神經網絡需要確定的參數是連接權值和閾值,主要的訓練算法為BP 算法或改進的BP 算法;RBF 神經網絡可以動態確定隱含層單元數、數據中心和擴展常數等參數,訓練算法支持在線和離線訓練,有較強的輸入和輸出映射功能,并且理論證明在前向網絡中RBF 網絡是完成映射功能的最優網絡。RBF 神經網絡從隱層空間到輸出層空間的變換是線性的,這樣可以有效地降低計算復雜度內存消耗。因此,從理論上來說,RBF 神經網絡具有更快的學習速度、更好的逼近性能、更優的泛化能力、更簡單的結構參數學習等優點。
與RBF 神經網絡和Elman 神經網絡相比,SVR 結構更簡單,參數更少,SVR 只需要在輸出層進行誤差反向傳播和權重更新,而RB 神經網絡需要在每個隱含層都進行誤差反向傳播并根據梯度下降法進行權重更新,因此SVR 的訓練過程更簡潔,計算量更小。此外數據中心內部熱參數具有較強的相關性,所以不必使用結構較復雜的神經網絡,使用SVR 即可實現數據中心熱參數的準確快速預測。SVR 相比于RBF 神經網絡和Elman 神經網絡,不需要確定隱含層的結構和數量,也不需要進行復雜的誤差反向傳播算法,訓練過程更加簡單和高效,SVR 可以有效地處理高維數據和小樣本數據,而不會出現維數災難或過擬合問題且SVR 可以通過調整核函數、懲罰參數和松弛變量等超參數,來控制模型的復雜度和精度,具有較強的靈活性和魯棒性。
4 結論
通過參數化CFD 仿真建立不同機柜負載率下空調回風溫度的數據集,分別使用Elman 神經網絡、RBF神經網絡與SVR 支持向量回歸機對數據中心穩態運行情況下的空調回風溫度進行預測,三種模型均在短時間內實現了較為準確的預測。在三種機器學習模型中,SVR 支持向量回歸機憑借其訓練過程更簡潔,計算量小的優勢成為精度最高、訓練速度最快的機器學習模型,均方根誤差為0.048K,訓練時間為0.86s。原因是數據中心負載率與空調回風溫度具有較強的關聯性因此并不需要復雜結構的神經網絡即可建立快速預測模型,因此結構簡單、泛化能力強的SVR模型更具有優勢。

