基于數字孿生的液壓支架姿態監測
楊崇浩,白國長
(鄭州大學機械與動力工程學院,河南鄭州 450001)
0 前言
煤炭作為能源結構的重要組成部分,其開采過程環境惡劣、危險性高,因此迫切需要實現智能化開采[1]。液壓支架作為綜采工作面的支護設備,為整個綜采工作面的安全可靠運行提供了重要保障,液壓支架的姿態對其承載能力以及結構的穩定性具有很大的影響,因此對液壓支架姿態的可靠監測是實現煤炭智能化開采的前提[2]。
液壓支架的姿態主要包括其頂梁和底座的姿態。近年來,國內外許多學者對液壓支架姿態的監測方法進行了相關研究。陳冬方、李首濱[3]引入4個雙軸傾角傳感器,實現對液壓支架頂梁高度的監測。廉自生等[4]利用Zigbee技術構建液壓支架姿態監測網絡,實現液壓支架姿態的全面感知。胡相捧、劉新華[5]建立液壓支架姿態與驅動千斤頂的一一映射關系,實現初撐階段液壓支架頂梁和底座姿態的監測。任懷偉等[6]利用深度視覺技術實現液壓支架姿態的精準感知與動態監測。
數字孿生作為一種將現實空間的物體精確地映射到虛擬空間的技術,自2003年由GRIVES教授提出以來逐漸得到了廣泛的應用,尤其在狀態監測方面[7]。DAN等[8]通過構建基于機器視覺融合的數字孿生模型實現了橋梁交通載荷的監測。XIE等[9]通過構建基于物理與虛擬數據融合的數字孿生模型實現了刀具狀態的監測。WANG等[10]構建基于數據融合和Bi-LSTM網絡的數字孿生模型,實現了光通信過程的狀態監測和故障診斷。LIU等[11]構建基于虛實融合和LSTM網絡的數字孿生模型,實現了渦扇發動機的狀態監測。ZHOU等[12]構建基于傳感器數據和OPC UA信息模型的數字孿生模型,實現了港口起重機的狀態監測。數字孿生模型的構建方法目前尚不統一,其中TAO等[13]提出的由物理實體、虛擬實體、數據、連接和服務組成的五維模型應用較為廣泛。
結合數字孿生技術在其他領域的應用情況,發現現有的基于傳感器數據和圖像的液壓支架姿態監測方法主要存在以下問題:(1)傳感器數據折線圖和監控圖像對姿態的表示不夠直觀;(2)傳感器及監控數量有限,很難反映支架的整體姿態;(3)受地下環境和數據傳輸條件的影響,監測的圖像質量差、可靠性不強。本文作者基于信息融合技術,提出一種用于液壓支架姿態監測的五維數字孿生模型的構建方法,以實現液壓支架姿態的全面監測和異常預警,具體開發框架如圖1所示。
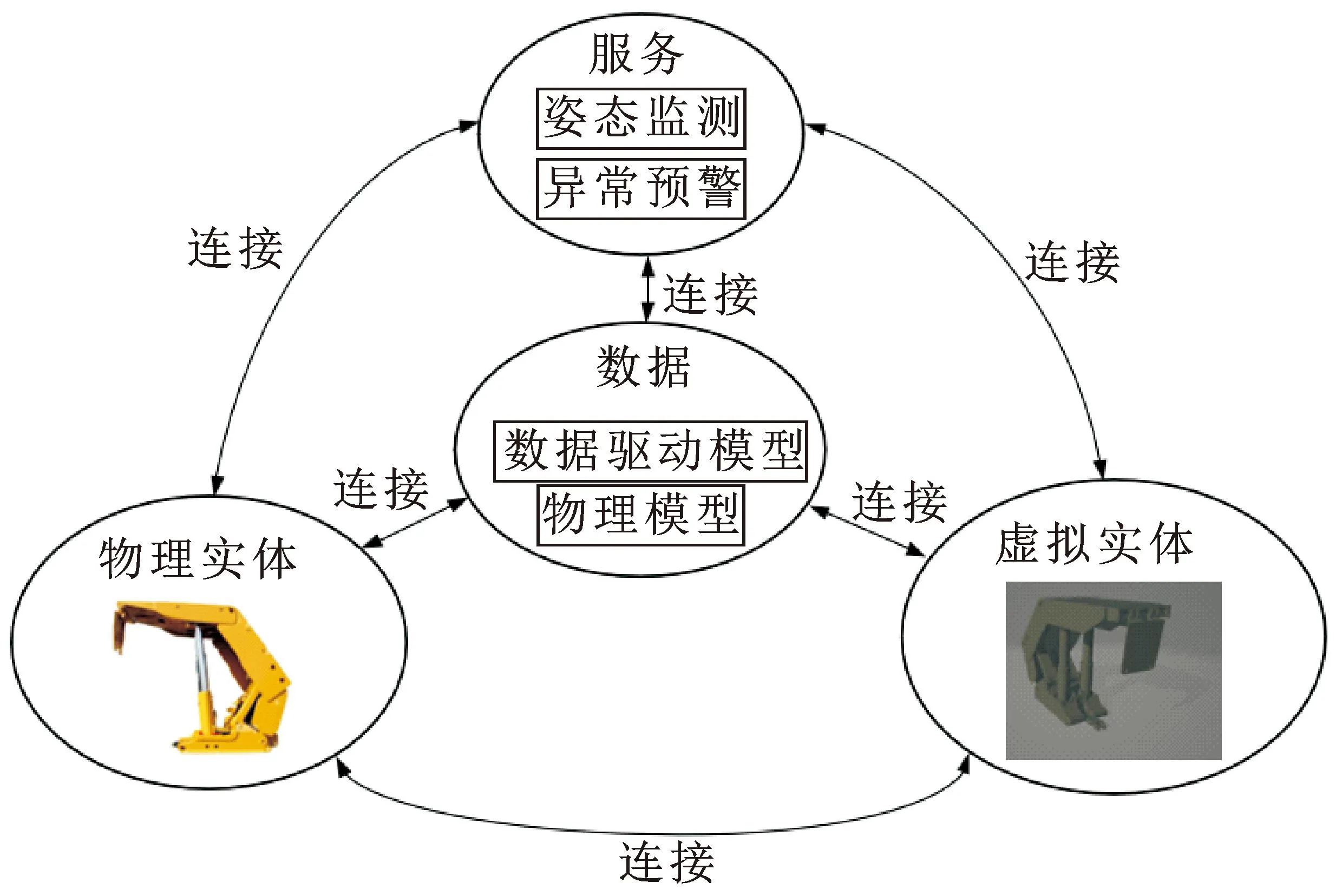
圖1 液壓支架數字孿生模型開發框架
1 液壓支架姿態監測的數據驅動模型
1.1 液壓支架姿態的表示與解算
液壓支架的姿態數據通過其頂梁和底座所安裝的慣性測量單元(Inertial Measurement Unit,IMU)進行采集,在慣性測量中,為了描述質點的位置以及運動情況,需要選擇相應的坐標系。液壓支架的載體坐標系O-xyz如圖2所示,圖中位置1處為IMU。
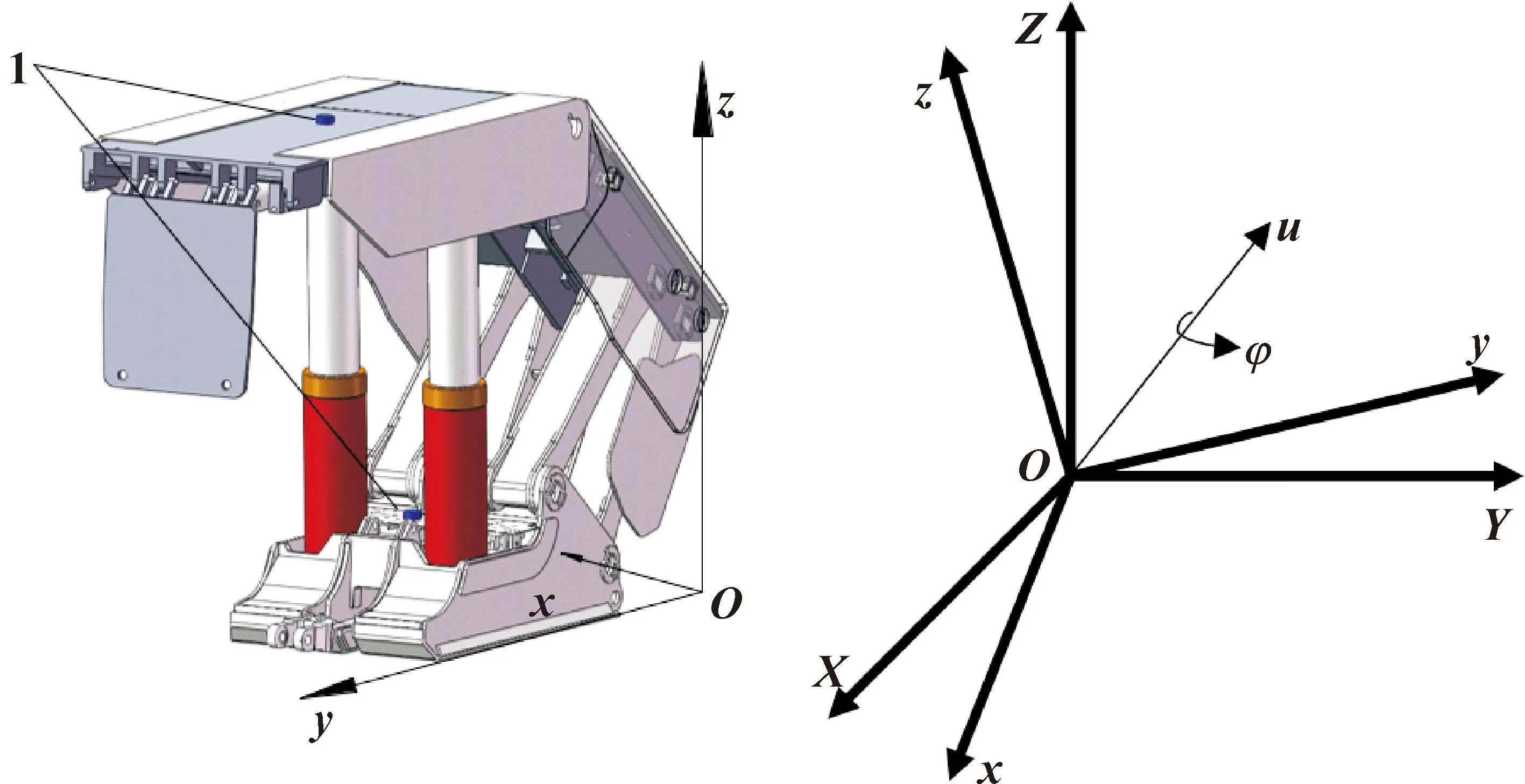
圖2 液壓支架的載體坐標系
文中以液壓支架的體坐標系O-xyz為載體坐標系,以東北天坐標系O-XYZ為參考坐標系。初始狀態時,兩坐標系重合,當液壓支架姿態變化后,載體坐標系可以理解為由參考坐標系依次繞z、x、y軸內旋得到。坐標系之間的轉換關系如圖3所示。
在慣性測量中,為了更好地表示角度的變化,并考慮到計算過程對硬件資源的占用,通常采用四元數法來進行姿態的求解。四元數定義為
(1)
式中:q0、q1、q2、q3為實數;i、j、k為與載體坐標系基相一致的標準正交基;u和φ分別為載體坐標系相對參考坐標系旋轉軸的單位矢量和旋轉角度。
由四元數的轉動定理及四元數的運算法則可得參考坐標系到載體坐標系的坐標轉換關系的四元數表達為
(2)
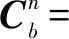
可得橫滾角γ、俯仰角θ與四元數的關系為
(3)
1.2 液壓支架姿態的測量算法
在使用IMU采集液壓支架姿態數據時,由于陀螺儀存在零偏及環境變化會引起隨機誤差,且這些誤差會隨積分逐漸積累,導致所測長期數據的精度降低;而加速度計容易受到振動和非重力加速度的影響,從而導致所測短期數據的精度降低。文中以加速度計的數據為觀測量,以陀螺儀的數據為預測量,通過卡爾曼濾波融合2組數據以得到更精確的液壓支架姿態。
液壓支架姿態的慣性測量系統可近似為線性系統,其狀態和觀測方程為
(4)
式中:xk為k時刻系統的狀態向量;yk為k時刻系統的觀測向量;A為狀態轉移矩陣;H為觀測矩陣;ωk-1為系統噪聲;vk為觀測噪聲。
在液壓支架姿態的實際測量中,建立系統的狀態更新方程:
(5)
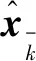
系統的量測更新方程為
(6)

1.3 液壓支架姿態的數據驅動模型
在液壓支架姿態測量系統中,通過卡爾曼濾波處理后的姿態數據可以建立平穩時間序列對液壓支架的姿態進行描述,考慮到序列具有較強的周期性,液壓支架姿態監測的數據驅動模型可以選擇自回歸滑動平均模型進行描述,形式如下:
xk=ψ1xk-1+ψ2xk-2+…ψpxk-p+εk+
θ1εk-1+θ2εk-2+…+θqεk-q
(7)
式中:xk為k時刻液壓支架的姿態值;ψ1、ψ2、ψp為自回歸模型的參數;{εk}為高斯白噪聲;θ1、θ2、θq為滑動平均模型的參數。
由于遞推最小二乘法方法具有計算量小、收斂速度快等優點。構建模型參數遞推狀態方程,通過遞推最小二乘法及數據更新實現其在線更新。將式(7)轉換為最小二乘形式:
(8)
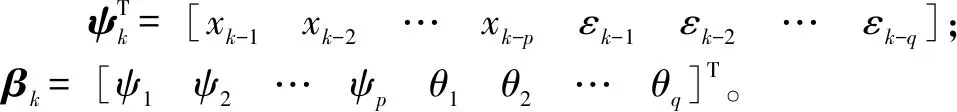
模型參數的遞推最小二乘法計算公式為
(9)
2 液壓支架姿態監測的物理模型
液壓支架數據驅動模型中的數據來源為相應的傳感器數據,然而安裝在液壓支架上的傳感器類型和數量有限,不能準確全面地反映液壓支架的工作狀態。液壓支架的物理模型可根據液壓支架的工作原理計算傳感器的未測量參數,以彌補測量參數的不足,從而在有限傳感器的前提下實現對液壓支架姿態的全面監測。液壓支架的物理模型主要包括其運動學模型、環境數據以及其物理實體的同步控制信號,通過上述模型的仿真得到液壓支架物理模型的姿態數據。
2.1 液壓支架的運動學模型
液壓支架的運動學模型主要用于模擬它在不同工況下各主要結構件的位置變化,在獲取傳感器數據的前提下實現對液壓支架姿態變化的全面分析。液壓支架姿態監測的二維運動學模型如圖4所示,以底座端點O為坐標原點,以水平方向為x軸,以豎直方向為y軸。
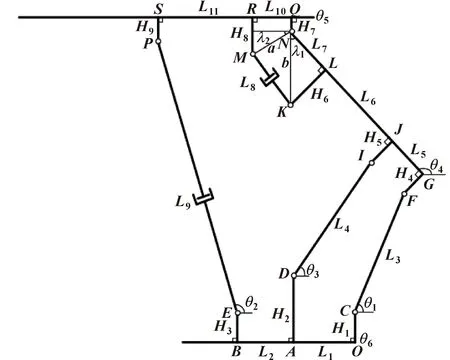
圖4 液壓支架的運動學模型
根據液壓支架的二維運動學模型及閉環矢量原理可構建液壓支架運動學方程為
-L1+L4cosθ3+H5sinθ4=L3cosθ1+H4sinθ4+
L5cosθ4
(10)
H2+L4sinθ3-H5cosθ4=H1+L3sinθ1-H4cosθ4+L5sinθ4
(11)
-L2+L9cosθ2-H9sinθ5+(L10+L11)cosθ5=
L4cosθ3+H5sinθ4+(L6+L7)cosθ4-H7sinθ5
(12)
H3+L9sinθ2+H9cosθ5+(L10+L11)sinθ5=
L4sinθ3-H5cosθ4+(L6+L7)sinθ4+H7cosθ5
(13)
(14)
圖4及公式(10)—(14)各參數的物理意義如表1所示。

表1 液壓支架運動學模型參數的物理意義
2.2 液壓支架的環境數據與控制信號同步
液壓支架的控制信號同步在文中主要是指同步立柱和平衡缸控制信號的數據,環境數據同步主要是指綜采工作面底板和頂板的起伏形態,以實現液壓支架姿態的解算和全面監測。在液壓支架設計尺寸已知的前提下,式(10)—(14)構成的方程組有7個未知數,分別為:θ1、θ2、θ3、θ4、θ5、L8和L9。當θ6的值變化時,θ1、θ2、θ3、θ4、θ5的計算結果要抵消相應的值。L8、L9可由液壓支架立柱和平衡缸的同步控制信號得到。因此剩余的5個參數θ1、θ2、θ3、θ4、θ5可由式(10)—(14)聯立求得。
3 液壓支架姿態監測的數字孿生模型
數據驅動模型隨著液壓支架的工作狀態變化而更新,對液壓支架姿態變化具有良好的適應性。但是數據驅動模型受數據的影響較大,對于歷史數據中沒有液壓支架姿態的,數據驅動模型由當前數據給出導致計算結果不合理。物理模型根據液壓支架的工作原理、環境數據以及同步控制信號得到液壓支架的姿態數據及其他傳感器未測量到的液壓支架姿態的理論數據,該數據準確性和適應性較差。因此文中采用長短期記憶(Long Short-Term Memory,LSTM)網絡對數據驅動模型和物理模型的數據進行處理,從而得到更為準確的液壓支架姿態信息。
在LSTM網絡中,通過大量學習數據驅動模型和物理模型來估計液壓支架的姿態信息作為數字孿生模型,LSTM網絡結構如圖5所示。
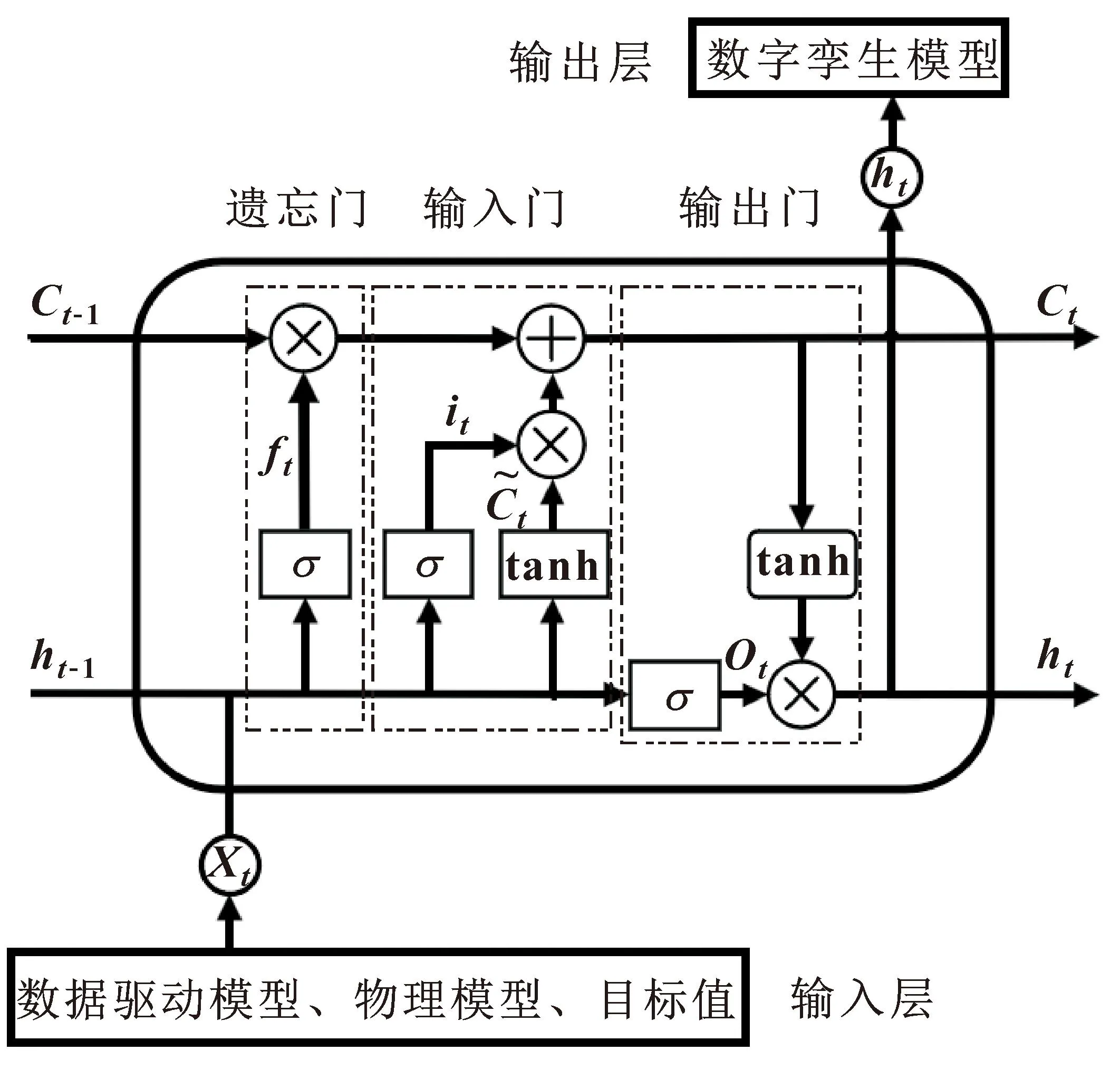
圖5 LSTM網絡結構
LSTM網絡設計了3個門,分別為遺忘門、輸入門和輸出門,用于控制LSTM網絡單元的狀態,其中:遺忘門決定Ct-1的哪些特征被計算Ct;輸入門決定加入多少新的信息;輸出門決定輸出什么值。在LSTM網絡單元中,門σ可以認為是一個sigmoid函數
σ(x)=1/(1+e-x)
(15)
遺忘門讀取ht-1和xt后輸出一個在[0,1]內的值與Ct-1中的數值相乘:
ft=σ(Wf·[ht-1,xt]+bf)
(16)
式中:σ表示sigmoid函數;Wf為遺忘門的權重矩陣;ht-1為上一個LSTM單元的輸出;xt為當前單元的輸入;bf為遺忘門的偏置項。
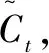
it=σ(Wi·[ht-1,xt]+bi)
(17)
(18)
式中:tanh是狀態激活函數。
輸出門首先通過門σ決定將哪些信息輸出,然后將單元狀態通過tanh層處理,最后結合2個部分確定單元的輸出:
ot=σ(Wo[ht-1,xt]+bo)
(19)
ht=ot⊙tanh(Ct)
(20)
由圖5可知,LSTM網絡輸入層包括三部分:數據驅動模型、物理模型的數據和以高精度傾角傳感器數據為參照的目標值。輸出層作為數字孿生模型的數據來源。LSTM網絡訓練的目的是優化輸入數據的權重使輸出數據更好地擬合目標值,其中,優化器函數是快速收斂的Adam梯度下降算法,超參數范圍通過仿真確定。
4 實驗與結果分析
4.1 實驗系統的建立
搭建液壓支架姿態監測系統,主要由液壓支架、乳化液泵站、液壓支架控制器、上位機、GY-521型IMU以及高精度傾角傳感器組成。
4.2 評價指標
在誤差值的各評價指標中,均方根誤差(Root-Mean-Square Error,RMSE)對異常值更敏感,因此文中以均方根誤差為液壓支架姿態估計的評價指標,用于衡量估計值與目標值之間的偏差,用公式表示為
(21)
式中:ypi為液壓支架姿態的估計值;yi為液壓支架姿態的目標值。
4.3 實驗結果
以高精度傾角傳感器的值為目標值,對比并分析液壓支架在“升架”過程中IMU數據、數據驅動模型、物理模型和數字孿生模型數據的有效性,如圖6—9所示。

圖6 IMU的卡爾曼濾波
圖6所示為液壓支架“升架”過程中安裝在頂梁和底座的IMU數據經過卡爾曼濾波的處理結果。可得:卡爾曼濾波處理后的IMU姿態數據中,頂梁俯仰角與目標值的RMSE最大,為0.245 1°;底座橫滾角與目標值的RMSE最小,為0.028 4°,且2組數據整體擬合度較好,可以滿足監測系統的要求。
圖7所示為液壓支架姿態監測數據驅動模型的數據處理結果。可知:液壓支架姿態監測數據驅動模型的數據中,頂梁俯仰角與目標值的RMSE最大,為0.281 4°;底座橫滾角與目標值的RMSE最小,為0.026 5°,且2組數據整體擬合度較好,可以滿足監測系統的要求。
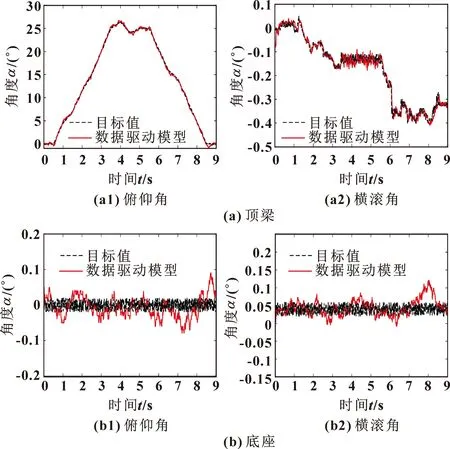
圖7 數據驅動模型的支架姿態監測曲線
圖8所示為液壓支架姿態監測物理模型的數據處理結果。可知:液壓支架姿態監測數據驅動模型的數據中,頂梁俯仰角與目標值的RMSE最大,為0.847 2°;底座橫滾角與目標值的RMSE最小,為0.011 4°,其中頂梁姿態的2組數據擬合度較差,不符合檢測系統的要求。

圖8 物理模型的支架姿態監測曲線
圖9所示為液壓支架姿態監測數字孿生模型的數據處理結果。可知:液壓支架姿態監測數據驅動模型的數據中,頂梁俯仰角與目標值的RMSE最大,為0.245 4°;底座俯仰角與目標值的RMSE最小,為0.019 1°,相較于支架姿態監測的數據驅動模型和物理模型監測性能均有不同程度的提升,且2組數據整體的擬合度較好,提高了支架的姿態監測性能。
以頂梁俯仰角為例,圖10所示為當前液壓支架姿態出現歷史數據中沒有的液壓支架異常姿態時各模型的支架姿態監測曲線。可知:在出現歷史數據中沒有的異常數據時,數據驅動模型與目標值的RMSE為0.510 2°;物理模型與目標值的RMSE為0.507 7°,在7.8 s出現異常姿態后數據驅動模型的數據與目標值擬合度較差,物理模型的數據與目標值整體擬合度較差,對支架的監測能力較弱。數字孿生模型與目標值的RMSE為0.269 5°,且整體擬合度較好,可以滿足監測系統的要求,提高了支架姿態監測結果的可靠性。
5 結論
文中針對現有液壓支架姿態監測所存在的問題,以液壓支架“升架”過程為例,通過信息融合、數據驅動等方法,構建了用于液壓支架姿態監測的數字孿生模型,并通過實驗驗證了該方法的有效性。該方法可以實現液壓支架姿態的全面、可靠監測,并可用于姿態的異常預警;同時為數字孿生模型的構建以及液壓支架的姿態監測提供參考。

