基于DRHOSVM的復雜結構瞬態可靠性分析

殷銳，費成巍

(1.西安明德理工學院智能制造與控制技術學院，陜西西安 710124；2.復旦大學航空航天系，上海 200433)

0 前言

可靠性分析對復雜結構的優化設計和可靠運行至關重要。復雜結構是機械關鍵部件不可缺少的，其性能受惡劣的工作環境和復雜的載荷條件的影響。 由于高維不確定因素，復雜結構在瞬態極值輸出響應階段容易出現故障，影響機械的使用性能。為了保證機械的安全，有必要進行復雜結構受高維輸入參數影響時的瞬態可靠性分析。

根據結構可靠性分析國內外現有進展，可將其研究方法分為數值模擬法、近似解析法和代理模型法。數值模擬方法主要涉及隨機抽樣[1-3]和重要度抽樣[4-6]。 隨機抽樣方法廣泛應用于分析結構可靠性，在隨機失效中也應用廣泛。 然而，由于大量樣本函數的局限性，隨機抽樣方法所消耗的計算成本難以承受。 在重要性采樣方法中，可以將原始概率密度函數替換為重要性采樣密度函數，以減少樣本數量[7]。 由于難以在高維空間中構建合適的ISD函數以及時變特征，該方法的應用范圍仍受限。因此，數值模擬方法的可行性在復雜結構瞬態可靠性分析中較低。

在近似分析方法中，矩方法因可接受的精度和效率而被廣泛應用于可靠性分析，包括一階和二階矩法[8-11]和點估計方法[12]。但近似解析方法不適于解決功能函數未知的可靠性問題，且可靠性分析方法可能會產生涉及高度非線性功能函數的不穩定解。因此，在復雜結構函數未知的情況下，近似解析方法的應用也受到限制。

代理模型方法的出現有效克服了數值模擬法和近似解析法的不足，為結構瞬態可靠性分析開辟了新的研究方向[13-16]。其中，支持向量機 (Support Vector Machine，SVM)是一種廣泛應用的回歸代理建模工具。 SVM 回歸的主要思想是在擬合層上擬合盡可能多的樣本，同時限制邊緣違反程度[17-18]。由于最小化回歸誤差和自動選擇機制的特性，它對于復雜的中小型數據集的可靠性分析更有效率。韓彥彬等[19]提出了一種在柔性機構中進行高效、高精度動態可靠性分析的SVM回歸極值方法。HU等[20]提出了一種新的一類 SVM 回歸方法來適應偏差約束。在結構概率的分析中，由于需要考慮不同且多樣的運行載荷，導致數據樣本稀疏，在高維輸入參數的情況下計算困難。在這種情況下，降維(Dimension Reduction，DR)策略是緩解維數災難的重要途徑。DR方法包括線性DR和非線性DR。在線性DR方面，LIU等[21]探索了一種基于主成分分析的全局代理模型技術。 KIM等[22]開發了線性判別分析來獲取基于廣義LDA方法的多類分類器。線性DR雖然可以提取主要信息，但難以處理大計算量和混合數據。在非線性DR中，DAS NEVES CARNEIRO和CONCEI?O ANTNIO[23]提出了基于Sobol′指數近似局部解的不確定空間解析降維技術，以解決可靠性的魯棒設計優化問題。ZHOU、PENG[24]提出了一種結合核主成分分析(Kernel Principal Component Analysis，KPCA)和高斯過程回歸代理模型的可靠性方法。與線性DR方法相比，非線性DR方法由于流形和核方法的存在，可以有效處理高維數據的分布問題，從而提高計算效率和降維效果。因此，可采用非線性DR對高維參數下的復雜結構數據集進行降維分析，以提升SVM在高維數據集的應用效率。

SVM模型的效率和精度主要由模型中的超參數決定。為了優化相關的超參數，許多學者研究了智能優化算法。JIA等[25]利用粒子群優化算法改進了SVM核函數的參數，以獲得最高的識別和定位精度。HESAMI、 JONES[26]基于遺傳算法(Genetic Algorithm，GA)提出了SVM-GA來優化SVM模型。ZHOU等[27]通過灰狼優化、鯨魚優化算法和飛蛾火焰優化3種算法優化SVM模型的超參數。從以上研究來看，智能優化算法與傳統的支持向量機相比確實提升了性能。然而，智能優化算法存在一個可改進的缺陷，即得到的優化值容易陷入局部優化。在某些情況下，局部最優解比全局可行解表現更差，導致SVM 性能降低。因此，迫切需要開發一種新的優化策略來尋找最優參數并提高準確性和效率。

針對上述結構可靠性分析問題，本文作者提出一種新的代理建模方法，即基于降維策略的參數優化支持向量機算法(Hyperparameters Optimization Support Vector Machine-based on Dimensionality Reduction，DRHOSVM)。 DR策略以保持高低維線性關系為約束，將大規模輸入變量嵌入高維空間，拓寬傳統支持向量機的高維使用范圍。參數優化以相似性密度和個體最優為目標，獲得傳統支持向量機的最優超參數，改善受超參數影響的算法精度。 以航空發動機渦輪葉盤疲勞壽命數據集為研究案例，證明所提出的DRHOSVM在高維參數下的復雜結構瞬態可靠性分析中的有效性。

1 基于DRHOSVM的復雜結構瞬態可靠性分析

1.1 基于DRHOSVM的復雜結構瞬態可靠性分析流程

在復雜結構瞬態可靠性分析中，由于其功能函數以隱式函數的形式存在，導致采用數值模擬和近似解析法時計算性能低下。為滿足工程精度和效率兩方面的要求，SVM可在中小樣本量的基礎上擬合顯式功能函數代替原有隱式函數。在此基礎上，結合瞬態極值思想，采用SVM將動態輸出響應過程轉化為極值輸出響應過程。然而，SVM在擬合復雜高維非線性問題時存在性能失真問題。DR策略和參數優化的出現為解決這一問題提供了可行的方案。一方面，降維策略在保持高、低維數據空間線性關系不變的同時，將高維數據嵌入低維數據，以避免維數災難引起的算法效率和精度問題。另一方面，參數優化以相似性密度和個體最優相結合的方式獲取SVM的最優超參數，以產生最優模型下的高精度可靠性分析結果。因此，以降維策略為輸入參數處理方案，SVM為建模基礎，參數優化為最優模型搭建基礎，提出DRHOSVM以解決高維變量下的復雜結構瞬態可靠性分析問題。基于DRHOSVM的復雜結構瞬態可靠性分析流程如圖1所示。

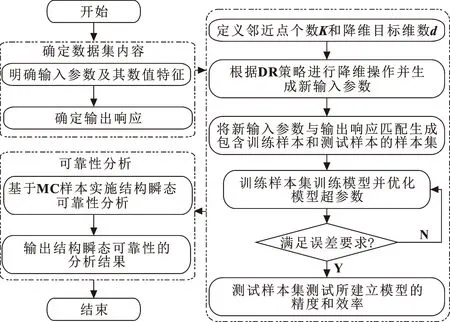
圖1 基于DRHOSVM的復雜結構瞬態可靠性分析流程

1.2 DRHOSVM數學模型推導

所提出的DRHOSVM通過在時域[0,T]內建立具有高可靠性和小誤差的數據模型，建立復雜結構的高維輸入參數與瞬態極值響應之間的關系，以執行可靠性分析。建立DRHOSVM模型的首要任務是獲取瞬態極值樣本。在獲取樣本階段，采用拉丁超立方抽樣(Latin Hypercube Sampling，LHS)方法，此方法在保證樣本的隨機性和相對均勻性的同時，提高了抽樣效率。所獲得樣本一方面作為有限元模擬的輸入，生成相應的瞬態極值輸出響應；另一方面作為DR的輸入，在保證高、低維局部線性關系的基礎上，對輸入參數進行降維處理，形成與瞬態極值輸出響應匹配的低維輸入變量，將新輸入變量與輸出響應結合可生成DRHOSVM的樣本集。樣本集分為訓練樣本集和測試樣本集，訓練樣本集被引入HOSVM以訓練具有最優超參數的最佳模型，測試樣本集用以檢驗所訓練的HOSVM的精度和效率。

所提出的DR策略是一種非線性降維方法，假設D維M個輸入樣本點X=[x1,…,xM]∈RD×M在規定區域內是線性的，即樣本點的數據可由區域內的k個預選點線性表示，遠離樣本點數據的多余點對局部線性關系沒有影響，該策略降低了DR的復雜度和計算量。

初始高維空間的樣本點X=[x1,…,xM]∈RD×M和k個預選點的線性關系可通過其均方誤差函數表示為

(1)

對于第i個變量xi，其歐幾里得距離用于計算整個區域中的所有可能點并升序排列，并選擇其中距離最短的k個鄰近點xij，j表示變量xi的鄰近點的標記數。

為保持高、低維空間的樣本點與鄰近點的線性關系不變，需在高維空間確定樣本點xi的線性重構系數βij，如式(2)所示：

(2)

式中：i、j、l、n和o皆為樣本點的標記。

假設降至d維的樣本仍保持與D維高維空間同樣的線性關系，必須保證其重構系數和鄰近點個數不變。因此，只需重構系數和鄰近點個數確定后，由xi映射到d維空間中樣本坐標uig，即

(3)

式中：uig代表低維映射樣本的第i行第g列。

通過DR策略的實施，原輸入樣本已由D維降至d維。需注意的是，由于線性重構系數的不變性，導致輸入樣本的維數降低時其包含的信息也保持不變。將新輸入樣本與極值輸出響應進行匹配形成模型樣本集，將樣本集分為訓練樣本集和測試樣本集。訓練樣本集用于建立模型，測試樣本集用以測試所建立模型的計算性能。模型中建立了輸入參數和輸出響應之間的回歸關系，其關系的準確性影響了復雜結構瞬態可靠性分析的有效性。SVM作為高效的代理模型，應用于回歸問題時具有相對較高的精度和效率。因此，選取SVM作為模型的建模基礎。

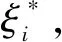
(4)

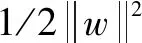
(5)

式(5)滿足卡羅需-庫恩-塔克(Karush-Kuhn-Tucker，KKT)條件，因此該原始優化問題可轉化為如式(6)所示的對偶問題。

(6)

(7)

將式(7)代入式(6)，原始優化問題的對偶形式可變化為

(8)

式中：m代表由DR策略形成的新樣本集個體數量；xj表示與xi不同的輸入樣本。

通過求解式(8)，SVM回歸函數可得到

(9)

為符合實際工程樣本的效率需求和協同DR策略，引入核函數用以代替式(9)中的輸入樣本內積xiTxj。核函數可表示為

k(xi,xj)=〈φ(xi)φ(xj)〉=φ(xi)Tφ(xj)

(10)

(11)

γ作為SVM回歸應用的另一重要超參數，它與高斯RBF的關系為

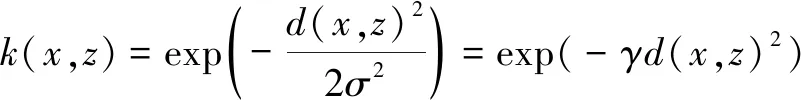
(12)

式中的γ確定了高斯函數的峰值，當γ越大，高斯函數峰值越大分布越密，SVM的支持向量越少；反之，γ越小，高斯函數峰值越小分布越散，支持向量的個數越多。支持向量是構建擬合層的必要要素。當γ的屬性反映在SVM回歸問題時，其值越大支持向量越少，SVM越容易過擬合。此時，訓練時的SVM模型性能優越，但測試性能低下。反之，γ越小的會導致SVM欠擬合。

通過上述分析，超參數C和γ共同影響了SVM回歸的泛化和預測能力。為精確地分析復雜結構的瞬態可靠性，有必要通過參數優化設計獲得SVM的最優超參數。GA作為啟發式尋優算法的代表方法，具有高效率和強魯棒性，適于SVM超參數尋優的參考算法。由于遺傳操作的不足，傳統的GA易于局部收斂。因此，為獲得SVM超參數的最優值，在傳統GA中進行遺傳操作的基礎上，提出考慮個體相似性密度最低和適應度最優兼具的參數優化算法。個體相似性密度計算如式(13)所示：

(13)

式中：η代表個體適應度；λ表示能容忍的個體適應度相似密度的臨界值。

使得相似性密度較小和適應度較大的參數相似性選擇兩方面兼具的個體形成新種群P(g)″可表示為

(14)

式中：f(ηi) 為第i個個體的適應度值；a和b分別為相似性密度和適應度值的偏向性系數。

新種群P(g)″個體數量只有原有個體數量的一半，因此下一代種群P(g+1)個體數量也同樣只產生一半，與新種群P(g)″融合形成g+1代的初始種群以進行下一次迭代計算。當迭代次數滿足預設迭代最大值時，參數優化停止，輸出具有全局最優值的超參數。

1.3 基于DRHOSVM的復雜結構瞬態可靠性分析

結合DRHOSVM的數學模型，復雜結構的極限狀態函數可建立，如式(15)所示：

h(u)=yallow-yDRHOSVM(u)

(15)

式中：yallow和yDRHOSVM(u)分別為復雜結構的瞬態極值允許值和經DRHOSVM推導的預測值。極限狀態函數是復雜結構的失效域與安全域的分界線，當h(u)≥0時復雜結構處于安全狀態，反之處于失效域。

通過DR策略，原有輸入樣本的均值和標準差可表示為v=[v1,v2,…,vM]和D=[D1,D2,…,DM]。則極限狀態函數的均值和標準差形如

(16)

此時，極限狀態函數服從高斯分布，其可靠度可表示為

(17)

2 航空發動機渦輪葉盤的瞬態可靠性分析

渦輪葉盤作為燃氣輪機的關鍵部件，用于承受進入燃燒室的高溫高壓氣流，以維持航空發動機的運行。葉片疲勞是航空發動機發生頻率較高的失效形式，也是發動機失效的主要原因。因此，采用所提出的DRHOSVM方法從疲勞壽命角度分析航空發動機渦輪葉盤的瞬態可靠性。

以航空發動機渦輪葉盤(如圖2所示)的1/46為研究對象，以其疲勞壽命瞬態極值數據集為案例樣本集，其輸入參數的均值和標準差見表1。假設輸入參數服從正態分布，且相互獨立。

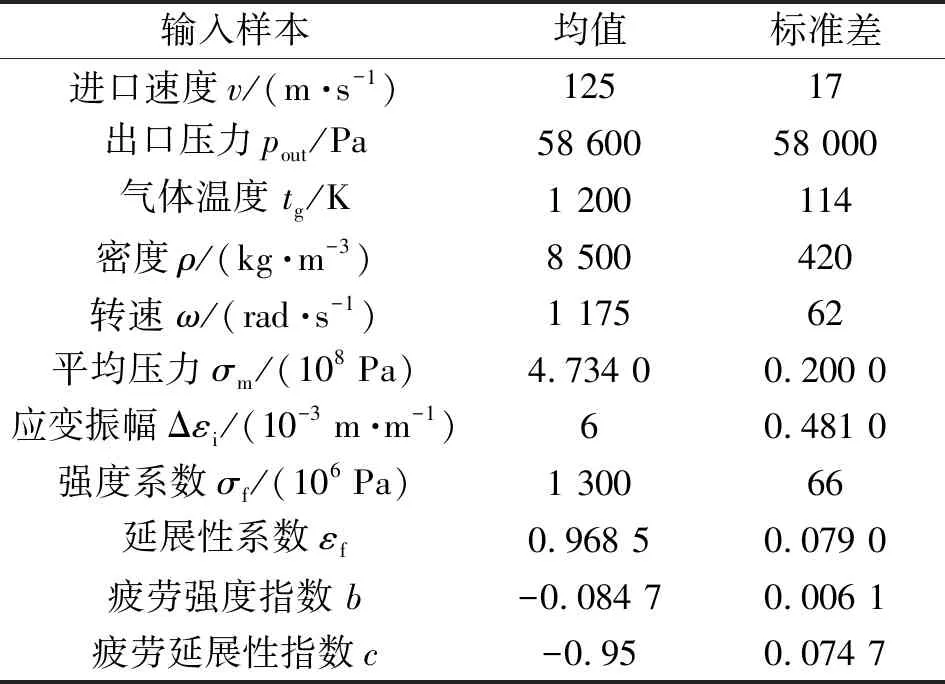
表1 輸入參數的數值特性

圖2 航空發動機渦輪葉盤

為建立渦輪葉盤的DRHOSVM模型，將數據集中包含的146組數據進行DR操作。將原11維的輸入變量降至5維，并保持其數據信息不缺失。降維后輸入樣本的均值和標準差見表2。

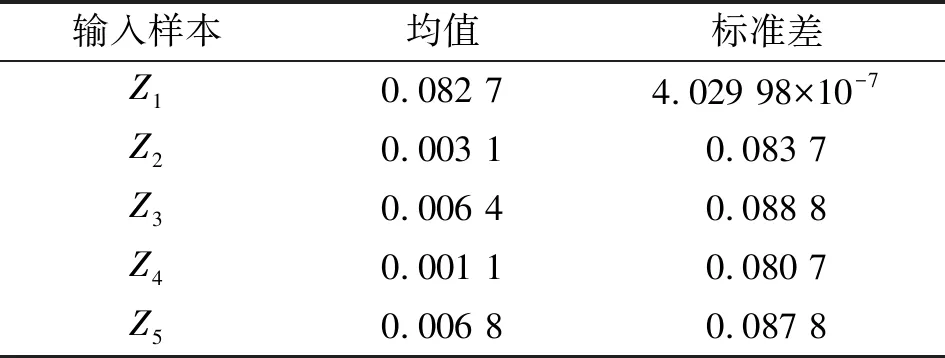
表2 降維后輸入參數的數值特性

選取前60組數據作為訓練樣本集，用于建立渦輪葉盤的DRHOSVM模型，后86組數據作為測試樣本集驗證建立好的DRHOSVM模型的有效性，有效性通過均方誤差(Mean Square Error，MSE)和R2說明。MSE評價數據的變化程度，其值越小，說明預測模型描述實驗數據的精確度越高。R2是擬合優度，反映模型對樣本數據的擬合程度，其值越接近1，擬合效果越好。所建立的DRHOSVM模型應用于測試樣本集的預測曲線，如圖3所示。

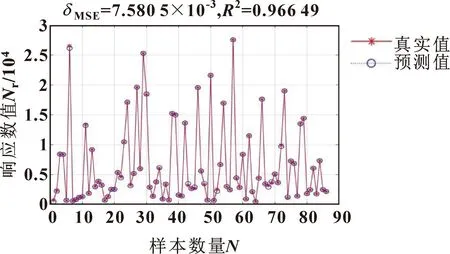
圖3 測試樣本的真實值與預測值

對于所建立的DRHOSVM，測試樣本集的MSE和R2分別為7.580 5×10-3和0.966 49，均處于回歸預測的有效域內。

基于復雜結構的瞬態可靠性分析原理，結合所驗證的DRHOSVM模型，執行渦輪葉盤的可靠性評估。如圖4、5所示，以10 000個MC(Monte Claro，蒙特卡羅)樣本為輸入，其疲勞壽命分布服從正態分布。通過統計分析，渦輪葉盤的最大允許疲勞壽命為2.200 6×104循環。

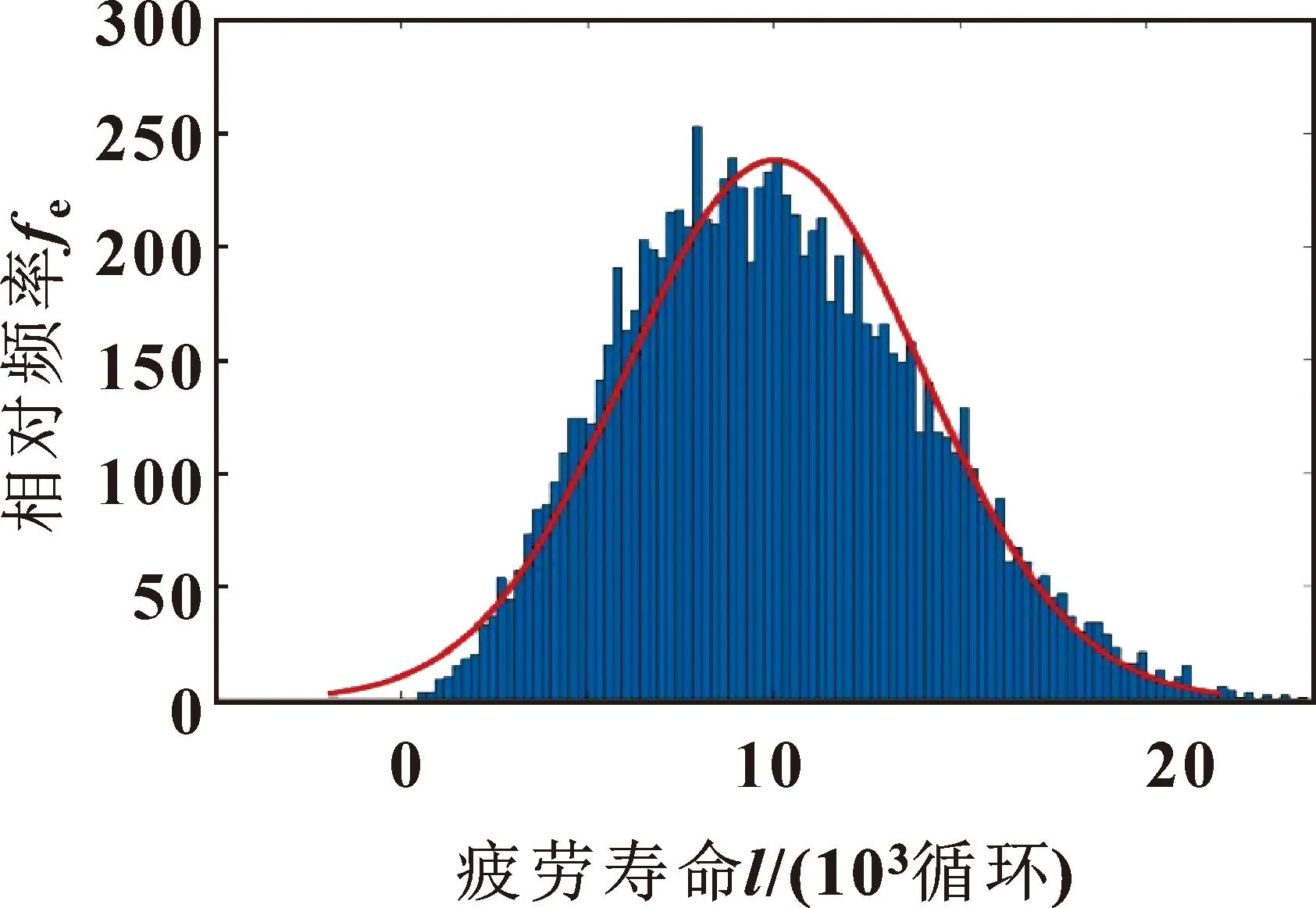
圖4 分布直方圖

輸入不同蒙特卡羅樣本時渦輪葉盤的可靠度見表3。可以看出：MC模擬次數越多，渦輪葉盤的可靠度越收斂。即越多的蒙特卡羅樣本有助于可靠度收斂值的確定。當最大允許疲勞壽命為2.200 6×104循環時，渦輪葉盤的疲勞可靠度為0.997 5。

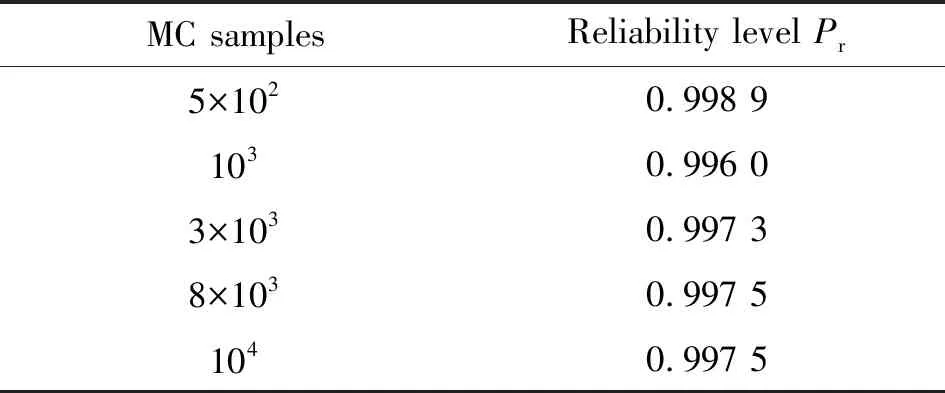
表3 降維后輸入參數的可靠度

3 DRHOSVM算法有效性驗證

以建模特性和模擬性能為驗證依據，以直接模擬、傳統支持向量機、Kriging作為比較對象，驗證所提出的DRHOSVM的有效性和適用性。

3.1 建模特性

基于相同計算條件和樣本集，通過與傳統支持向量機、響應面法的比較驗證了DRHOSVM的建模特性。對于航空發動機渦輪葉盤降維數據集，前60個樣本用于訓練DRHOSVM模型，其余86個樣本用于估計開發的DRHOSVM模型的建模誤差。針對其余比較算法，在渦輪葉盤疲勞可靠性建模時，采用未降維的原樣本集的后86個測試樣本，對前60個訓練樣本建立的相應模型。渦輪葉盤疲勞可靠性的不同建模方法的建模時間和建模誤差見表4。

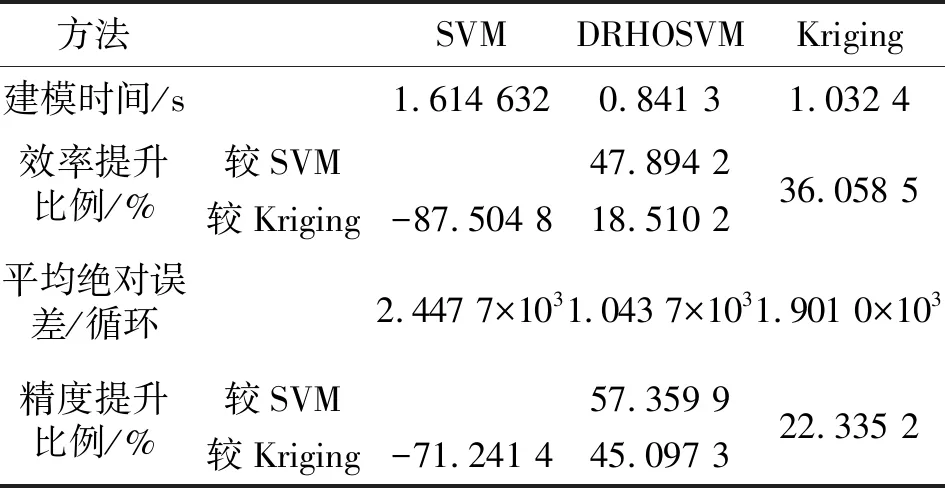
表4 SVM、DRHOSVM及Kriging的建模特性

相對于SVM和Kriging，DRHOSVM在建模效率和建模誤差上都表現最優，證明了DRHOSVM建模速度和建模精度的優越性。DRHOSVM在建模效率方面，較SVM提升了47.894 2%，較Kriging提升了18.510 2%。DRHOSVM在建模精度方面，較SVM提升了57.359 9%，較Kriging提升了45.097 3%。出色的建模特性不僅來自于DRHOSVM對高維數據進行了保留數據信息的降維處理，并且通過參數優化算法建立了最優模型。

3.2 模擬性能

在仿真性能方面，以直接模擬、SVM和Kriging作為比較方法，驗證應用于復雜結構瞬態可靠性分析的DRHOSVM的有效性。對于不同的MC樣本(5×102、103、3×103、8×103和104)，以直接模擬方法作為驗證中的評價指標，SVM、Kriging和所提出的DRHOSVM在模擬效率、可靠性水平和模擬精度方面的模擬性能，見表5、6。考慮到難以承受的計算負擔，104個蒙特卡羅樣本不應用于直接模擬方法。

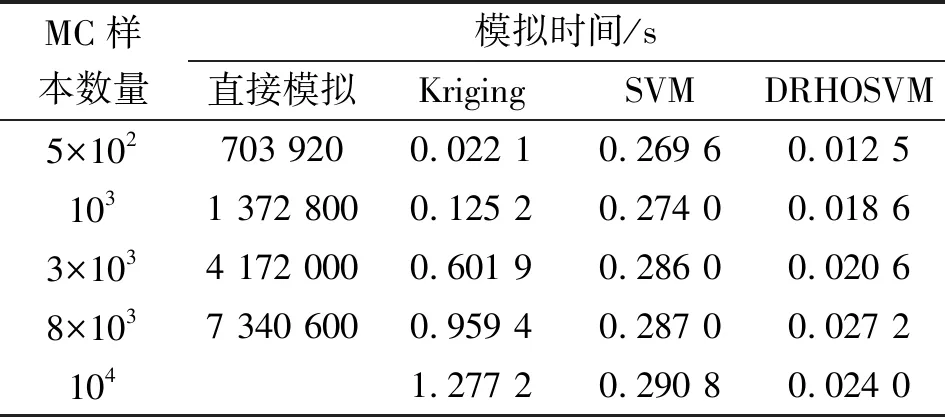
表5 不同蒙特卡羅樣本數量各方法的模擬時間

從表5可看出：DRHOSVM應用于5組不同的蒙特卡羅樣本時的模擬效率明顯高于其余方法。當蒙特卡羅樣本量為104時，DRHOSVM的模擬時間為0.024 0 s，SVM次之。DRHOSVM的高模擬效率是由于DR策略的實施將高維數據降至低維空間，使得計算難度和復雜度減小。

從表6可看出：DRHOSVM在可靠度和模擬精度上皆為4種方法的最優者。DRHOSVM的可靠度在MC樣本個數為8×103時收斂到穩定值0.997 5。以直接模擬方法結果作為比較依據，應用于渦輪葉盤疲勞可靠性分析的DRHOSVM的模擬精度達到99.989 9%，高于SVM和Kriging。原因為所提出的DRHOSVM采用了相似度密度和個體最優兼具的參數優化方法，以最優超參數建立了應用模型。因此，DRHOSVM具有較好的模擬特性。

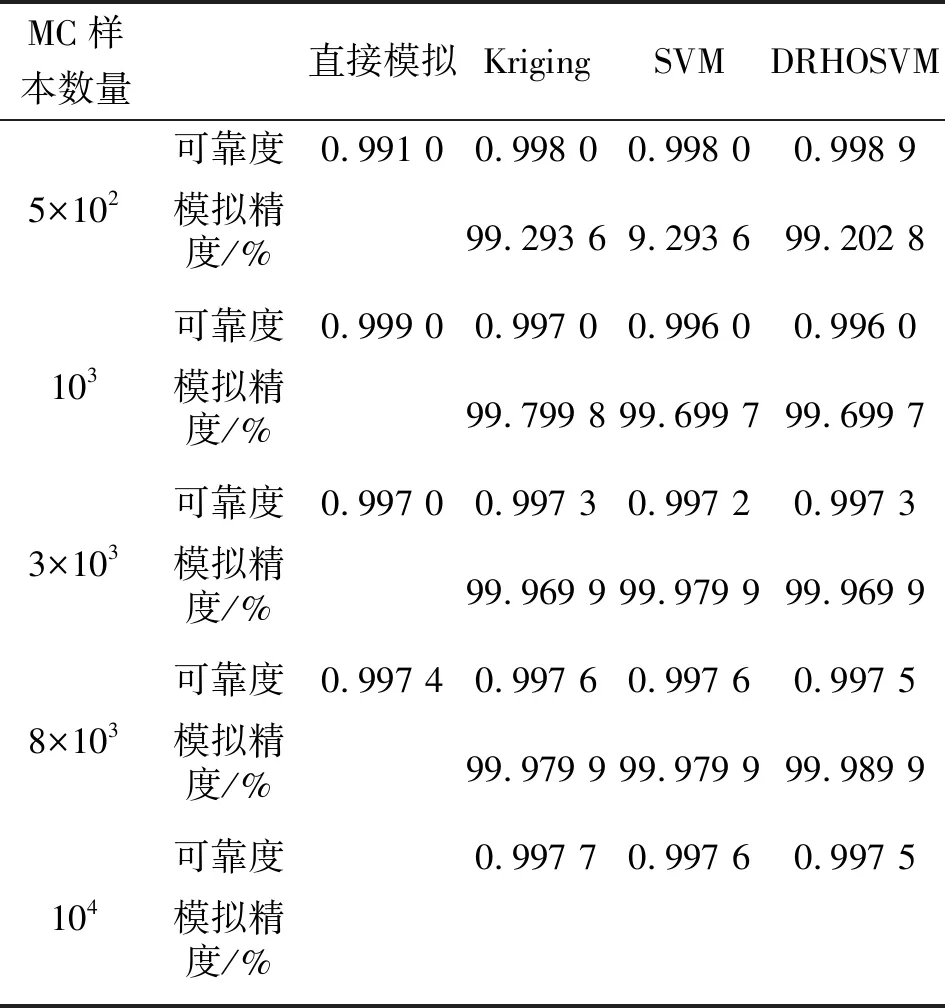
表6 不同蒙特卡羅樣本各方法模擬的可靠性水平和模擬精度

4 結論

通過引入DR策略和參數優化算法，提出DRHOSVM以提高傳統支持向量機SVM在復雜結構瞬態可靠性分析中的性能。在訓練和測試過程中，以航空發動機渦輪葉盤數據集作為對象。為檢驗所提出的DRHOSVM的性能，在建模特性和模擬特性方面與直接模擬、Kriging和SVM進行對比，可以得出：

(1)4種預測方法的誤差均在工程實際應用的接受的范圍內，與Kriging和SVM相比，DRHOSVM模型具有較高預測精度，所建立模型的平均絕對誤差為1.043 7×103循環。

(2)與其他方法相比，所提出的DRHOSVM在建模效率方面具有優勢。DRHOSVM所消耗的建模時間為0.841 3 s，低于Kriging模型和傳統的SVM模型。此外，DRHOSVM在模擬速度與建模時間方面同樣表現優秀，在104個蒙特卡羅樣本中，DRHOSVM以0.024 0 s完成模擬，這表明DRHOSVM在建模和仿真過程中兼具高效率。

所提出的DRHOSVM為復雜結構瞬態可靠性分析提出了可行的新思路，對于高維參數復雜結構的優化設計具有重要意義。