周向對稱零件分析模型及約束、加載方法研究

黃云霞 郭越江 竇柏通

（中國航發商用航空發動機有限責任公司，上海 200241）

0 引言

在工程中有很多構件，如車床的光桿、攪拌機軸、汽車傳動軸等，都是受扭構件。在使用有限元對這些受扭構件進行靜強度分析時，如果用整圈模型進行計算，約束及加載相對容易，但是網格數量大，需要的計算資源多；若網格數量少，則計算精度不夠。因此，一般采用扇形段模型來進行模擬，但扇形段模型的邊界條件和載荷施加方法不能按照整圈模型來加載。本文嘗試了各種整體模型和扇形段模型的約束及加載方法，為結構受力與變形分析提供依據[1]。

1 理論

扭矩是剛體發生扭轉變形的動力，扭矩實際上是一力偶矩。在實際分析過程中，將受扭構件一端約束，另一端施加扭矩。

在進行受扭構件靜力分析時，需要對受扭桿件的扭轉變形進行平面假設，即扭轉變形前后截面的大小形狀均不變，相鄰兩個截面間的距離不變。物理依據是剪切胡克定律，即剪應力和角應變成正比，系數為材料的剪切彈性模量。靜力關系主要是通過微積分形式來表示扭矩，進而確定最大應力。變形幾何關系和靜力關系推出的扭轉角公式為：

式中：θ為扭轉角；M為扭矩；G為剪切彈性模量；I為對稱中心的慣性距。

根據物理關系，得出剪應力計算公式為：

式中：τ為剪切應力；M為扭矩；W為抗彎截面系數[2]。

2 計算模型

幾何模型直徑120 mm，長度100 mm，厚度2 mm，密度7.8×103kg/m3，彈性模量為195 000 MPa。共有4個有限元模型：

1）整圈模型周向均勻網格，如圖1所示；

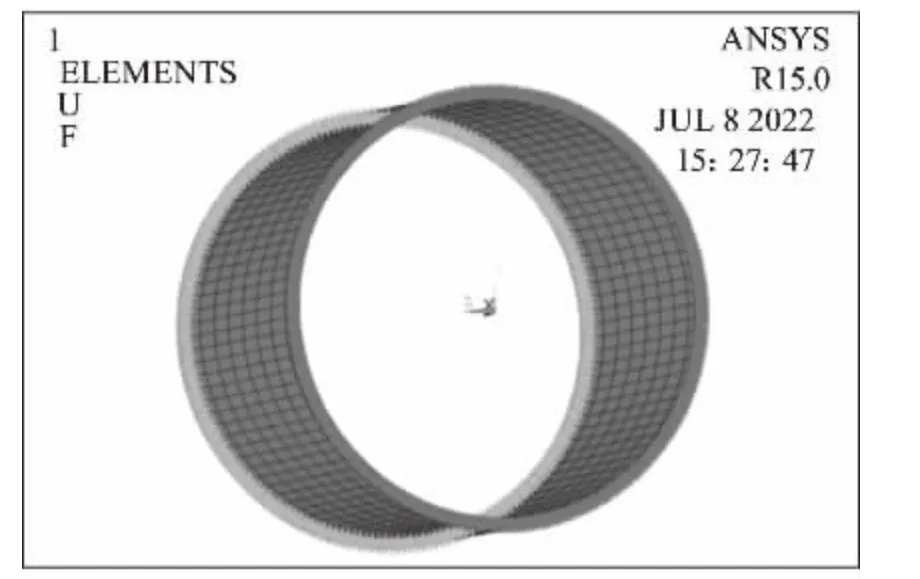
圖1 整圈模型周向均勻網格

2）整圈模型周向非均勻網格，如圖2所示；

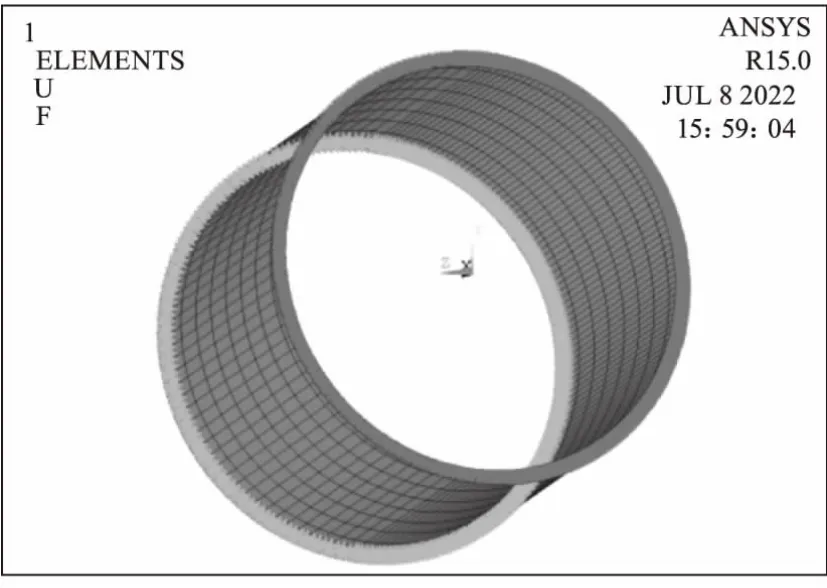
圖2 整圈模型周向非均勻網格

3）扇形段模型周向均勻網格，如圖3所示；

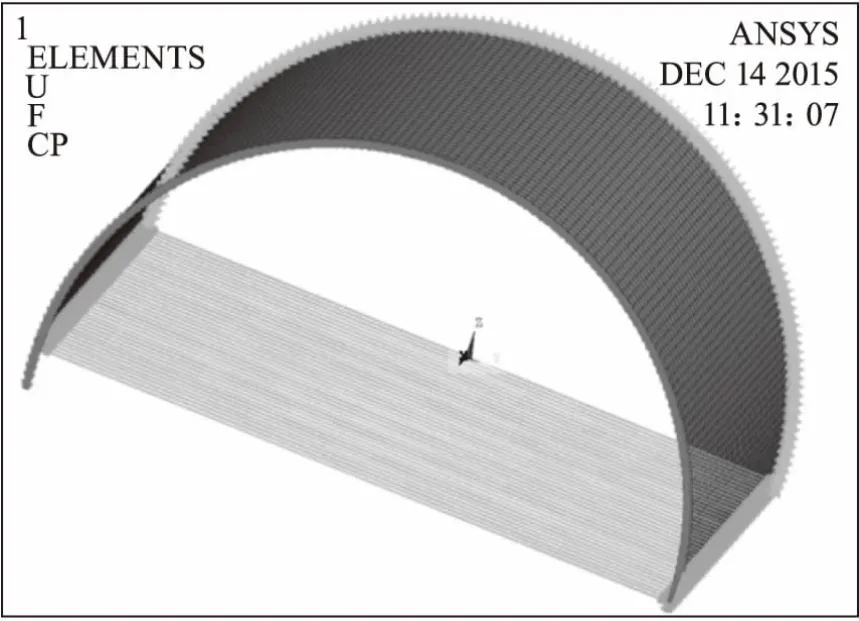
圖3 扇形段模型周向均勻網格

4）扇形段模型周向非均勻網格，如圖4所示[3-5]。

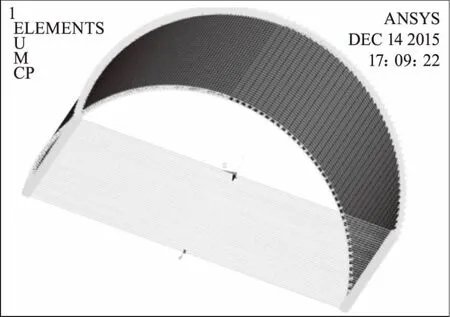
圖4 扇形段模型周向非均勻網格

3 網格及扭矩加載方式

針對第2章描述的4個有限元模型，本文嘗試了10種扭矩加載方式：

方式一：整圈模型周向均勻網格，在模型的一端進行軸向和周向約束，另一端在端點施加節點力。

方式二：整圈模型周向均勻網格，在模型的一端進行軸向和周向約束，另一端在截面中心點處施加扭矩。

方式三：整圈模型周向非均勻網格，在模型的一端進行軸向和周向約束，另一端在截面中心點處施加扭矩。

方式四：扇形段模型周向均勻網格，在模型的一端進行軸向和周向約束，另一端在端點施加節點力，在對稱面上設置循環對稱約束。

方式五：扇形段模型周向均勻網格，在模型的一端進行軸向和周向約束，另一端在截面中心點處施加扭矩，在對稱面上設置循環對稱約束。

方式六：扇形段模型周向非均勻網格，在模型的一端進行軸向和周向約束，另一端在截面中心點處施加扭矩，在對稱面上設置循環對稱約束。

方式七：整圈模型周向均勻網格，在模型的一端進行軸向和周向約束，另一端通過控制點建接觸的方法施加扭矩，相當于在實際受載荷區域建立一個剛性區域，然后把載荷施加在跟這個剛性區域連接的“pilot node”上。

方式八：整圈模型周向非均勻網格，在模型的一端進行軸向和周向約束，另一端通過控制點建接觸的方法施加扭矩，相當于在實際受載荷區域建立一個剛性區域，然后把載荷施加在跟這個剛性區域連接的“pilot node”上。

方式九：扇形段模型周向均勻網格，在模型的一端進行軸向和周向約束，另一端通過控制點建接觸的方法施加扭矩，相當于在實際受載荷區域建立一個剛性區域，然后把載荷施加在跟這個剛性區域連接的“pilot node”上。

方式十：扇形段模型周向非均勻網格，在模型的一端進行軸向和周向約束，另一端通過控制點建接觸的方法施加扭矩，相當于在實際受載荷區域建立一個剛性區域，然后把載荷施加在跟這個剛性區域連接的“pilot node”上。

方式一至方式十的有限元模型及扭矩加載方式如表1所示。

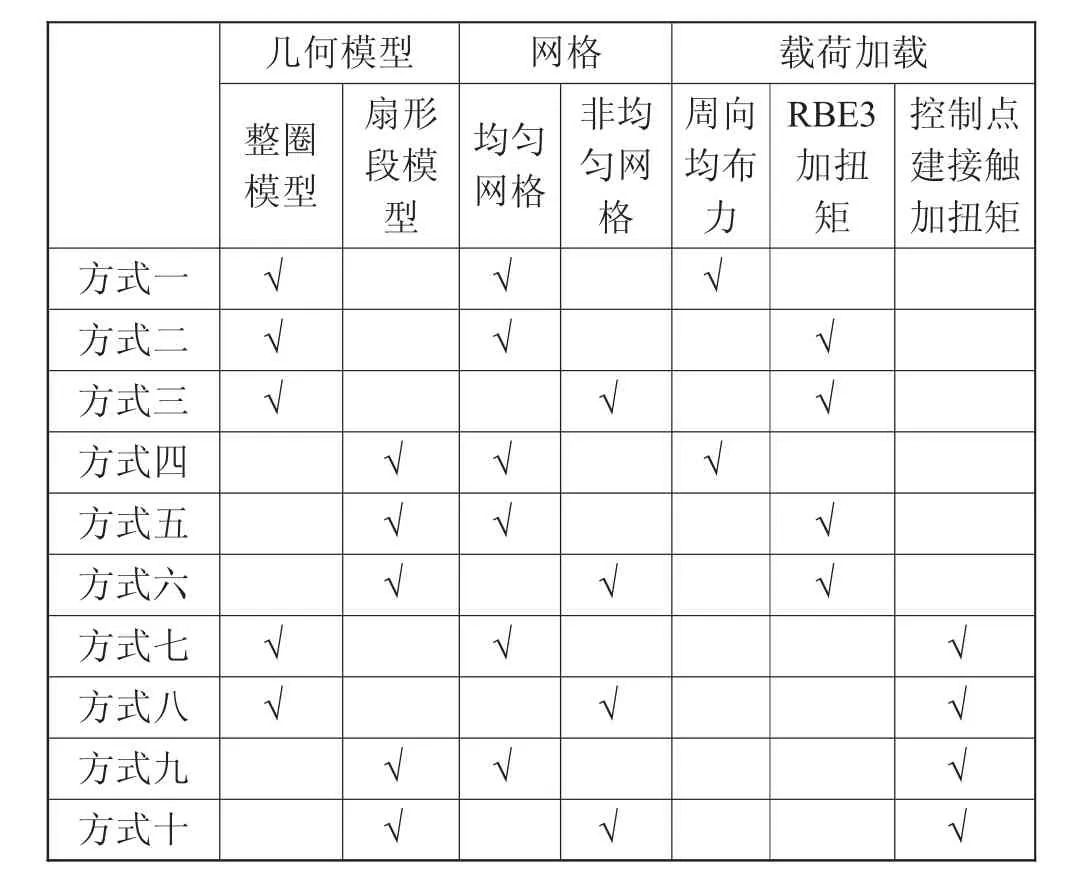
表1 有限元模型及扭矩加載方式

4 計算結果

以周向變形結果為目標，以上各種加載方式下的計算結果如圖5～14所示。

圖5 方式一周向變形

圖6 方式二周向變形

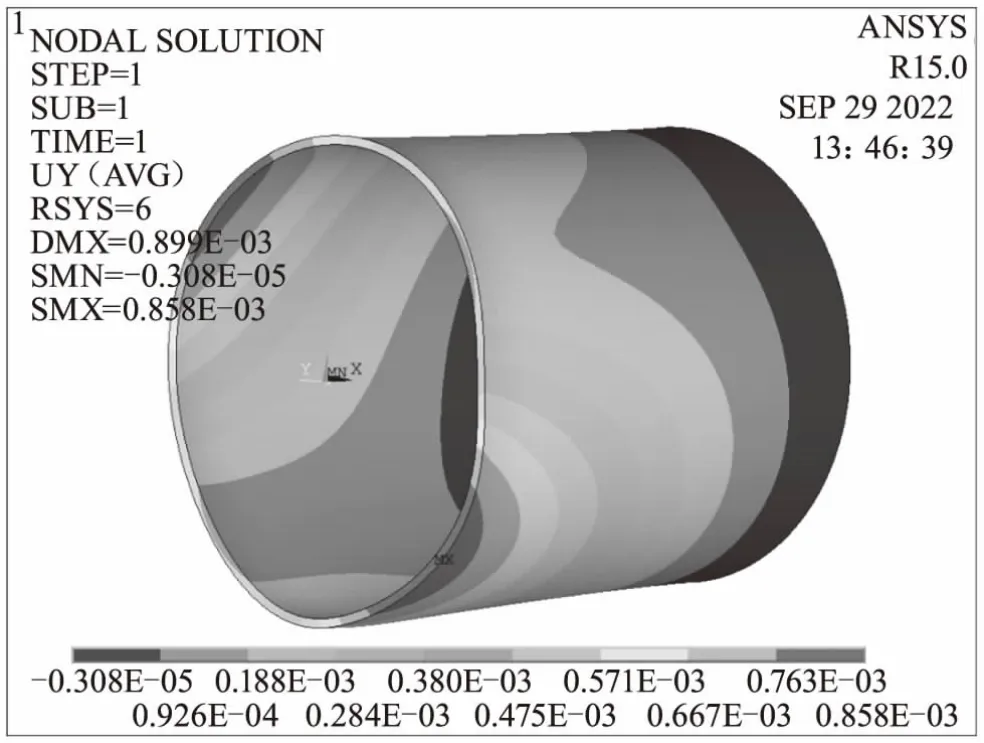
圖7 方式三周向變形

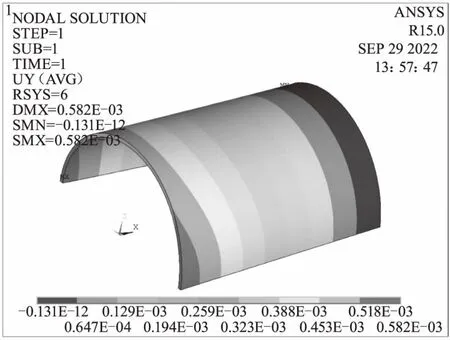
圖8 方式四周向變形

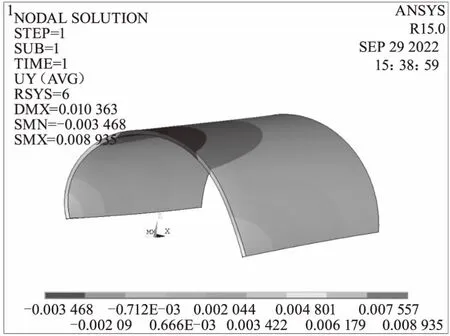
圖9 方式五周向變形

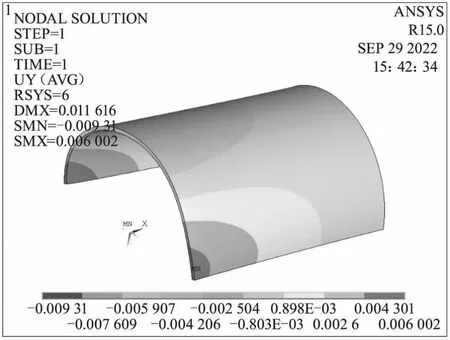
圖10 方式六周向變形

圖11 方式七周向變形

圖12 方式八周向變形

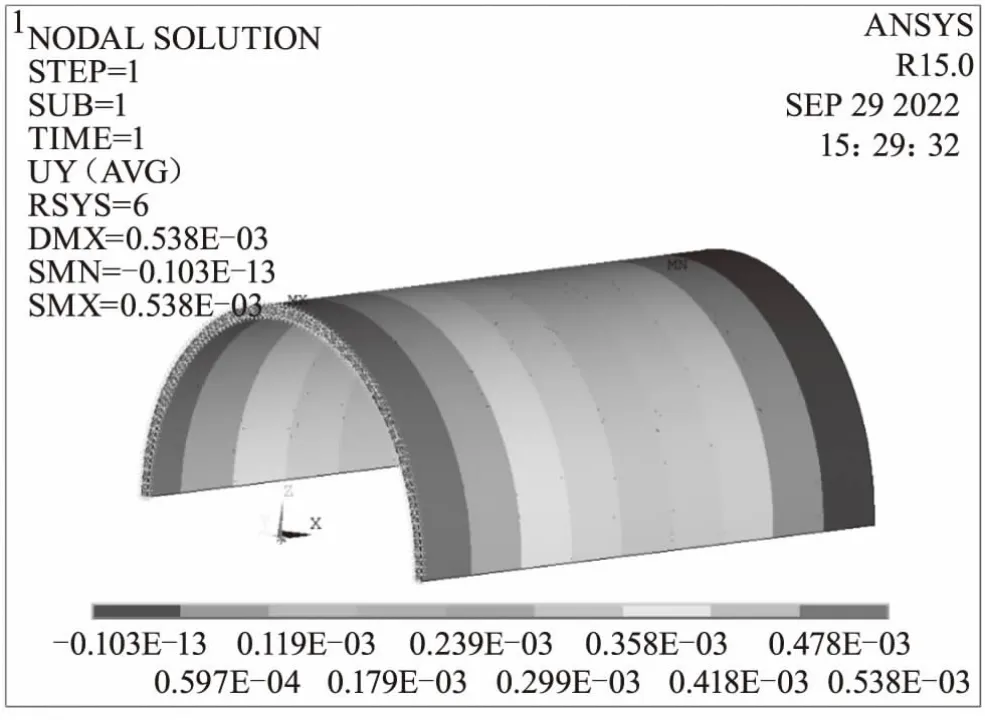
圖13 方式九周向變形

圖14 方式十周向變形

從圖5～14和表2可以看出：

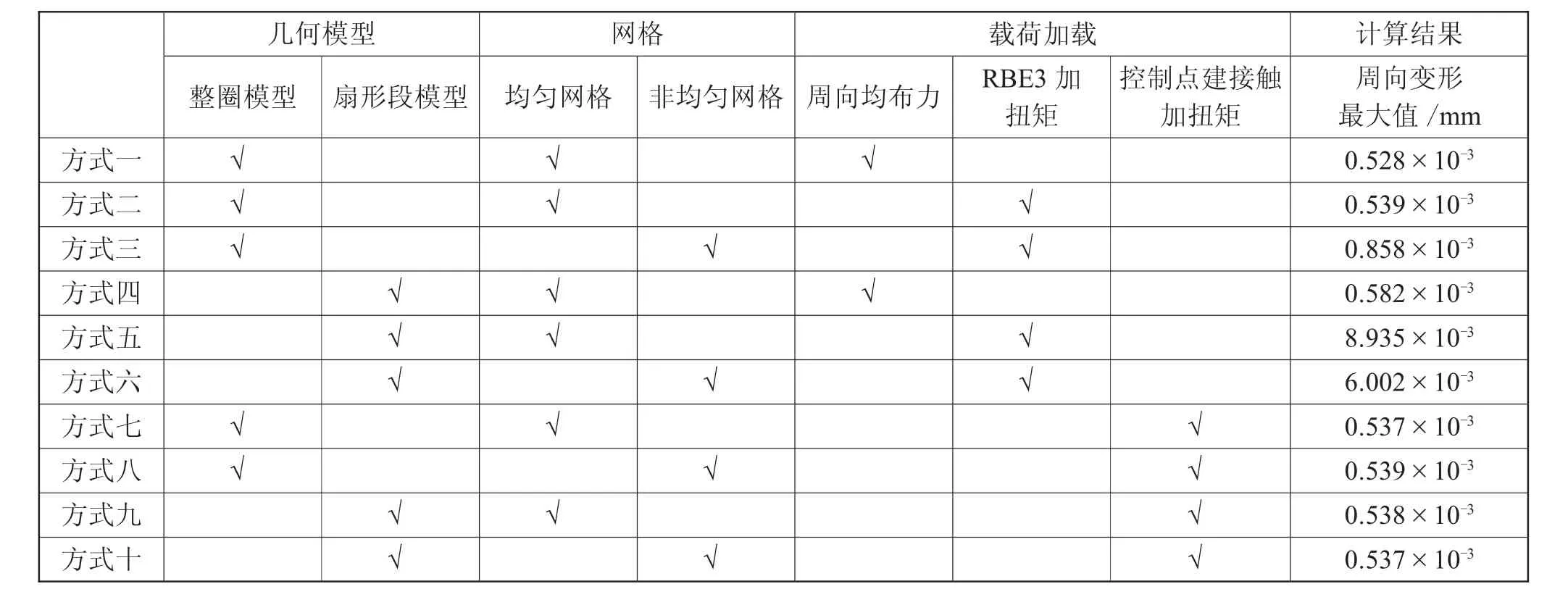
表2 有限元模型及扭矩加載方式

1）整圈模型用周向均勻網格對模型進行離散，在末端加周向力和通過RBE3在中心點加扭矩的方式得到的結果一致；

2）整圈模型用周向非均勻網格對模型進行離散，在末端通過RBE3在中心點加扭矩的方式得到的結果和整圈模型周向均勻網格得到的結果不一致；

3）扇形段模型用周向均勻網格對模型進行離散，在末端加周向力得到的結果和整圈模型周向均勻網格得到的結果一致；

4）扇形段模型用周向非均勻網格對模型進行離散，通過RBE3在中心點加扭矩，得到的計算結果和整圈模型周向均勻網格的結果不一致；

5）扇形段模型用周向非均勻網格對模型進行離散，在末端通過RBE3在中心點加扭矩得到的計算結果和整圈模型周向均勻網格的結果不一致；

6）整圈模型用周向均勻網格和周向非均勻網格對模型進行離散，通過控制點建接觸在控制點加扭矩，得到的計算結果和整圈模型周向均勻網格的結果一致；

7）扇形段模型用周向均勻網格和周向非均勻網格對模型進行離散，通過控制點建接觸在控制點加扭矩，得到的計算結果和整圈模型周向均勻網格的結果一致。

5 結論

針對各種有限元模型及扭矩加載方式，基于周向變形計算結果，得到的結論如下：

1）整圈模型均勻網格，可以用截面節點周向力、RBE3和控制點建接觸的方式施加扭矩；

2）整圈模型非均勻網格和扇形段模型（循環對稱邊界）只能用控制點建接觸的方式施加扭矩，計算結果與整圈模型均勻網格一致。

因此，結合計算效率，建議采用扇形段模型周向非均勻網格開展周向對稱零件的有限元分析。