Ni、Fe雜質在LBE中的化學行為的深度勢能分子動力學研究

梁汝婷,薄 濤,聶長明,張 蕾,柴之芳,石偉群

(1.南華大學 化學化工學院,湖南 衡陽 421001;2.中國科學院 寧波材料技術與工程研究所 先進能源材料實驗室,浙江 寧波 315201;3.中國科學院 高能物理研究所 核能放射化學實驗室,北京 100049)

當今核能領域正在大力探索第四代核電系統[1],其中鉛冷快堆[2-3]是有望第一個實現商業化的堆型。液態鉛鉍共晶(LBE,44.5%Pb-55.5%Bi)由于其良好的中子特性、熱物理性質和化學惰性[4],可用作鉛冷快堆的冷卻劑和散裂靶。LBE與傳統結構材料(如奧氏體、鐵素體和馬氏體鋼)的相容性是其在先進反應堆應用中面臨的關鍵問題之一[5-7]。LBE對鋼的腐蝕是由多種機制引起的,如金屬元素在LBE中的溶解和擴散、在界面處形成金屬間化合物以及液態金屬沿晶界滲透。在高溫和低氧濃度下,鋼的主要金屬成分Fe、Ni和Cr溶解在鋼表面,并運輸到LBE液體中,當金屬雜質濃度在LBE中達到飽和時,溶解過程停止,否則會持續腐蝕[8-10]。金屬雜質的主要運輸機制為原子向鋼表面靜止的流體層和相鄰的流動層擴散,金屬雜質的擴散速率取決于其在LBE中的濃度梯度和擴散系數。然而,目前對液態LBE中雜質原子擴散現象的認識仍然有限,在高溫下測量液態LBE中金屬雜質的擴散系數尤其困難,目前這方面的研究還很少。因此,本文擬采用理論模擬的方法研究LBE中金屬雜質擴散性質。

凝聚態系統的分子動力學(MD)模擬越來越多地應用于工程領域,它可以提供難以獲得的實驗數據和對相關物理化學性質機理的基本見解[11]。模擬方法的選擇取決于系統的特性和期望的效果。從頭算分子動力學(AIMD)[12]用于模擬液態金屬是完全可行的,該方法結合密度泛函理論(DFT)[13-14]和Car-Parrinello(CP)方法[15],從量子力學電子密度出發,對原子核上的力進行“動態”計算,可準確地描述電子與分子之間的結構、性質和相互作用。AIMD能提供重要的結構和電子信息[16](如對分布函數、態的電子密度、成鍵和電荷轉移),Gil等[17]研究了元素周期表第二排雜質原子在LBE中的微觀結構和電荷轉移;Ding等[18]研究了雜質原子在LBE中的能量關系和鍵合強度。然而,隨著原子數、模型尺寸和模擬時間的增加,計算成本呈指數增長,而擴散是一種相對緩慢的過程,需要1 ns或更長時間才能清楚地分辨出來,這限制了AIMD的應用。此外,由于系統尺寸的限制,在100個Pb和Bi原子中只允許引入1個雜質原子,在這種情況下,原子的均方根位移(決定其擴散系數)的統計數據將太過嘈雜而無法使用。使用傳統經驗勢的經典MD,在模擬體系和效率上都更具有優勢,它可以進行上萬個原子空間尺度以及ns級時間尺度的模擬,但傳統經驗勢需要獲得大量的原子間參數,耗時費力,且傳統經驗勢的適用體系范圍小,在原始參數范圍之外應用時需進行仔細測試,準確性難以保證。Zhou等[19]使用嵌入原子勢(EAM)力場研究了Pb和Bi在鋼表面的滲透深度;Gao等[20]計算了LBE的熱物理學性質,但其結果與實驗值有一定差距,得到的徑向分布函數(RDF)也達不到AIMD的精度。近年來,基于機器學習(ML)的原子間勢能得到廣泛應用,Zhang等[11-21]提出的深度勢能(DP)方法被證明是一種精確、高效的大規模長時間MD模擬方法,可以成功地解決上述精度與效率的難題。該方法從AIMD計算中選擇數據集進行訓練,通過構建深度神經網絡(DNN)[22],將原子的局部環境自動編碼為對稱保持描述符,再將描述符映射到原子勢能。經過充分訓練的DP可以達到DFT的精度。同時,DP具有傳統經驗勢的計算效率,可以計算上萬原子體系和數百納秒的時間尺度。目前深度勢能分子動力學(DPMD)已應用于眾多領域,并取得了優異的成果[23-27]。

本文擬基于DPMD方法,使用深度勢能生成軟件DP-GEN和DeePMD-Kit對液態LBE、Ni和Fe分別溶解于LBE中(LBE-Ni和LBE-Fe)的3個體系的DP模型進行訓練,并與DFT結果進行對比,以驗證DP模型的精度,最后用MD軟件LAMMPS計算3個體系的密度、熱容、黏度和雜質原子Ni、Fe在LBE中的RDF、配位數和擴散系數。

1 計算方法

1.1 深度神經網絡勢能訓練

使用DeePMD-kit軟件[28]進行DP訓練,從訓練集中的原子坐標信息(包括原子間相對徑向坐標和角坐標)出發,通過DNN構建復雜材料體系的勢能面。某一體系的勢能E由i類原子中每類原子的能量Ei的加和組成,即:

(1)

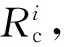
(2)

其中:Δε、ΔFi分別為DP模型預測結果與訓練數據集(DFT計算得到)之間的能量和力的差值;pε、pf和pξ分別為能量、力和維里張量的權重系數。本文在訓練過程中并未考慮維里張量,p從0.02增加到1.00,pf從1 000減少到1。LBE、LBE-Ni、LBE-Fe的DP模型分別用2 000 000、1 000 000、3 000 000步進行訓練。

1.2 主動學習生成訓練集

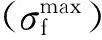
(3)

其中,〈·〉 表示模型預測的平均值。

其次，空空如也的木桶是多么沉重！因為他裝載的不只是煤炭，更是鮮活的肉身，這活著的該死的肉身實在太沉重，他既有尊嚴感卻又偏偏需要物資的侍候，想象一下騎桶者每次提著空桶前去借煤時的惶恐不安且借而不得的絕望與屈辱，他該有多么痛恨這肉身的沉重！為什么肉身就不能輕盈起來呢？——必須騎著木桶前去，如此就好像把沉重的生活騎在了胯下；必須騎著木桶前去，如此肉身就輕盈起來；輕盈的肉身，把沉重的生活騎在胯下的肉身，是活著的根本目的。——木桶必須飛起來。顯然，這是木桶飛起來的生存論依據，他超越于地球引力之上，是合乎情理的心理現實。

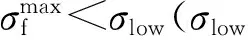
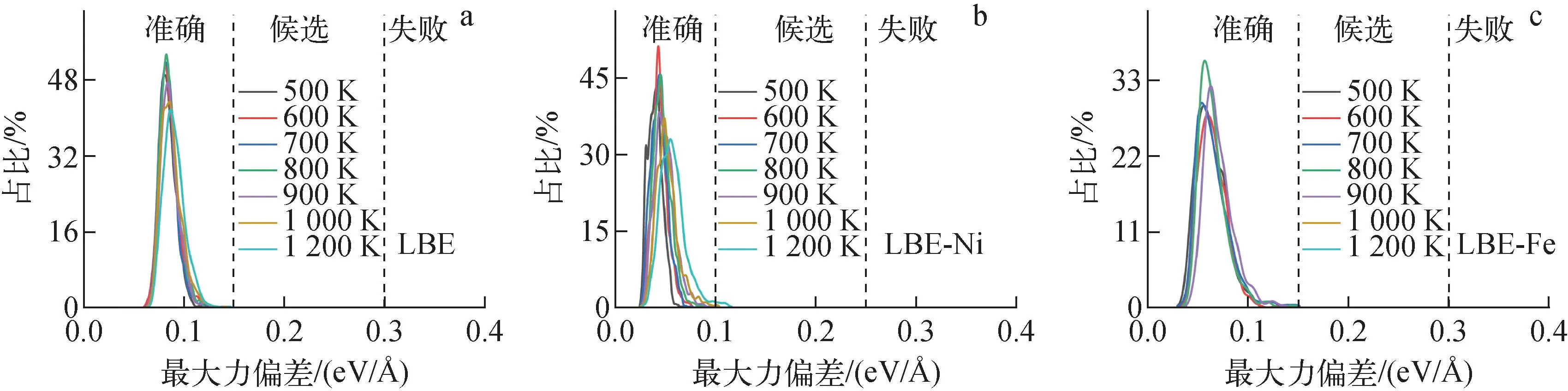
圖1 DP模型的最大力偏差Fig.1 Maximum deviation of DP model prediction of force

由圖1可見,在探索數據集的最后一步,LBE、LBE-Ni和LBE-Fe三個體系的原子最大力偏差集中在小于0.1 eV/?的范圍內,說明收集到的數據集足夠豐富,LBE、LBE-Ni和LBE-Fe體系分別包含2 000、2 900、1 500個訓練數據集。最終,使用DPGEN探索到的訓練數據集對3個體系分別進行長步數訓練。

1.3 DFT計算

DP-GEN訓練的初始訓練數據集通過AIMD模擬獲取,標記步驟中得到的候選結構需要進行DFT自洽計算。本文使用第一性原理軟件包VASP[33-34]進行所有DFT計算,用投影綴加平面波(PAW)[35-36]方法描述電子與離子的相互作用,用Perdew-Burke-Ernzerhof (PBE)[37]泛函描述電子間交換關聯作用,平面波截斷能為500 eV,K點設置為1×1×1。對于所有AIMD計算,采用NVT系綜和Nosé-Hoover恒溫器,時間步長設置為1 fs。初始結構使用Packmol程序[38]生成,對于LBE體系,初始結構由3種原子比例(Pb∶Bi=30∶70、45∶55、70∶30)和3個原子間距(2.0、2.1、2.2 ?)的9個結構通過DFT結構優化后得到,9個初始結構在700 K下模擬0.1 ps得到900個初始數據集;同時,訓練了加入范德華校正后的LBE(DFT-D3)體系和LBE(optB86b-vdW)體系的兩種DP力場,LBE(DFT-D3)體系的初始結構由3種原子比例(Pb∶Bi=30∶70、45∶55、70∶30)和3個原子間距(2.0、2.1、2.2 ?)的9個結構加入DFT-D3校正進行結構優化后得到,9個初始結構在600、800、1 000、1 200、1 400 K下模擬0.005 ps得到225個初始數據集;LBE(optB86b-vdW)體系的初始結構由3種原子比例(Pb∶Bi=30∶70、45∶55、70∶30),3個原子間距(2.0、2.1、2.2 ?)的9個結構加入optB86b-vdW校正進行結構優化后得到,初始數據集由LBE(DFT-D3)體系的驗證集加入optB86b-vdW校正后得到。對于LBE-Ni體系,初始結構由3種原子比例(Pb∶Bi∶Ni=45∶55∶1、45∶55∶3、45∶55∶5),4個原子間距(1.9、2.0、2.1、2.2 ?)的12個結構進行DFT結構優化后得到,12個初始結構分別在600、700、800、900 K下模擬0.01 ps,得到480個初始訓練數據集;對于LBE-Fe體系,初始結構由3種原子比例(Pb∶Bi∶Fe=30∶70∶5、50∶50∶5、70∶30∶5),原子間距為2.0 ?的3個結構進行DFT結構優化后得到,3個初始結構在700 K下,模擬0.1 ps,共300個初始訓練數據集。

1.4 MD模擬設置

使用MD軟件LAMMPS[39]進行DPMD模擬,所有模擬都采用周期性邊界條件來消除邊界效應。用Verlet算法求解牛頓運動方程的時間步長為1 fs。在使用DPGEN探索數據集步驟中,先在NPT系綜下迭代幾次后再用NVT系綜,可以豐富數據集,溫度范圍設為400～1 200 K,壓力范圍設為-105～2×108Pa。訓練結束后用DP模型進行DPMD模擬,模擬方法如下:各體系首先在NPT系綜下平衡60 ps,得到平衡后的結構;然后采用NPT系綜模擬0.3 ns計算熱容和密度;采用NVT系綜模擬2 ns,計算RDF、CN、擴散系數和黏度。用于DPMD模擬的初始體系由packmol建模,其中,LBE體系包含3 584個Pb原子和4 416個Bi原子;LBE-Ni體系包含2 880個Pb原子、3 520個Bi原子和64個Ni原子;LBE-Fe體系包含3 584個Pb原子、4 416個Bi原子和20個Fe原子。

2 結果討論

2.1 DP訓練和驗證

對DPGEN探索到的訓練數據集進行長步數訓練后的均方根誤差(RMSE)結果如圖2所示,可見在經過所設定步數的訓練后,RMSE均趨向于收斂,DP模型得到了充分訓練。訓練結束后,通過對驗證數據集進行測試來檢驗DP模型的準確性,驗證數據集是在DPGEN探索收斂后,由新的初始結構進行下一次DPGEN迭代生成,LBE體系的驗證數據集由若干Pb45Bi55、Pb30Bi70和Pb70Bi30組成,共300個;LBE-Ni體系的驗證集由Pb45Bi55Ni1、Pb45Bi55Ni3和Pb45Bi55Ni5組成,共241個;LBE-Fe體系的驗證集由300個Pb30Bi70Fe5、Pb45Bi55Fe5和Pb70Bi30Fe5數據組成。驗證數據集的DP與DFT計算的能量和受力的對比如圖3所示,可見3個體系的DP與DFT能量差的絕對值都小于0.01 eV/atom,力的差值在0.3 eV/?以下,說明訓練的DP力場可以準確預測體系在較寬溫度和壓強范圍的能量和原子受力。

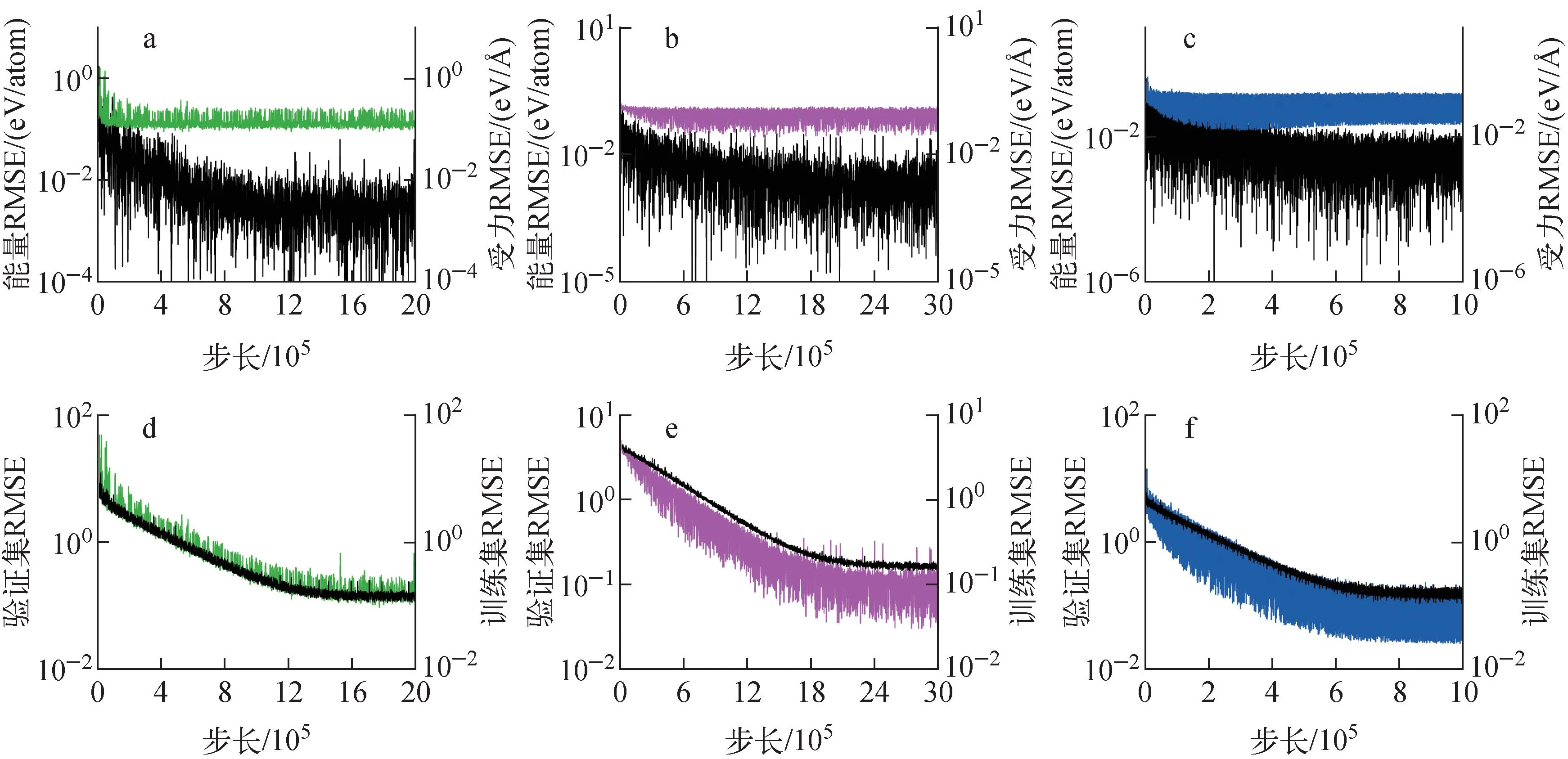
a,d——LBE體系;b,e——LBE-Ni體系;c,f——LBE-Fe體系圖2 DP模型訓練過程中訓練數據集、驗證數據集、能量和受力的均方根誤差Fig.2 Training errors in training processes of DP model

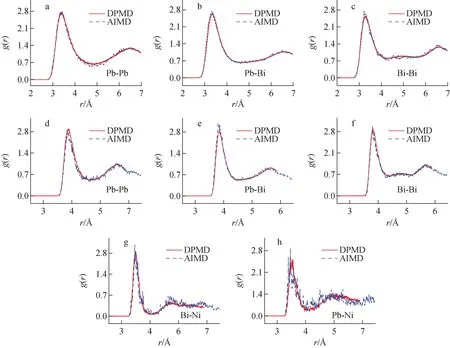
a～c——LBE體系;d～h——LBE-Ni體系圖4 773 K下DPMD與AIMD計算RDF的結果對比Fig.4 RDF results from AIMD and DPMD simulations at 773 K

為進一步驗證DP的準確性,對比了DPMD和AIMD計算3個體系RDF的結果,如圖4所示。可以看出,雖然由于AIMD模擬時LBE-Ni體系中Ni原子數量的限制,Bi-Ni和Pb-Ni的RDF較粗糙,整體上DPMD與AIMD預測的3個體系的RDF的結果吻合良好。

2.2 微觀結構

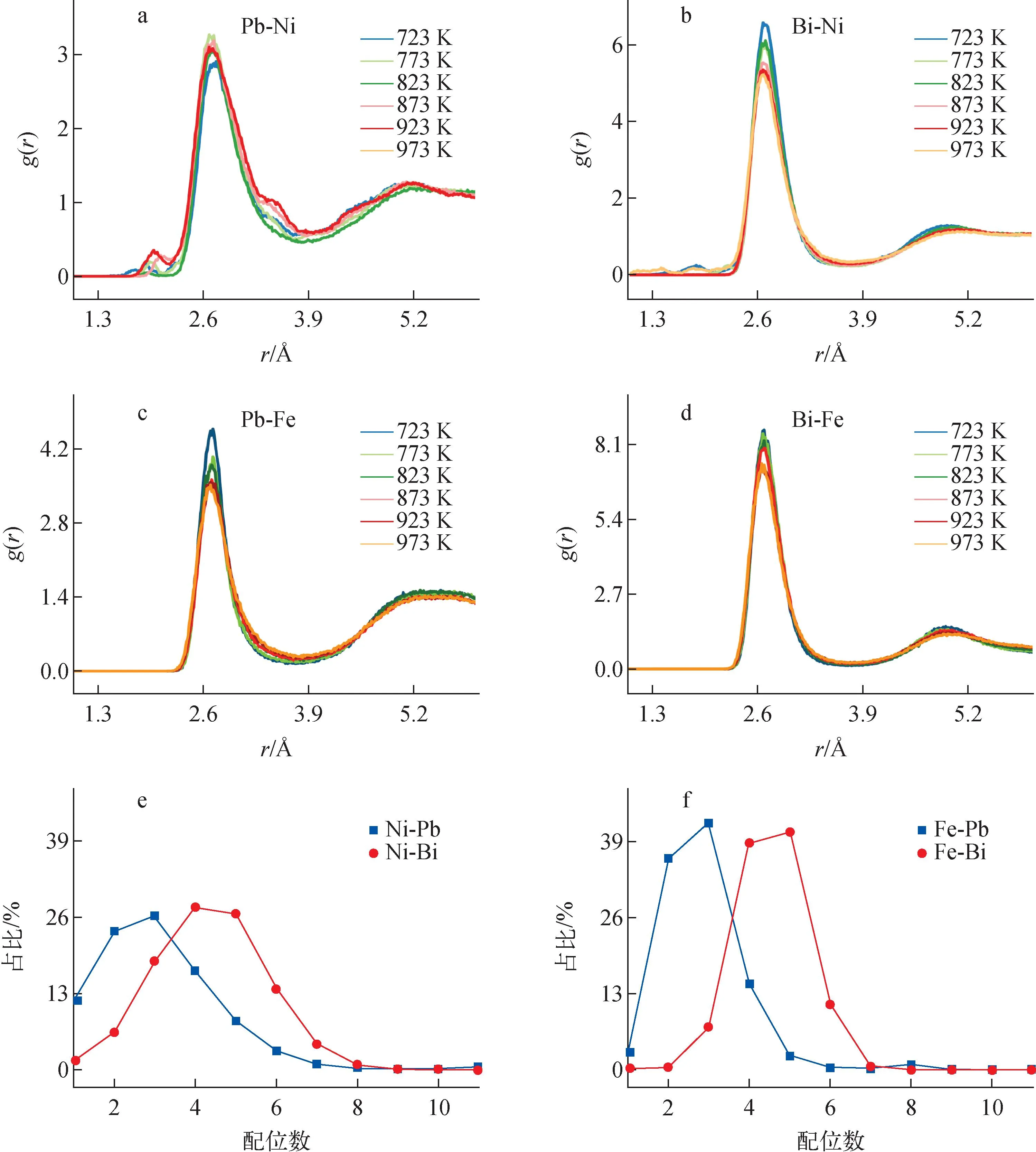
圖5 不同溫度下的RDF和773 K下Ni、Fe原子的CNFig.5 RDF results from DPMD simulations at different temperatures and coordination numbers of Ni and Fe and at 773 K

2.3 熱物理性質

1) 熱容和密度

LBE熱容的實驗數據很少[40],且差異大,在液態金屬手冊(Liquid-Metals Handbook)[41]中Lyon推薦LBE在417～673 K溫度范圍內為定值146.5 J/(kg·K),在后續的出版物[42]中Kutateladze將溫度范圍擴大至403～973 K。Hultgren等[43]則認為LBE的熱容隨溫度的升高而下降,這也與二元金屬的柯普定律相符,LBE手冊[10]根據這些數據給出了400～1 100 K內LBE比定壓熱容(cp,LBE,J/(kg·K))的擬合曲線:

cp(LBE)=164.8-3.94×10-2T+1.25×

10-5T2+1.25×10-5-4.65×10-5T-2

(4)

目前關于LBE熱容的計算數據有限,本文的DPMD結果可以提供參考值,采用DPMD計算熱容的公式如下:

(5)

其中,H、T、ρ、V分別為焓、溫度、密度、體積,密度和焓取NPT系綜模擬的0.3 ns內的平均值進行計算。

比定壓熱容的DPMD計算值與文獻結果的對比如圖6a所示。由圖6a可見,本文采用DPMD計算得到的LBE比定壓熱容在673～973 K溫度內,從140.19 J/(kg·K)下降到133.66 J/(kg·K),與LBE手冊推薦值的相對誤差為2.61%～3.35%,可見DPMD計算的結果非常準確。

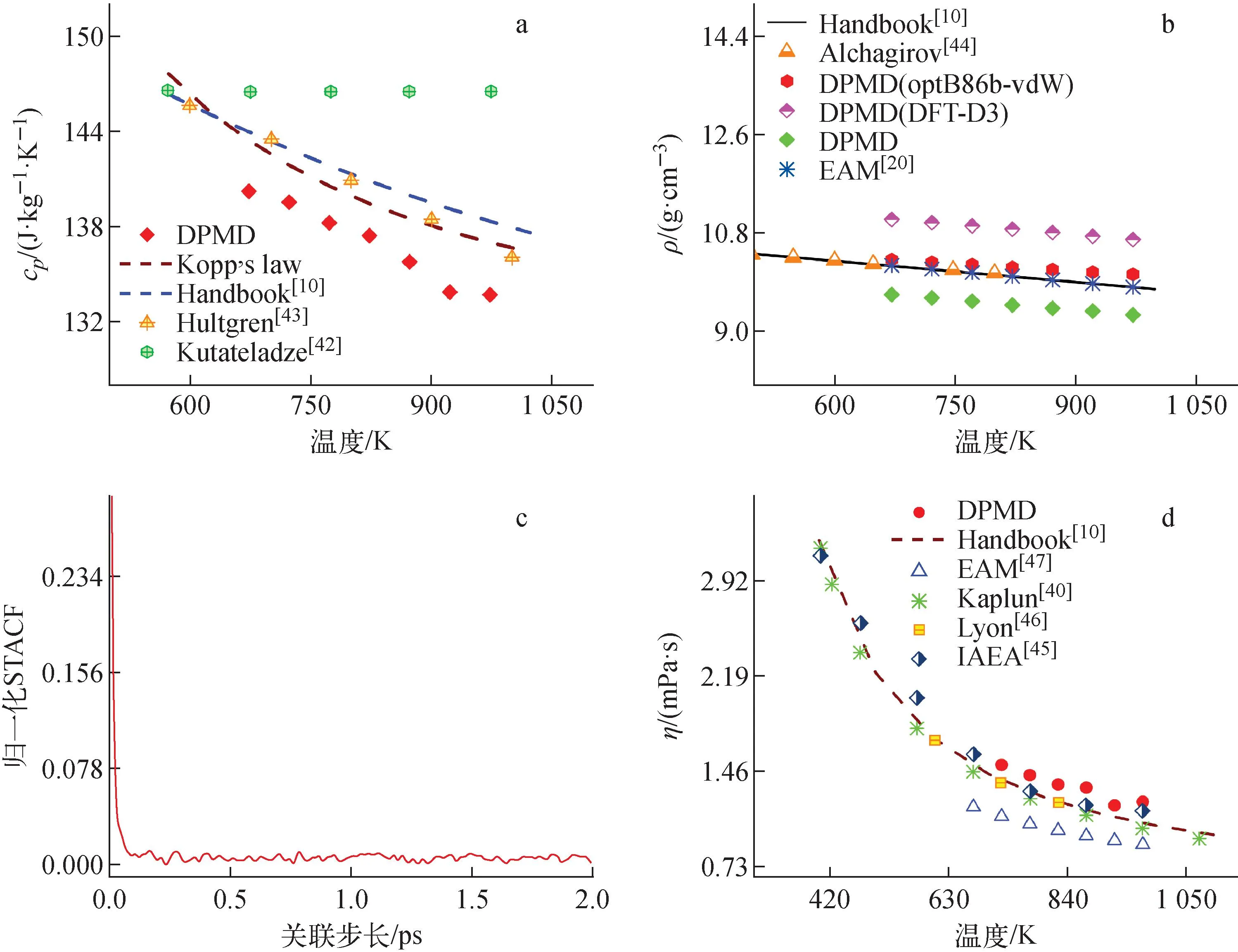
圖6 LBE熱物理性質DPMD計算值與文獻值的對比以及LBE體系應力張量自相關函數隨時間的變化Fig.6 Comparison between values of LBE thermophysical properties by DPMD and in literature and normalized stress tensor ACF at 773 K

LBE手冊對400～1 273 K內的密度推薦值為ρLBE(kg/m3)=11 065-1.293T。

本文分別用未加vdW校正(圖6b中DPMD)、加入optB86b-vdW和DFT-D3校正的3個DP力場計算了LBE的密度,并與文獻數據進行對比,結果示于圖6b。由圖6b可見,DPMD的計算結果較LBE手冊推薦值[10]略小,相對誤差在5.09%～5.18%內;而optB86b-vdW校正的計算結果與LBE手冊推薦值非常接近,相對誤差在1.18%～2.36%內;DFT-D3校正的計算結果較LBE手冊推薦值大,相對誤差在8.42%～8.90%內。可以看出,加入optB86b-vdW校正后能得到更準確的密度值,這是由于PBE泛函未考慮弱相互作用,原子間距離不夠緊密,體積偏大,導致密度偏低,引入合適的vdW校正可以解決這一問題。optB86b-vdW校正后計算得到的密度在673～973 K內從10.31 g/cm3下降到10.04 g/cm3,與實驗值[44]及Gao等[20]使用EAM力場的計算值符合較好。

2) 黏度

黏度是影響LBE流動和雜質原子擴散的重要因素,其計算公式為:

(6)

其中:kB為玻爾茲曼常數;Sxy為應力張量的分量。

本文使用Green-Kubo方法,通過應力張量自相關函數(ACF)與時間的積分計算LBE的黏度。在Green-Kubo方法中,計算ACF的時間應該足夠長,以確保歸一化的應力張量ACF可以衰減為0,由圖6c可看出,2 ps已經適用。基于此計算了723～973 K溫度下LBE的黏度,結果如圖6 d所示。由圖6d可見,LBE黏度隨溫度的升高而下降,與實驗值[40,45-46]趨勢一致,DPMD結果與LBE手冊擬合值的相對誤差為7.22%～14.3%,Gao等[47]用EAM力場的計算值與手冊推薦值的相對誤差為16.03%～20.41%,相比之下,DPMD的結果更貼近實驗值,這也驗證了DP模型的準確性。

3) 擴散系數

擴散系數(D)由均方根位移(MSD)隨時間的變化關系推導得出:

MSD=〈|δri(t)|2〉=

(7)

(8)

其中,δri為i類原子在時間t內的位移。

Ni、Fe原子不同溫度下的MSD曲線如圖7a、b所示,可見其MSD曲線并不平滑,這是由于雜質原子數量較少,其中Ni原子在LBE中的擴散速度較Fe原子更快。根據式(9)計算了Ni、Fe原子的擴散系數,結果如圖7c、d所示。實驗上關于雜質原子的擴散系數數據有限,Gao等[48]采用毛細管法測定了Ni原子在823、873、923 K LBE中擴散3.5 h和7 h的擴散系數,但由于溶解過程中Ni粉末與液態LBE邊界層Ni、Pb和Bi固體的影響,其結果與Stoke-Einstein方程所得結果有所偏離,而本文的DPMD結果(圖7c)則與Stoke-Einstein方程吻合較好,且與EAM結果[47]相比,DPMD預測的準確性更好。圖7d為Fe原子的擴散系數,與EAM的預測結果相比,本文的DPMD結果更貼近手冊值。根據DPMD計算結果擬合出Ni和Fe在673～973 K下的擴散系數(D,cm2/s)公式如下:

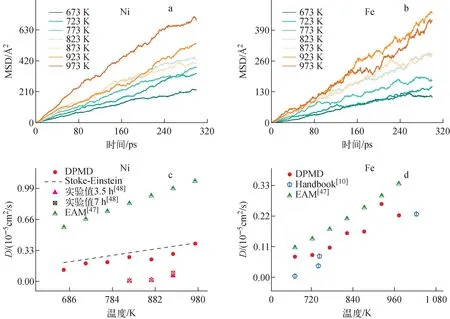
圖7 不同溫度下Ni、Fe原子在LBE中的圴方根位移與擴散系數Fig.7 MSDs and diffusion coefficient versus time for Fe atoms and Ni atoms diffusing in LBE at different temperatures

DNi=3.58×10-4exp(-1.85×104/RT)

(9)

DFe=4.65×10-4exp(-2.35×104/RT)

(10)

3 結論

本文首先訓練了LEB、LBE-Ni和LBE-Fe的DP模型,然后用它們預測了微觀結構和熱物理性質。結果表明,本文訓練的3個DP模型能準確描述LEB、LBE-Ni和LBE-Fe體系的能量和受力。3個DP模型計算得到的LEB、LBE-Ni和LBE-Fe體系的能量和受力與DFT計算結果對比,誤差分別在0.01 eV/atom和0.3 eV/?以下。3個DP模型用于計算RDF能重復AIMD的結果。不同溫度下RDF的計算結果顯示,溫度升高,原子間的作用力減小,雜質原子與Bi原子均有更強的結合能力。根據RDF峰位置得到了各原子間的距離,計算了第一配位層的CN,兩種雜質原子的配位情況相同,Pb-Ni、Pb-Fe的CN都是2和3,Bi-Ni、Bi-Fe的CN都是4。DPMD計算得到的LBE熱容隨溫度升高而減小,計算值與手冊值最大相對誤差為3.35%。計算LBE密度時,加入optB86b-vdW校正后能得到更準確的結果,計算結果與實驗值的相對誤差在1.18%～2.36%內。723～973 K下,黏度在1.95～1.22 Pa·s范圍內,且隨溫度的升高而減小,略高于實驗值。由MSD結果計算得到了雜質原子的擴散系數,Ni、Fe原子的擴散系數隨溫度的升高而增大,Ni原子在LBE中的擴散速度大于Fe原子。以上結果顯示,DP模型無論預測黏度還是擴散系數都較EAM有更好的準確性。

基于上述模擬結果,采用訓練后的DP模型可以深入了解雜質原子在LBE中的微觀結構,豐富LBE的熱物理性質數據,有利于LBE在核能系統的應用。