光伏電站與弱交流電網間次同步交互作用路徑及阻尼特性分析

高本鋒 鄧鵬程 梁紀峰 趙宇皓

光伏電站與弱交流電網間次同步交互作用路徑及阻尼特性分析

高本鋒1鄧鵬程1梁紀峰2趙宇皓2

（1. 華北電力大學河北省分布式儲能與微網重點實驗室 保定 071003 2. 國網河北省電力有限公司電力科學研究院 石家莊 050021）

大規模光伏發電經長距離輸電線路并入主網時，光伏電站和弱交流電網的交互作用可能使光伏并網系統面臨次同步振蕩（SSO）的威脅，但目前針對系統內部次同步交互作用的相關研究較少。針對上述問題，該文首先將阻尼轉矩法推廣到鎖相環（PLL）振蕩模態，并推導了光伏并網系統的線性化閉環傳遞函數框圖。然后，基于閉環傳遞函數框圖，揭示了PLL主導的SSO模式下系統阻尼構成和光伏電站與弱交流電網間動態交互過程。最后，借鑒等效阻尼系數量化評估了次同步交互作用的阻尼特性。結果表明，光伏并入弱交流電網系統存在PLL主導的SSO風險；光伏電站與弱交流電網的次同步交互作用向光伏并網系統提供負阻尼，是系統SSO的主導因素；增加PLL比例系數、交流電網強度、光伏電站光照強度或溫度，減小PLL積分系數或光伏容量，能夠增加次同步交互作用的阻尼貢獻，提高光伏并網系統穩定性。時域仿真驗證了理論分析結果的正確性。

光伏電站 次同步振蕩 次同步交互作用 阻尼轉矩法 鎖相環

0 引言

近年來，我國光伏（Photovoltaic, PV）發電新增裝機容量不斷增加[1]，已明確到2030年，風電和太陽能發電總裝機容量將達到12億kW以上，PV發電具有廣闊的發展前景[2-4]。其中，我國西北省份太陽能發電量優勢明顯[5]，是PV基地的主力區域。然而，大規模PV電站通過遠距離輸電并入電網時，系統可能存在次同步振蕩（Subsynchronous Oscilla- tion, SSO）風險，嚴重威脅新能源并網系統的穩定運行。

2015年，我國新疆哈密直驅風電場發生多起SSO事故[6]，風電場和弱交流電網間次同步交互作用是造成風機并網系統SSO的主要原因之一[7-10]。PV與風機的逆變器控制策略較為相似，并網接口具有較高的一致性，兩者表現出相似的涉網特性[11]。因此，PV電站與弱交流電網間次同步交互作用同樣存在引起PV并網系統SSO的風險。然而，鮮有文獻針對PV并網系統中次同步交互作用的機理特性展開研究。文獻[12]研究了PV并網逆變器與串補線路的交互作用對PV經串補并網系統穩定性的影響。文獻[13]建立了PV并網系統小信號模型，分析了PV電站參數和電網強度對系統SSO模態的影響。文獻[14]指出PV電站與弱交流電網在次同步頻域交點處的相位裕度不足，PV并入弱交流電網存在SSO風險。現有研究主要對PV并網系統的SSO發生機理展開分析，但系統內部次同步交互作用的阻尼特性及影響因素尚不清楚。因此，有必要對PV電站與弱交流電網間次同步交互作用展開相關分析，彌補當前PV并網系統SSO研究的不足。

目前，主流的SSO交互作用的分析方法主要有特征值法、開環模態諧振分析法和阻抗分析法。特征值法能夠分析得到系統不同SSO模態的參與變量和相關子系統[13, 15]；開環模式諧振分析法則能夠從開環模態耦合的角度揭示子系統之間的動態交互作用[16-17]。然而，基于狀態空間模型的特征值法和開環模態諧振分析法作為一種數學分析方法，分析過程物理意義不明確。基于頻域的阻抗分析法則能夠從阻抗外特性角度解釋子系統間交互作用機 理[18-19]，但其缺乏交互作用阻尼特性的量化評估指標。鑒于現有方法的局限性，亟須從新的角度對PV電站與弱交流電網間次同步交互作用進行研究。

相比于特征值法和阻抗分析法等方法，阻尼轉矩法（Damping Torque Analysis, DTA）能夠通過阻尼系數定量評估子系統間交互作用對同步機軸系穩定性的影響[20]。已有文獻通過將風機換流站的直流電容動態過程建模為類似于DTA中的同步機轉子運動方程，分析了風力發電系統直流電容振蕩模態的穩定性[21-23]。然而，DTA在PV并網系統SSO模態的穩定性分析的適用性尚不清楚。并且，當研究機網間交互作用的阻尼特性時，新能源并網系統更關注鎖相環（Phase-Locked Loop, PLL）動態特性造成的失穩[24-26]。

因此，針對PV并入弱交流電網系統中PLL主導的弱阻尼SSO模式（下文簡稱SSO模式），本文將DTA推廣到PLL動態方程，分析SSO模式下PV電站與弱交流電網間次同步交互作用的機理特性。為了便于分析，本文推導了PV并網系統閉環傳遞函數框圖，并將反映系統SSO模式阻尼的閉環擾動傳遞路徑定義為阻尼路徑。通過分析系統SSO模式阻尼路徑，揭示子系統間耦合關系和交互作用路徑，以及交互作用路徑影響系統SSO模式阻尼的動態過程。然后，通過傳遞函數推導，分離得到反映次同步交互作用的阻尼路徑，并借鑒等效阻尼系數[20]量化評估次同步交互作用的SSO模式阻尼。因此，本文方法實現了次同步交互作用阻尼特性的定量分析，有利于新能源并網系統的局部阻尼精準調控，提高系統穩定性。

本文首先將DTA推廣到PLL動態方程，實現了DTA在PV并網系統SSO模式的擴展和穩定性分析。其次，基于PV并網系統線性化閉環傳遞函數框圖，從內部擾動傳遞角度揭示了PV電站與弱交流電網間的耦合關系和交互作用路徑，并分析了交互作用路徑影響SSO模式阻尼的動態過程。然后，通過阻尼路徑分離實現次同步交互作用阻尼貢獻的量化評估。最后，分析了PLL控制參數、PV容量、交流電網強度、PV電站光照強度和溫度對次同步交互作用阻尼特性的影響。

1 PV并入弱交流電網系統

PV并入弱交流電網系統結構如圖1所示。圖1中參數及相關變量定義如下：dc為PV電站直流電容，f、f1、f2分別為濾波器電容、電感，1、2、1、2、1分別為線路電阻、電感、電容，s、s分別為電網等值阻抗；pv、dc、in、e分別為PV陣列輸出電流、直流電容電壓、PV陣列輸出功率和網側換流器輸入功率，t(t)、lcl(lcl)、g(g)分別為網側換流器端電壓（電流）、LCL濾波器電容電壓（電流）和網側電壓（電流），l、r分別為輸電線路電流和電網電壓。為便于研究PV電站與弱交流電網間次同步交互作用，本文將研究系統分為PV電站和弱交流電網兩個子系統。

圖1 PV并入弱交流電網系統結構

PV電站子系統中，PV陣列經網側換流器和濾波器輸出電能，通過一級升壓變壓器并入35 kV匯集線。研究表明，當新能源并網系統發生SSO時，新能源場站作為一個整體與電網進行動態交互[15]，基于新能源場站聚合模型得到的交互作用分析結果，對實際工程仍具有重要的參考價值[27-28]。故本文采用聚合等值模型來分析PV電站整體與弱交流電網間次同步交互作用。PV電站由150個1.4 MW的PV陣列聚合而成，光照強度和溫度均采用標準工況下參數；網側換流器基于電網電壓定向的矢量控制，采用外環定直流電壓、內環定電流的雙閉環解耦控制策略；此外，PV電站采用LCL濾波器以抑制高頻諧波，降低注入電網的諧波電流分量。PV電站具體參數見附表1。

弱交流電網子系統包含輸電線路和受端交流系統兩部分，其等效阻抗由35 kV線路阻抗1、二級升壓變壓器T、345 kV線路阻抗2及交流系統阻抗s組成，弱交流電網具體參數見附表2。交流電網強度由PV并網系統短路比（Short Circuit Ratio, SCR）確定，即

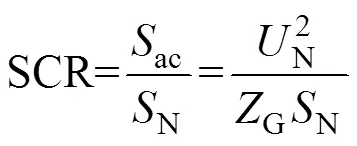
式中，ac和N分別為交流系統短路容量和PV電站額定功率；N為系統額定電壓；G為弱交流電網等效阻抗，G=1+2+T+s。

當PV電站遠距離并網時，線路阻抗增大，G增大，SCR變小，電網強度降低。通過計算可得，本文所研究的PV并網系統SCR在2～3之間（SCR= 2.5），屬于弱交流電網范疇。

2 基于DTA的PLL振蕩模態分析

本節將DTA中同步機轉子方程推廣到PLL動態方程，分析PV并網系統PLL振蕩模態的穩定性，并結合阻尼轉矩的物理意義，分析PV電站與弱交流電網間次同步交互作用的機理特性。

DTA中經典同步機轉子的線性化動態方程為

式中，為慣性時間常數；s和分別為同步系數和阻尼系數；Dd為功角增量；Dw為角速度增量；n為同步角速度；Dm和De分別為機械轉矩增量和電磁轉矩增量。當轉速產生偏差時，阻尼系數的作用為形成阻尼轉矩[29]，抑制同步機軸系振蕩，同步系數s則主要反映振蕩頻率。

下文通過傳遞函數推導將PLL的動態過程表示為類似于式（2）的形式，實現DTA在PV并網系統PLL振蕩模態的應用和穩定性分析。其中，本文線性化傳遞函數方程中變量與圖1中變量意義相同，D表示增量，下標d、q和、表示變量在相應坐標系下的對應分量，下標0表示穩態值。

圖2給出了PV電站PLL的結構原理框圖，PLL的線性化方程可表示為

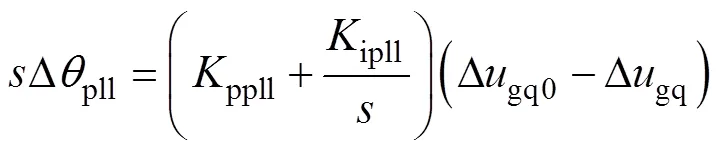
式中，Dgq為網側電壓q軸分量的增量；Dqpll為PLL輸出角的增量。

圖2 PLL結構原理框圖

令Dgq=(ppll+ipll)Dgq，式（3）可簡寫為

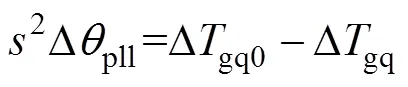
在PV并網系統中，當PLL的變量滿足Dgq=pll()Dqpll，得到Dgq的表達式為

式中，xpll()=pll()(ppll+ipll)。將算子=j代入xpll()，得到xpll()的頻域響應xpll(j)。并且，xpll(j)能夠表示為實部和虛部的組合，即

將式（6）代入式（5），得到Dgq的頻域表達式為

聯立式（4）和式（7），得到了類似于式（2）的動態方程，即

式中，e和r分別為SSO模式下相應的阻尼系數和同步系數。

因此，系統PLL動態具有類似于同步機轉子的小干擾穩定性，如圖3所示。參考DTA中相應系數的概念，SSO模式阻尼系數e和同步系數r的頻域表達式分別為Im[xpll(j)]/和Re[xpll(j)]。當Dgq0=Dgq0=0時，式（8）可表示成一個二階微分方程，其特征值為

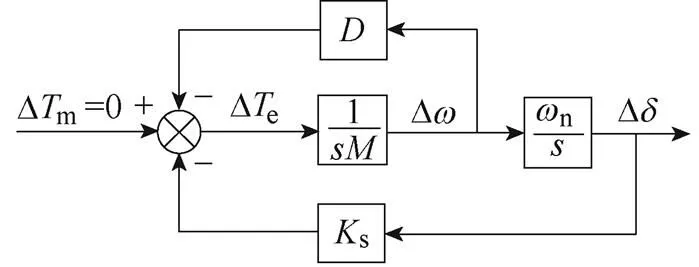
（a）同步機轉子動態方程框圖

（b）PLL動態方程框圖

圖3 DTA動態方程的應用

Fig.3 Application of DTA dynamic equation

根據DTA中阻尼系數穩定判據，e可作為SSO模式阻尼的評估指標[23]，判斷系統穩定性。由式（9）特征值得到，當e＜0時，電力系統或研究對象表現出負阻尼特性，可能導致系統SSO模式失穩。e越小，系統穩定性越差。

由e的表達式可得，SSO模式阻尼受PLL控制參數和pll()的影響。對應于本文PV并網系統，pll()刻畫了PV電站與弱交流電網的復頻域特性。通過分析pll()具體擾動傳遞過程，能夠揭示系統阻尼構成和次同步交互作用機理。本文將反映系統SSO模式阻尼的擾動傳遞路徑定義為阻尼路徑，基于阻尼路徑分析PV并網系統PLL振蕩模態下次同步交互作用的機理特性。

系統閉環傳遞函數框圖是基于阻尼路徑進行次同步交互作用分析的基礎，下一節推導PV并入弱交流電網系統的詳細閉環傳遞函數框圖，直觀地展示系統的擾動傳遞過程和阻尼路徑。

3 系統線性化模型

基于模塊化建模[30]的方法，本節根據PV電站和弱交流電網子系統的各模塊線性化傳遞函數方程，推導了PV并入弱交流電網系統的線性化模型，并得到相應詳細的閉環傳遞函數框圖。通過對比線性化模型與基于PSCAD/EMTDC的電磁暫態模型的階躍響應，驗證線性化模型及其閉環傳遞函數框圖的有效性。

3.1 PV電站模型

PV電站的動態模型包含PV陣列、直流電容、逆變器、LCL濾波器、PLL、線路電容和變壓器。PV電站的開環傳遞函數框圖推導過程如下。

本文研究SSO模式是由PV電站PLL主導的，其線性化傳遞函數方程為

式中，pll()為PLL的開環傳遞函數，其具體表達式見附錄式（A1）。

PV陣列、直流電容和網側換流器的線性化傳遞函數方程分別如式（11）～式（13）所示。

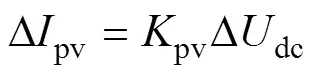
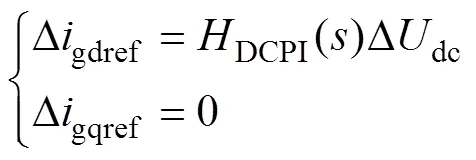
式中，pv、Pin分別為光伏陣列輸出電流和輸出有功功率的表達式；dc()、DCPI()分別為直流電容環節、直流電壓控制外環的開環傳遞函數，其具體表達式均已在附錄式（A1）中給出。

其中，網側換流器采用雙閉環解耦控制策略，并且，直流電壓控制外環的帶寬通常是電流控制內環帶寬的1/10。因此，可認為電流控制內環中網側電流的實際值能夠瞬時跟蹤其指令值[31]，即Dgd=Dgdref，Dgq=Dgqref。逆變器的功率因數通常設置為1[32]，即gqref=0，滿足Dgq=Dgqref=0。

LCL濾波器和線路并聯電容的線性化傳遞函數方程分別為

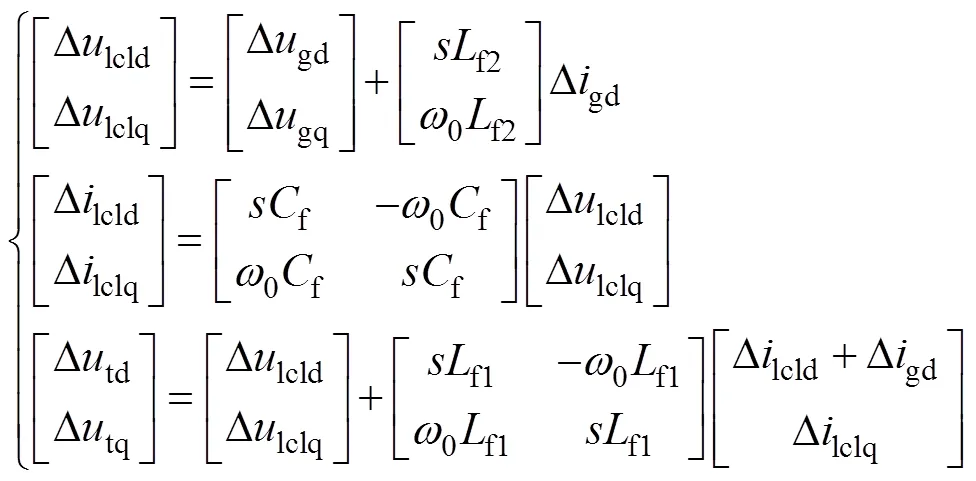
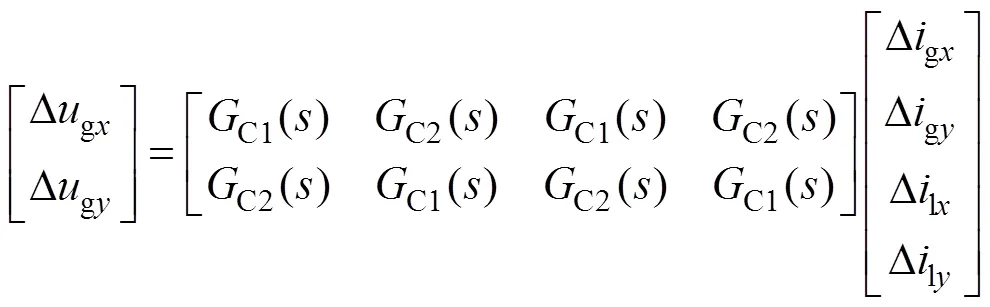
式中，C()分別為線路并聯電容在坐標系下的開環傳遞函數矩陣，其具體表達式見附錄式（A2）。并且，根據式（14），可得到LCL濾波器的開環傳遞函數框圖，如附圖1所示。

網側電壓電流在dq坐標系與坐標系間的轉換關系分別為

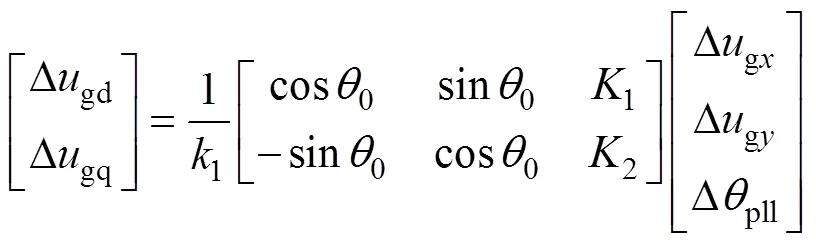
式中，為PV陣列數；1為一級升壓變壓器電壓比；1～4為坐標變換的線性化表達式，其具體表達式見附錄式（A3）。

聯立式（10）和式（16），得

式中，()為網側電壓Dg從坐標系到dq坐標系的開環傳遞函數矩陣，其具體表達式見附錄式（A4）。

聯立式（15）、式（17），消去中間變量Dg(x,y)得

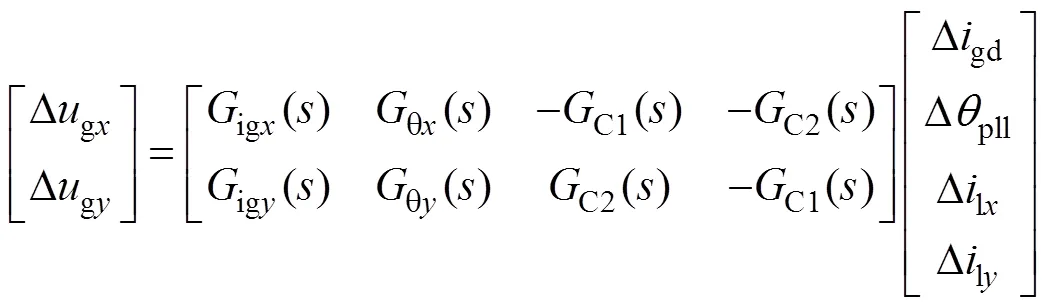
式中，C()具體表達式與式（15）一致，ig()、q()分別為網側電流Dgd、PLL輸出角Dqpll到網側電壓軸分量Dg(x,y)的開環傳遞函數矩陣，其具體表達式見附錄式（A5）。

根據式（10）、式（12）～式（14）和式（18）、式（19），得到PV電站的開環傳遞函數框圖，如圖4所示。圖4說明PV電站的線性化模型以Dl(x,y)為輸入、Dg(x,y)為輸出，框圖內擾動變量的傳遞體現了次同步擾動在PV電站中各個模塊間動態傳遞過程。

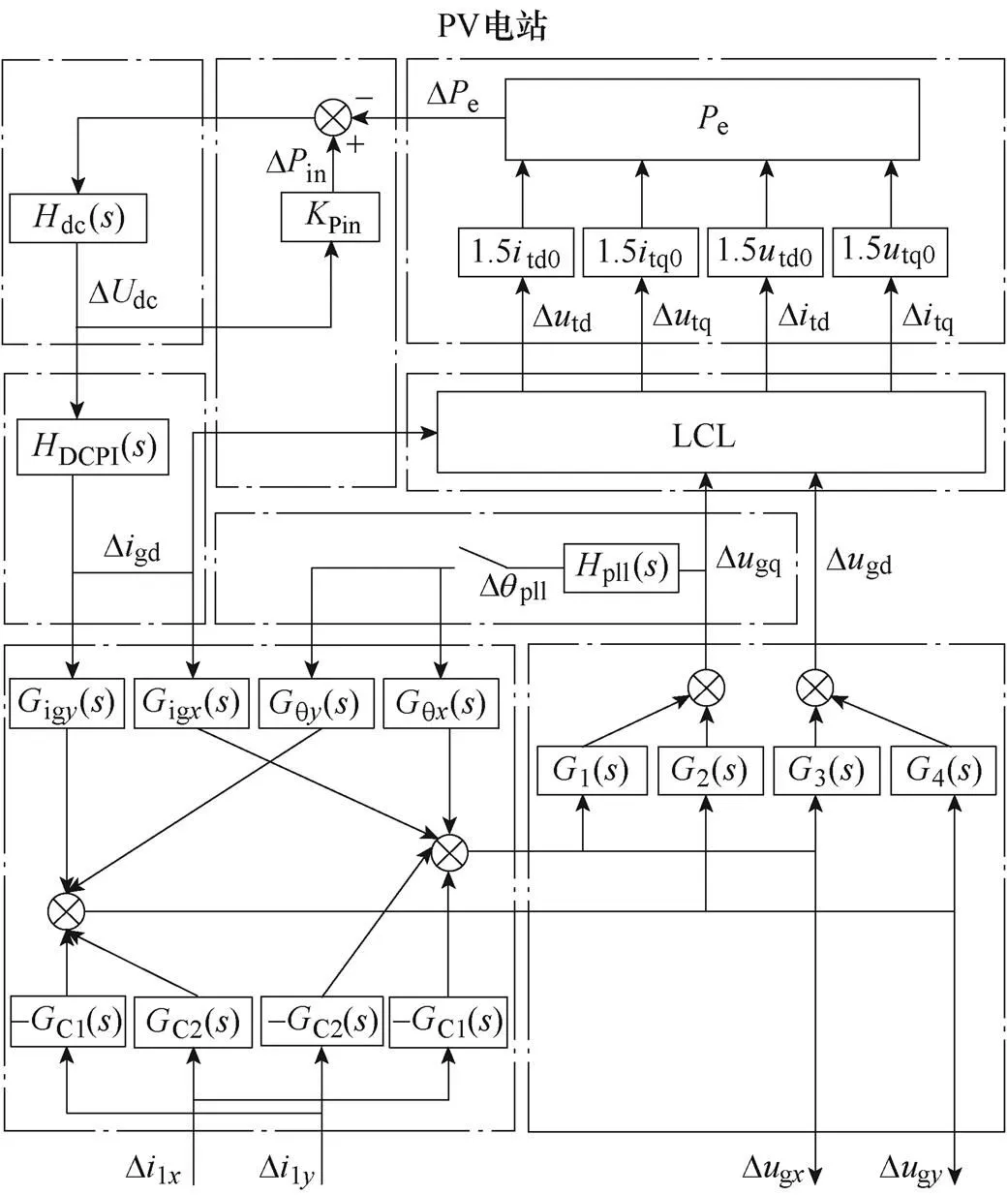
圖4 PV電站傳遞函數框圖

3.2 弱交流電網模型

弱交流電網子系統由輸電線路和受端交流系統構成，通過求取弱交流電網等效阻抗，得到其線性化傳遞函數方程為

式中，G()為弱交流電網子系統網側電壓軸分量Dg(x,y)到線路電流Dl(x,y)的開環傳遞函數矩陣，其具體表達式見附錄式（A6）。

由式（20）得到弱交流電網的開環傳遞函數框圖，如圖5所示。圖5說明弱交流電網的線性化模型以Dg(x,y)為輸入、Dl(x,y)為輸出，體現了弱交流電網導納對次同步擾動的影響。

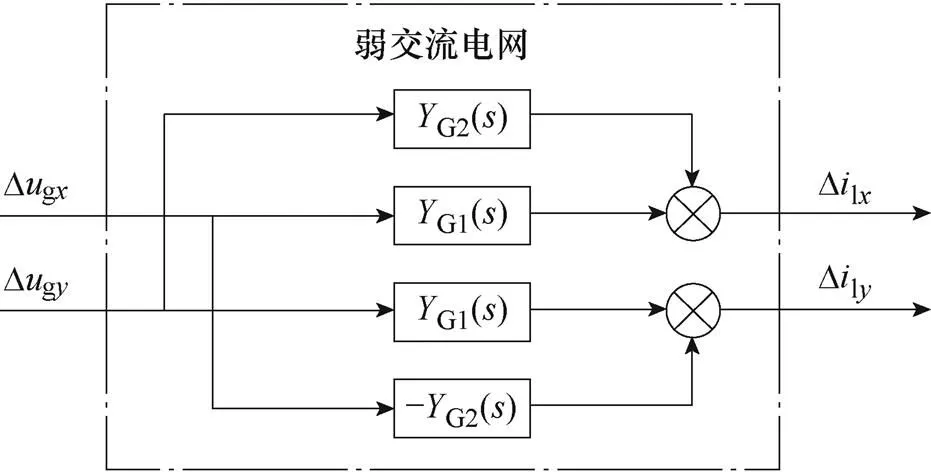
圖5 弱交流電網傳遞函數框圖

3.3 線性化模型有效性驗證

連接子系統模型的輸入輸出端口，得到PV并網系統線性化模型及其詳細閉環傳遞函數框圖，對比線性化模型與基于PSCAD/EMTDC的電磁暫態模型的階躍響應來驗證其有效性。系統參數及運行工況如第1節所述，3.0 s時PV電站直流電容電壓參考值dcref由0.965 kV階躍為1.015 kV，其他參數維持不變。圖6a～圖6d分別給出PV陣列輸出電流pv、直流電容電壓dc、網側電流d軸分量gd、網側電壓q軸分量gq在兩種模型下的階躍響應波形對比。

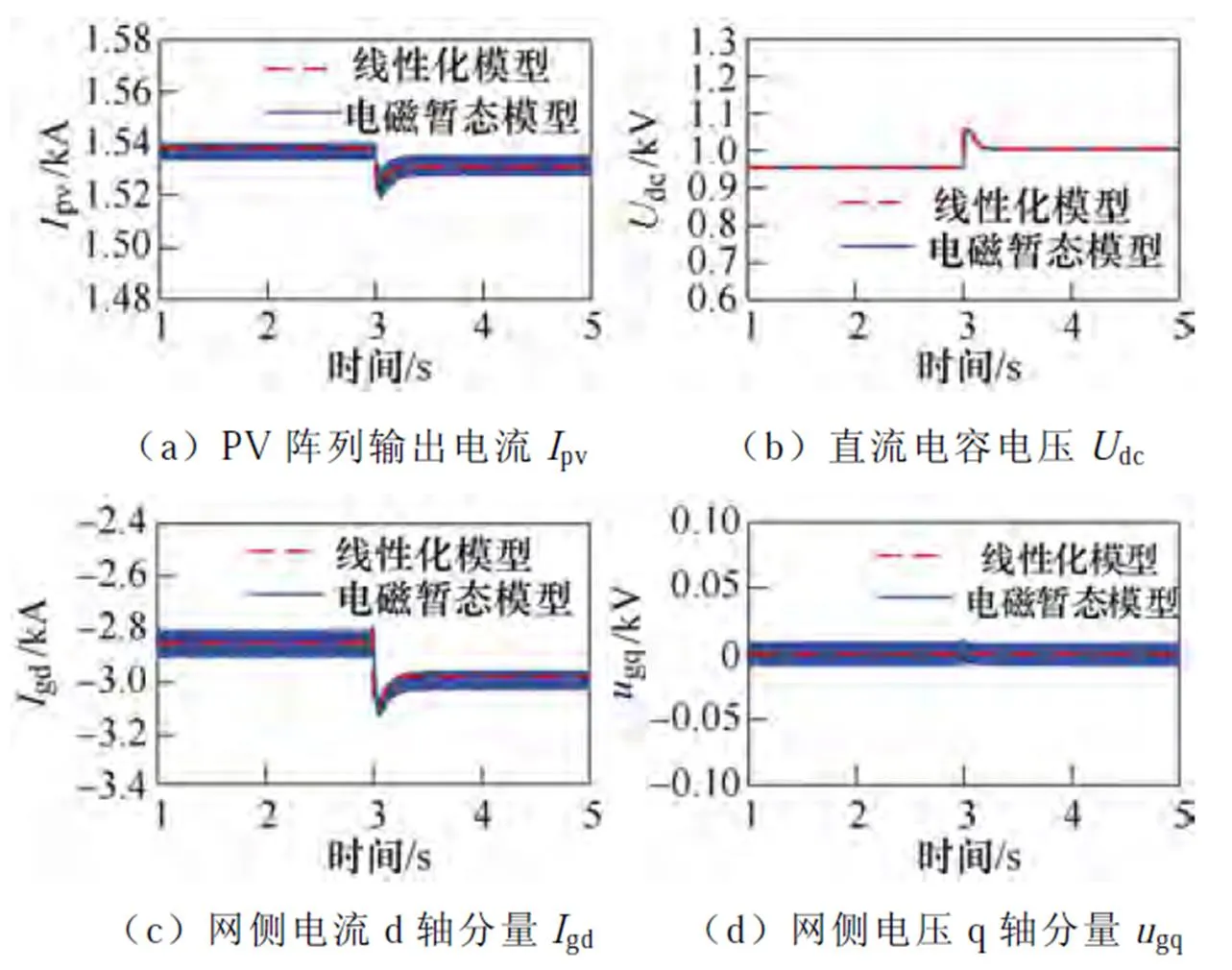
圖6 階躍響應波形

由圖6a～圖6d可得，線性化模型與電磁暫態模型的階躍響應特性基本一致，驗證了線性化模型及相應閉環傳遞函數框圖的有效性。

4 次同步交互作用路徑及阻尼特性分析

本節以PLL振蕩模態為例，基于系統閉環傳遞函數框圖，從內部擾動傳遞的角度分析PV電站與弱交流電網間次同步交互作用路徑和交互作用路徑影響SSO模式阻尼的動態過程。并且，通過等效阻尼系數量化評估系統PV并網系統中次同步交互作用的阻尼特性。

4.1 次同步交互作用路徑分析

為了直觀地反映SSO模式下PV電站與弱交流電網間動態交互過程，本節將保留PLL和并網點電壓電流變量，通過對其他環節的動態方程進行聯立、合并，簡化PV并網系統的閉環傳遞函數框圖。

由圖4可得，PV電站網側電流Dgd可表示為

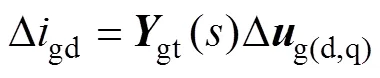
式中，gt()為PV電站從網側電壓dq軸分量Dg(d,q)到網側電流Dgd的開環傳遞函數矩陣（包含PV陣列、直流電容、逆變器以及LCL濾波器模塊）。

PV電站網側電壓軸分量Dg(x,y)可表示為

網側電壓Dg滿足坐標變換關系

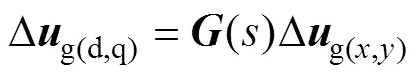
由圖5可得，弱交流電網的線性化傳遞函數方程可簡寫為

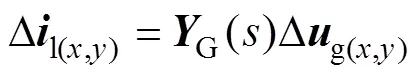
為反映PV電站與弱交流電網間變量聯系，聯立式（23）和式（24），得

式中，g()=G()-1()為弱交流電網系統網側電壓dq軸分量Dg(d,q)到線路電流Dl(x,y)的開環傳遞函數矩陣。

式（21）～式（23）表征PV電站子系統中各變量間的開環傳遞函數關系，式（25）表征弱交流電網子系統輸入量與輸出量間的開環傳遞函數關系，連接PV電站和弱交流電網的輸入輸出端口，得到PV并網系統的簡化閉環傳遞函數框圖，如圖7所示。圖7體現了擾動在PV電站各個模塊和弱交流電網導納的動態傳遞過程，箭頭表示擾動傳遞的方向。并且，在PLL主導的SSO模式下，阻尼路徑可具體表示為次同步頻率擾動圍繞PLL形成的閉環擾動傳遞路徑，如圖7中實線閉環DP。

圖7 系統閉環傳遞函數框圖

阻尼路徑DP表明SSO模式下次同步擾動從Dqpll出發，經過網側電壓Dg后返回到Dqpll。并且，阻尼路徑DP內部包含兩個閉環回路，如圖7中虛線閉環a和b。閉環a反映了PV電站各模塊對網側電壓擾動Dg的影響；閉環b反映了弱交流電網導納也將影響網側電壓擾動Dg。閉環a與閉環b之間的具體耦合關系如下：網側電壓擾動Dg通過PV電站各個模塊傳遞后導致網側電流擾動Dgd；同時，網側電壓擾動Dg通過弱交流電網導納導致線路電流擾動Dl；最后，網側電流擾動Dgd和線路電流擾動Dl在并網點再次產生網側電壓擾動Dg。綜上所述，PV電站與弱交流電網的電流擾動Dgd和Dl與網側電壓擾動Dg在并網點相互驅動，將形成次同步交互作用路徑。對于PV并入弱交流電網系統，次同步交互作用路徑循環產生的網側電壓擾動Dg與原始擾動電壓疊加，將逐步增大并網系統網側電壓波動，影響PLL輸出特性，從而導致PV電站和電網振蕩。

因此，次同步交互作用路徑與PLL形成的閉環阻尼路徑將影響SSO模式阻尼，阻尼路徑DP受到PV電站本身參數及其與弱交流電網次同步交互作用的影響。并且，已有文獻指出PV并網系統的SSO問題主要是由PV電站與弱交流電網在次同步頻域的交互作用導致的[15]，有必要針對系統內部次同步交互作用的阻尼特性展開分析。

4.2 阻尼路徑分離

為了量化分析PV并網系統中次同步交互作用的阻尼特性，本節基于系統閉環傳遞函數框圖進行阻尼路徑分離，將系統總的阻尼路徑DP分解為PV電站阻尼路徑和次同步交互作用阻尼路徑，分別定義為自阻尼路徑DP1和交互阻尼路徑DP2，并得到了單輸入單輸出（Single Input and Single Output, SISO）的系統閉環傳遞函數模型。具體步驟如下：

（1）分離自阻尼路徑DP1。將式（21）和式（23）代入式（22），消去中間變量Dgd，通過Dpll和Dl(x,y)表示網側電壓Dg(x,y)，如式（26），得到反映PV電站阻尼貢獻的自阻尼路徑DP1，如圖8a所示。

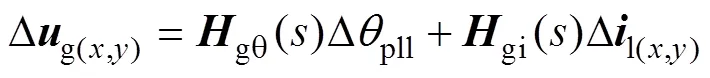
其中

（2）分離交互阻尼路徑DP2。將式（26）代入式（24），通過Dqpll表示線路電流Dl(x,y)，如式（28），實現閉環回路b與自阻尼路徑DP1的分離，得到反映次同步交互作用阻尼貢獻的交互阻尼路徑DP2，如圖8b所示。

（a）步驟1

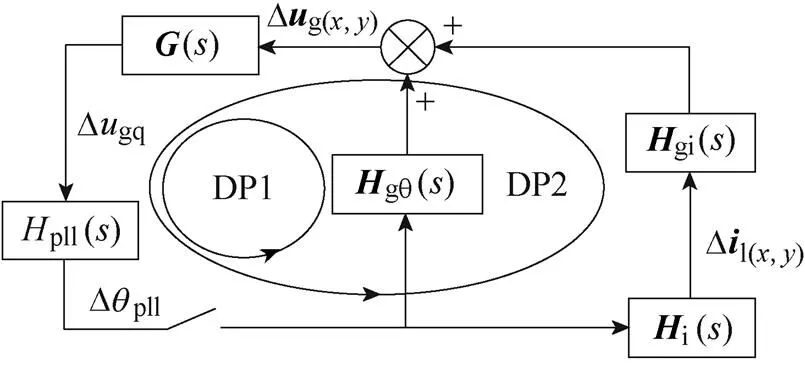
（b）步驟2

（c）步驟3

圖8 阻尼路徑分離推導

Fig.8 Derivation of damping path separation

其中

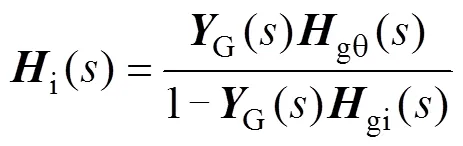
（3）求取阻尼路徑傳遞函數。消去圖8b的中間變量Dl(x,y)和Dg(x,y)，分別得到阻尼路徑DP1和DP2從Dqpll到Dgq的傳遞函數pll1()和pll2()，具體表達式見式（30），此時，系統SISO閉環傳遞函數模型如圖8c所示。

通過阻尼路徑分離，系統總的阻尼路徑DP分解為自阻尼路徑DP1和交互阻尼路徑DP2，并得到以PLL動態方程為反饋路徑的SISO閉環傳遞函數模型，為阻尼路徑的量化分析奠定基礎。

依照第2節阻尼系數定義，e=Im[xpll(j)]/，xpll()=plli()(ppll+ipll)，即可根據PLL控制參數和從?pll至?gq的傳遞函數pll()來計算阻尼路徑相應的阻尼系數。因此，根據阻尼路徑分離的結果，將pll1()和pll2()具體表達式代入阻尼系數求取公式，就能得到反映自阻尼路徑DP1和交互阻尼路徑DP2阻尼特性的阻尼系數e1和e2，即

式中，e1具體表達式僅與PV電站各模塊傳遞函數相關，表示自阻尼路徑DP1的SSO模式阻尼貢獻，稱為自阻尼系數，當e1＜0時，PV電站本身表現為負阻尼特性，PV電站并入無窮大電網會發生振蕩；e2具體表達式與PV電站和電網阻抗傳遞函數均相關，表示交互阻尼路徑DP2的SSO模式阻尼貢獻，稱為交互阻尼系數，當e2＜0時，交互作用表現為負阻尼特性，向系統提供負阻尼，降低系統穩定性。由于PV并入弱交流電網系統總的阻尼路徑由DP1和DP2構成，因此，系統總的阻尼系數e=e1+e2，當e＜0時，PV并入弱交流電網系統表現為負阻尼特性，系統會發生振蕩。

4.3 阻尼路徑貢獻評估

本節基于阻尼路徑分離結果量化分析了PV電站與弱交流電網間次同步交互作用的阻尼特性。本文將PLL的比例系數pllp和積分系數plli分別從950和1 900改為95和19 000，以激發SSO，其他參數與附錄表1和表2所示一致。基于阻尼路徑分離得到自阻尼系數e1、交互阻尼系數e2以及系統總的阻尼系數e的頻率特性曲線，如圖9所示。

由圖9可得：自阻尼系數e1在0～50 Hz均為正值，自阻尼路徑DP1向PV并網系統提供正阻尼，PV電站并入無窮大電網系統具有較高穩定性，不易振蕩。交互阻尼系數e2在11 Hz之后變為負值，交互阻尼路徑DP2向PV并入弱交流電網系統提供負阻尼，尤其13～21 Hz提供較大負阻尼，增加了系統SSO風險。系統總的阻尼系數e=e1+e2，且e在13～21 Hz的次同步頻率范圍內變為負值，說明受到PV電站與弱交流電網間次同步交互作用的影響，PV并入弱交流電網系統會發生SSO。

圖9 阻尼系數頻率特性曲線

基于PSCAD/EMTDC對上述理論分析結果進行電磁暫態仿真驗證，并通過設置受端交流系統阻抗參數，得到兩種工況。工況1：設置交流系統阻抗參數與附表2一致，模擬PV并入弱交流電網系統，對應系統總的阻尼系數e；工況2：將交流系統阻抗設置為0，模擬PV并入無窮大電網系統，對應自阻尼系數e1。在3 s時，將兩種工況下PV電站PLL的比例系數pllp和積分系數plli按照上述理論分析分別調整為95和19 000，得到PV電站網側電壓的q軸分量gq的時域仿真波形及頻譜分析結果，如圖10所示。

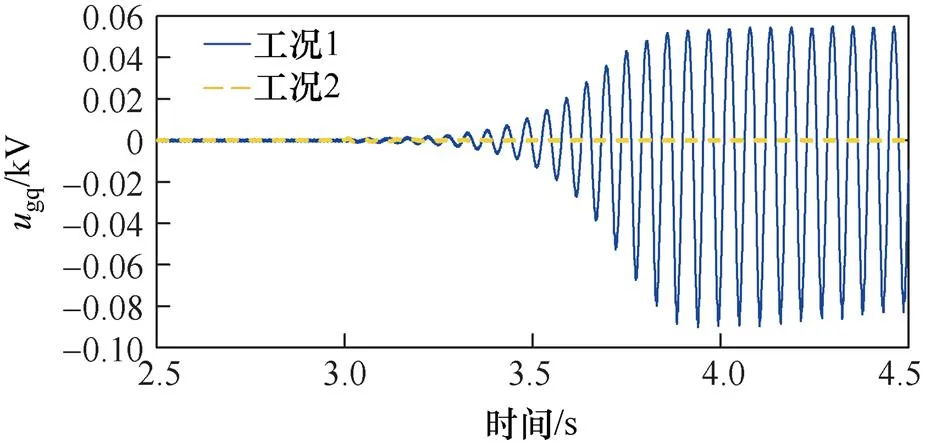
（a）網側電壓gq波形

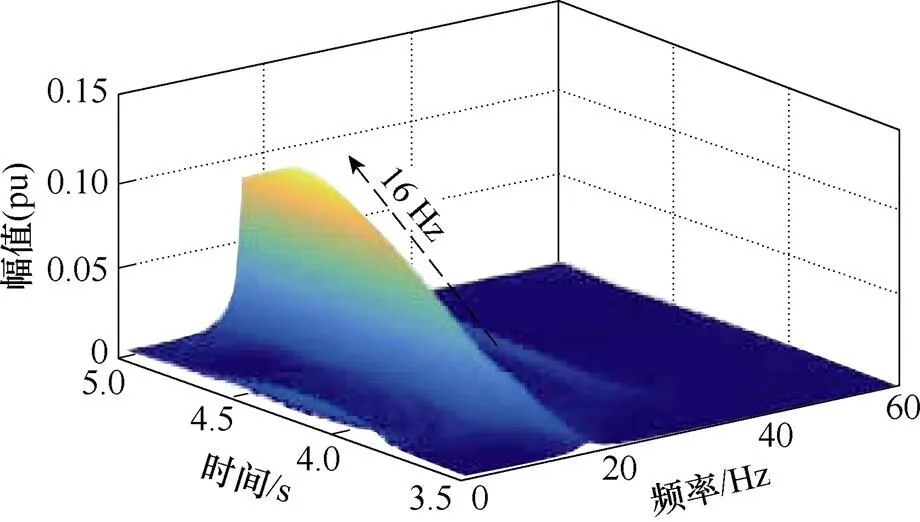
（b）FFT分析結果

圖10 網側電壓gq波形及頻譜分析結果

Fig.10 Waveforms and FFT analysis result ofgq

由圖10可得：在改變PLL的控制參數后，工況2系統能夠保持穩定，與e1在0～50 Hz大于0相符；但工況1系統發生了振蕩，且gq的振蕩頻率主要為16 Hz，與e在SSO頻域小于0相符。兩種工況下系統不同的穩定性說明在SSO模式下，PV電站與弱交流電網間次同步交互作用向系統提供負阻尼，導致PV并入弱交流電網系統呈現負阻尼特性，與e2在SSO頻域小于0的理論分析相符。

上述分析證明了阻尼路徑分離結果的有效性，并得到SSO模式下，雖然PV電站自阻尼路徑DP1向系統提供正阻尼，但由于交互阻尼路徑DP2向系統提供了負阻尼，PV并入弱交流電網系統可能會發生振蕩。值得注意的是，本文分析方法也適用于PV并網系統其他振蕩模態下次同步交互作用阻尼特性的分析。

5 阻尼特性影響因素分析

根據阻尼路徑分離結果可得，PV并入弱交流電網系統阻尼受到自阻尼路徑和交互作用路徑的影響，且交互阻尼路徑對系統穩定性影響較大。然而，現有文獻大多直接分析系統總的阻尼特性，對次同步交互作用阻尼特性的研究較少。因此，針對SSO模式下PV電站與弱交流電網間次同步交互作用的阻尼特性，本節分析了PLL控制參數、PV容量、交流電網強度、PV電站光照強度和溫度對自阻尼路徑和交互阻尼路徑阻尼貢獻的影響，并得到系統阻尼特性變化的主導路徑。

5.1 PLL控制器參數

將PV電站中PLL的ppll和ipll分別設置為95和19 000，以激發SSO。分別改變PV電站PLL控制參數，得到e、e1和e2的頻率特性曲線，如圖11所示。在圖11a中，PLL的比例系數ppll分別為76、95和114，在圖11b中，PLL的積分系數ipll分別為15 200、19 000和22 800。箭頭表示阻尼系數隨參數增加而變化的方向，后文不再贅述。

由圖11a可得：在SSO頻率附近，隨著ppll的增加，e、e1和e2均上移，但e2變化不明顯。結果表明，隨著ppll的增加，自阻尼路徑的阻尼貢獻增大，PV電站保持正阻尼特性；交互阻尼路徑的阻尼貢獻略微增大；PV并入弱交流電網系統的阻尼將增加，且自阻尼路徑阻尼貢獻增大是系統阻尼特性變化的主導因素。

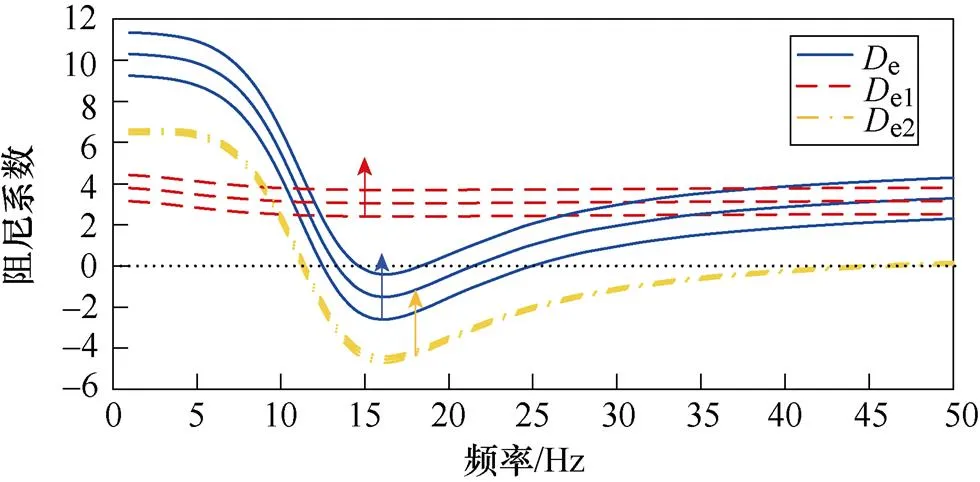
（a）比例系數

（b）積分系數

圖11 PLL控制參數的影響

Fig.11 Influence of PLL control parameters

由圖11b可得：在SSO頻率附近，隨著ipll的增加，e、e1和e2均下移，但e1變化不明顯。結果表明，隨著ipll的增加，自阻尼路徑的阻尼貢獻略微減小，PV電站保持正阻尼特性；交互阻尼路徑提供的阻尼貢獻同樣減小；PV并入弱交流電網系統的阻尼將減小，且交互阻尼路徑阻尼貢獻減小是系統阻尼特性變化的主導因素。

為驗證PLL控制參數對系統穩定性的影響，在3.0 s時分別改變PLL的控制參數，得到PV并入弱交流電網系統中gq的時域仿真波形，分別如圖12a和圖12b所示。

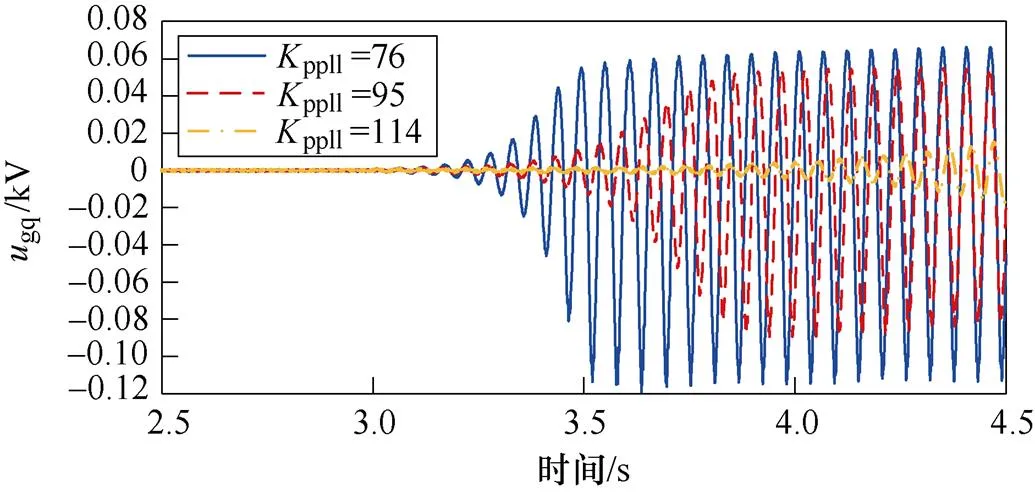
（a）比例系數

（b）積分系數

圖12gq波形（PLL控制參數變化）

Fig.12 Waveforms ofgq(PLL control parameters change)

從圖12可以看出，隨著ppll的增加，gq的振幅減小，系統SSO模式阻尼逐漸增加；隨著ipll的增加，gq的振幅增加，系統SSO模式阻尼逐漸減小。時域仿真結果與理論分析一致。

5.2 PV容量

將PV電站中PLL的ppll和ipll分別設置為95和19 000，以激發SSO。當PV容量分別為154、182和210 MW時，得到e、e1和e2的頻率特性曲線，如圖13所示。

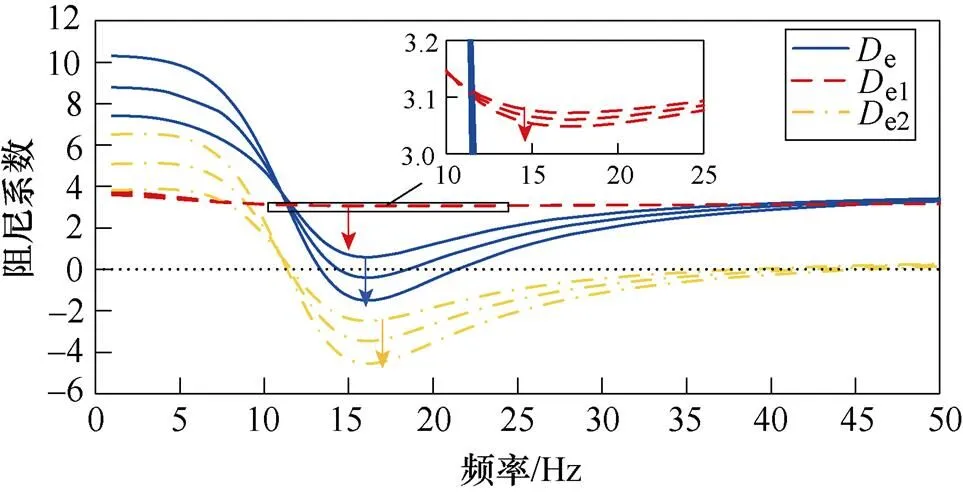
圖13 PV容量的影響

由圖13可得：在SSO頻率附近，隨著PV容量的增加，e、e1和e2均下移，但e1變化不明顯。結果表明，隨著PV容量的增加，自阻尼路徑的阻尼貢獻略微減小，PV電站保持正阻尼特性；交互阻尼路徑的阻尼貢獻減小；PV并入弱交流電網系統的阻尼將減小，且交互阻尼路徑阻尼貢獻減小是系統阻尼特性變化的主導因素。另外，當PV容量為154 MW時，系統表現為正阻尼特性。

為驗證PV容量對系統穩定性的影響，在3.0 s時改變PV容量，得到PV并入弱交流電網系統中gq的時域仿真波形，如圖14所示。

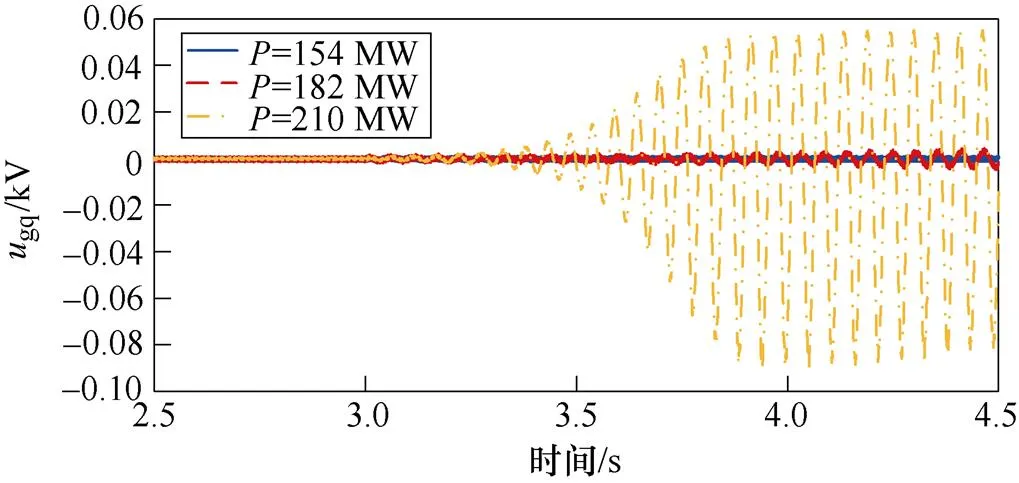
圖14 ugq波形（PV容量變化）

由圖14可得：當PV容量為154 MW時，系統不發生振蕩。隨著PV容量的增加，gq發生振蕩且振幅增大，系統SSO模式阻尼逐漸減小。時域仿真結果與理論分析一致。

5.3 交流電網強度

將PV電站中PLL的ppll和ipll分別設置為95和19 000，以激發SSO。改變弱交流電網等效阻抗，模擬PV并入弱交流電網系統時不同交流電網強度的影響。通過SCR反映交流電網強度，當SCR分別為2.0、2.5和3.0時，得到e、e1和e2的頻率特性曲線，如圖15所示。

圖15 SCR的影響

由圖15可得：在SSO頻率附近，隨著SCR的增加，e和e2上移，e1不隨SCR變化而移動。結果表明，隨著SCR的增加，僅與PV電站參數相關的自阻尼路徑阻尼貢獻不變，PV電站保持正阻尼特性；交互阻尼路徑的阻尼貢獻增大；PV并入弱交流電網系統的阻尼將增加，且交互阻尼路徑阻尼貢獻增大是系統阻尼特性變化的主導因素。

為驗證SCR對系統穩定性的影響，在3.0 s時改變SCR，得到PV并入弱交流電網系統中gq的時域仿真波形，如圖16所示。

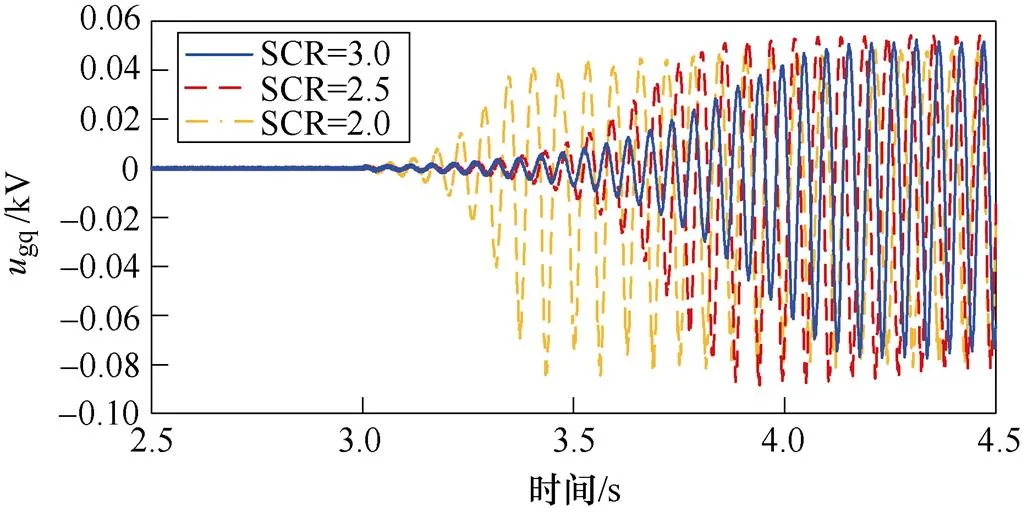
圖16 ugq波形（SCR變化）

由圖16可得：隨著交流電網強度的增強，gq的振蕩程度減弱，系統SSO模式阻尼逐漸增加，且在一定的弱交流電網強度范圍內，系統都會發生SSO。時域仿真結果與理論分析一致。

5.4 PV電站光照強度

將PV電站中PLL的ppll和ipll分別設置為95和19 000，以激發SSO。當PV電站光照強度分別為975、1 000和1 025 W/m2時，得到e、e1和e2的頻率特性曲線，如圖17所示。

圖17 光照強度的影響

由圖17可得：在SSO頻率附近，隨著光照強度的增加，e、e1和e2均上移，但e1變化不明顯。結果表明，在標準工況附近，隨著光照強度的增加，自阻尼路徑的阻尼貢獻略微增大，PV電站保持正阻尼特性；交互阻尼路徑的阻尼貢獻增大；PV并入弱交流電網系統的阻尼將增大，且交互阻尼路徑阻尼貢獻增大是系統阻尼特性變化的主導因素。

為驗證PV電站光照強度對系統穩定性的影響，在3.0 s時改變光照強度，得到PV并入弱交流電網系統中gq的時域仿真波形，如圖18所示。

圖18 ugq波形（光照強度變化）

由圖18可得：在一定范圍內，隨著PV電站光照強度的增加，gq振幅減小，系統SSO模式阻尼逐漸增大。時域仿真結果與理論分析一致。值得注意的是，當算例偏離標準工況較大，系統原本的穩定工作點同樣會發生振蕩。

5.5 PV電站溫度

將PV電站中PLL的ppll和ipll分別設置為95和19 000，以激發SSO。當PV電站溫度分別為15、20和25℃時，得到e、e1和e2的頻率特性曲線，如圖19所示。

由圖19可得：在SSO頻率附近，隨著PV電站溫度的增加，e、e1和e2均上移，但e1變化不明顯。結果表明，隨著溫度的增加，自阻尼路徑的阻尼貢獻略微增大，PV電站保持正阻尼特性；交互阻尼路徑的阻尼貢獻增大；PV并入弱交流電網系統的阻尼將增大，且交互阻尼路徑阻尼貢獻增大是系統阻尼特性變化的主導因素。

圖19 溫度的影響

為驗證PV電站溫度對系統穩定性的影響，在3.0 s時改變溫度，得到PV并入弱交流電網系統中gq的時域仿真波形，如圖20所示。

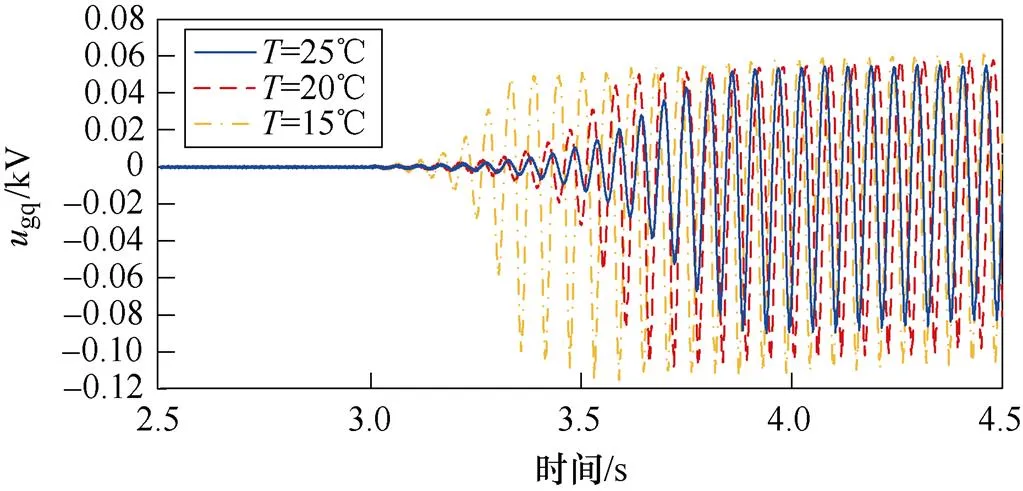
圖20 ugq波形（溫度變化）

由圖20可得：在一定范圍內，隨著PV電站溫度的增加，gq振蕩程度減小，系統SSO模式阻尼逐漸增大。時域仿真結果與理論分析一致。

上述研究結論表明：對于PV并入弱交流電網系統，PLL比例系數主要通過改變PV電站阻尼貢獻影響系統阻尼特性，PLL積分系數、PV容量、交流電網強度、PV電站光照強度和溫度則對PV電站阻尼貢獻的影響較小，主要是通過改變PV電站與弱交流電網間次同步交互作用阻尼貢獻影響系統阻尼特性。考慮到PV電站與弱交流電網間次同步交互作用是PV并入弱交流電網系統SSO的主導因素，通過優化后者參數能夠較好地保持PV電站原本的阻尼特性，提高PV并入弱交流電網系統穩定性，實現了PV并網系統阻尼的精準調控。

6 結論

本文基于阻尼轉矩法在PLL振蕩模態的擴展，分析了PV電站與弱交流電網間次同步交互作用路徑，揭示了交互作用路徑影響系統SSO模式阻尼的動態過程，并量化評估了次同步交互作用的阻尼特性。主要研究結論如下：

1）PV并入弱交流電網系統存在PLL主導的SSO風險。PV電站與弱交流電網的電流擾動和網側電壓擾動在并網點相互驅動，形成次同步交互作用路徑，且交互作用路徑將通過PLL形成阻尼路徑，影響系統SSO模式阻尼。

2）通過系統阻尼路徑分離，能夠量化評估PV電站和次同步交互作用的SSO模式阻尼貢獻。次同步交互作用向系統提供負阻尼，是PV并入弱交流電網系統SSO的主導因素。

3）在一定范圍內，PLL比例系數、交流電網強度、PV電站光照強度或溫度增大時，次同步交互作用及PV并網系統SSO模式阻尼增加；而PLL積分系數或PV容量增大時，次同步交互作用及PV并網系統SSO模式阻尼減小。

4）針對次同步交互作用的負阻尼特性合理設計系統參數，能夠有效增加PV并入弱交流電網系統SSO模式阻尼，同時較好地保持PV電站原本的阻尼特性，對實際工程具有一定的指導意義。

附 錄

1. 仿真系統參數說明

附表1 PV電站主要參數

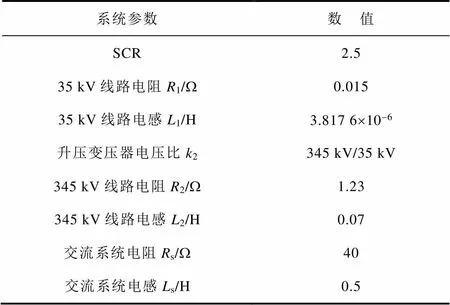
附表2 弱交流電網主要參數

2. 系統傳遞函數模型

式（10）～式（13）中傳遞函數具體表達式為

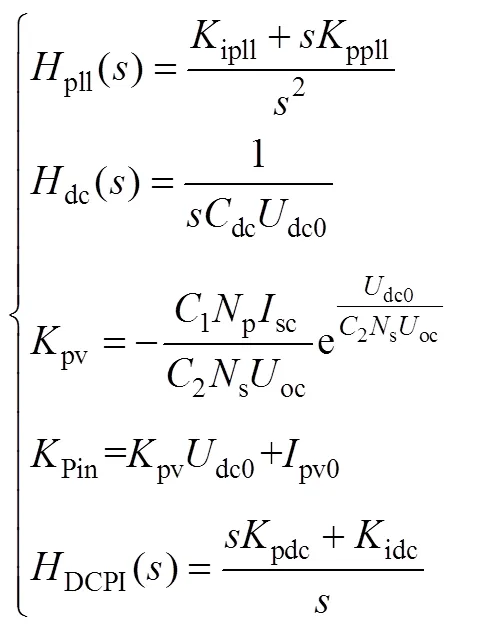
式中，sc、oc分別為標準測試條件下PV陣列的短路電流、開路電壓，均由生產廠家提供；系數1、2可由廠家參數求得。

根據式（14），LCL濾波器傳遞函數框圖如附圖1所示。圖中，網側換流器電流Dtd=Dgd+Dlcld、Dtq=Dgq。

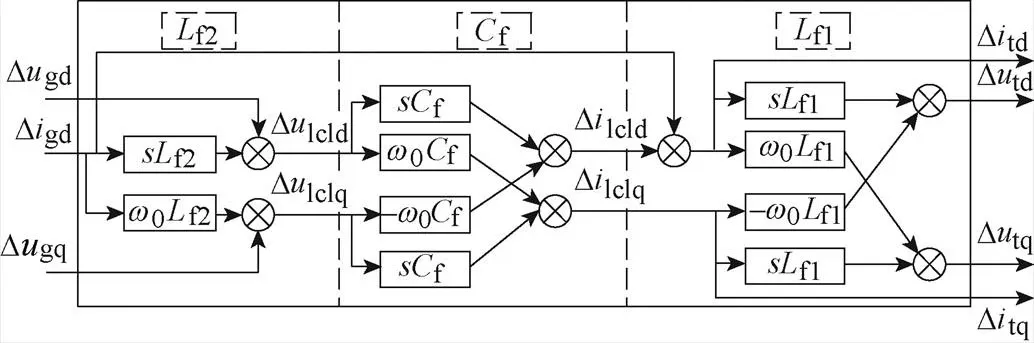
附圖1 LCL濾波器傳遞函數框圖

App.Fig.1 Transfer function block diagram of LCL filter

式（15）中傳遞函數具體表達式為

式（16）和式（17）中坐標變換傳遞函數表達式為

式（18）中傳遞函數具體表達式為

式（19）中傳遞函數具體表達式為

弱交流電網中式（20）的傳遞函數具體表達式為

式中，G、G分別為弱交流電網的等效電感和等效電阻，其表達式如式（A7）所示。

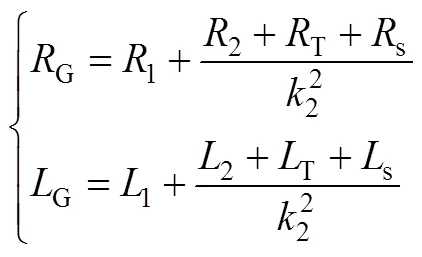
式中，2為二級升壓變壓器電壓比。

[1] 國家能源局. 2021年光伏發電建設運行情況[EB/OL]. [2022-03-09].http://www.nea.gov.cn/2022-03/09/c_ 1310508114.htm.

[2] 鄭超, 王士元, 張波琦, 等. 光伏高滲透電網動態頻率特性及應對措施[J]. 電網技術, 2019, 43(11): 4064-4073.

Zheng Chao, Wang Shiyuan, Zhang Boqi, et al. Dynamic frequency characteristics and counter- measures of power grid with highly penetrated photovoltaics[J]. Power System Technology, 2019, 43(11): 4064-4073.

[3] 張金平, 汪寧渤, 黃蓉, 等. 高滲透率光伏參與電力系統調頻研究綜述[J]. 電力系統保護與控制, 2019, 47(15): 179-186.

Zhang Jinping, Wang Ningbo, Huang Rong, et al. Survey on frequency regulation technology of power grid by high-penetration photovoltaic[J]. Power System Protection and Control, 2019, 47(15): 179- 186.

[4] 蔡紀鶴, 李蓓, 張永春. 基于SVPWM的光伏無功控制研究[J]. 電工技術學報, 2016, 31(24): 233-239.

Cai Jihe, Li Bei, Zhang Yongchun. Research on photovoltaic reactive power control based on SVPWM[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 233-239.

[5] 商皓鈺, 劉天琪, 卜濤, 等. 計及風電與光伏并網的電力系統運行風險評估[J]. 現代電力, 2020, 37(4): 358-367.

Shang Haoyu, Liu Tianqi, Bu Tao, et al. Operational risk assessment of power system considering wind power and photovoltaic grid connection[J]. Modern Electric Power, 2020, 37(4): 358-367.

[6] 張劍云. 哈密并網風電場次同步振蕩的機理研究[J]. 中國電機工程學報, 2018, 38(18): 5447-5460.

Zhang Jianyun. Research on the mechanism of subsynchronous oscillations of wind farms in Hami[J]. Proceedings of the CSEE, 2018, 38(18): 5447-5460.

[7] 薛安成, 付瀟宇, 喬登科, 等. 風電參與的電力系統次同步振蕩機理研究綜述和展望[J]. 電力自動化設備, 2020, 40(9): 118-128.

Xue Ancheng, Fu Xiaoyu, Qiao Dengke, et al. Review and prospect of research on sub-synchronous oscillation mechanism for power system with wind power participation[J]. Electric Power Automation Equipment, 2020, 40(9): 118-128.

[8] 張天翼, 王海風. 風電并入弱交流系統引發次同步振蕩的研究方法綜述[J]. 電力系統保護與控制, 2021, 49(16): 177-187.

Zhang Tianyi, Wang Haifeng. Research methods for subsynchronous oscillation induced by wind power under weak AC system: a review[J]. Power System Protection and Control, 2021, 49(16): 177-187.

[9] 謝小榮, 劉華坤, 賀靜波, 等. 直驅風機風電場與交流電網相互作用引發次同步振蕩的機理與特性分析[J]. 中國電機工程學報, 2016, 36(9): 2366- 2372.

Xie Xiaorong, Liu Huakun, He Jingbo, et al. Mechanism and characteristics of subsynchronous oscillation caused by the interaction between full- converter wind turbines and AC systems[J]. Pro- ceedings of the CSEE, 2016, 36(9): 2366-2372.

[10] Liu Huakun, Xie Xiaorong, He Jingbo, et al. Subsynchronous interaction between direct-drive PMSG based wind farms and weak AC networks[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4708-4720.

[11] Li Chun. Unstable operation of photovoltaic inverter from field experiences[J]. IEEE Transactions on Power Delivery, 2018, 33(2): 1013-1015.

[12] 陳武暉, 楊彥霽, 謝永勝, 等. 大規模光伏發電經串補并網系統次同步振蕩機制[J]. 電網技術, 2021, 45(12): 4711-4721.

Chen Wuhui, Yang Yanji, Xie Yongsheng, et al. SSO mechanism of large-scale PV generation connected to series-compensated power system[J]. Power System Technology, 2021, 45(12): 4711-4721.

[13] 高本鋒, 姚磊, 李忍, 等. 大規模光伏電站并網的振蕩模式分析[J]. 電力自動化設備, 2017, 37(8): 123-130.

Gao Benfeng, Yao Lei, Li Ren, et al. Analysis on oscillation modes of large-scale grid-connected PV power plant[J]. Electric Power Automation Equip- ment, 2017, 37(8): 123-130.

[14] 趙書強, 李忍, 高本鋒, 等. 光伏并入弱交流電網次同步振蕩機理與特性分析[J]. 中國電機工程學報, 2018, 38(24): 7215-7225, 7448.

Zhao Shuqiang, Li Ren, Gao Benfeng, et al. Analysis of mechanism and characteristics in sub synchronous oscillation between PV and weak AC networks[J]. Proceedings of the CSEE, 2018, 38(24): 7215-7225, 7448.

[15] 趙書強, 高瑞鑫, 邵冰冰, 等. 多光伏發電單元并入弱交流電網系統的站內/站網次同步振蕩特性分析[J]. 電力建設, 2021, 42(12): 49-58.

Zhao Shuqiang, Gao Ruixin, Shao Bingbing, et al. Inside-plant and plant-grid sub-synchronous oscilla- tion characteristics analysis of multiple PV generation units connected to a weak AC power grid[J]. Electric Power Construction, 2021, 42(12): 49-58.

[16] Du Wenjuan, Fu Qiang, Wang Haifeng. Method of open-loop modal analysis for examining the subsyn- chronous interactions introduced by VSC control in an MTDC/AC system[J]. IEEE Transactions on Power Delivery, 2018, 33(2): 840-850.

[17] 甄自競, 杜文娟, 王海風. 近似強模式諧振下高壓直流輸電系統引起的次同步振蕩仿真研究[J]. 中國電機工程學報, 2019, 39(7): 1976-1985.

Zhen Zijing, Du Wenjuan, Wang Haifeng. The simulation study on SSOs caused by the HVDC under the condition of near strong modal resonance[J]. Proceedings of the CSEE, 2019, 39(7): 1976-1985.

[18] 楊明, 周林, 張東霞, 等. 考慮電網阻抗影響的大型光伏電站并網穩定性分析[J]. 電工技術學報, 2013, 28(9): 214-223.

Yang Ming, Zhou Lin, Zhang Dongxia, et al. Stability analysis of large-scale photovoltaic power plants for the effect of grid impedance[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 214-223.

[19] 陳新, 張旸, 王赟程. 基于阻抗分析法研究光伏并網逆變器與電網的動態交互影響[J]. 中國電機工程學報, 2014, 34(27): 4559-4567.

Chen Xin, Zhang Yang, Wang Yuncheng. A study of dynamic interaction between PV grid-connected inverters and grid based on the impedance analysis method[J]. Proceedings of the CSEE, 2014, 34(27): 4559-4567.

[20] 張美清, 袁小明, 胡家兵. 基于自穩/致穩性的路徑級數展開方法及其在含多樣化電力電子裝備電力系統穩定性分析中的應用[J]. 中國電機工程學報, 2021, 41(5): 1637-1655.

Zhang Meiqing, Yuan Xiaoming, Hu Jiabing. Path series expansion method based on self-/en-stabilizing properties and its application in the stability analysis of power systems with diversified power electronic devices[J]. Proceedings of the CSEE, 2021, 41(5): 1637-1655.

[21] Huang Yunhui, Yuan Xiaoming, Hu Jiabing, et al. DC-bus voltage control stability affected by AC-bus voltage control in VSCs connected to weak AC grids[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(2): 445-458.

[22] Yuan Hao, Yuan Xiaoming, Hu Jiabing. Modeling of grid-connected VSCs for power system small-signal stability analysis in DC-link voltage control times- cale[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3981-3991.

[23] 高本鋒, 劉毅, 李蘊紅, 等. 直驅風電場與LCC- HVDC次同步交互作用的擾動傳遞路徑及阻尼特性分析[J]. 中國電機工程學報, 2021, 41(5): 1713- 1729.

Gao Benfeng, Liu Yi, Li Yunhong, et al. Analysis on disturbance transfer path and damping characteristics of sub-synchronous interaction between D-PMSG- based wind farm and LCC-HVDC[J]. Proceedings of the CSEE, 2021, 41(5): 1713-1729.

[24] Du W, Wang X, Wang H. Sub-synchronous inter- actions caused by the PLL in the grid-connected PMSG for the wind power generation[J]. International Journal of Electrical Power & Energy Systems, 2018, 98: 331-341.

[25] 高本鋒, 姚磊, 李忍. 弱電網下鎖相環對大型光伏電站振蕩模式的影響[J]. 太陽能學報, 2017, 38(12): 3302-3310.

Gao Benfeng, Yao Lei, Li Ren. Influence of phase- locked loop on oscillation modes of large-scale PV power plant in weak grid[J]. Acta Energiae Solaris Sinica, 2017, 38(12): 3302-3310.

[26] 劉巨, 姚偉, 文勁宇. 考慮PLL和接入電網強度影響的雙饋風機小干擾穩定性分析與控制[J]. 中國電機工程學報, 2017, 37(11): 3162-3173, 3371.

Liu Ju, Yao Wei, Wen Jinyu. Small signal stability analysis and control of double-fed induction generator considering influence of PLL and power grid strength[J]. Proceedings of the CSEE, 2017, 37(11): 3162-3173, 3371.

[27] 韓平平, 林子豪, 夏雨, 等. 大型光伏電站等值建模綜述[J]. 電力系統及其自動化學報, 2019, 31(4): 39-47.

Han Pingping, Lin Zihao, Xia Yu, et al. Review on equivalent modeling of large-scale photovoltaic power plant[J]. Proceedings of the CSU-EPSA, 2019, 31(4): 39-47.

[28] 董文凱, 任必興, 王海風, 等. 適用于系統次同步振蕩分析的風電場等值建模方法綜述[J]. 電力工程技術, 2022, 41(4): 33-43.

Dong Wenkai, Ren Bixing, Wang Haifeng, et al. Small-signal equivalent modeling methods of the wind farm and its application in sub-synchronous oscillations analysis of gird-connected wind power systems[J]. Electric Power Engineering Technology, 2022, 41(4): 33-43.

[29] 黃云輝, 翟雪冰, 劉棟, 等. 弱電網下風力發電機組并網變流器直流電壓穩定性機理分析[J]. 高電壓技術, 2017, 43(9): 3127-3136.

Huang Yunhui, Zhai Xuebing, Liu Dong, et al. Stability analysis on DC-link voltage of wind turbine grid-connected converter as integrated to weak grid[J]. High Voltage Engineering, 2017, 43(9): 3127-3136.

[30] 趙書強, 李忍, 高本鋒, 等. 適用于多源系統次同步振蕩分析的圖形化建模方法[J]. 電工技術學報, 2017, 32(14): 184-193, 228.

Zhao Shuqiang, Li Ren, Gao Benfeng, et al. A graphical modeling method applied for multi-sources system subsynchronous oscillation analysis[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(14): 184-193, 228.

[31] 徐衍會, 曹宇平. 直驅風機網側換流器引發次/超同步振蕩機理研究[J]. 電網技術, 2018, 42(5): 1556- 1564.

Xu Yanhui, Cao Yuping. Research on mechanism of sub/sup-synchronous oscillation caused by GSC con- troller of direct-drive permanent magnetic syn- chronous generator[J]. Power System Technology, 2018, 42(5): 1556-1564.

[32] 趙偉然, 汪海蛟, 李光輝, 等. 分布式光伏并網電壓和功率因數協調控制策略[J]. 電力工程技術, 2017, 36(6): 20-26.

Zhao Weiran, Wang Haijiao, Li Guanghui, et al. Voltage and power factor coordination control for distributed photovoltaic integration[J]. Electric Power Engineering Technology, 2017, 36(6): 20-26.

Analysis of Path and Damping Characteristics of Subsynchronous Interaction Between Photovoltaic Plant and Weak AC Grid

1122

（1. Hebei Key Laboratory of Distributed Energy Storage and Micro-Grid North China Electric Power University Baoding 071003 China 2. State Grid Hebei Electric Power Co. Ltd Electric Power Research Institute Shijiazhuang 050021 China）

When a large-scale photovoltaic (PV) plant is integrated into the AC grid through long transmission lines, the interaction between the PV plant and weak AC grid may make the integration face the threat of subsynchronous oscillation (SSO). However, the mechanism of the subsynchronous interaction between the PV plant and weak AC grid are unclear, and quantifying the damping characteristics of the subsynchronous interaction is difficult by the existing analysis methods. Therefore, this paper proposes a damping torque method extended to the dynamic equation of phase-locked loop (PLL) to analyze the subsynchronous interaction between the PV plant and weak AC grid.

Firstly, the damping torque method is extended to the PLL dynamic equation to analyze the stability of the PV plant integrated into the weak AC grid system in the SSO mode dominated by PLL. Secondly, the linearization model of the PV plant integration and its corresponding closed-loop transfer function block diagram are derived. Based on the closed-loop transfer function diagram, the coupling relationship and interaction path between the PV plant and weak AC grid are revealed from the perspective of internal disturbance transfer, and the dynamic process of the interaction path affecting SSO mode damping is analyzed. Thirdly, through transfer function derivation, the damping path reflecting the subsynchronous interaction is separated, and the equivalent damping coefficient is used to quantify the SSO mode damping of the subsynchronous interaction. Finally, the influences of PLL control parameters, PV capacity, AC grid strength, PV plant intensity, and temperature on the damping characteristics of subsynchronous interaction are analyzed.

The mechanism analysis shows that the PV plant-weak AC grid current disturbance and the grid-side voltage disturbance drive each other at the point of common coupling, forming the subsynchronous interaction path. Then, the subsynchronous interaction path will form a closed-loop damping path through the PLL in the SSO mode dominated by PLL, affecting the system SSO mode damping. Therefore, the damping contribution of the PV plant and subsynchronous interaction are quantitatively evaluated through the damping path separation. The results show that the PV plant and the subsynchronous interaction provide positive damping and negative damping to the system, respectively, resulting in the SSO of the PV plant integrated into the weak AC grid system. In addition, the subsynchronous interaction damping can be decreased by increasing the PLL proportion coefficient, AC grid strength, PV plant intensity or temperature, or decreasing the PLL integration coefficient or PV capacity, thereby improving the stability of the PV plant integrated to weak AC grid system.

The following conclusions can be drawn from the theoretical analysis: (1) The subsynchronous interaction between the PV plant and weak AC grid will form the damping path through the PLL, affecting the SSO mode damping of the system. There is the SSO risk dominated by PLL in the PV plant integration. (2) The subsynchronous interaction provides negative damping to the system, which is the dominant factor for the SSO of the PV plant integration. (3) Reasonable design of system parameters according to the negative damping characteristics of subsynchronous interaction can effectively increase the SSO mode damping and better maintain the original positive damping characteristics of the PV plant.

Photovoltaic plant, subsynchronous oscillation, subsynchronous interaction, damping torque method, phase-locked loop

TM712

10.19595/j.cnki.1000-6753.tces.221776

國家重點研發計劃資助項目“響應驅動的大電網穩定性智能增強分析與控制技術”（2021YFB2400800）。

2022-09-18

2022-10-26

高本鋒 男，1981年生，副教授，研究方向為高壓直流輸電和電力系統次同步振蕩。E-mail: gaobenfeng@126.com

鄧鵬程 男，1998年生，碩士，研究方向為新能源并網系統次同步振蕩分析。E-mail: 1533202670@qq.com（通信作者）

（編輯 郭麗軍）