基于穩定匹配的網約車合乘優化

彭子烜,魏 然,單文軒,王文思,郭 震,蔡婉君

(1.北京交通大學 交通運輸學院,北京 1000441; 2.北京航空航天大學 交通科學與工程學院,北京 102206;3.中國石化化工銷售有限公司 華南分公司,廣東 廣州 510620)

0 引 言

隨著“互聯網+”和共享經濟的蓬勃發展,網約車行業應運而生并迅速擴張。根據中國互聯網絡發展狀況統計調查,2016年末至2018年末,網約車用戶規模和用戶使用率進入增速迅猛期,截至2022年6月,我國網約車用戶規模達4.05億人,網約車用戶使用率達到38.50%。截至2023年1月,獲得網約車平臺公司獲得經營許可已有300多家。網約車的快速發展得益于優惠的價格、良好的乘車體驗和高效快速的需求響應。其中,如何快速匹配供需,及時對需求進行響應成為網約車可持續發展的關鍵。

當前越來越多的網約車平臺都推出了拼車服務,它們根據乘客提交的信息(起點,終點,時間),整合相似出行路徑的乘客給司機派單。在這種模式下,乘客和司機被動選擇接受或拒絕平臺的指派。然而,作為利己的乘客和司機,他們更關注如何使自身利益得到最大化,因此,司機對乘客存在選擇偏好(比如,司機更偏好搭載收益高的乘客),同理,乘客對司機也存在選擇偏好(比如,乘客更偏好與距離近的司機匹配)[1-3]。隨著偏好信息的納入,乘客和網約車匹配機制變得越來越重要。在網約車匹配中,如果忽視乘客和司機雙方的選擇偏好,不僅會降低他們的滿意度,還會影響他們進入匹配市場的動力。因此,有必要提出穩定的匹配機制,在穩定匹配下,任何乘客和司機都無法通過單方面改變匹配對象而獲得更高的效益,實現匹配的均衡。

近年來,國內外學者對網絡車合乘問題進行了大量的研究[1-3],一部分學者從系統最優視角出發,一部分學者則從均衡視角開展研究[4-5]。D.J. FAGNANT等[6]構建了以最小化乘客等待時間和車內時間為目標函數的網約車匹配模型;在N. AGATZ等[7]的研究中,目標函數是最小化車輛走行距離,通過隨機優化方法進行求解,相比于貪婪算法,匹配效率更高;侯立文等[8]建立了多目標合乘模型,分別為乘客效用最大化和司機總行程最小化;QIAN Xinwu等[9]的研究對象包括了出租車和網約車,根據主從博弈方法,研究了兩者的競爭關系和均衡狀態的存在性;WANG Xing等[2]立足于利己參與人視角,將穩定匹配概念引入到乘客和司機的匹配中,定義并驗證了匹配的均衡狀態;胡盼等[10]研究了選擇出租車出行的影響因素;周樂欣等[11]考慮了網約車定價均衡問題。

穩定匹配的概念是由D. GALE等[12]提出,并在多個領域均有所應用[13-16]。近年來,穩定匹配理論在交通領域得到了一定的應用和推廣。在停車匹配方面,HE Fang等[17]研究了車輛-車位穩定匹配問題,并對穩定匹配狀態進行了公式化描述,在價格的調整下,系統最優解也能夠滿足穩定匹配條件;在船貨匹配方面,PENG Zixuan等[18]研究了干散貨船-貨物穩定匹配問題,針對供需平衡、供大于求、供小于求3種場景,設計了價格博弈策略,實現匹配均衡和價格均衡;在航空領域,ZHANG Dapeng等[19]對航線-機場的匹配穩定問題進行研究。

筆者設計了考慮乘客和司機選擇偏好的雙邊穩定匹配,體現了乘客和司機希望能夠最大化自身利益,主要創新點在于:①在乘客和網約車的匹配中引入穩定性的概念,將乘客和司機的選擇偏好公式化;②在網約車匹配中考慮乘客合乘問題,應用沙普利值對合乘乘客的出行費用進行分攤,構建無偏好假設的多對一穩定匹配模型,并設計算法進行求解。

1 問題描述

在網約車運營中,供給方和需求方分別是司機和乘客。司機作為出行服務的提供者,在系統內的位置是已知的,每個司機可以選擇搭載一位或者多位乘客。乘客是出行服務的需求者,提供了起點、終點以及時間窗等出行信息。網約車平臺基于以上信息,將乘客進行分組并匹配相應的網約車。乘客分組如圖1(a)。圖1(a)中,圈內的乘客表示可以合乘出行。假設乘客希望匹配與自己距離近的司機,而司機希望搭載收益高的乘客組。表1展示了司機和乘客組的偏好排序情況。比如,司機1搭載乘客組1的收益要高于搭載乘客組3,因此,他把乘客組1排在第1位。

表1 乘客和司機的偏好排序

圖1 網約車合乘優化

根據以上信息,將乘客組和司機進行匹配。其中,司機1搭載乘客組3、司機2搭載乘客組2、司機3搭載乘客組1、司機4搭載乘客組4是一個可行匹配。但是這個匹配是不穩定的,因為司機1和乘客組1把彼此排在偏好排序的第一位,卻沒有匹配到一起,他們會拒絕系統指派,選擇私下匹配。筆者將司機1和乘客組1稱之為阻礙匹配對。而穩定匹配如圖1(b),司機到達乘客的起點,將乘客送達目的地。在該匹配中,不存在任何上述的阻礙匹配對。

2 基于穩定匹配的網約車合乘模型

為了便于理解匹配的穩定性,在問題描述中,假設乘客和乘客之間沒有選擇偏好,但是在實際中,一起合乘出行的乘客之間是存在相互影響的。因此,在構建網約車合乘模型時,打破原有假設,即文中司機對乘客組有偏好,而乘客則同時對司機和合乘乘客組合存在偏好。

2.1 乘客和司機的偏好排序

乘客作為利己的出行者,通常希望出行成本越小越好。當有司機d搭載乘客組ρ時,乘客i∈ρ的出行成本包括了車費和時間成本兩部分,如式(1);ρ中的乘客根據沙普利值進行車費分攤,如式(2):

Ci(ρ,d)=Fi(ρ,d)+γ×(TGi-ei) (?i∈ρ,?d∈D)

(1)

{ε×[l(s)-l(s′)]} (?i∈ρ,?d∈D)

(2)

式中:Ci(ρ,d)為司機d搭載乘客組ρ時,乘客i∈ρ的出行成本;Fi(ρ,d)為司機d搭載乘客組ρ時,乘客i∈ρ付給司機的車費;γ為乘客的時間成本;TGi為司機到達乘客i終點的時間;ei為乘客i的最早出發時間;ρ(i)為乘客組ρ中包含乘客i的所有子集形成的集合;ε為每公里車費單價;l(s)為服務乘客集合s時車輛的最短道路距離;s′為集合s中去除元素i后剩下元素的集合。

令(ρ,d)為一個匹配對,如果乘客i∈ρ在(ρ,d)中的出行成本小于在(ρ′,d′)中的出行成本,那么乘客i更偏好匹配對(ρ,d),乘客的偏好由式(3)表示:

(3)

然而,司機通常希望收益越高越好。當有司機d搭載乘客組ρ時,司機的收益如式(4);同理,司機的偏好由式(5)表示:

(4)

ρd>ρ′d,R(ρ,d)>R(ρ′,d)

(5)

式中:R(ρ,d)為司機d搭載乘客組ρ時的收益;ξ為司機每公里收益。

2.2 穩定匹配模型

網約車合乘不僅可以提高乘客的匹配率,還可以節約乘客的出行里程。而節約出行里程也有利于提高司機的收益。因此,文中目標函數是最大化乘客節約出行里程:

(6)

(7)

(8)

(9)

(10)

3 算法設計

為了對上述多對一穩定匹配模型進行求解,筆者基于DA(deferred acceptance)算法進行算法設計[12]。DA算法是求解穩定匹配問題的算法之一,該算法可以從任意偏好排序出發,通過請求和拒絕操作,產生一個穩定解。DA算法已廣泛地應用于交通問題中,如船貨匹配、共享停車匹配、網約車匹配等[9,17-18]。

筆者基于DA算法的思想,設計尋找穩定匹配解的具體流程如下:

Step1:生成初始匹配解:每個參與人自我匹配(匹配對象為自己本身)。

Step2:尋找匹配解:每個乘客i尋找當前還未被拒絕的排名最高的匹配方案。

Step3:尋找阻礙匹配對:遍歷每個乘客i和司機d的當前匹配解,尋找是否存在一個阻礙匹配對,如果存在,則該阻礙匹配對中每個參與者均被當前匹配方案拒絕,并轉入Step2,否則當一個匹配解中不存在任何阻礙匹配對時,算法結束。

4 案例分析

筆者以大連市為依托進行了算例設計,以驗證模型和算法的有效性。大連市路網長402 km,共有個228個節點和383個路段。基于大連市出租車GPS數據得到了乘客的起點和終點以及最早出發時間。由于乘客的時間窗無法獲得,假設乘客靈活時間分為兩種,一種是緊時間窗,以(0,15)min均勻隨機生成,一種是松時間窗,以(5,30)min均勻隨機生成。最晚到達時間等于最早出發時間、起終點間的出行時間和靈活時間之和。假設每輛車最多載3位乘客,車速為30 km/h,單位運營成本為0.5元/km。運價為2元/km,乘客的時間成本為26元/h(即大連市人均稅前收入除以每月工作小時數)。

4.1 小規模算例

為了說明匹配的過程,首先設計了一個包含2個司機和6個乘客的小規模算例,如圖2。假設乘客的時間窗為松時間窗。基于以上信息,可以生成25個匹配對,如表2。以匹配對6為例,司機1匹配乘客1和乘客5。根據司機和乘客在各個匹配對下的收益和成本,得到偏好排序如表3。以司機1為例,最偏好的是匹配對12,即{司機1,乘客1,乘客2,乘客3}。基于偏好排序,計算車輛的載客能力分別為1、2和3時的匹配結果。

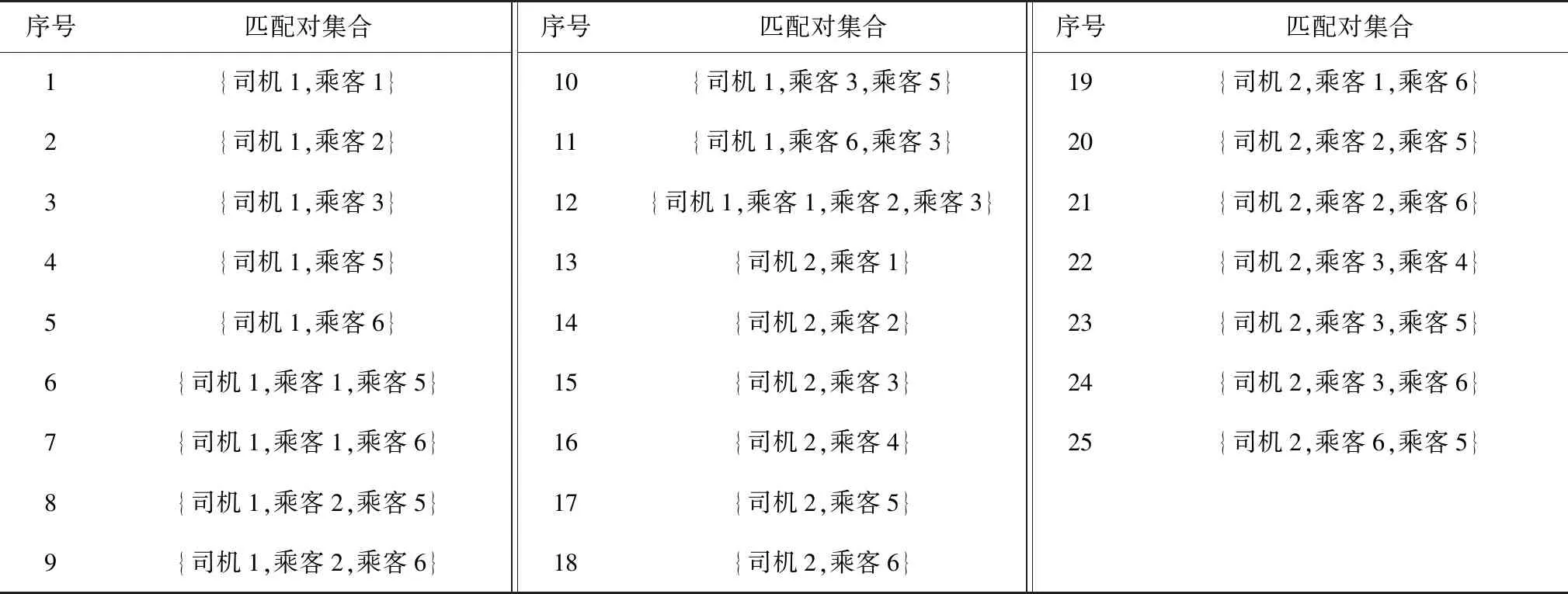
表2 匹配對集合

表3 乘客和司機對匹配對偏好排序

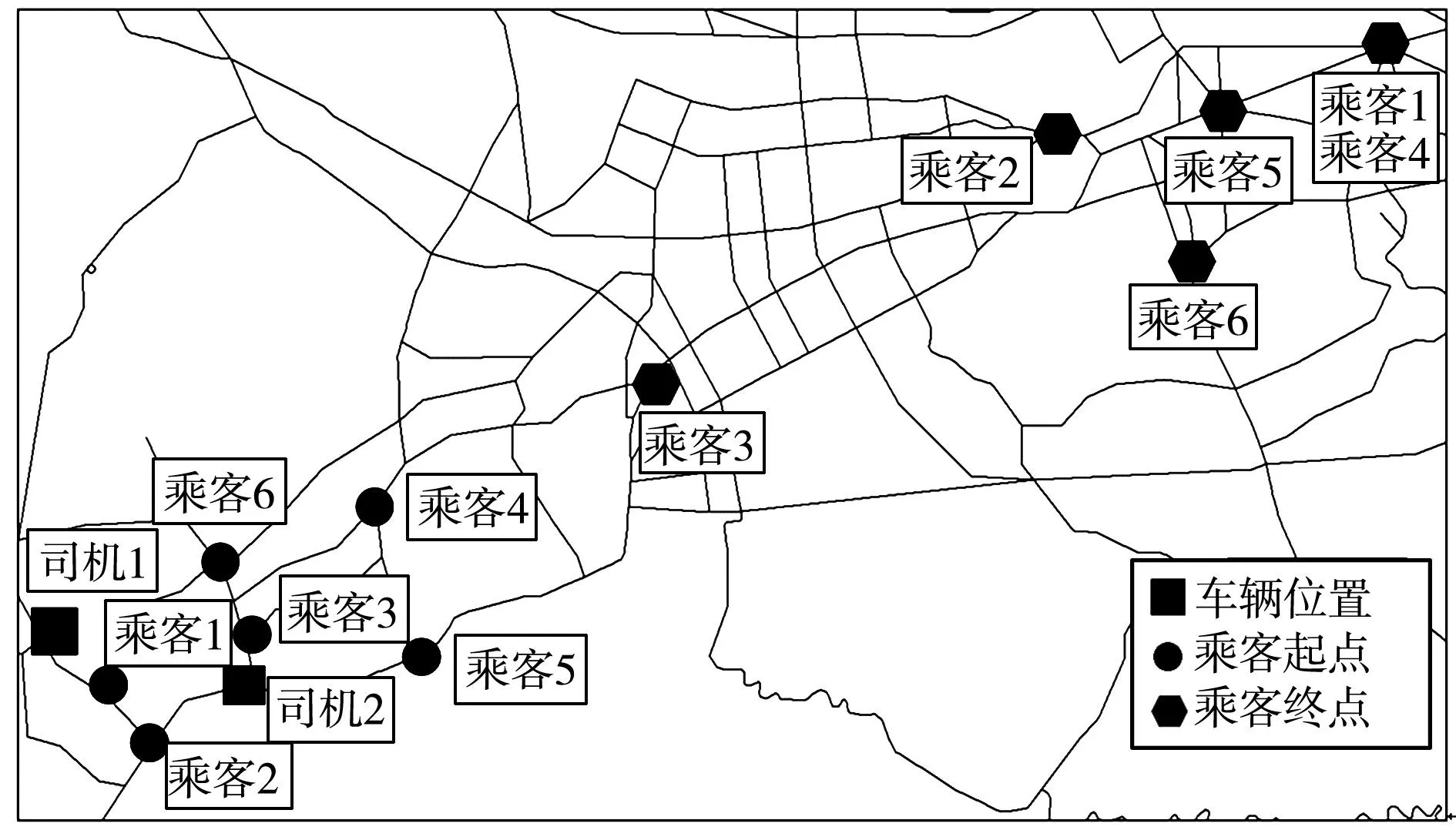
圖2 小規模算例

當車輛的載客能力為1時,匹配結果如圖3(a)。司機1匹配乘客1,司機2匹配乘客2。由于司機的數量少于乘客的數量,在非合乘下,司機更偏好搭載長距離的乘客。通常,長距離的乘客帶來的收益更高。當車輛的載客能力為2時,司機1匹配乘客1和乘客5,司機2匹配乘客2和乘客6,如圖3(b)。如果司機2搭載乘客3和乘客4,司機1匹配對象保持不變,這也是一個匹配解,但是該解不穩定。因為根據式(9),這個解會被匹配對21所阻礙。當車輛的載客能力為3時,匹配結果如圖3(c),即司機1匹配乘客1、乘客2和乘客3,司機2匹配乘客5和乘客6。乘客4由于時間窗限制沒有匹配到司機。乘客4僅參與到匹配對16和22中,但是包含這兩個匹配對的解均不穩定。綜上所述,以上匹配解均是穩定的,即沒有乘客或者司機能夠通過單方面改變匹配對象獲得更高的效益。

4.2 不同規模算例

筆者設計了不同規模的算例,算例的需求分為低需求(A)和高需求(B),算例包含了司機的數量,乘客的數量和時間窗。如300-600-r代表算例中有300 位司機和600位乘客,乘客時間窗為松時間窗。不同規模算例的計算結果如表4。首先,從時間窗的角度進行結果分析,松時間窗下乘客的匹配率較高,同時乘客合乘比例也有所增加。這是因為乘客的時間窗松弛后,降低了時間約束的影響,增加了乘客合乘的可能性,乘客匹配率平均提高18%,合乘比例平均提高21%。乘客合乘有利于增加司機的平均收益,但是隨著乘客合乘的比例增加,乘客的平均等待時間也有所增加,同時可能發生一些不可避免的繞行,使得繞行比例增加。然后分析低需求(A)和高需求(B)下的計算結果,需求增加了兩倍后,司機匹配率增加,乘客合乘的比例有了大幅提升,同時司機的收入也有所提高。乘客的需求影響了合乘的可能性,參與的乘客越多,合乘的可能性就越大。

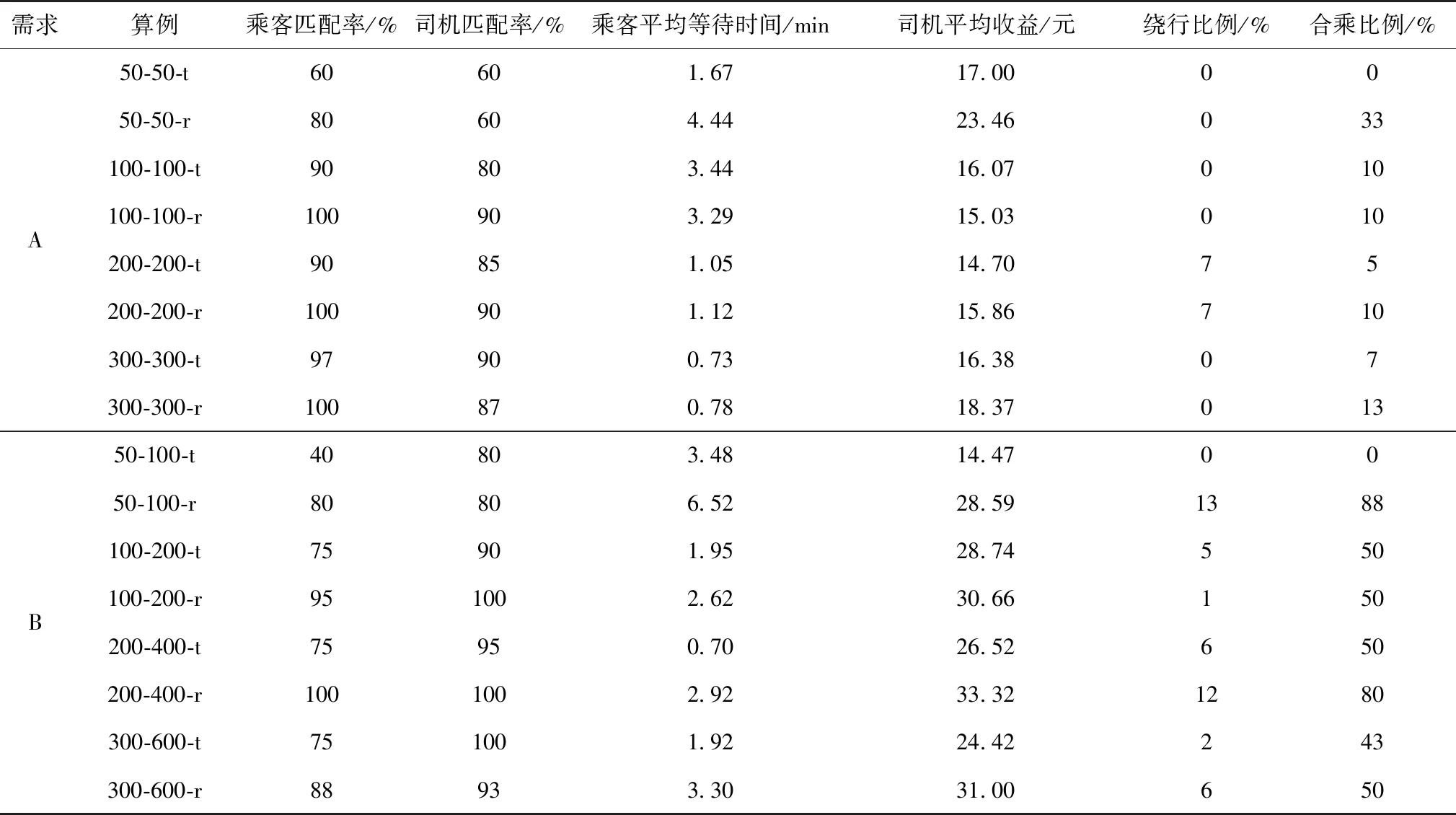
表4 不同規模的計算結果

5 結 論

筆者在研究網約車合乘問題時,考慮了利己乘客和司機希望實現自身利益的最大化,基于合乘乘客間的相互影響,構建了多對一穩定匹配模型并設計了相應的算法和不同規模的算例進行分析,得到以下主要結論:

1)提出合乘模式下乘客和司機穩定匹配模型。通過計算結果可得,非合乘模式下,司機受收益驅動更偏好于搭載出行距離較長的乘客。在供給小于需求時,出行距離相對較短的乘客處于劣勢地位,出行需求難以被滿足。合乘模式下,隨著載客能力的提升,乘客的匹配率增加,但由于合乘出行時繞行不可避免,在時間窗的約束下,部分乘客合乘出行受限。在有限運力下,合乘模式可以增加乘客的匹配幾率,減少乘客總出行里程,降低碳排放。

2)時間窗和參與人數量對合乘模式下的匹配率尤為重要。隨著乘客時間窗的松弛,形成了更多的合乘出行方案,乘客匹配率平均提高18%,合乘比例平均提高21%。同時,高需求放大了乘客匹配率和合乘比例的提升幅度,與低需求相比,高需求下的提升比例是低需求的2倍之多。在打車需求旺盛時段,是可以通過合乘緩解打車難題,而且高的需求也為合乘提供了有利條件,乘客可以通過釋放一定時間窗要求以提高匹配的概率,降低等待時間。