電磁效應下耦合時滯神經元動力學分析
何沛妍,楊麗新,黨元辰,顧梓玉
(陜西科技大學數學與數據科學學院,陜西 西安 710021)
0 引言
對于自然界中生命體的生存和活動來說,神經系統是重要的信息中心,神經元作為神經系統的基本組成單元,對神經信息的傳導和控制至關重要[1-2],不同的外界刺激條件對神經元的放電節律會產生不同的影響[3],神經元之間的信息傳遞也會產生豐富的動力學行為[4-5].若神經系統沒有受到任何擾動與輸入信號的作用,則對應的輸出量會保持在某一狀態上;神經系統也可以在相應的控制中將神經元活動輸出為特定行為,Rinzel等[6]發現這些行為的差異是由于興奮性的分岔機制不同,其產生的分岔類型決定了神經元的計算特性[7],因此,神經系統的穩定性和分岔問題備受關注.
在對神經元深入學習的過程中,神經元數學模型的豐富與完善對神經系統的研究有推進意義.1961年,Fitzhugh和Nagumo等[8-9]對Hodgkin-Huxley(HH)模型[10]進行簡化,提出FHN模型,它可以模擬多種神經元行為[11].Bashkirtseva等[12]用隨機靈敏度函數法分析了FHN模型的興奮性,發現噪聲引起的模型動力學變化可以用其吸引子的高隨機敏感性來解釋.大多數情況下,神經元處于的環境復雜,離子在細胞膜內外運動與傳輸時,會導致細胞內外電磁場分布改變,產生電磁效應,大多數研究采用磁通量來刻畫.Ge等[13]研究了FHN神經元系統在電磁感應作用下高頻刺激驅動的弱低頻信號所產生的振動共振現象、集體行為等.文獻[14]研究了ML神經元模型在磁場的作用下簇放電的類型及分岔過程,討論了適當的耦合連接對神經元之間放電模式轉遷的作用.然而,在生物和人工神經系統中,時間延遲是普遍存在的,會使系統產生更加復雜的動力學行為[15].文獻[16]提出了一種帶有時滯的FHN耦合神經系統,發現信號傳輸的時間延遲對于FHN神經系統中同步尖峰的發生至關重要.文獻[17]考慮了神經元內外電磁場分布所產生的電磁效應,并討論了神經元系統所產生的動力學行為,揭示了電磁刺激對神經元系統的動力學行為有調控作用,但其沒有考慮到時間延遲在系統中的影響.
基于上述研究,本文同時考慮電磁效應和時滯,建立新的耦合FHN模型,借助時域法研究電磁效應下系統所產生的動力學行為,利用Routh-Hurwitz判據來判斷系統的穩定性,利用中心流形定理和規范型理論來分析系統所產生周期解的穩定性,并進行數值模擬,討論在不同條件下,施加電流刺激對系統穩定性的影響.
1 模型描述
1961年,Fitzhugh等建立了FHN神經元模型,可以表示為[18]
(1)
其中:x,y分別表示FHN神經元的膜電位和恢復變量;ε,a和b均表示為常數.
近年來,許多研究者對FHN神經元模型動力學行為進行了探索.其中,文獻[19]僅僅對單個神經元的動力學行為進行了討論,而耦合是神經元之間的連接橋梁,可以實現信號和能量的傳遞.文獻[20]分析的對象是兩個神經元耦合的神經系統,但其忽略了電磁效應的影響.因此,本文考慮神經元中電磁場分布改變產生的電磁效應以及神經元在傳遞和處理信息過程中產生的時間延遲,將兩個FHN神經元耦合,并且引入兩個時滯,建立了電磁效應下帶有時滯的耦合FHN模型:
(2)
其中:x1,x2表示兩個神經元的膜電位;y1,y2表示兩個神經元的恢復變量;φ表示在電磁效應下通過兩個神經元之間的磁通量;ρ(φ)表示憶阻器的記憶電導[21],并且ρ(φ)=α+3βφ2,α表示恒定的電導,β表示磁通反饋率;k1,k2,k3表示反饋增益;Iext1,Iext2表示神經元上的外部刺激電流;τ1,τ2表示時滯.
2 平衡點的穩定性分析
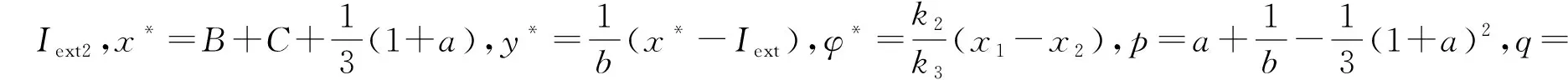
對系統(2)作變換:u1=x1-x*,v1=y1-y*,u2=x2-x*,v2=y2-y*,w=φ-φ*,則可得其線性化部分為
(3)
其中:A=(1+a)2x*-3(x*)2-a-k1ρ(φ),B=-1,E=k1ρ(φ),G=ε,H=-εb,J=k2,K=-k2,L=-k3.
并將系統(3)改寫為向量的形式為
(4)
其中u=(u1,v1,u2,v2,w)′,
若u=me-λt(m≠0)是系統(4)的解,則m(λI-A1-A2e-λτ1-A3e-λτ2)=0,其特征方程為
λ5+P1λ4+P2λ3+P3λ2+P4λ+P5+(P6λ2+P7λ+P8)e-λ(τ1+τ2)=0,
(5)
其中:P1=-2(A+H)-L,P2=2AH-2BG+(A+H)2+2L(A+H),P3=2(A+H)(-AH+BG)-(2AH-2BG)L-L(A+H)2,P4=A2H2+B2G2+(A+H)(2AHL-2BGL),P5=-A2H2L-B2G2L,P6=-GE2,P7=GHE2+GE2L,P8=-GHE2L.
在平衡點Q*(x*,y*,x*,y*,φ*)處,時滯τ1,τ2對系統(1)穩定性的影響分為τ1=τ2=0和τ1+τ2=τ>0兩種情況來討論[22].
當τ1=τ2=0時,特征方程變為
λ5+O1λ4+O2λ3+O3λ2+O4λ+O5=0,
(6)
其中:O1=P1,O2=P2,O3=P3+P6,O4=P4+P7,O5=P5+P8.由Routh-Hurwitz判據[23]可以得到:若Hi>0(i=1,2,3,4,5),特征值λ的實部均為負數,則系統(3)是局部漸進穩定的.其中Hi為特征方程的系數所構成的矩陣.
當τ1+τ2=τ>0時,特征方程變為
λ5+P1λ4+P2λ3+P3λ2+P4λ+P5+(P6λ2+P7λ+P8)e-λτ=0.
(7)
假設方程(7)有純虛根λ=wi(w>0),則
w5i+P1w4-P2w3i-P3w2+P4wi+P5+(-P6w2+P7wi+P8w)e-wτi=0.
(8)
分離方程(8)的實部和虛部為
(9)
其中ai(i=1,2,3,4,5,6)是關于w的多項式,a1=P1w4-P3w2+P5,a2=-P7w,a3=-(P6w2-P8),a4=w5-P2w3+P4w,a5=P6w2-P8,a6=-P7w.
由方程組(9)可以得到
(a2a4-a1a5)2+(a1a6-a3a4)2-(a2a6-a3a5)2=0.
(10)
若方程(9)中存在一個正實根w0,從方程(9)解得
(11)
令λ(τ)=α(τ)+w(τ)i是方程(7)在τ=τ0的一個根,并且滿足α(τ0)=0,w(τ0)=w0,可得
(12)
因此,當τ=[0,τ0),系統(1)在平衡點Q*(x*,y*,x*,y*,φ*)處是局部漸近穩定的;當τ=τ0時,系統(1)在平衡點Q*處產生了Hopf分岔;當τ>τ0時,系統(1)在平衡點Q*處不穩定.
3 周期解的穩定性分析
通過對系統(1)在平衡點Q*(x*,y*,x*,y*,φ*)處的穩定性分析,發現在τ0處會存在Hopf分岔,將規范型理論和中心流形定理[25]相結合來討論周期解的性質.

(13)
令Y(t)=(u1,v1,u2,v2,w)T,系統(13)記為Y′(t)=(τ0+ρ)A1Y(t)+(τ0+ρ)A4Y(t-1).
對于φ=(φ1,φ2,φ3,φ4,φ5)T∈C([-1,0],R5),定義有界線性算子Lρ(φ)和非線性算子f(ρ,φ)分別為
Lρ(φ)=(τ0+ρ)A1φ(0)+(τ0+ρ)A4φ(-1),
(14)
f(ρ,φ)=(τ0+ρ)(f1,f2,f3,f4,f5)T,
(15)
(16)
(14) 式中:
(15)式中:
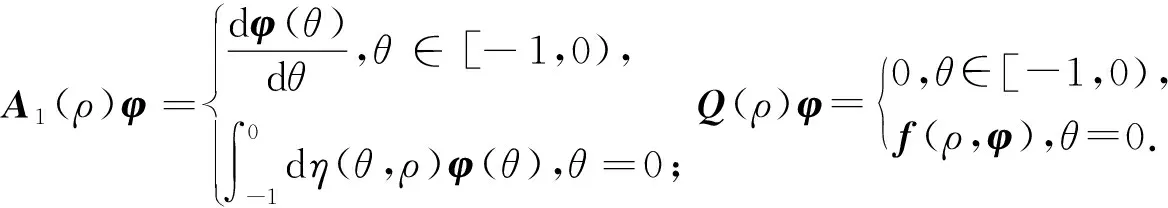
(17)
(18)
對于ψ∈C1([0,1],(R5)*),η(θ)=η(θ,0),定義伴隨線性算子A*和雙線性內積〈ψ(s),φ(θ)〉為:
(19)
(20)

(21)
(22)
(23)
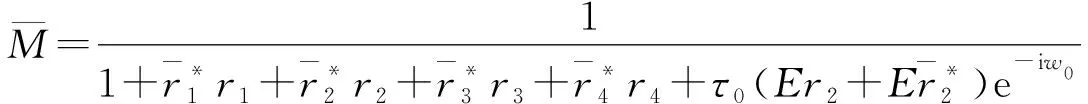
根據中心流形定理,可以得到
(24)
其中:
綜上所述,可以得到:
其中:μ2決定Hopf分岔的方向,β2決定分岔周期解的穩定性,T2決定分岔周期解的周期[26].
4 數值模擬
將分岔參數與輸入信號相結合來研究時滯和施加電流刺激對系統(1)的影響,取系統的初始狀態值為(0.43,0.02,0.03,0.4,0.5),設定系統中各參數的值為a=0.5,b=0.9,ε=1.5,k1=15,α=6.8,β=1,k2=-1.7,k3=1.在所取參數條件下,可得系統(1)的平衡點為(0,0,0,0,0).通過計算可以得到g20=g11=g02=0.019 0+0.007 9i,g21=-0.016 3+0.001 7i,λ′(τ0)=-0.129 2-0.156 9i,則C1(0)=-0.007 5+0.000 2i.由上節對Hopf分岔分析可以得到:μ2=-0.058 0<0,β2=-0.015 0<0,T2=-0.028 6<0,系統會發生亞臨界Hopf分岔,存在分岔周期解,并且分岔周期遞減.
首先分析未施加電流刺激時帶有時滯的耦合神經元系統放電行為.
當τ1=τ2=0時,系統(1)在零平衡點是漸進穩定的,如圖1所示,系統中狀態變量的時間變化曲線從初始狀態有小幅度波動,在t=5時刻趨近于(0,0,0,0,0).
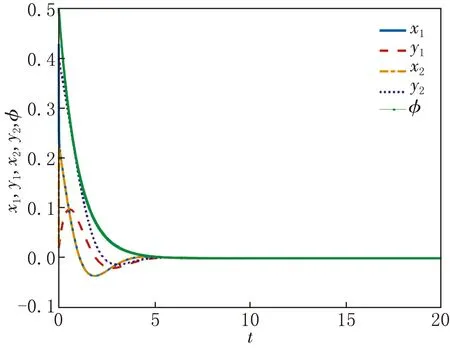
圖1 τ=0時系統(1)的時間序列圖
當τ1+τ2=τ>0時,由方程(12)可得w的一個正實值w0=0.382 4,可以得到系統的一組臨界時滯為τj=0.850 4,17.281 4,…(j=0,1,2,…).
當τ=0.450 4<0.850 4時,時滯對系統的影響不大,系統在零平衡點是漸進穩定的,如圖2所示.神經元系統的狀態變量在時滯的作用下出現振蕩,但在一定的時間內會趨近于零平衡點,維持穩定;當τ=0.850 4時,系統在零平衡點附近振蕩,失去了穩定性,呈現出周期放電狀態,系統是混沌的,如圖3所示.從系統(1)的狀態變量所對應的相圖可以看出,系統存在混沌吸引子.
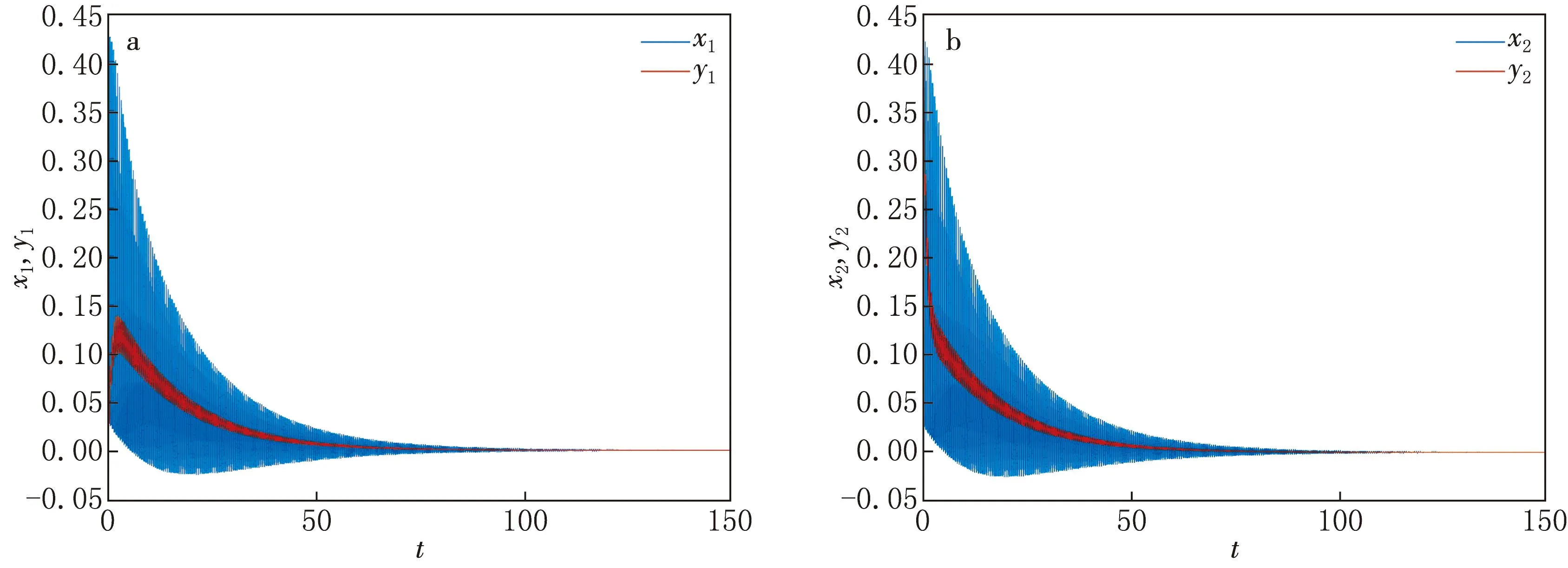
圖2 τ=0.450 4時系統(1)的狀態變量隨時間演化歷程圖
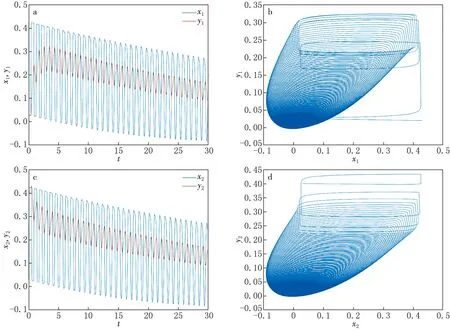
圖3 τ=0.850 4時系統(1)的狀態變量隨時間的演化歷程圖及平面內的相圖
由于帶有時滯的耦合FHN神經元系統在臨界時滯處發生亞臨界Hopf分岔,會導致系統的平衡失去穩定性,因此,施加電流刺激來控制系統的放電行為,研究電流刺激對系統產生的影響,在不同時滯下,改變Iext1,Iext2的值,所施加的刺激電流單位為mA·(cm2)-1.
當τ=0時,施加電流刺激,系統的平衡點會發生改變,而平衡狀態不會發生改變,如圖4所示.當τ=0.850 4時,若對系統中一個神經元施加電流刺激,如圖5(a)和(b)所示,系統的狀態變量的振蕩區域發生改變,系統放電狀態的周期發生變化;若對系統中兩個神經元同時施加電流刺激,神經元系統的狀態變量在振蕩之后會趨于平穩,如圖5(c)所示,狀態變量的平衡點也發生改變.該神經元系統從周期放電模式轉化為靜息狀態,系統穩定.因此,時滯和電流刺激的變化會對系統的動力學行為產生影響,施加電流刺激可以改變系統的混沌狀態.
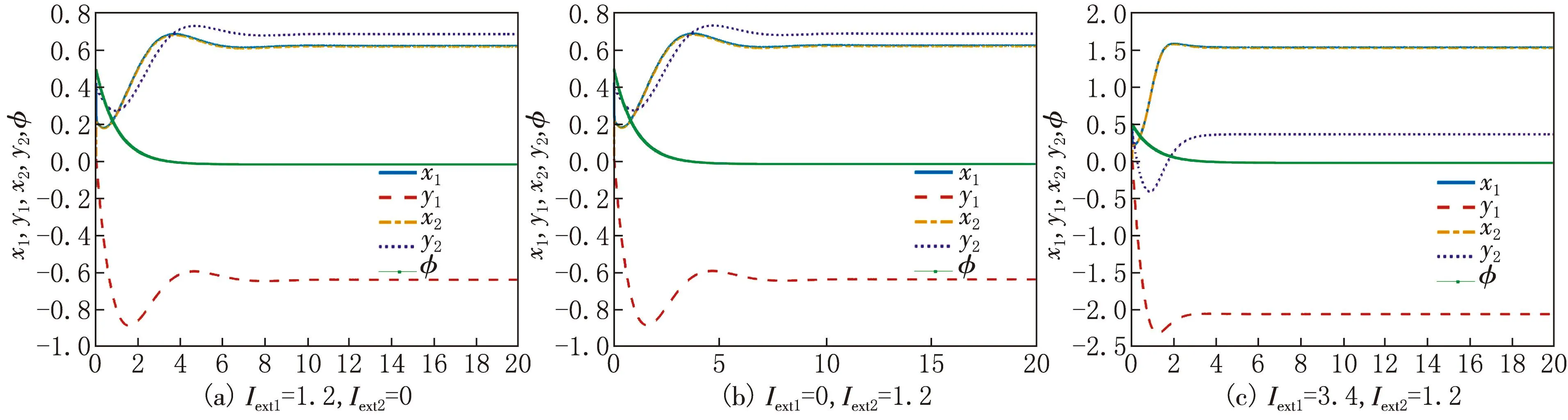
圖4 τ=0時施加不同的電流刺激,系統(1)的時間序列圖
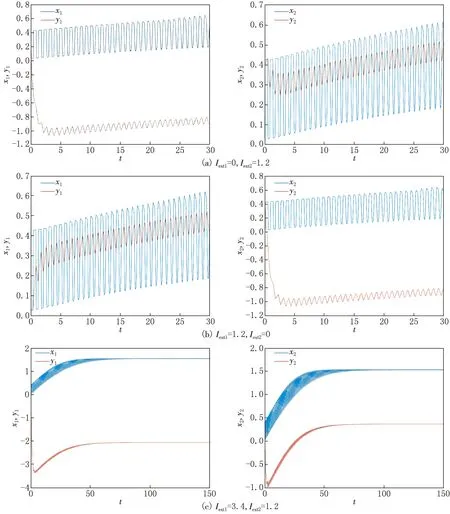
圖5 τ=0.850 4時施加不同的電流刺激,系統(1)的狀態變量隨時間的演化歷程圖
5 結論
本文基于FHN神經元模型,考慮了神經元之間信息傳遞所產生的時間延遲和神經元內外電磁場分布變化,建立了在電磁作用下帶有時滯的耦合FHN神經元模型.利用時域法研究了Hopf分岔的存在及其性質,分析了時滯與電流刺激對神經元系統的動力學影響.通過對該模型在平衡點處穩定性的討論,發現τ0=0.850 4是臨界時滯,當τ<τ0時,神經元系統在平衡點處漸近穩定;當τ>τ0時,產生了亞臨界Hopf分岔,系統失穩,在平衡點附近發生振蕩.當對其中一個帶有時滯的神經元施加一定的電流刺激時,該神經元的振蕩幅度減小;當對該模型中的兩個神經元同時施加電流刺激時,該模型從周期放電模式躍遷為靜息狀態,從振蕩狀態轉變為漸近穩定,并且平衡點位置發生改變.從上述結論可以得到,時滯對神經元系統的動力學行為有一定的影響,施加相應的電流刺激會調控系統的機制,維持系統的穩定狀態,這對利用合理的外部刺激方式來治療某些精神疾病提供了理論指導.

