概率基多目標優化在化工機械正交試驗及穩健設計中的應用

于 潔 賈 璞 肖超妮 鄭曉暉

（西北大學生命科學學院）

優化問題是實際的工程和日常生活中經常會遇到的問題，隨著社會發展和技術進步，優化問題所涉及到的因素和需求越來越多，越來越復雜。 許多優化問題往往需要同時考慮多個目標或屬性，屬于多目標優化問題。 多目標優化問題，在一定程度上應該歸屬于系統科學類問題。 以系統論的觀點，將多目標問題視為一個系統，進行整體優化，才能使系統在整體上達到最優，而各個目標之間在系統的整體優化的旗幟下達到某種協同或者折中。

目前，常用的多目標算法，主要有線性加權法、帕累托解法和ε-約束法，以及機械設計和選材的層次分析法 （AHP）， 多準則妥協解排序法（VIKOR），理想解相似度排序法（TOPSIS），基于比值分析的多目標優化法（MOORA）等。 但這些方法仍然存在一些基本問題，如：線性加權法中涉及到的權重因子和歸一化因子的確定依據不明確； 帕累托解法只能給出解的一個集合；ε-約束法只挑選出其中某一目標進行優化，而其他目標則作為約束條件進行處理，也就是將多目標優化問題降級為單一目標的優化問題等。 此外，從集合論和概率論的角度來看，線性加權法就是對幾個目標的集合進行并集運算，這顯然不符合多個目標同時優化應該是幾個目標的集合之交集運算的科學內涵。 因此，要解決多目標優化問題，就需要以系統論的觀點從整體上深刻揭示多目標優化的本征內涵，以各個目標之間的內在關系為導向，從系統工程的角度，探討多目標優化的異質同型的系統性，建立普適的各個多目標之間統籌兼顧的系統模型，并在應用中加以發展。

近年來，ZHENG M S等以系統論的觀點出發，從集合論和概率論的角度分析了多目標優化問題，建立了全新的概率基多目標優化方法［1］。筆者將概率基多目標優化方法應用于化工過程及機械設計的多目標優化問題，必將有助于恰當解決化工機械設計和加工方面的問題，得到科學和理性的結果。

1 概率基多目標同時優化方法的正交試驗設計步驟

1.1 概率基多目標優化方法簡介

概率基多目標優化方法（Probability-based Multi-Objective Optimization，PMOO） 企望解決以往多目標優化方法中存在人為（或主觀）因素的固有問題［1］。該方法以系統論的觀點，引入了青睞概率這一概念，來反映候選對象在優化過程中被青睞的程度，并將候選對象的所有性能效用指標劃分為效益型和成本型兩種基本類型。 效益型指標具有越大越好的特征，成本型指標具有越小越好的特征。 各候選對象的每個性能效用指標都定量地貢獻出一個分青睞概率。 從概率論的觀點來看，候選對象的總青睞概率就是其所有分青睞概率的乘積，這是它在優選過程中整體性和唯一的決定性指標。

在新的概率基多目標優化方法中，候選對象的效益型性能指標的效用值以正線性相關的方式貢獻其分青睞概率，即：

其中，Xij是第i個候選對象的第j個 （效益型）性能指標的效用值；Pij為該效益型性能指標的效用值Xij的分青睞概率；n是相關候選對象組中候選對象的總數；m是該組中每個候選對象的性能指標（目標）的總數；αj是候選對象的第j個效用性能指標的歸一化因子，αj=1/（nμj），μj是該效益型性能指標的效用值在所涉及的對象組中的算術平均值。

對于成本型性能指標， 可以進行對等地處理，以負線性相關的方式貢獻其分青睞概率，即：

其中，Xjmax和Xjmin分別表示對象組中該性能指標效用值的最大值和最小值，βj是第j個性能指標的效用值的歸一化因子，且βj=1/［n（Xjmax+Xjminμj）］。

此外，從概率論的角度看，對于多目標的“同時優化”，第i個候選對象的總（綜合）青睞概率Pi是其所有分青睞概率Pij的乘積，即：

候選對象的總青睞概率在整個優選過程中作為唯一的決定性指標，通過它就將多目標優化問題轉化為一個單目標優化問題。 新的概率基多目標優化的主要特點是對于效益型效用指標和成本型效用指標進行對等處理，而且在整個處理過程中不涉及人為（或主觀）的標度因子。

1.2 概率基多目標優化方法與正交試驗設計的結合

由于通過候選方案的總青睞概率能夠將多目標優化問題轉化為單目標優化問題，而且按照概率論，總青睞概率就是多個目標同時優化中唯一的、全面的決定性指標，因此就可以對總青睞概率進行正交試驗設計的極差分析，再由極差分析所得到的結果來確定相應的最佳配置。 這個操作程序就構建了概率基多個目標同時優化的正交試驗設計方法。

1.3 概率基多目標優化方法的穩健性設計

早在1950年，田口玄一就意識到可以通過穩健性（Robust，魯棒）設計來提高產品的質量，并且提出可以通過降低噪聲影響的方式來進行優化，這就是田口方法［2］。在田口方法中，將影響因素分為可控和不可控因素，他指出可以通過設計實驗來研究可控和不可控因素對響應的影響。 田口玄一所稱的不可控因素就是噪聲因素。 穩健性設計的思想是關于一組可控因素的設計，在最優點處產品的質量對所謂的噪聲因素具有不敏感性，或具有最小的噪聲影響。 在田口方法中，還進一步假設可控因素主要指那些實驗者或生產者容易控制的因素， 比如在注射成型過程中材料的選擇、注射成型時間及模具溫度等，而噪聲因素是那些不容易或非常昂貴或不可能控制的因素。 因此， 穩健性設計就是尋找到一套產品和工藝參數，使在該參數處產品的最終質量響應指標對不可控因素的變化具有最小敏感性，而不需要設法消除不可控因素。 進一步，田口玄一引入了“信噪比（SNR）”一詞來實施其穩健性設計，可控因素的最佳設計值就對應于信噪比最大值的狀態。 田口玄一還給出了3種標準類型的信噪比。 對于以目標值的期望值為優化點的情形有：

然而，文獻［3～7］的研究表明，在實際的實驗過程中， 通常實驗測試到的結果的平均值μ和標準差σ是一組互相獨立的響應。 但是，式（4）中信噪比SNR的表達式將這兩個響應（μ和σ）固化成為一個信噪比（SNR）響應，這是不合理的。 并且，SNR的最大值的優化不等價于同時使σ達到最小、使μ接近于其目標的優化。 更為嚴重的是，在具有“越小越好”和“越大越好”特征問題的表達式中，甚至標準差σ并未出現。這一點經常受到統計學家的批評［3～7］。

另外，統計學家們建議，可以通過使用兩個單獨的模型來考慮均值μ和標準差σ的響應。 因此， 對于σ的最小值和μ接近于其目標的優化，應該同時采用單獨的模型來處理，以達到合理的穩健性優化設計之目的。

這里，按照概率論的方法，以候選對象（方案）性能指標的算術平均值及其標準差作為處理中的兩個獨立響應，便可實施穩健性設計和產品的工藝優化［1］。

2 概率基多目標優化方法在化工機械設計中的應用實例

2.1 應用于管殼式換熱器折流板結構參數優化的正交試驗設計

管殼式換熱器廣泛應用于石油、化工及冶煉等領域，具有諸多優點，如結構簡單、安全可靠及傳熱效率高等。 管殼式換熱器中的折流板是不可缺少的工作部件，它會影響換熱器的傳熱、流動特性，以及殼程壓降等行為。

李德濤等對折流板的缺口高度h在殼程圓筒內徑的20%～45%范圍內進行設計，發現折流板缺口高度的變化會對流體的流動狀態產生影響，進而對其傳熱效率造成影響，而且換熱系數和殼程壓降會隨著折流板缺口高度的增大而減小，折流板的最小間距應不小于殼體內徑的1/5 也不應小于50 mm。研究表明，折流板間距越大殼程傳熱系數越小、壓降越小。 實際上，折流板間距應該有其最佳的參數值，故針對管殼式換熱器進行了優化設計［8］。 管殼式換熱器殼程內徑為260 mm、殼程總長1 500 mm、進出口管內徑90 mm、換熱管外徑24 mm、換熱管數量24根，換熱管間距36 mm。 將折流板缺口高度h、折流板數量N和折流板開孔孔徑d作為輸入自變量， 每個因素有3個設計水平，進行正交試驗設計，以換熱器的殼程壓降和表面換熱系數作為目標，進行優化設計。 對管殼式換熱器， 采用三維簡化模型以及CFD進行了模擬計算。 當換熱介質的入口流速為4 m/s時，其正交試驗設計結果列于表1。

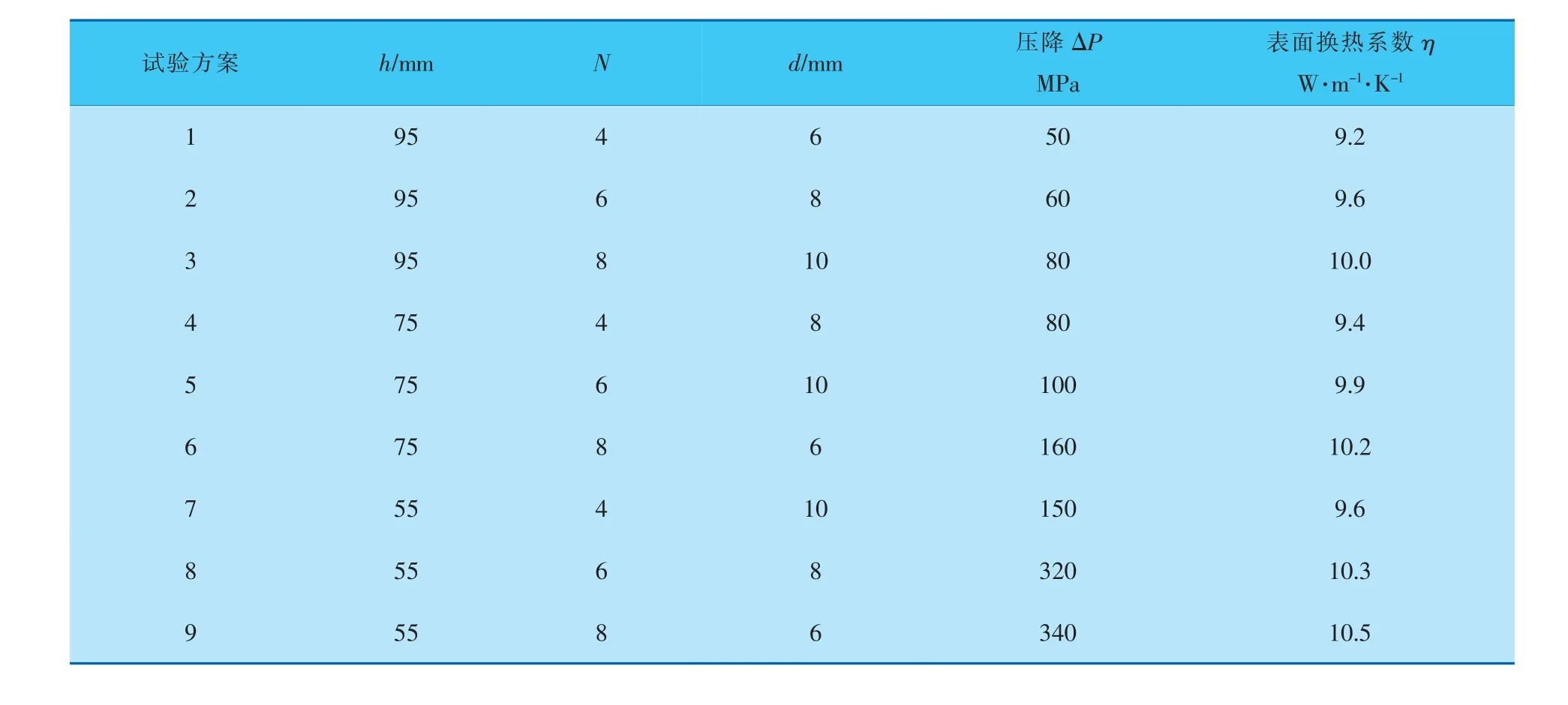
表1 管殼式換熱器多因素正交試驗方案L9（34）及結果

按照概率基多目標優化方法對表1中數據進行處理，得到表2的結果。 其中，壓降△P具有越低越好的特征，屬于成本型指標；表面換熱系數η具有越大越好的特征，屬于效益型指標。 從表2結果可以看出， 方案2具有最大的總青睞概率，因此，優化結果應該在方案2附近。 進一步，對表2給出的總青睞概率進行極差分析， 得到表3的結果。

表2 管殼式換熱器多目標試驗結果的評價情況

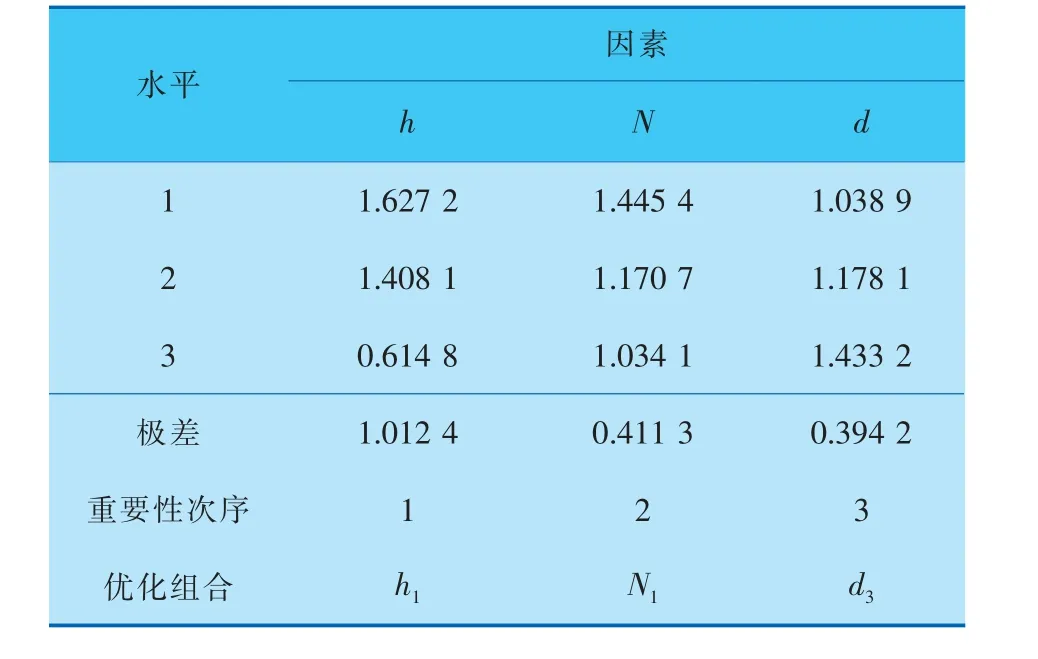
表3 管殼式換熱器概率基多目標評價極差分析

極差分析表明，因素的重要性次序為h＞N＞d。而最終優化的結果為h1N1d3， 即折流板缺口高度h=95 mm、折流板數量N=4塊、折流板開孔孔徑d=10 mm時，換熱器換熱效果可達到最優。 然而，李德濤等采用綜合性能評價因子法，獲得的結果是h=95 mm、折流板數量N=4塊、折流板開孔孔徑d=8 mm［8］，異于本文的結果。

2.2 應用于降黏聚結一體化裝置的優化設計

卜凡熙等針對旋流器處理含聚介質的“消化不良”現象，設計出一種降黏聚結一體化裝置。 將該裝置串聯于聚介質的旋流處理器之前端，在降低聚合物溶液黏度的同時， 還增大了油滴粒徑，從而降低了含聚介質黏度和油滴乳化程度對旋流器分離性能的影響。 同時，為了提高裝置的降黏聚結效果，采用正交試驗方法對其進行了結構尺寸優化。試驗選取A、B、C、D、E、F、G7個因素，每個因素設定3個水平，并以油滴粒徑、黏度和壓降為3個優化目標，進行了優化設計。 采用了三維簡化模型以及CFD進行模擬計算， 其正交設計結果列于表4［9］。

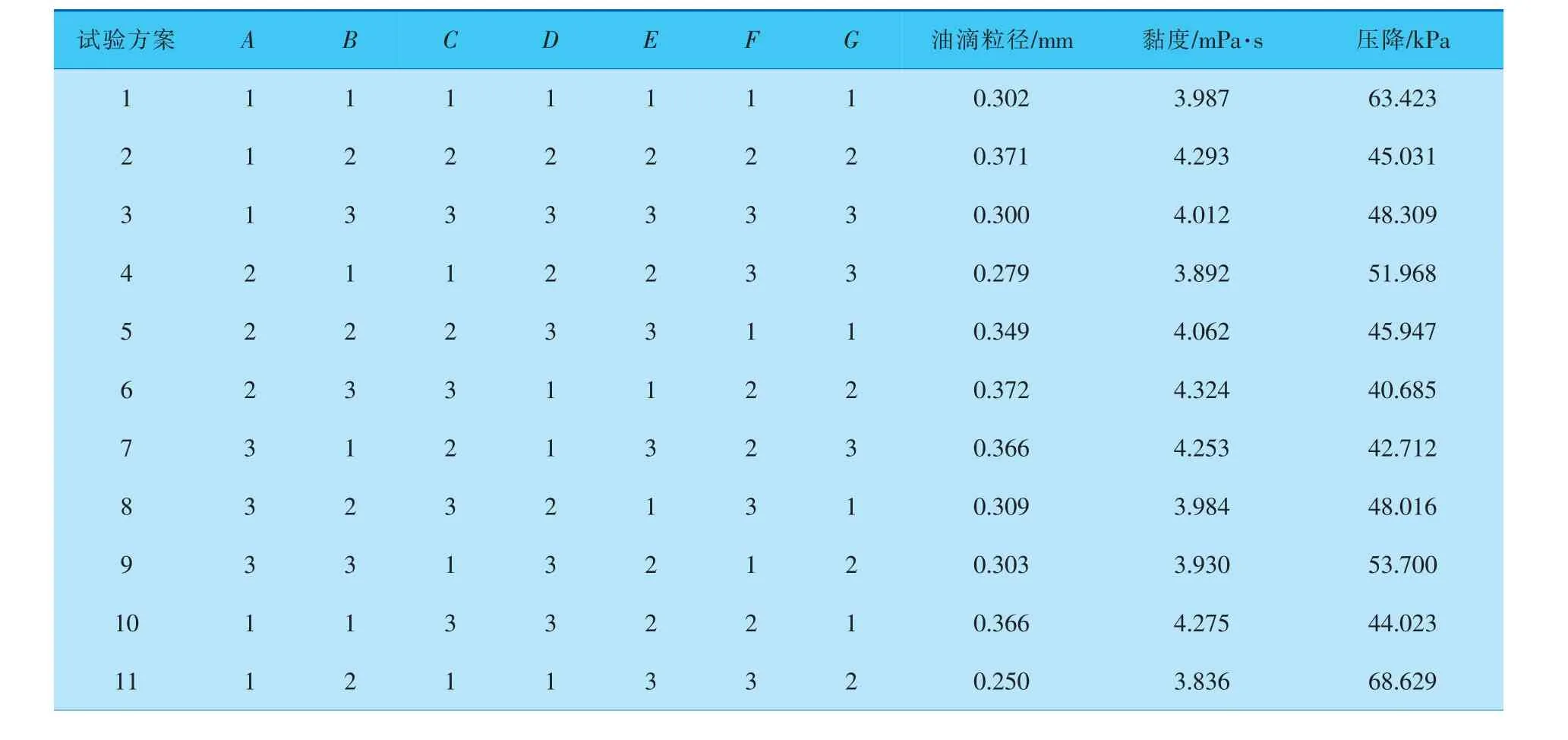
表4 降黏聚結一體化裝置的正交試驗L18（2137）方案及結果

按照概率基多目標優化方法對表4中數據進行處理，得到的結果列于表5，其中，油滴粒徑為效益型指標，黏度和壓降為成本型指標。從表5可以看出， 試驗方案6具有最大的總青睞概率，因此，優化結果應該在方案6附近。 進一步，對表5給出的總青睞概率進行極差分析， 得到表6的結果。

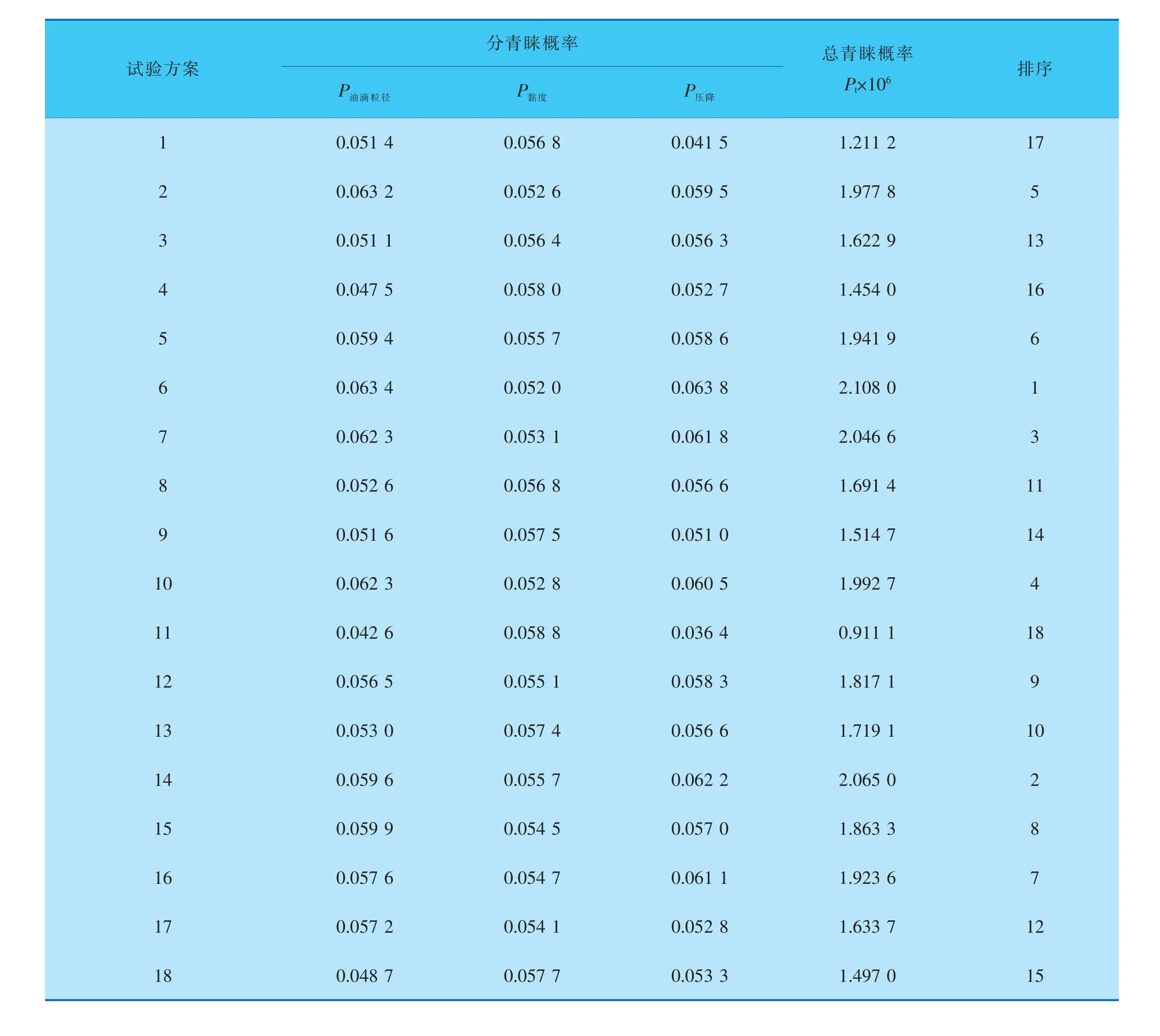
表5 降黏聚結一體化裝置多目標試驗結果的評價情況

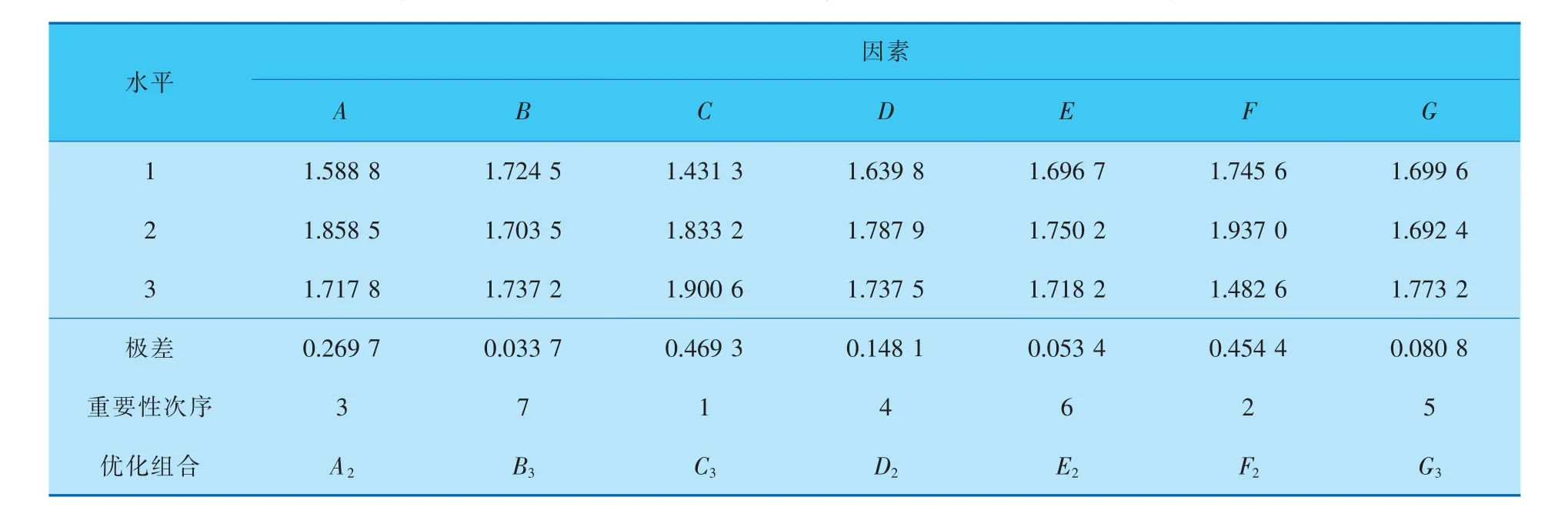
表6 降黏聚結一體化裝置概率基多目標評價極差分析

極差分析結果表明， 因素的重要性次序為C＞F＞A＞D＞G＞E＞B， 最終優化結果為A2B3C3D2E2F2G3時，降黏聚結一體化裝置可達到最優。卜凡熙等采用“綜合平衡法”處理了這一問題［9］，得到的最終優化結果為A2B2C3D2E2F2G1，和本文結果有點差異。

2.3 應用于等距螺旋錐齒輪MIM工藝參數多目標穩健性優化

劉贛華等針對等距螺旋錐齒輪， 利用Moldex3D軟件和正交試驗設計進行了金屬粉末注射成型（MIM）工藝成形的仿真分析。 以體積收縮率和粉末濃度為目標函數，試圖通過對目標函數均值分析和極差的分析，并利用BP神經網絡結合非支配排序遺傳算法（NSGA-Ⅱ）進行MIM工藝參數的優化。 MIM工藝參數優化考慮了5個影響因子，即保壓壓力A、充填時間B、澆口直徑C、熔體溫度D和模具溫度E，每個因子設計了5個水平，并采用L25（55）進行正交試驗設計［10］。 其正交設計結果列于表7。其中，μ和σ分別表示體積收縮率與粉末濃度的平均值和標準差；合金粉末的輸入體積分數為60%。

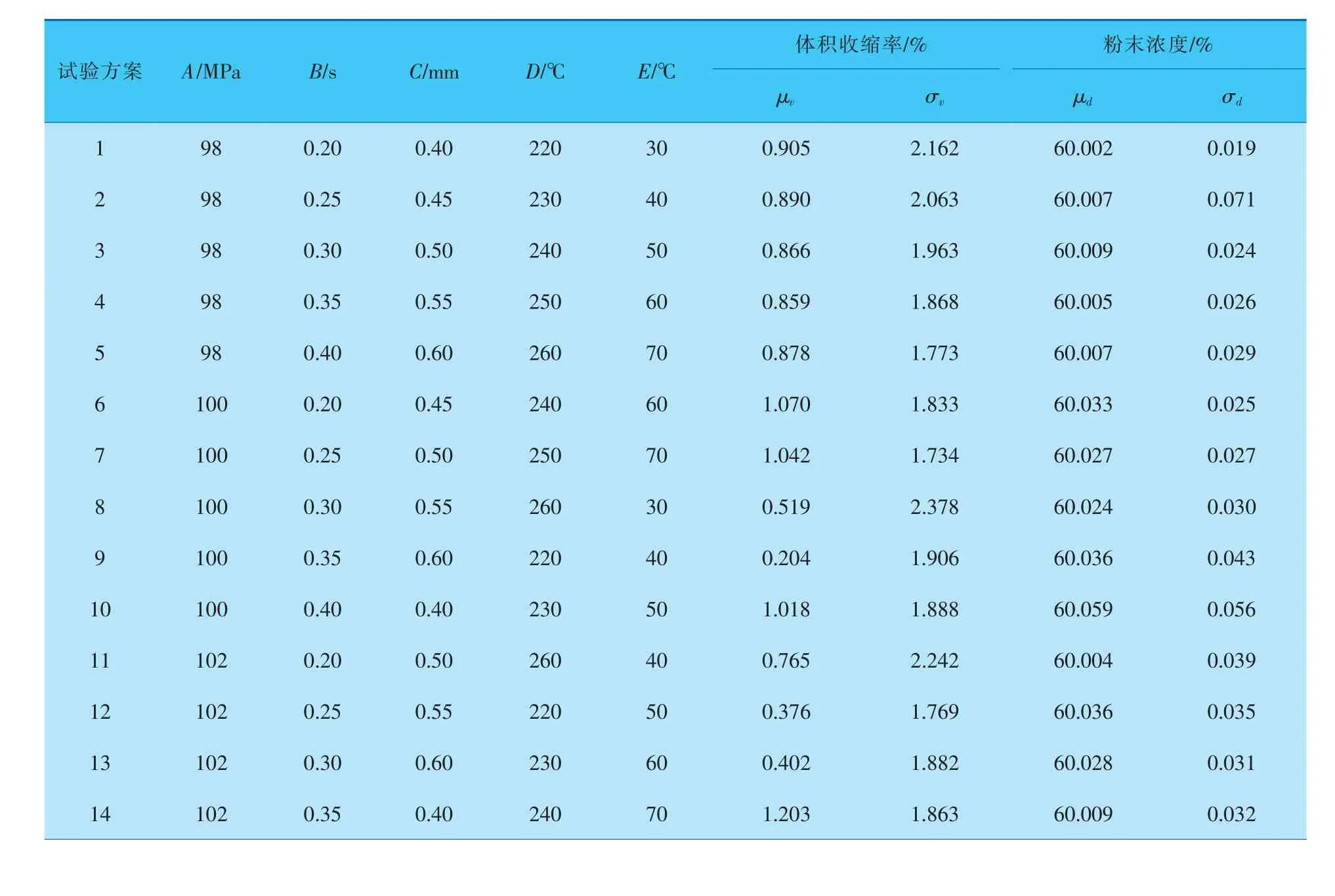
表7 MIM工藝參數的L25（55）正交試驗方案及體積收縮率與粉末濃度結果

筆者針對這一問題，采用概率基多目標穩健性評價［1］，由于粉末濃度的輸入值為60%，故其效用值應為ε=|60%-μv|，具有越小越好的特征；同時體積收縮率的平均值和標準差、粉末濃度的標準差也具有越小越好的特征。按照概率基多目標優化方法的穩健性評價方法，以及粉末濃度的效用值ε的定義，對表7中數據進行處理得到表8的結果。

表8 MIM工藝參數試驗結果的多目標穩健性評價情況

以Pt=（Pμv·Pσv）×（Pμd·Pσd）為依據進行總青睞概率Pt的評估［1］。 由表8可知，試驗方案25（A5B5C4D3E2）具有最大的總青睞概率，因此，優化結果應該在方案25附近。 進行極差分析得到表9結果。

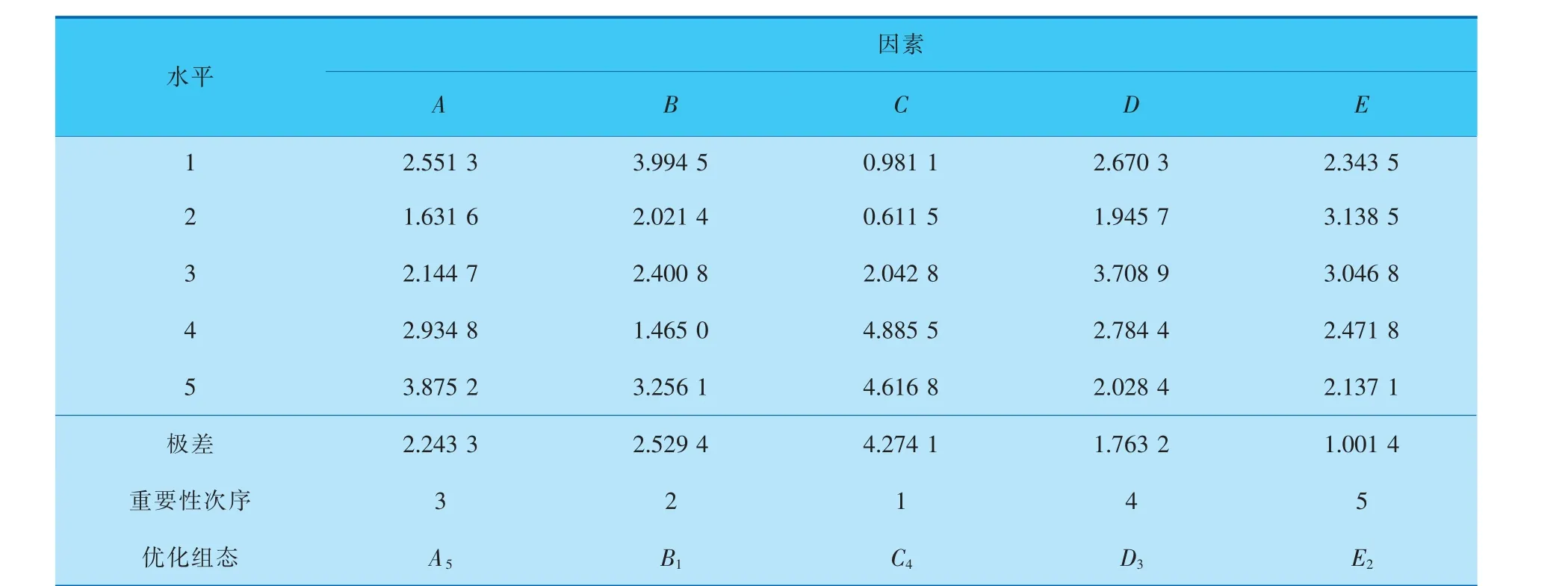
表9 MIM工藝參數試驗結果的概率基多目標評價極差分析

極差分析結果顯示，因素的重要性次序為C＞B＞A＞D＞E，最終優化結果為A5B1C4D3E2，即保壓壓力A=106 MPa、 充填時間B=0.20 s、 澆口直徑C=0.55 mm、熔體溫度D=240 ℃和模具溫度E=40 ℃。劉贛華等采用“BP神經網絡結合非支配排序遺傳算 法（NSGA-Ⅱ）”處 理 了 這 一 問 題［10］，得 到 的Pareto最優解為：保壓壓力A=99.183 MPa、充填時間B=0.241 s、澆口直徑C=0.548 mm、熔體溫度D=240.702 ℃、模具溫度E=63.981 ℃，有異于本文的結果。

上述3個案例的計算結果均與本文結果存在差異，其原因在于概率基多目標優化屬于系統的優化方法，期待之后有學者對計算效果進行驗證評價。

3 結束語

將概率基多目標優化方法和正交試驗設計，以及穩健性設計結合起來，可以得到概率基多目標正交試驗優化設計和穩健性設計方法。 將概率基多目標正交試驗優化設計方法應用于管殼式換熱器折流板結構參數優化的正交試驗設計和降黏聚結一體化裝置的優化設計，概率基多目標穩健性設計方法應用于等距螺旋錐齒輪MIM工藝參數多目標的穩健性設計，得到了多個目標同時優化的結果。 該方法簡便易行，可望在廣泛領域得到應用。