基于模擬退火算法的數控機床熱誤差補償方法
蔡楊,王春飛,錢小勇
(1.浙江永成機械有限公司,浙江 諸暨 311835;2.華北電力大學 能源動力與機械工程學院,北京 102206;3.浙江盾運實業有限公司 生產技術部,浙江 諸暨 311835;4.浙江豪路熱能科技有限公司 生產技術部,浙江 諸暨 311835)
0 引言
數控機床是機械加工的基礎,可以直接決定一個國家的制造業水平。進入21世紀以來,幾乎所有的機械制造技術都向著高精密加工的方向發展,數控機床的加工精度成為了研究者的重點研究對象。在數控機床加工精度誤差中,熱誤差是最大的一個阻礙。為了減小精密加工過程中的熱誤差,研究人員紛紛對數控機床的熱誤差補償方法進行設計。李國龍等[1]使用天鷹優化卷積神經網絡算法,對精密數控機床的熱誤差進行建模分析,在總結了系統的熱變形規律之后,篩選出關鍵的溫度點,并提出優化的卷積核結構,建立了一個熱誤差的預測模型,基于該模型建立的補償機制可以有效地提高補償精度。曹利等[2]使用MEA-BP算法對數控機床的加工主軸進行了優化,總結了溫升條件與熱誤差之間的關系,同時結合實驗,驗證了該方法在不同的工況下均具備較好的補償精度與泛化能力。李有堂等[3]以提高數控機床精度為目標,結合布谷鳥算法,轉化了高維線性問題的求解思路,在最小二乘支持向量機的建模方法下,完成了對最小化線性規劃的分析。該方法具備良好的預測效果,同時可以高效地補償數控機床的熱誤差。綜合上述文獻的研究,為進一步提高數控機床的熱誤差補償精度,本文設計了一種基于模擬退火算法的數控機床熱誤差補償方法。
1 計算高速運動機床發熱量
在多體運動過程中,分別求解平移運動和旋轉運動所對應的齊次坐標變換矩陣。在沿X軸、Y軸、Z軸方向做平移運動時,矩陣P(x)、P(y)和P(z)可以表示為:
該矩陣中,x、y、z均可以表示為平移運動下物體的變化量[4-5]。旋轉運動時的齊次坐標變化矩陣則可以簡化為
式中:XT為物體作旋轉運動時的齊次變化矩陣,αx、αy和αz分別為X軸、Y軸、Z軸下物體的旋轉角度[6-7]。
在數控機床內,通過位姿誤差和運動誤差計算加工機床的幾何誤差,其中的位姿誤差不會跟隨零件運動而發生位置的偏移。在此過程中,電動機與軸承的發熱量為:
式中:Qd為電動機的發熱量;Qz為軸承的發熱量;Pk為電動機內部磁極數量,該磁極一般成對出現;n為電動機主軸的轉動速度,r/min;tm為電動機運行的轉矩;δs為電動機運行功率;Jk為電動機與軸承的摩擦力矩[8]。
將電動機與軸承的發熱量相加,就是高速運動下該數控機床的發熱量。
2 基于模擬退火算法建立熱誤差偏移補償模型
想要獲取最佳的熱誤差補償結果,就需要建立一個熱誤差的補償模型。結合模擬退火算法,在該模型內選擇一個熱平衡狀態,此時系統溫度的狀態參量可以表示為
式中:P(Tm)為該熱平衡狀態下的系統溫度參量,G(Tm)為系統熱平衡轉移情況下的狀態函數,xk為溫度系數[9-10]。
在溫度下降后,得到求和單元的傳遞函數:
式中:Uk和Ud分別為求和單元內模式層及計算層內的加權求和結果,Pi為第i個樣本的輸入值,Fi為連接權值。當模擬退火算法的粒子進入平衡狀態后,可以得到固化后的最低能量晶體,此時的熱誤差偏移補償模型的狀態轉換一般能夠得到大于1的數值,其計算公式為
式中:Gm為熱誤差偏移補償模型在轉換條件下的狀態參量,F(i)為轉移前的狀態函數,F(j)為轉移后的狀態函數,Dk為能量粒子的平衡常數[11-12]。
由此可以得到該偏移補償模型內X軸、Y軸、Z軸上經過多次迭代后的位置:
式中:Dx為X軸方向上數控機床經過熱誤差補償后的位置,Dy和Dz分別為Y軸與Z軸的補償后位置,c1和c2分別為智能體的光滑因子和泛化因子,Xi(t)和Xj(t)分別為補償前X軸的位置與補償變化值,Yi(t)為補償前Y軸的位置,Yj(t)為補償后Y軸變化值,Zi(t)和Zj(t)則分別為補償前Z軸的位置與補償變化值[13-14]。
通過式(9)可以獲得基于模擬退火算法的熱誤差偏移補償模型。
3 設計數控機床熱誤差補償算法
結合上文中針對數控機床的熱誤差偏移補償模型,可以設計一個熱誤差補償算法,該算法的流程如圖1所示。
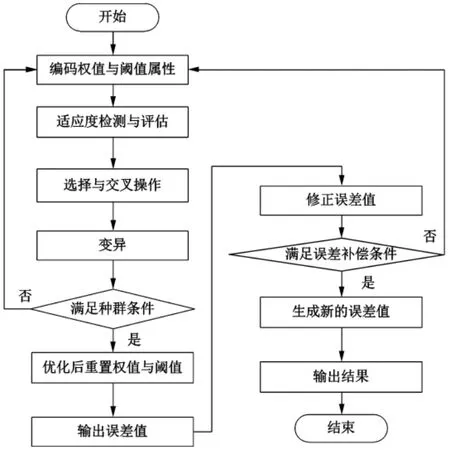
圖1 熱誤差補償算法
如圖1所示,通過權值與閾值的編碼,可以得到一個適應度評價結果,將其與檢測結果進行對比與評估,然后進行選擇與交叉操作。變異后,檢查該誤差補償算法得到的結果是否滿足種群條件,如果不滿足條件,需要重新進行權值與閾值的編碼,但是如果滿足條件,則可以對充值后的權值與閾值進行優化處理。此時可以輸出并修正基礎誤差。判斷是否滿足誤差補償條件,若不能滿足補償的基礎條件,需要重新返回到權值的編碼及閾值重構的環節,繼續優化誤差[15]。當滿足誤差補償條件后,可以繼續生成新的數控機床熱誤差補償值,并將該補償值作為輸出結果。由上述流程內的數控機床熱誤差補償算法可以得到數控機床熱誤差補償結果。
4 實驗研究
4.1 搭建測試平臺
本文設計了一種基于模擬退火算法的數控機床熱誤差補償方法,為測試該方法的實用性及優越性,設計了實驗方案。該實驗使用MIK-R6000F系列的無紙記錄儀作為多通道數據采集儀,該型號的配電輸出為150 mA,內部存在通信接口和USB數據轉存接口,通過USB接口與計算機相連,可以在穩定的環境下收集數控機床的數據。標準球目標的使用規格為25.4 mm,使用高精度的標準球目標并將其固定在軸端的兩側,從而實現熱位移的測量。位移傳感器則使用PZ11系列微型拉桿式位移傳感器,該傳感器的最高運行速度可以達到5 m/s,運行壽命能夠達到1000萬次以上,位移測量精度為0.1%。在搭建熱誤差模型的過程中,依據傳感器的布置原則,以此得到數控機床熱誤差補償測試時所適用的傳感器位置(如圖2)。
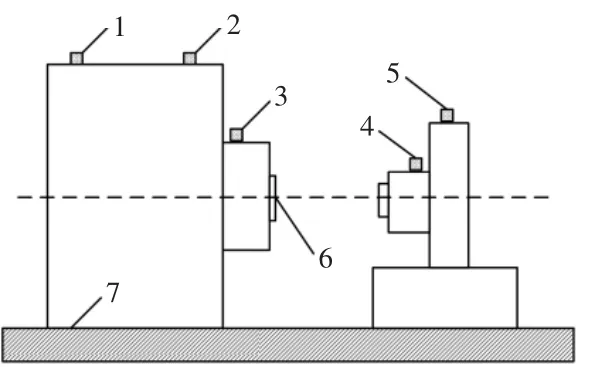
圖2 傳感器位置
如圖2所示,1~4號位置分別為編號為001~004的傳感器,5號位置為數控機床主軸,6號位置為位移傳感器,7號位置為機床的支撐座。
4.2 模型優化結果
收集上述測試平臺中的100組數據,并將其分為2個部分,分別作為測試集和訓練集。其中訓練集為70 組數據,測試集為30組數據。該模型的學習效率為0.01,誤差平方和的指標為0.001,最大迭代次數為160。此時可以得到該模型的適應度曲線和誤差平方和曲線,如圖3所示。
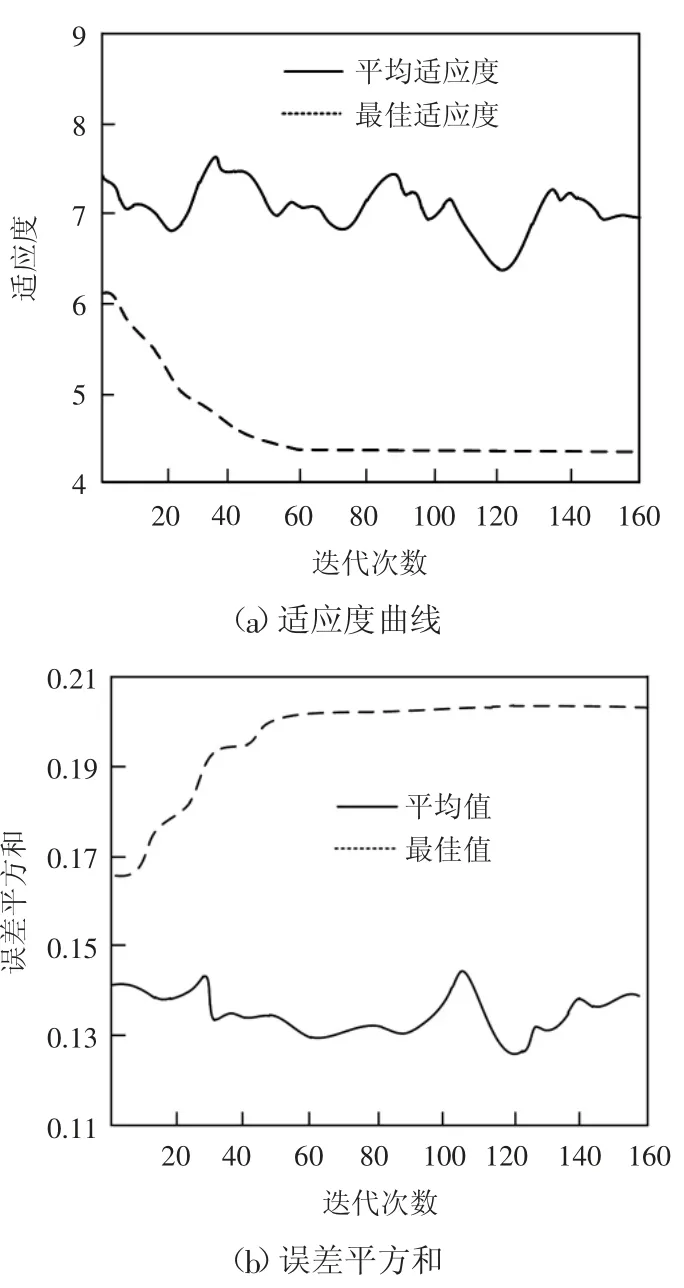
圖3 模型優化結果
在適應度曲線中,最佳適應度在第60次迭代以后趨于平緩,此時的適應度值約為4.5,而平均適應度則在6.5~8之間。在誤差平方和的測試中,最佳值同樣在第60次迭代時變得平緩,此時的誤差平方和約為0.20。誤差平方和的平均值則在0.13~0.15之間。兩種模型的優化結果波動均較小,可見該數控機床熱誤差補償模型的穩定性較強。
4.3 熱誤差補償精度對比
在400 min內分別測試數控機床熱誤差補償在X軸、Y 軸、Z 軸上的熱變形量,以0 mm為標準值,分別記錄3組變形數據隨時間變化的曲線。
如圖4所示,通過溫度傳感器可以得知,該數控機床在軸方向的熱變形量先增加、后減少,呈現一個明顯的先上、后下的坡度。Y軸方向的熱變形量則是基本與標準值相貼近,沒有過多的差距。Z軸方向的熱變形量變化趨勢較為復雜,但是基本處于標準值的下方。根據圖4中的熱變形數據可知,在該數控機床中,X軸與Z軸方向的熱變形最明顯,因此可以據此對2組數據建立熱誤差的補償模型:
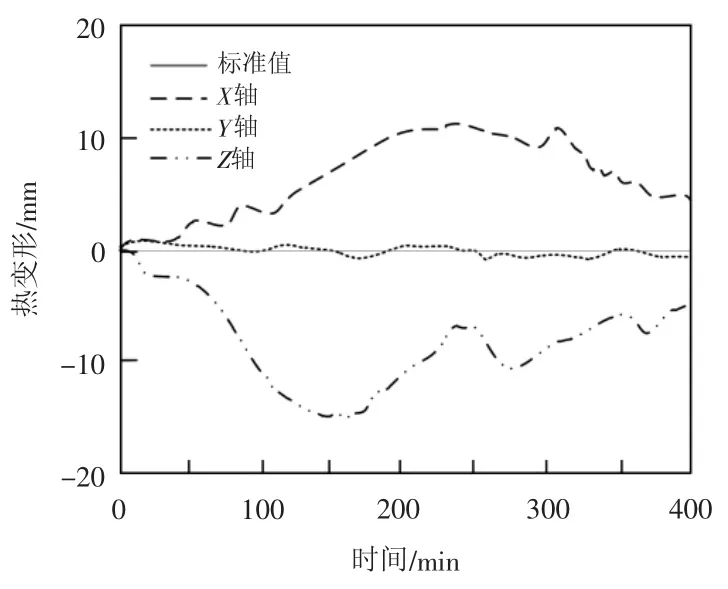
圖4 熱變形數據
式中:ΔX為X軸數據的補償值,ΔZ為Z軸數據的補償值,f1、f2和f3分別為3個軸型對應的模型系數,Tx1和Tx2為X軸上的兩組測點溫度,Tz1和Tz2則分別為Z軸上的測點溫度。
在本實驗中,分別對本文設計的模擬退火算法、天鷹優化卷積神經網絡 算 法 、MEA -BP 算法和優化最小二乘支持向量機方法進行對比測試。通過該補償模型,分別得到4種方法在熱誤差補償前后的實測曲線,如圖5所示。
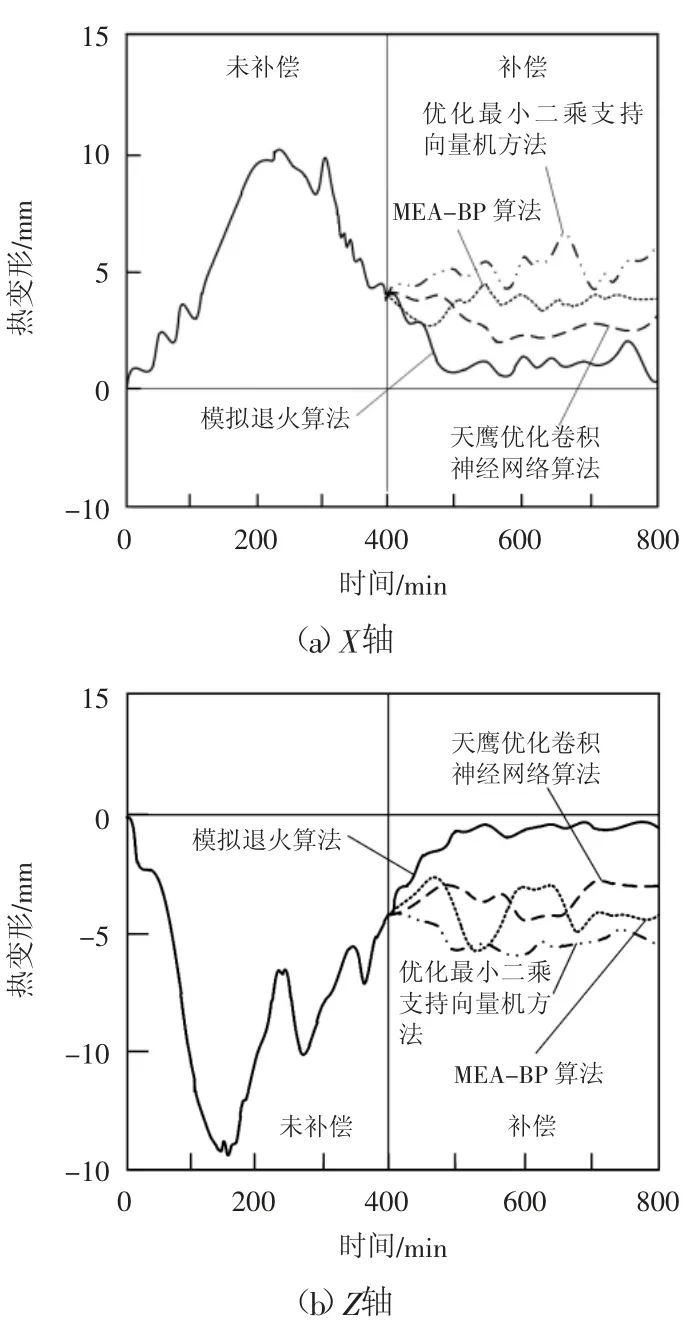
圖5 熱誤差補償前后對比實測曲線
在X軸上,經過熱誤差補償后,4種算法的熱變形量有明顯降低。其中本文設計的模擬退火算法的熱變形量由補償前最大的形變量10 mm降低至補償后的1~2 mm。在熱誤差補償后,天鷹優化卷積神經網絡算法的熱變形量為2~4 mm,MEA-BP算法和優化最小二乘支持向量機方法的熱變形量分別為4~5 mm和4~7 mm。在Z軸上,補償前的變形量最高可以達到14 mm,但是在經過數控機床的熱誤差補償后,模擬退火算法所得到的補償值已經降低至0~1 mm,鷹優化卷積神經網絡算法的熱變形量也降低至2~4 mm,MEA-BP算法和優化最小二乘支持向量機方法的熱變形量分別降低至2~5 mm和4~6 mm。通過上述實驗結果可知,在上述4種數控機床熱誤差補償算法中,本文設計的模擬退火算法得到的熱變形量下降幅度最大,能夠在最大程度上降低數控機床的誤差,保證機床運行的精度。
5 結語
本文設計了一種基于模擬退火算法的數控機床熱誤差補償方法,該方法可以通過建立熱誤差模型,得到相應的補償算法,實驗結果顯示該補償方法的效果極好,比其他3種對比方法的補償精度更好。通過該方法可以得到精度更高的機械加工產品。本文設計的加工機床僅對有熱誤差導致的加工誤差進行了消減,對其他方面的誤差沒有深入的研究。除了熱誤差之外,機床加工的精度還會受到幾何誤差、力致誤差等的影響,因此需要分別對各類誤差進行溯源整理,并進一步提高數控機床的加工精度。

