新的廣義時滯系統(tǒng)容許性條件






摘要:針對廣義時滯系統(tǒng),基于李雅普諾夫第二方法和廣義系統(tǒng)的受限等價變換,結(jié)合積分不等式技術,給出一個線性矩陣不等式(linear matrix inequality,LMI)形式的容許性條件。首先,利用廣義系統(tǒng)的受限等價變換得出廣義時滯系統(tǒng)是正則且無脈沖的;然后,通過選取增廣型LyapunovKrasovskii泛函(LK泛函)和多重積分型LK泛函,引入松弛型LK泛函構建新的LK泛函,利用Jensen積分不等式和Wirtinger積分不等式對LK泛函求導后產(chǎn)生的積分項進行處理,得出廣義時滯系統(tǒng)的穩(wěn)定性條件,進而得到廣義時滯系統(tǒng)的容許性條件;最后,利用MATLAB中的LMI工具箱,通過數(shù)值算例驗證所用方法的可行性和有效性。
關鍵詞:廣義時滯系統(tǒng); 容許性條件; LyapunovKrasovskii泛函; Jensen積分不等式; Wirtinger積分不等式
中圖分類號:O231文獻標志碼:A
doi:10.3969/j.issn.16735862.2024.02.011
CUI Song LYU Yan CHEN Lanfeng SUN Xin, WANG Hanxuan
(1. College of Physical Science and Technology, Shenyang Normal University, Shenyang 110034, China)
(College of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)
Abstract:Based on Lyapunov′s second method and limited equivalent transformations of descriptor systems, combined with the integral inequality technique, an admissibility condition for descriptor delay systems is given in the form of linear matrix inequality (LMI). Firstly, it is concluded that the descriptor delay system is regular and impulse free by using limited equivalent transformations of descriptor systems. Secondly, a new LyapunovKrasovskii functional (LK functional) is constructed by selecting the augmented LK functional, multiple integral LK functional and introducting the relaxed LK functional, and then, the integral terms producted by derivation of LK functional are dealt with by Jensen integral inequality and Wirtinger integral inequality, respectively. Thus, a stability condition for the descriptor delay system is obtained, correspondingly, an admissibility condition for the descriptor delay system is obtained. Finally, a numerical example is provided to demonstrate feasibility and validity of the proposed method by virtue of LMI toolbox of MATLAB.
Key words:descriptor delay systems; admissibility condition; LyapunovKrasovskii functional; Jensen integral inequality; Wirtinger integral inequality
廣義系統(tǒng),又稱奇異系統(tǒng)、微分代數(shù)系統(tǒng)、廣義狀態(tài)空間系統(tǒng)等[1]。與正常系統(tǒng)相比,廣義系統(tǒng)的形式更加一般,可以更精準地描述一些物理現(xiàn)象,其在許多實際系統(tǒng)中,如電力系統(tǒng)、航空航天系統(tǒng)、社會經(jīng)濟系統(tǒng)中得到了廣泛應用。近年來,學者們對于廣義系統(tǒng)的研究主要集中在穩(wěn)定性分析方面[23]。時滯是工程實際中普遍存在的現(xiàn)象,信息或物質(zhì)的傳遞都會產(chǎn)生時滯,如流體的傳輸、電力的輸送等,但時滯的存在往往會降低系統(tǒng)的性能,甚至使系統(tǒng)變得不穩(wěn)定。因此,研究廣義時滯系統(tǒng)具有重要的理論意義和實用價值。目前,對廣義時滯系統(tǒng)的研究已經(jīng)非常深入,如指數(shù)穩(wěn)定性[4]、魯棒穩(wěn)定性[5]、H∞濾波[6]、滑模控制[7]等。
對廣義時滯系統(tǒng)的研究既要考慮廣義系統(tǒng)的正則性和無脈沖性,又要考慮時滯對系統(tǒng)穩(wěn)定性的影響,難度更大,更具有挑戰(zhàn)性。針對廣義時滯系統(tǒng)容許性問題,為了降低容許性條件的保守性,常采用以下2種方式:1)構造合適的LK泛函,充分利用系統(tǒng)本身的狀態(tài)信息和時滯信息;2)選取合適的積分不等式處理LK泛函求導后產(chǎn)生的積分項,將容許性條件寫成線性矩陣不等式(linear matrix inequality,LMI)形式,便于利用MATLAB求解。構造LK泛函時通常采用簡單型[8]、多重積分型[910]、增廣型[11]、松弛型[1214]等形式。常用的積分不等式主要有Jensen積分不等式、Wirtinger積分不等式、輔助函數(shù)積分不等式等。
1問題描述
2主要結(jié)果
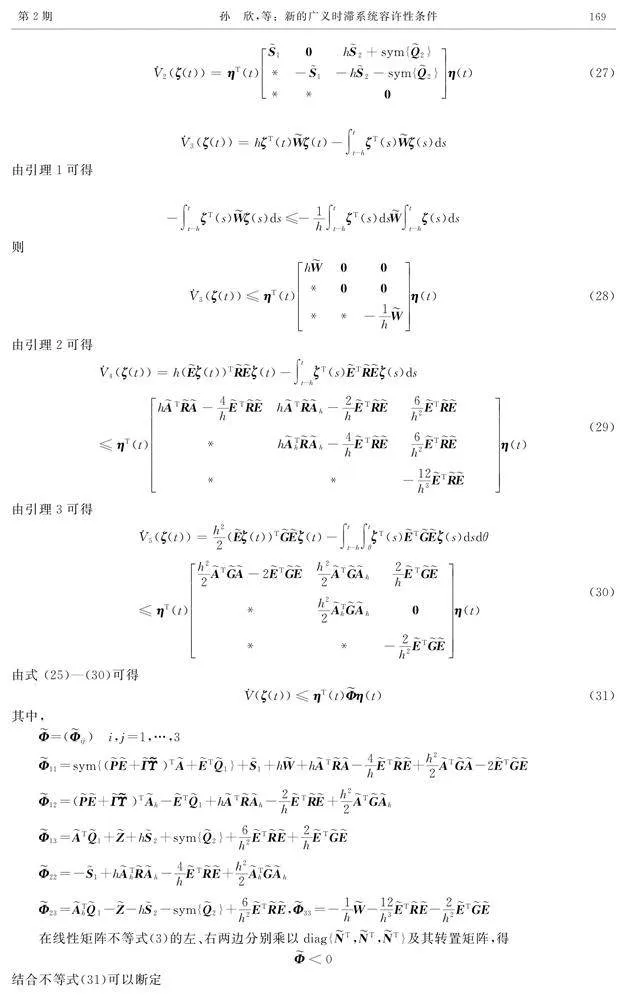
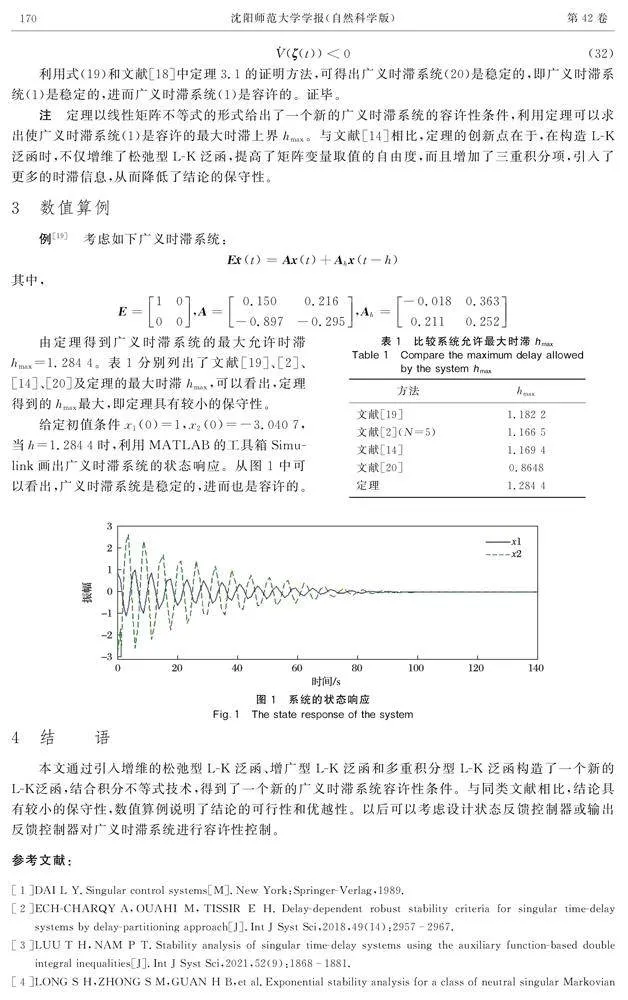
3數(shù)值算例
4結(jié)語
本文通過引入增維的松弛型LK泛函、增廣型LK泛函和多重積分型LK泛函構造了一個新的LK泛函,結(jié)合積分不等式技術,得到了一個新的廣義時滯系統(tǒng)容許性條件。與同類文獻相比,結(jié)論具有較小的保守性,數(shù)值算例說明了結(jié)論的可行性和優(yōu)越性。以后可以考慮設計狀態(tài)反饋控制器或輸出反饋控制器對廣義時滯系統(tǒng)進行容許性控制。
參考文獻:
[1]DAI L Y.Singular control systems[M].New York:SpringerVerlag,1989.
[2]ECHCHARQY A,OUAHI M,TISSIR E H.Delaydependent robust stability criteria for singular timedelay systems by delaypartitioning approach[J].Int J Syst Sci,2018,49(14):29572967.
[3]LUU T H,NAM P T.Stability analysis of singular timedelay systems using the auxiliary functionbased double integral inequalities[J].Int J Syst Sci,2021,52(9):18681881.
[4]LONG S H,ZHONG S M,GUAN H B,et al.Exponential stability analysis for a class of neutral singular Markovian jump systems with timevarying delays[J].J Franklin I,2019,356(12):60156040.
[5]YANG X Y,LI X D,CAO J D.Robust finitetime stability of singular nonlinear systems with interval timevarying delay[J].J Franklin I,2018,355(3):12411258.
[6]ZHOU J,LV Y W,PANG B,et al.H∞ filtering for a class of singular timedelay systems[J].Int J Control Autom,2019,17(12):31313139.
[7]ZHANG Y,ZHANG Q L,ZHANG J Y,et al.Slidingmode control for fuzzy singular systems with timedelay based on vector integral sliding mode surface[J].IEEE T Fuzzy Syst,2020,28(4):768782.
[8]RICHARD J P.Timedelay systems:An overview of some recent advances and open problems[J].Automatica,2003,39(10):16671694.
[9]WANG J D,WANG Z S,DING S B,et al.Refined Jensenbased multiple integral inequality and its application to stability of timedelay systems[J].IEEECAA J Automatic,2018,5(3):758764.
[10]CHEN J,PARK J H,XU S Y.Stability analysis for neural networks with timevarying delay via improved techniques[J].IEEE T Cybernetics,2019,49(12):44954500.
[11]SEURET A,GOUAISBAUT F.Wirtingerbased integral inequality:Application to timedelay systems[J].Automatica,2013,49(9):28602866.
[12]XU S Y,LAM J,ZHANG B Y,et al.New insight into delaydependent stability of timedelay systems[J].Int J Robust Nonlin,2015,25(7):961970.
[13]XU S Y,LAM J,ZHANG B Y,et al.A new result on the delaydependent stability of discrete systems with timevarying delays[J].Int J Robust Nonlin,2014,24(16):25122521.
[14]LIU G B.New results on stability analysis of singular timedelay systems[J].Int J Syst Sci,2017,48(7):13951403.
[15]XU S Y,VAN DOOREN P,STEFAN R,et al.Robust stability and stabilization for singular systems with state delay and parameter uncertainty[J].IEEE T Automat Contr,2002,47(7):11221128.
[16]GU K Q.A further refinement of discretized Lyapunov functional method for the stability of timedelay systems[J].Int J Control,2001,74(10):967976.
[17]SUN J,LIU G P,CHEN J.Delaydependent stability and stabilization of neutral timedelay systems[J].Int J Robust Nonlin,2009,19(12):13641375.
[18]SUN X,ZHANG Q L.Delaydependent robust stabilization for a class of uncertain singular delay systems[J].Int J Innov Comput I,2009,5(5):12311242.
[19]ZHI Y L,HE S P,ZHANG Z M.Further improvement for admissibility analysis of singular timedelay systems[J].IEEE T Syst Man CyS,2022,52(8):48074812.
[20]XU S Y,LAM J,ZOU Y.An improved characterization of bounded realness for singular delay systems and its applications[J].Int J Robust Nonlin,2008,18(3):263277.
【責任編輯:溫學兵】

