68Ni和132Sn中同位旋矢量的巨偶極共振

摘要：探討了豐中子原子核68Ni和雙幻核132Sn中的同位旋矢量巨偶極共振現象。采用SkyrmeHartreeFock+BardeenCooperSchrieffer（SkyrmeHF+BCS）方法，計算了核的基態性質；通過無規相位近似法（random phase approximation， RPA）詳細研究了偶極激發態的性質；應用非相對論參數計算了68Ni和132Sn的響應方程分布，并特別分析了對關聯效應對響應方程分布的影響。在這項研究中，不僅觀察到了巨偶極共振（giant dipole resonance， GDR），還在低于11.7 MeV的能量區域內發現了矮偶極共振（pygmy dipole resonance， PDR）。此外，研究發現響應方程中的矮偶極共振對于對稱能密度的敏感性非常顯著，因此可以用來約束對稱能密度的行為。在選擇非相對論參數時，保持了除對稱能以外的所有有效參數不變，這有助于排除其他因素的影響，從而更準確地限制對稱能密度的行為。因此，研究結果有望為進一步理解對稱能密度依賴行為提供有力的數據支持。

關鍵詞：巨偶極共振; 矮偶極共振; 無規相位近似; 響應方程; 對關聯

中圖分類號：O469文獻標志碼：A

doi：10.3969/j.issn.16735862.2024.02.012

CUI Song LYU Yan CHEN Lanfeng LIU Ling LU Yuwei CAO Ligang

（1. College of Physical Science and Technology， Shenyang Normal University， Shenyang 110034， China）

（1. College of Physics Science and Technology， Shenyang Normal University， Shenyang 110034， China;

2. College of Nuclear Science and Technology， Beijing Normal University， Beijing 100875， China）

Abstract：This research explores in detail the phenomenon of isospin vector giant dipole resonance in neutronrich nuclei 68Ni and the doublemagic nucleus 132Sn. We use the SkyrmeHartreeFock+BardeenCooperSchrieffer （SkyrmeHF+BCS） method to calculate the ground state properties of the nucleus. The properties of dipole excited states were studied in detail using the random phase approximation （RPA） method. We applied non relativistic parameters to calculate the response equation distribution of 68Ni and 132Sn， and particularly analyzed the impact of correlation effects on the response equation distribution. In this study， we not only observed giant dipole resonance （GDR）， but also found pygmy dipole resonance （PDR） in the energy region below 11.7 MeV. In addition， research has found that the sensitivity of short dipole resonance in the response equation to symmetric energy density is very significant， so it can be used to constrain the behavior of symmetric energy density. When selecting non relativistic parameters， this study maintained all effective parameters except for symmetric energy unchanged， which helps to exclude the influence of other factors and more accurately limit the behavior of symmetric energy density. Therefore， our research results are expected to provide strong data support for further understanding the symmetric energy density dependent behavior.

Key words："giant dipole resonance; pygmy dipole resonance; random phase approximation; response equation; bardeen cooper schrieffer

巨偶極共振最早在光核反應中被發現。1947年，鮑爾溫和克拉伯在高能光子入射原子核的實驗中，發現反應截面呈急劇增強的趨勢［1］。隨后的研究揭示，在15～20 MeV的能區內，反應截面顯著上升，同時靶核對入射光子表現出明顯的吸收特征。這一現象被解釋為由原子核的集體運動引起的，即光子激發導致了巨偶極共振。自從20世紀40年代首次發現同位旋矢量巨偶極共振作為最早的巨共振模式以來，人們對其進行了廣泛的理論和實驗研究［24］。1975年，Berman和Fultz對巨偶極共振進行了系統的研究［5］。多年來，對巨共振的研究已經取得了顯著的進展，形成了清晰的理論框架和較為成熟的研究方法［6］。

目前，巨共振的研究逐漸擴展到不穩定核，在豐中子核的低能區域發現了一種新的偶極激發，被稱為矮共振［79］。矮共振的出現與富余中子的躍遷密切相關，它被解釋為過剩中子對質子中子飽和核的振動。不穩定核中矮偶極共振的存在對于解釋天體物理中的元素合成、元素豐度、中子星演化等問題具有重要意義［10］。此外，矮共振的研究也有助于深入了解核物質的狀態方程［1112］。

核物質狀態方程是指核子的能量與核物質密度、溫度以及同位旋不對稱度之間的熱力學關系。核狀態方程一直是核物理和天體物理領域的重要課題，因為它的信息對于研究原子核結構、核碰撞、中子星的結構以及并合過程等都具有關鍵性意義。核物質的不可壓縮性系數Kint是核狀態方程的一個主要物理量，反映了核物質壓縮的難易程度。由于不可壓縮性系數無法直接通過實驗測量，因此其具體數值尚不清楚，只能確定其大致范圍在240±20MeV［13］。

本文的研究重點在于探討豐中子核68Ni和雙幻核132Sn中的同位旋矢量巨偶極共振。選用了不同的Skyrme參數集合，包括非相對論參數SA27n～SA35n、asy26～asy40、s4026～s4040和s5028～s5040。每組參數都關聯一個核不可壓縮性Kint值，處于240±20MeV的范圍內。通過采用SkyrmeHF+BCS近似方法來計算基態性質，以及利用無規相位近似法研究偶極激發態的性質。響應方程是理解這些激發現象的關鍵工具之一，用于描述核系統對外部激勵（如入射光子或中子）的響應。在核物理中，響應方程可用于描述核子系統的激發模式和動力學行為，包括不同能級上的激發態，這些方程構成了理論模型的核心，用于解釋實驗結果。我們詳細研究了豐中子核和雙幻核中偶極激發現象，計算了不同組Skyrme參數下68Ni和132Sn的響應方程圖像，并分析了關聯效應對響應方程分布的影響。

1理論框架

在平均場理論中，每個核子都在其他核子的平均場作用下運動。而一系列核子組成的原子核是費米子系統，質量數為A的原子核體系的歸一化函數Φ可以用單粒子正交歸一化波函數φ的Slater行列式表示為

根據能量最低原理，體系總是要往能量最低的狀態演變，同類核子進行配對之后，出現質量虧損，放出能量，體系總能量降低，體系更加穩定，可能出現配對現象，即對關聯。體系放出的能量即為對能。由于HF理論的平均靜態勢中不包含對相互作用，為了解釋原子核的對關聯效應就需要引入對力勢。把由BCS模型描述的對力效應非耦地加入HF平均場的理論稱為HFBCS理論［14］。我們使用delta函數型對力，它的形式為

2結果與討論

2.1Skyrme相互作用參數

對于SA27n～SA35n這些參數對應的Skyrme相互作用，在擬合相互作用時保持核物質飽和點處的性質不變，不可壓縮性系數均為245MeV。這有助于排除其他因素的影響，得到飽和點處對稱能不同的密度依賴行為。采用這些參數去計算矮共振的能量權重的求和規則與對稱能的斜率呈線性關系。非相對論參數SA27n～SA35n的數據見表1。

2.2不考慮對關聯下68Ni和132Sn的響應方程

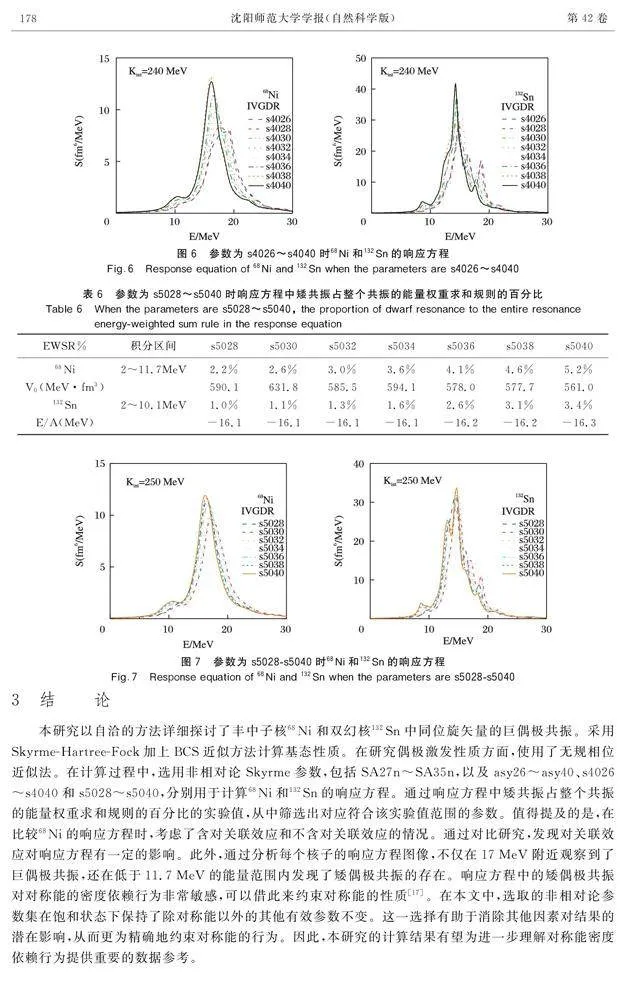
利用SkyrmeHartreeFock方法計算基態性質，對應的基態每核子結合能結果見表2，并利用無規相位近似法研究激發態的性質。使用表1中非相對論參數SA27n～SA35n計算68Ni和132Sn不包含對關聯的響應方程分布，如圖1所示。由圖1可以看到，除了在17MeV附近觀察到巨偶極共振之外，在能量低于11.7MeV的區域中還發現了矮偶極共振，并且隨著參數的不同，對應的響應方程圖像也發生變化，響應方程中矮偶極共振占整個共振的能量權重求和規則（energyweighted sum rule， EWSR）的百分比見表2。

2.3考慮對關聯下68Ni的響應方程

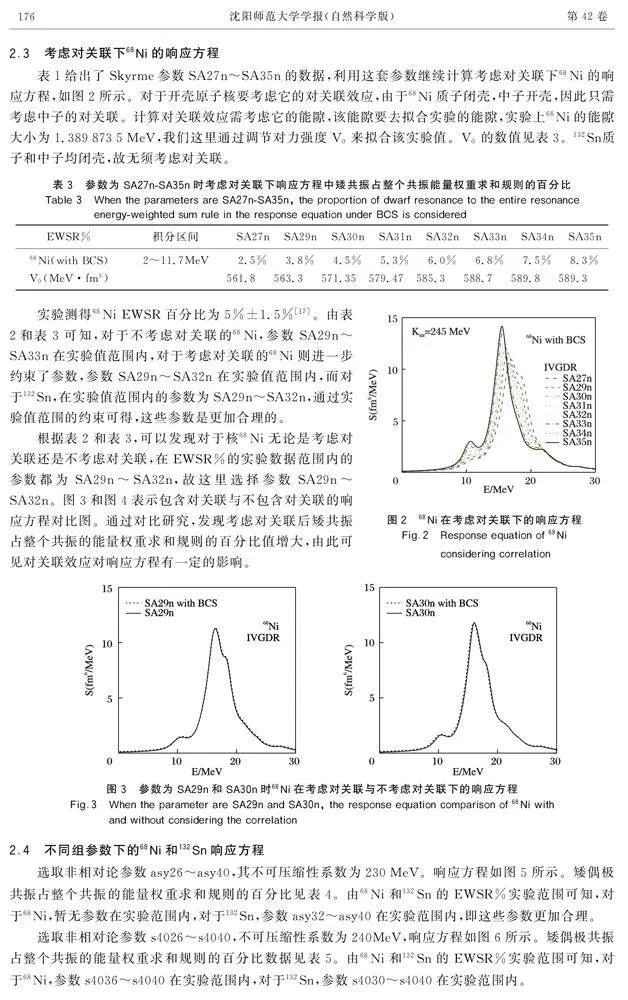
表1給出了Skyrme參數SA27n～SA35n的數據，利用這套參數繼續計算考慮對關聯下68Ni的響應方程，如圖2所示。對于開殼原子核要考慮它的對關聯效應，由于68Ni質子閉殼，中子開殼，因此只需考慮中子的對關聯。計算對關聯效應需考慮它的能隙，該能隙要去擬合實驗的能隙，實驗上68Ni的能隙大小為1.3898735MeV，我們這里通過調節對力強度V0來擬合該實驗值。V0的數值見表3。132Sn質子和中子均閉殼，故無須考慮對關聯。

實驗測得68Ni EWSR百分比為5%±1.5%［17］。由表2和表3可知，對于不考慮對關聯的68Ni，參數SA29n～SA33n在實驗值范圍內，對于考慮對關聯的68Ni則進一步約束了參數，參數SA29n～SA32n在實驗值范圍內，而對于132Sn，在實驗值范圍內的參數為SA29n～SA32n，通過實驗值范圍的約束可得，這些參數是更加合理的。

根據表2和表3，可以發現對于核68Ni無論是考慮對關聯還是不考慮對關聯，在EWSR%的實驗數據范圍內的參數都為SA29n～SA32n，故這里選擇參數SA29n～SA32n。圖3和圖4表示包含對關聯與不包含對關聯的響應方程對比圖。通過對比研究，發現考慮對關聯后矮共振占整個共振的能量權重求和規則的百分比值增大，由此可見對關聯效應對響應方程有一定的影響。

2.4不同組參數下的68Ni和132Sn響應方程

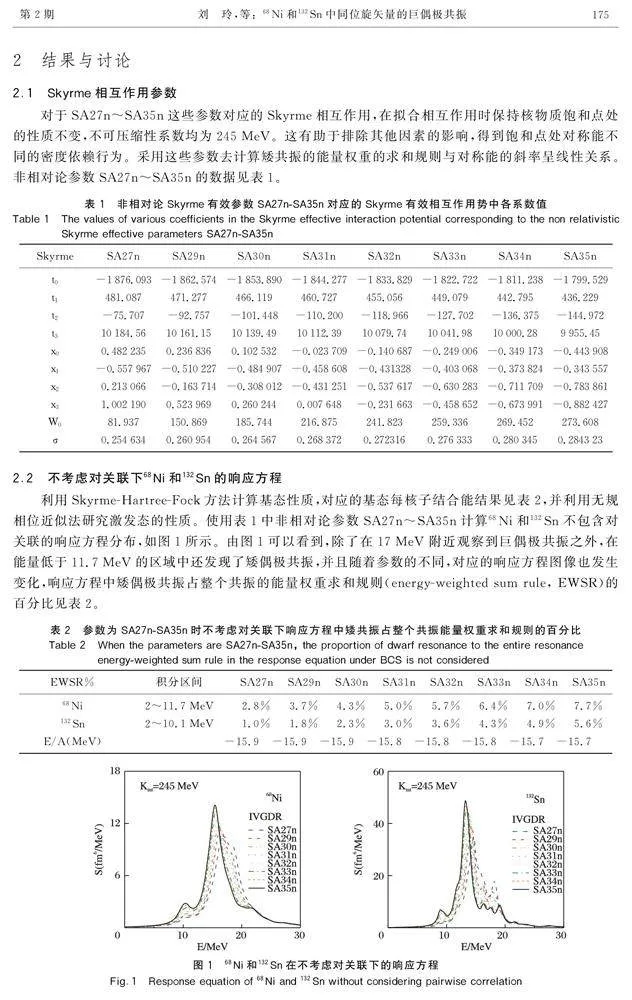
選取非相對論參數asy26～asy40，其不可壓縮性系數為230MeV。響應方程如圖5所示。矮偶極共振占整個共振的能量權重求和規則的百分比見表4。由68Ni和132Sn的EWSR%實驗范圍可知，對于68Ni，暫無參數在實驗范圍內，對于132Sn，參數asy32～asy40在實驗范圍內，即這些參數更加合理。

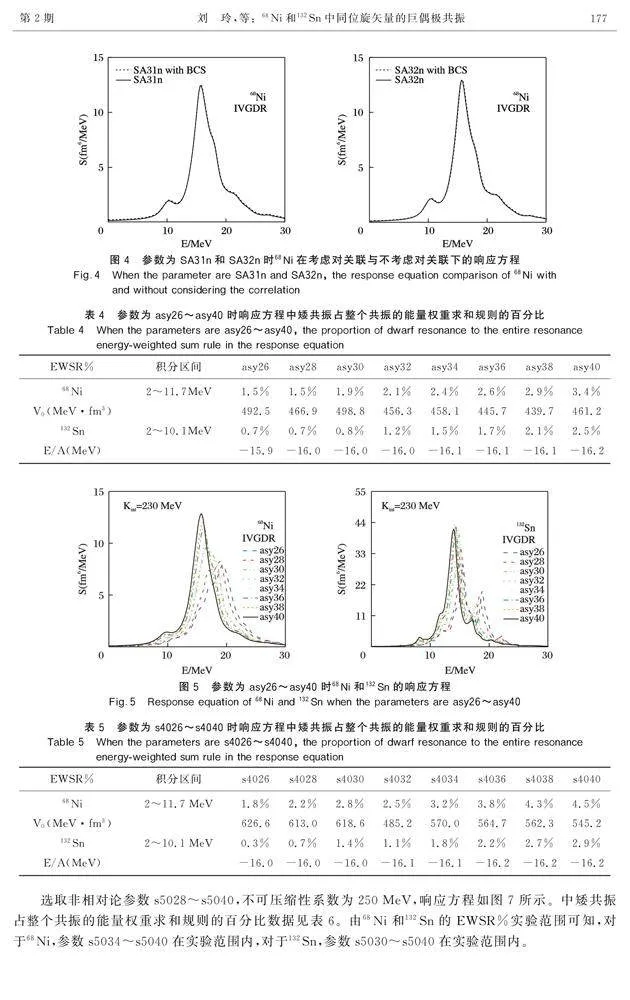
選取非相對論參數s4026～s4040，不可壓縮性系數為240MeV，響應方程如圖6所示。矮偶極共振占整個共振的能量權重求和規則的百分比數據見表5。由68Ni和132Sn的EWSR%實驗范圍可知，對于68Ni，參數s4036～s4040在實驗范圍內，對于132Sn，參數s4030～s4040在實驗范圍內。

3結論

本研究以自洽的方法詳細探討了豐中子核68Ni和雙幻核132Sn中同位旋矢量的巨偶極共振。采用SkyrmeHartreeFock加上BCS近似方法計算基態性質。在研究偶極激發性質方面，使用了無規相位近似法。在計算過程中，選用非相對論Skyrme參數，包括SA27n～SA35n，以及asy26～asy40、s4026～s4040和s5028～s5040，分別用于計算68Ni和132Sn的響應方程。通過響應方程中矮共振占整個共振的能量權重求和規則的百分比的實驗值，從中篩選出對應符合該實驗值范圍的參數。值得提及的是，在比較68Ni的響應方程時，考慮了含對關聯效應和不含對關聯效應的情況。通過對比研究，發現對關聯效應對響應方程有一定的影響。此外，通過分析每個核子的響應方程圖像，不僅在17MeV附近觀察到了巨偶極共振，還在低于11.7MeV的能量范圍內發現了矮偶極共振的存在。響應方程中的矮偶極共振對對稱能的密度依賴行為非常敏感，可以借此來約束對稱能的性質［17］。在本文中，選取的非相對論參數集在飽和狀態下保持了除對稱能以外的其他有效參數不變。這一選擇有助于消除其他因素對結果的潛在影響，從而更為精確地約束對稱能的行為。因此，本研究的計算結果有望為進一步理解對稱能密度依賴行為提供重要的數據參考。

參考文獻：

［1］BALDWIN G C，KLAIBER G S.Xray yield curves for γn reactions［J］.Phys Rev，1948，73（10）：11561163.

［2］ENDERS J，HARTMANN T，MOHR P，et al.Measurement of the dipole and electric quadrupole strength distributions up to 10 MeV in the doubly magic nuclei 40Ca and 48Ca［J］.Phys Rev Lett，2000，85：274277.

［3］ADRICH P，KLIMKIEWICZ A，FALLOT M，et al.Evidence for pygmy and giant dipole resonances in 130Sn and 132Sn［J］.Phys Rev Lett，2005，95：132501.

［4］RUSEV G，SCHWENGNER R，DNAU F，et al.Lowenergy tail of the giant dipole resonance in 98Mo and 100Mo deduced from photonscattering experiments［J］.Phys Rev C，2008，77：064321.

［5］BERMAN B L，FULTZ S C.Measurements of the giant dipole resonance with monoenergetic photons［J］.Rev Mod Phys，1975，47（3）：713761.

［6］HARAKEH M.Giant resonance research：Present interests and future perspectives［J］.Nucl Phys A，2003，731：411417.

［7］GIBELIN J，BEAUMEL D，MOTOBAYASHI T，et al.Decay pattern of pygmy states observed in neutronrich 26Ne［J］.Phys Rev Lett，2008，18（10）：20502055.

［8］PAAR N，NIU Y F，VRETENAR D，et al.Isoscalar and isovector splitting of pygmy dipole structures［J］.Phys Rev Lett，2009，103（3）：032502.

［9］LEHER B，SAVRAN D，AUMANN T，et al.The decay pattern of the pygmy dipole resonance of 140Ce［J］.Phys Lett B，2016，756：7276.

［10］GORIELY S.Radiative neutron captures by neutronrich nuclei and the rprocess nucleosynthesis［J］.Phys Lett B，1998，436（12）：1018.

［11］KLIMKIEWICZ A，PAAR N，ADRICH P，et al.Nuclear symmetry energy and neutron skins derived from pygmy dipole resonances［J］.Phys Rev C，2007，76（5）：051603.

［12］SCHACK M，MISHEV S，PONOMAREV V Y，et al.Investigating the pygmy dipole resonance using beta decay［J］.Phys Rev Lett，2016，116：132501.

［13］BARDEEN J，COOPER L N，SCHRIEFFER J R.Theory of superconductivity［J］.Phys Rev，1957，108（5）：11751204.

［14］CHABANAT E，BONCHE P，HAENSEL P，et al.A Skyrme parametrization from subnuclear to neutron star densities.Part II：Nuclei far from stabilities［J］.Nucl Phys A，1997，635（1-2）：231256.

［15］LASSERRE T.The LENS project：Low energy neutrino spectroscopy［J］.Prog Part Nucl Phys，2002，48（1）：231232.

［16］RING P.Relativistic mean field theory in finite nuclei［J］.Prog Part Nucl Phys，1996，37：193263.

［17］CARBONE A，COLG，BRACCO A，et al.Constraints on the symmetry energy and neutron skins from pygmy resonances in 68Ni and 132Sn［J］.Phys Rev C，2010，81：041301.

【責任編輯：封文江】