延遲回聲狀態神經網絡用于復雜系統分析和應用

摘要：提出一種改進的回聲狀態神經網絡模型，用于復雜系統的長期行為分析和預測，模型通過引入隱層狀態的延遲反饋體現系統過去時刻的信息對當前狀態的影響，避免了傳統回聲狀態網絡方法記憶能力弱的缺點以及獲得最優參數的困難，

關鍵詞：回聲狀態網絡；混沌時間序列；儲備池計算；穩定性；長期預測

中圖分類號：0193文獻標志碼：A文章編號：1671-5489（2024）05-1017-05

Delayed Echo State Neural Network for Analysisand Application of Complex Systems

XU Yichen1，Eric Li2-3

（1.School of Information，Renmin University of China，Beijing 100872，China

2.School of Computing，Engineeringamp;DigitalTechnologies，TeessideUninversityMiddlesbrough TS1 4，North Yorkshire，United Kingdom

3.College of Mathematics，JilinUniversity，Changchun 130012，China）

Abstract：We proposed an improved echo state neural network model for the analysis and prediction of long-term behavior of complex systems.The model introduced the delayed feedback of hidden layer state to reflect the influence of the past time information on the current state of the system，avoiding the shortcomings of weak memory ability and difficulty of obtaining optimal parameters in traditional echo state network methods.

Keywords：echo state network;chaotic time series;reservoircomputing;stability;long-term prediction

回聲狀態網絡（ESN）是一種新型的回歸人工神經網絡（RNN）模型，由于其在復雜動態系統預測問題上性能優異，因此在科學和工程領域已引起廣泛關注[4]，ESN的核心思想是先通過使用儲備池（reservoir）將訓練數據投影到高維特征空間中，然后通過讀出權重將高維狀態映射到輸出數據，讀出權重可通過線性嶺回歸算法計算，克服了使用梯度下降算法帶來的梯度爆炸和梯度消失的困難[5-12]但現有的ESN模型所體現的系統特征隨著時間的推移逐漸消失，在當前時間附近的輸入特征顯著，而對于遠離當前時間的輸入特征太弱而無法回憶，ESN模型這種重視短期行為導致記憶能力不足的特點限制了其解決復雜系統長期預測問題的能力.基于此，本文提出一種具有延遲反饋的回聲狀態網絡模型（delay-ESN），通過考慮儲備層中神經元的延遲效應，引入隱層狀態的延遲反饋體現系統過去時刻信息對當前狀態的影響，從而提高系統的記憶性能.

1回聲狀態網絡

回聲狀態網絡是一種特殊的回歸神經網絡模型，由輸入層、輸出層和儲備池層組成.儲備池層由大量隨機相連的神經元構成，將輸入信號映射到更高維度的狀態空間.假設一個ESN的輸入層包含D個單元，儲備池層有N個單元，輸出層有d個單元.若u（t）∈RD，x（t）∈RN，y（t）∈Rd分別表示外界的輸入、儲備池的輸出及整個網絡的輸出，則儲備池層節點的動力學可以表示為

其中Wm∈RNxD，W∈RNxN分別是輸入-儲備池層的權值和儲備池層權值，這些權值隨機產生并且在運行過程中不需要更新.整個ESN網絡的輸出為

這里[·；·]表示縱向串聯.在回歸任務中，f（·）通常為單位函數，W∈Rdx（N+D）可以通過嶺回歸算法計算[2.矩陣W的設計是ESN是否成功的關鍵，其主要受稀疏度和譜半徑rm等參數的影響，其中稀疏度通常為10%～20%，譜半徑通常被歸一化為mlt;1以獲得回聲狀態特性[2]。

Leaky-ESN（L-ESN）是一種改進的ESN模型[5]，儲備池層動力學描述為

L-ESN通過引入參數a∈[0，1]建立系統當前與其上一步狀態之間的關系.

2延遲反饋回聲狀態網絡

本文提出一種具有延遲自反饋效應的ESN模型（delay-ESN），若引入隱層狀態的延遲反饋Yx，-m，則其隱層輸出可表示為

這里f（·）表示隱層節點的激活函數，滿足

且

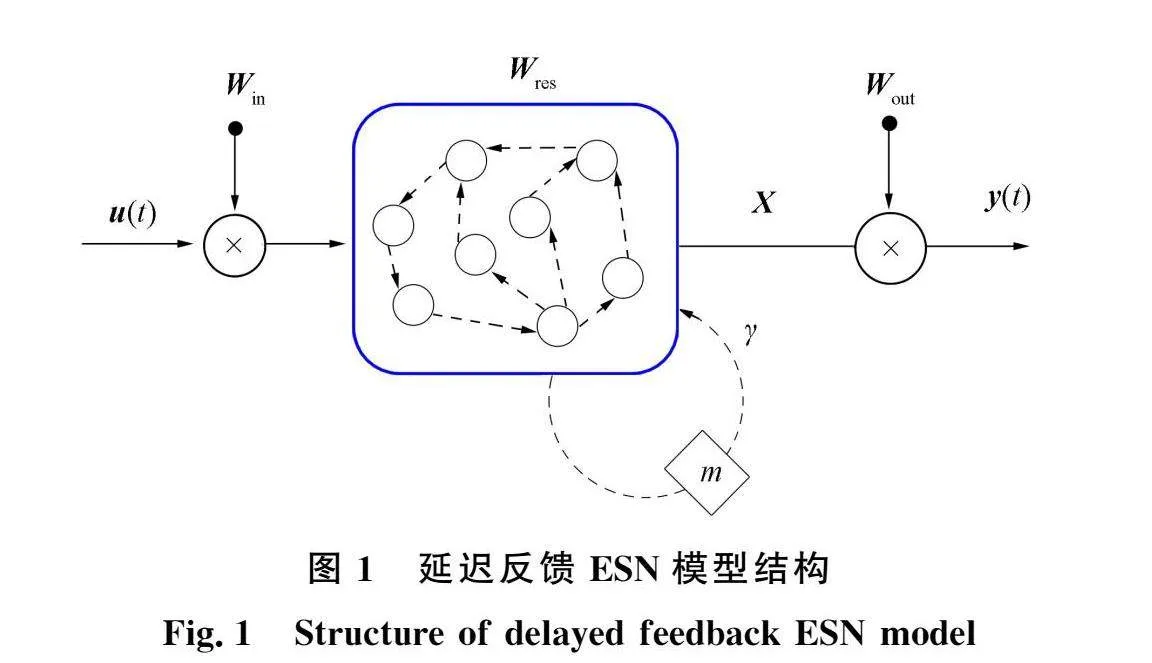
xm表示延遲自反饋，y為反饋強度，m≥0為反饋延遲.延遲自反饋建立了儲備層狀態的當前和先前m時間步之間的關系，提供了反映系統動態特性的有效途徑，其模型結構如圖1所示，其中虛線箭頭表示延遲反饋，m表示m步延遲，y為反饋增益.

在訓練階段，回聲狀態x（t）按列堆登到狀態X中，對應的教師輸出值y（t）按列堆登成向量Y.當輸出單元的激活函數是單位函數時，輸出層變成線性組合器.因此，網絡訓練的目的是通過求解如下優化問題：

找到最優的輸出權值：

這里‖·‖表示Euclid范數，I表示單位矩陣，是正則化參數.

當獲得了最優的權值W后，將網絡的輸出反潰到輸入層作為輸入信號，即令u（）=y（t），則可以對系統的動態行為進行預測，表達式為

delay-ESN具有以下特點：

1）引入延遲反饋可以更好地模擬神經元之間信號的有限傳輸速度和延遲交互作用；

2）通過引入延遲狀態反饋，考慮了系統過去狀態對系統的影響，提高了記憶能力；

3）如果沒有自反饋，則delay-ESN退化為標準ESN；

4）L-ESN只考慮了隱含層與其上一個時刻的狀態的線性組合，而delay-ESN考慮了隱含層與其之前m個時間步的狀態之間的非線性關系，具有更好的動態性能.

3回聲狀態特性分析

ESN模型中最重要的特征是回聲狀態特性（ESP），即驅動的儲備池需要對小擾動具有魯棒性13.當不滿足該條件時，兩個非常接近的輸入信號可能導致兩個非常不同的儲層表示，進而導致ESN對監督學習任務毫無用處.事實上，在擾動或噪聲存在的情況下，沒有ESP的網絡準確性會很差：一個小擾動即可能使網絡達到前所未有的狀態，破壞網絡的預測能力.

假設1非線性激活函數f（u，x，z）在集合D∈RN上滿足局部Lipchitz條件：

這里a和3是已知常數.

定理1如果delay-ESN模型滿足下列條件：

1）f（·）滿足假設1；

2）apmax+B|y|lt;1，這里pmax是矩陣Wres的范數.

則delay-ESN模型具有回聲狀態特性.

證明：設x2和z2分別是不同初始條件下儲備池的輸出狀態，這里x2（0）≠z2（0），則有

因此根據文獻[1，3]的結論，如果滿足條件1）和2），則delay-ESN模型有回聲狀態特性.

4數值實驗

下面通過混沌時間序列預測實驗驗證delay-ESN模型的有效性.實驗中，輸入數據和教師數據都被歸一化為具有均值0和標準差1.儲備池層的節點數設為500，Wm和W中的元素由（-0.5，0.5）內隨機均勻分布的隨機數組成，用均方根誤差（RMSE）衡量模型的性能：

其中y。（t）表示輸出的教師信號，y（t）表示預測值，T為預測的時間步長.

考慮Rossler混沌系統，定義為

其中a=0.15，3=0.2，0=10.則系統展現出混沌特性.

Rossler系統分量的軌跡表現出不規則的跳躍行為，許多ESN方法很難準確預測該系統.選擇初始條件（xo，yo，zo）=（0，1，0），使用Runge-Kutta方法生成6000個數據點的三維時間序列，時間步長為0.01.其中前1000個樣本用于預熱，2500個數據作為訓練儲層的輸入，其余的2500個數據用于測試ESN的預測性能，實驗中參數的設定滿足定理1條件，并且r=0.9，7=0.1，=10-8.

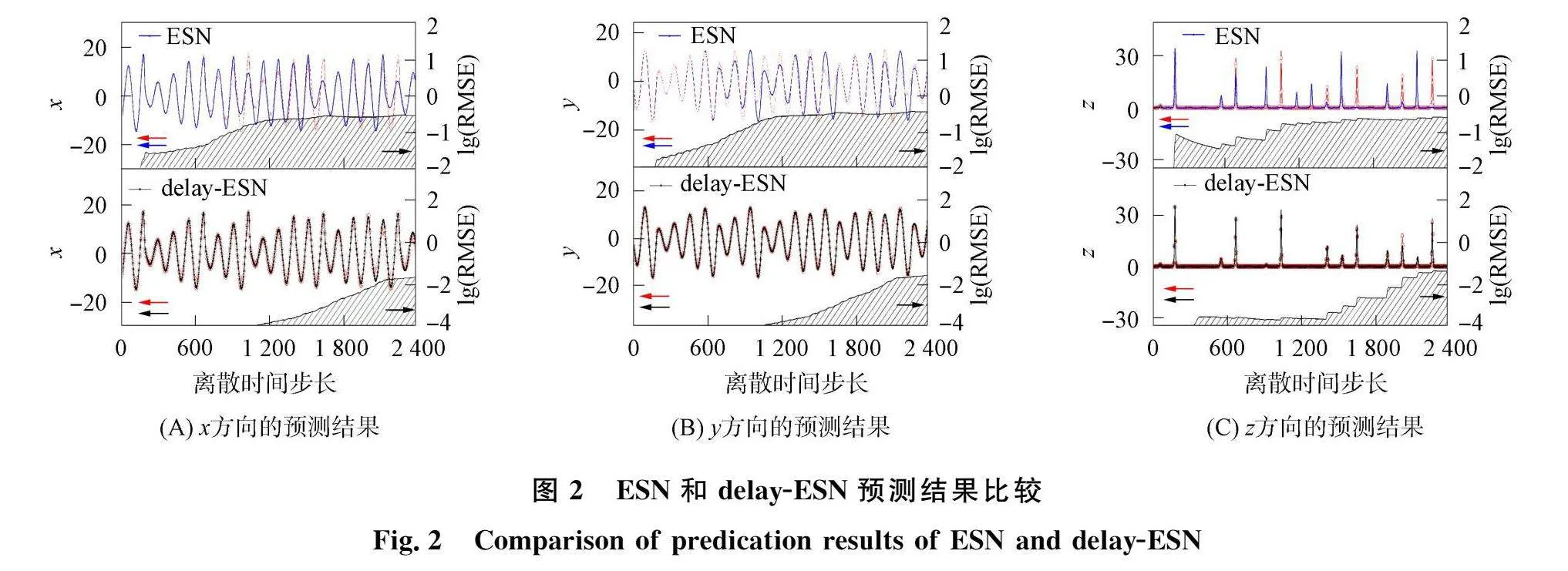
選擇參數y=-0.22，m=6，圖2為delay-ESN和ESN的預測曲線和RMSE，其中陰影部分表示delay-ESN的RMSE.由于Rossler混沌系統對初始值的敏感性，因此由圖2可見，當離散時間步長約小于153時，ESN有較好的預測結構，其中RMSElt;10-2.但隨著時間的延長，ESN的預測逐漸偏離了實際軌跡，當離散時間大于900時，RMSEgt;10-1，預測性能不佳.但當離散時間步長達2000時，delay-ESN的預測軌跡仍可以準確地跟蹤實際的混沌曲線，預測RMSElt;10～2.實驗結果表明，本文提出的delay-ESN可以實現混沌系統的長期預測.

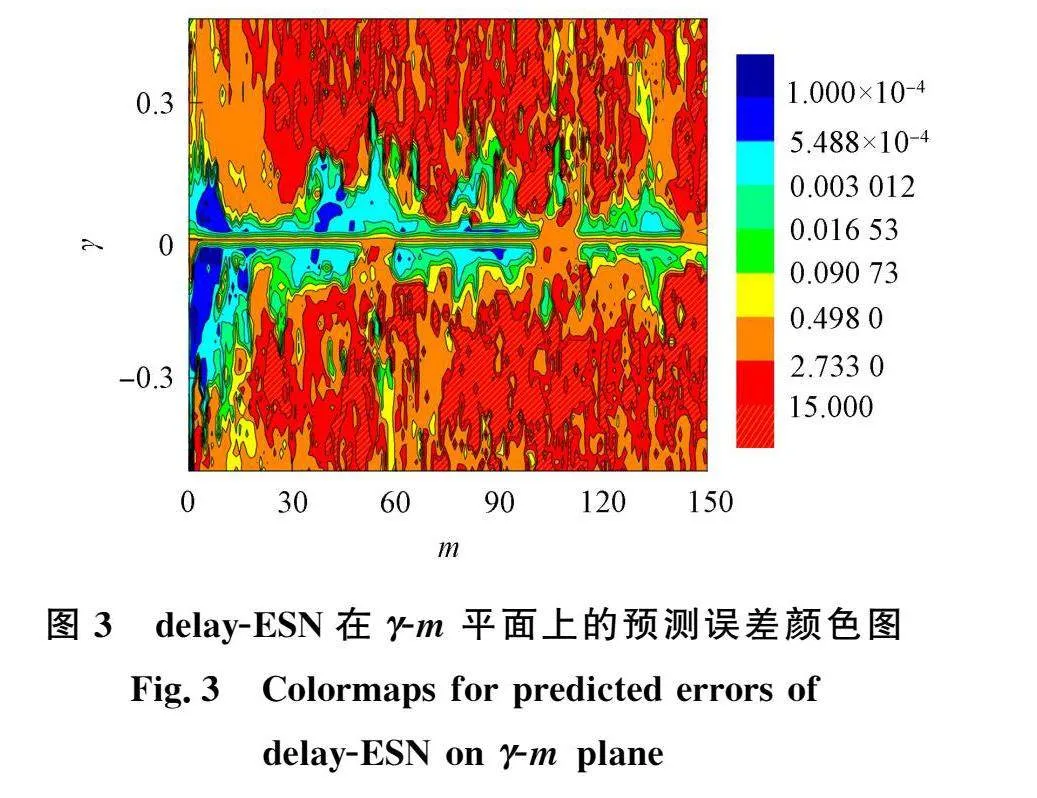
對參數（y，m）進行網絡劃分，在參數的交叉點上計算RMSE，則可以得到RMSE的區域顏色圖，其中顏色深淺表示了RMSE的大小.當參數位于綠色和藍色區域時，預測誤差非常小（RMSElt;0.1）.圖3為delay-ESN在Y-m平面內的預測誤差顏色圖.由圖3可見：

1）delay-ESN 可以在很大的（γ，m）參數范圍內給出更好的預測結果，因此更容易選擇參數γ 和 m，以獲得更好的預測結果，降低了經典 ESN 方法選擇最優參數的困難;

2）與經典 ESN 相比，負反饋增益可實現良好的收斂性，這與許多現有的帶有參數的 ESN 方法 （如LeakyESN）非常不同，這些模型中參數通常是正的;

3）隨著延遲的增加，具有更好預測精度的參數逐漸減小，呈現出近似周期性變化模式;

4）預測精度較高的參數通常位于具有小延遲和小反饋增益的區域，在實際問題中，可以從這些區域搜索參數以獲得更好的精度.

綜上可見，作為一種新型的回歸神經網絡模型，回聲狀態網絡有效克服了傳統RNN建模中遇到的梯度爆炸和梯度消失問題，在混沌時間序列預測中取得了優異的效果.但由于ESN的短期記憶能力，其動態性能略有不足，難以實現復雜系統的長期行為分析和預測。本文考慮了神經元信號有限的傳播速度，將儲備池層神經元的延遲反饋引入到儲備池狀態的更新過程中，提高了傳統ESN方法記憶能力不足的問題，并且對模型的回聲狀態特性進行了分析，給出了確保delay-ESN穩定收斂的充分條件，雖然提出的模型引入了兩個額外參數，但易通過對這些參數的搜索獲得更優的計算性能.數值實驗結果表明，本文提出的方法在混沌時間序列數據的分析和預測中效果很好。本文的數值實驗雖然只與經典的ESN模型進行了對比，但可以在一些改進的模型中引入延遲反饋獲得更好的記憶性能，從而更有利于在實際問題中應用.

參考文獻

[1]JAEGER H，HASS H.HarnessingNonlinearity：Predicting Chaotic Systems and Saving Energy in Wireless Communications[J].Science，2004，304：78-80.

[2]GAUTHIER D J，BOLLT E，GRIFFITH A，etal.Next Generation Reservoir Computing[J].Nature Communications，2021，12：5564-1-5564-7.

[3]GONG Z C，CHEN H H，YUAN B，etal.Multiobjective Learning in the Model Space for Time Series Classification[J].IEEE Transactions on Cybernetics，2019，49（3）：918-932.

[4]BIANCHI F M，SCARDAPANE S，L?KSE S，etal.Reservoir Computing Approaches for Representation and Classification of Multivariate Time Series[J].IEEE Transactions on Neural Networks and Learning Systems，2021，32（5）：2169-2179.

[5]GALLICCHIO C.MICHELI A，PEDRELLI L.Deep Reservoir Computing：A Critical Experimental Analysis[J].Neurocomputing，2017，268：87-99.

[6] GALLICCHIO C，MICHELI A，PEDRELLI L.Design of Deep Echo State Networks[J].Neural Networks，2018，108：33-47.

[7]OTTE S，BUTZ M V.KORYAKIN D.et al.Optimizing Recurrent Reservoirs with Neuro-Evolution[J].Neurocomputing，2016，192：128-138.

[8]QIAO J F，LI F J.HAN H G.et al.Growing Echo-State Network with Multiple Subreservoirs[J].IEEE Transactions on Neural Networks and Learning Systems，2016，28（2）：391-404.

[9]WANG H S，LIU Y X.WANG D S，etal.Discriminative and Regularized Echo State Network for Time Series Classification[J].Pattern Recognition，2022，130：108811-1-108811-14.

[10]ROY M，MANDAL S，HENS C.et al.Model-Free Prediction of Multistability Using Echo State Network[J].Chaos，2022，32（10）：101104-1-101104-8.

[11]PATHAK J，HUNT B，GIRVAN M，etal.Model-Free Prediction of Large Spatiotemporally Chaotic Systems from Data：A Reservoir Computing Approach[J].Physical Review Letters，2018，120（2）：024102-1-024102-5.

[12]ZHANG H，FAN H W，WANG L，etal.Learning Hamiltonian Dynamics with Reservoir Computing[J].Physical Review E，2021，104（2）：024205-1-024205-12.

（責任編輯：趙立芹）